基于改进遗传算法的船舶航向PID控制器

欧阳子路， 余文曌， 贺宏伟， 佘航宇

(武汉理工大学 a. 交通学院； b. 物流工程学院， 武汉 430063)

基于改进遗传算法的船舶航向PID控制器

欧阳子路a， 余文曌a， 贺宏伟a， 佘航宇b

(武汉理工大学 a. 交通学院； b. 物流工程学院， 武汉 430063)

为提高遗传算法对船舶航向PID控制器控制参数整定的效果，提出一种改进的遗传算法，设计自适应交叉算子和变异算子，动态调整交叉概率和变异概率。同时，针对船舶操舵转艏模型，设计恰当的目标函数和超调惩罚机制。仿真试验结果表明，该航向控制器具有收敛速度快、没有超调等优点。

船舶工程；PID；遗传算法；自适应函数；目标函数

Abstract: An improved genetic algorithm for adjusting the parameters of the ship heading PID controller is proposed. The adaptive crossover operator and mutation operator are designed to change the crossover probability and mutation probability dynamically. The objective function and punishment mechanism for overshoot are also developed based on steering-turning model. Simulation experiment results show that the control system is characterized by fast convergence without overshooting.

Keywords: ship engineering; PID； genetic algorithm; adaptive function; objective function

在船舶姿态控制中，航向控制是十分重要的环节。就现有的船舶而言，大部分船舶采用PID(Proportion Integral Derivative)控制自动舵，随之出现多种PID控制优化算法应用到船舶航向控制中，提高了PID控制自动舵的控制性能。

遗传算法具有并行性，能用较少的代码串完成较大范围的搜索[1],因此适于解决复杂的控制系统问题。若结合PID控制器对比例、微分及积分参数进行动态优化调整，则能在一定程度上增强自动舵的控制性能。然而，采用基本遗传算法对PID参数进行优化，存在收敛速度慢、产生超调和稳态误差大等一些不可忽视的问题，因此采用传统遗传算法整定船舶航向PID控制器参数已不能满足当前对船舶控制性能和系统鲁棒性的要求。

针对该情况，在传统遗传算法的基础上提出自适应交叉概率和变异概率的函数，同时针对船舶操舵转艏模型设置合适的目标函数，以提高航向控制器的收敛速度并消除超调，大幅度提高船舶航向PID控制器的性能。

1 船舶运动数学模型及航向PID控制

1.1船舶运动数学模型

若考虑船舶的横漂速度v和转艏角速度r，则可得到操舵对艏摇响应的方程，其传递函数为

(1)

野本谦作等依据船舶自身巨大的惯性对船舶操纵运动线性方程线性进行简化。[2]对于惯性较大的船舶，其自身的动态特性在低频段更加重要，令拉普拉斯算子s=jw趋近于0，同时忽略二阶小量和三阶小量，推导出船舶运动控制领域常用的野本模型为

(2)

式(2)中：K1为船舶的回转性指数；T1为船舶应舵指数；s为拉普拉斯算子。

1.2航向PID控制

传统PID自动舵原理见图1。船舶在实际航行时会受到风、浪、流的作用，其实际的航向会与预设的航向产生稳态误差，在传统PID自动舵系统中，期望航向值r(t)与实际航向值y(t)的差值e(t)构成航向偏差，经过比例、积分及微分运算得到航向角实际输出u(t)为

(3)

式(3)中：Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

2 改进遗传算法PID航向控制器设计

利用遗传算法对航向PID控制器的3个关键参数Kp,Ti,Td进行整定。简单遗传算法的数学模型[3-4]可表示为

ASG=(M,F,P0,G,Φ,Ι,Ψ,T)

(4)

式(4)中：M为参数的编码方法；F为评价个体好坏的适应度；P0为初始种群；G为种群规模；Φ为选择算子；Ι为交叉算子；Ψ为变异算子；T为算法终止的条件。

简单遗传算法本身存在一定的问题，例如局部搜索能力差，存在未成熟和随机游走等现象，导致算法的收敛性较差，需花费很长时间才能找到最优解[5]，若将其应用到PID船舶航向控制器上，则会出现频繁操舵的现象，增大工作强度；同时，若选取不适当的目标函数，则航向控制器的超调和振荡现象将无法得到有效控制。因此，设计基于改进遗传算法的船舶航向PID控制器，着重设计自适应的交叉算子和变异算子，并根据船舶操舵转艏模型的特殊性设计恰当的目标函数及超调惩罚机制。

2.1编码

采用遗传算法中最常用的二进制编码对需要寻优的控制参数Kp,Ti,Td进行编码，其编码符号集为二值符号集{0,1}，个体基因为二值符号串。用长度为L的二进制编码串分别将Kp,Ti,Td离散，3个二进制码串组成的3L位二进制数将成为一个基因型，表示一个可行解。可行解的形式为

2.2种群初始化

采用计算机随机产生离散化的Kp,Ti,Td初始种群，产生0～1.0内均匀分布的随机数，规定产生的随机数在0～0.5内代表0，在0.5～1.0内代表1，种群大小为n。

2.3选择算子

采用轮盘赌选择法，类似于博彩游戏中的轮盘赌，个体适应度按比例转换为选择概率，按个体所占的比例在圆盘上进行比例划分，每次圆盘转动停止后指针停靠扇区对应的个体即为选中的个体。[6]

2.4自适应交叉算子和变异算子设计

交叉操作[7]类似于自然界中生物进化时的基因重组；变异操作[8]用来模拟自然界中生物繁殖时产生的基因突变，被认为是产生新个体必不可少的辅助方法。

基本遗传算法的交叉概率和变异概率均为定值，由模式定理可知，具有低阶、短定义距特性及平均适应度高于种群平均适应度的模式在子代中呈指数增长。[9]因此，在寻优初期，模式将集中在适应度值较小的个体上，此时若采用较小的交叉概率和变异概率，将难以产生新的优秀子代，使收敛速度减慢，表现在船舶航向PID控制上会使实际航向长时间达不到期望航向，影响控制器的性能；在寻优后期，模式将集中在适应度值较高的个体上，此时若采用较大的交叉概率和变异概率，将会破坏优良的个体基因型，陷入到局部收敛的局面中，表现在船舶航向PID控制上会造成频繁操舵，影响舵机的机械性能并导致能源浪费。

针对以上问题，设计一种自适应交叉算子和变异算子，即

(5)

(6)

式(5)和式(6)中：i为进化代数；P1为交叉概率初值；P2为变异概率初值；n为样本个数；k1和k2为权值，可根据具体船舶操舵转艏模型调节。式(5)和式(6)建立了交叉概率和变异概率与进化代数和种群大小的关系。

1)i作为自变量，使交叉概率和变异概率随着进化代数的增加而线性递减，有利于增强控制器在寻优前期产生新基因型个体的能力及在寻优后期保留优秀个体的能力。

2)n作为调节因子，使交叉概率和变异概率的递减速率随着种群大小的变化而变化：当种群数目较多时，交叉概率和变异概率的递减速率会放缓，目的是保证每代Pc和Pm都适宜，获得良好的动态性能。

2.5目标函数设计

目标函数的值是遗传算法评价个体好坏的依据，因此目标函数的选取直接影响到遗传算法的收敛速度及能否找到最优解。[10]考虑到船舶航向控制的实际情况，为获取满意的操舵转艏过程动态特性，目标函数由2部分组成(见式(7))，其中：

1)第1项采用航向角误差绝对值时间积分性能指标,目的是获得更高的航向控制精度。

2)第2项采用航向角实际输出的平方时间积分性能指标，目的是防止获得的航向角输出过大，降低工作强度，使船舶航向平缓地趋近于期望值。

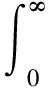
y(i)-y(i-1)>0

(7)

式(7)中：y(i)为第i个进化代数下的实际航向值；w1和w2为权值，可根据实际控制目标选取。

此外，为消除超调对自动舵系统控制效果的影响，设计超调惩罚式(见式(8))，并在式(7)的基础上引入船舶实际航向值前后时刻差值的绝对值时间积分性能指标，当船舶后一时刻的实际航向值小于前一时刻的航向值时，该群体集将得到数值较大的函数值，遗传算法寻优进程即跳入到惩罚环节。

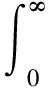
y(i)-y(i-1)<0

(8)

改进遗传算法整体实现流程见图2。

3 仿真结果与分析

选择野本模型，以上海大学机电工程自动化学院和北船重工联合研制的无人艇为研究对象，船舶主要参数[11]为：船长6.5 m；船宽3.2 m；满载吃水0.8 m；T=2.88；K=0.855。

设计传统遗传算法PID自动舵和改进遗传算法PID自动舵2种自动舵。传统遗传算法中的交叉概率取0.9，变异概率取0.1。对于改进遗传算法中的自适应交叉算子和变异算子，交叉概率初值P1取0.9，变异概率初值P2取0.1，权值k1和k2均取0.01；在目标函数中，权值w1取0.999，w2取0.001，w3取1 000；二进制编码串长度L均取10，种群大小n均取30，进化代数均取100代，船舶初始航向均定为000°，期望航向改变量均定为+10°。

图3和图4反映期望航向角变化+10°时2种自动舵实际航向与性能指标的仿真变化，从图中可看出：相比传统遗传算法PID自动舵，改进的自动舵收敛速度更快、航向更快得到稳定，且振荡幅度小、没有超调。收敛速度更快、系统较快得到稳定可归因于自适应交叉算子和变异算子的设计，而没有超调和振荡幅度较小可归因于符合船舶操舵转艏模型的目标函数的设计。

4 结束语

本文研究PID控制、遗传算法及船舶操舵转艏模型，着重对遗传算法的传统交叉算子、变异算子及目标函数的设计进行改进，并对船舶航向PID控制器进行离线优化与仿真，得到以下结论：

(1)根据船舶操舵转艏运动模型的特点设计恰当的目标函数，并设计自适应交叉算子和变异算子，使交叉概率和变异概率随着遗传代数的变化而变化;

(2)仿真结果表明，本文设计的基于改进遗传算法的PID自动舵相比传统的PID自动舵具有收敛速度更快、没有超调和振荡幅度较小等优点。

[1] 何佳佳,侯再恩.PID参数优化算法[J].化工自动化及仪表,2010,37(11):1-4.

[2] NOMOTO K, TAGUCHI K, HONDA K, et al. On the Steering Qualities of Ships[J]. International Shipbuilding Progress, 1957,4(35):354-370.

[3] 成学亮,尉宇,王涛.基于改进遗传算法的PID参数寻优与控制器设计[J].计算机与数字工程, 2009,37(3):78-81.

[4] FANG MC, LIN YH, WANG BJ. Applying the PD Controller on the Roll Reduction and Track Keeping for the Ship Advancing Waves[J]. Ocean Engineering,2012,54(4):13-25.

[5] 葛继科，邱玉辉，吴春明，等.遗传算法研究综述[J].计算机应用研究，2008,25(10):2911-2915.

[6] 白峻尧,杨世兴,石玉芳,等.基于轮盘赌的图像传输技术研究与应用[J].仪表仪器用户,2006,13(3):47-48.

[7] MANIEZZO V. Genetic Evolution of the Topology and Weight Distribution of the Neural Networks[J]. IEEE Transactions on Neural Networks,1994,5(1):39-53.

[8] MÜHLENBEIN H. How Genetic Algorithms Really Work: Mutation and Hill Climbing[C]. Parellel Problem Solving from Nature 2,1992:15-25.

[9] GOLDBERG DE. Genetic Algorithm in Search Optimization and Machine Learning[M].Boston:Addison-Wesley,1989.

[10] 张思才,张方晓.一种遗传算法适应度函数的改进方法[J].计算机应用与软件,2006,23(2):108-110.

[11] 彭艳,吴伟清,刘梅,等.无人艇航迹跟踪GPC-PID串级控制[J].控制工程，2014,21(2):245-248.

PIDControlwithImprovedGeneticAlgorithmforShipSteering

OUYANGZilua,YUWenzhaoa,HEHongweia,SHEHangyub

(a. School of Transportation; b.School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China)

余文曌(1989—)，男，湖北武汉人，讲师，从事智能船舶航行技术、无人艇容错控制技术、船舶动力定位系统智能控制算法及系统设计研究。E-mail: wzyu@whut.edu.cn

U664.82；TP273.5

A

2016-12-25

中央高校基本科研业务费专项资金(163102006)；武汉理工大学国家级大学生创新创业训练计划(20161049702003)

欧阳子路 (1996—), 男, 湖北武汉人，本科，从事智能船舶航行技术研究。E-mail: 2490934562@qq.com

1000-4653(2017)01-0013-03