变压器计及局部安匝不平衡时的轴向动态响应

荣佳星 刘文里 牛一博 李祎春 唐宇

摘要：基于電磁学及力学理论，运用MagNet仿真软件，针对一台120MVA/220kV无励磁调压变压器，建立短路工况下计及安匝不平衡的三维模型，计算绕组线饼所受到的轴向电动力。可以发现绕组受局部安匝不平衡的影响，轴向电动力会在调压绕组端口处产生较大的跃变，且最大轴向电动力出现的位置不再是绕组端部，而在调压绕组端口处。再运用ANSYS软件建立“弹簧-质量-阻尼”模型分析绕组的轴向动态响应，会发现由于最大轴向电动力出现的位置的变化，垫块的最大承受力位置也在变化，最大承受力为112MPa，在许用应力范围内。通过对振动位移的分析可以得到相应变化规律，再通过频谱分析确定绕组固有频率对动态响应的影响，最后对绕组的机械应力及稳定性进行分析。

关键词：变压器；短路工况；安匝不平衡；轴向电动力；动态响应

DOI：1015938/jjhust201705010

中图分类号： TM411

文献标志码： A

文章编号： 1007-2683（2017）05-0052-06

收稿日期： 2016-03-16

作者简介：

刘文里（1956—），男，教授，硕士研究生导师；

牛一博（1990—），男，硕士研究生

通信作者：

荣佳星（1991—），男，硕士研究生，Email：18724608322@163.com

Axial Dynamic Response Analysis of Transformer

with Local Unbalancedampere Turns

RONG Jiaxing1，LIU Wenli2，NIU Yibo3，LI Yichun4，TANG Yu5

（1State Grid Jiamusi Power Supply Company，Jiamusi 154002，China；

2School of Electrical and Electronic Engineering，Harbin University of Science and Technology，Harbin 150080，China；

3School of Information Science and Engineering，Jishou University，Jishou 416000，China；

4Materials Company of State Grid East Inner Mongolia Electric Power Company Limited，Hohhot 010020，China； 5Overhauling Company of State Grid Heilongjiang Electric Power Company Limited，Harbin 150090，China）

Abstract：Based on the theory of electromagnetism and the mechanics theory，it uses the finite element simulation software named MagNet to establish threedimensional model considered unbalanced ampere turns to calculate the shortcircuit electromagnetic force for a 120MVA/220kV without excitation transformer and then get the analysis of axial electric line cakeIt can be found by local ampereturns imbalance， the influence of axial port in regulating winding electric will produce larger distortionAnd the position of maximum axial electric appeared no longer is winding ends， but in regulating winding portThen it analyzes the axial dynamic response by establishing the "Springqualitydamping” model We will find that due to the change of the location of the maximum axial electric appeared， the maximum tolerance block position is changing and the maximum pressure is 112MPa We can get the corresponding variation law by the analysis of vibration displacement Then determined by winding inherent frequency spectrum analysis of the influence of dynamic response Finally， the mechanical stress and stability of the winding is analyzed

Keywords：Transformer； Short circuit conditions； Ampere turns unbalance； The axial electric force； Dynamic responseendprint

0引言

轴向稳定性是变压器的重要指标之一[1-2]。随着对变压器轴向稳定的要求越来越高，以往的二维模型由于缺少铁心、油箱等不同磁导率的导磁结构的考虑，已经逐渐无法满足轴向稳定性分析精度要求了[3-8]。本文针对一台120MVA/220kV无励磁调压变压器，通过MagNet软件建立计及安匝不平衡、非线性铁心和油箱材料的三维模型，得到绕组最小分接下高压绕组的轴向电动力，可以得到受局部安匝不平衡而产生影响的轴向电动力的受力最大线饼，再通过ANSYS软件依照实际尺寸建立“弹簧-质量-阻尼”模型，对高压绕组的轴向动态响应进行分析，通过对绕组线饼之间垫块所受压缩压强的大小进行分析，可以看出在其最大受压位置的变化与绕组的最大轴向短路力受力线饼位置有关，并根据振动系统的变化位移来找出其振动规律，最后通过频谱分析可以得到绕组固有频率对振动响应的影响。

1计算原理

11场路耦合原理

在磁场分析中，可以利用场路耦合的方式来进行计算，根据电路参数的变化可以计算设备不同运行情况的电磁特性[9-10]。如图1所示，把整个有限元区域当做电路中的元件接入等效电路中。在短路工况下，左侧绕组线饼对应变压器高压绕组，并施加额定相电压；右侧对应低压绕组，并将负载阻抗视为零[11-12]。

12动态响应计算原理

分析轴向动态响应时，可以将绕组各个线饼视为集中质量，绝缘垫块和端圈视为弹性元件，在轴向力作用下的绕组可以等效成由若干集中参数构成的“质量-弹簧-阻尼”轴向振动模型[13-15]，如图2所示。

对于图2的多自由度振动系统，根据弹性动力学理论，各质量单元运动方程为[16-20]

M+C+KZ=F（t）+Mg（4）

式中：Z为各线饼绝对位移，Z=z1 z2 … znT；F为各线饼轴向短路电磁力，F=f1 f2 … fnT；M为系统的质量矩阵，M=diagmii=1，…，n；C为系统的阻尼矩阵，C=trid[cij]，cii=ci-1+ci，ci，i+1=ci+1，i=-ci（i=1，…，n）；K为系统刚度矩阵，K=trid[kij]，kii=ki-1+ki，ki+1，i=-ki（i=1，…，n）。

绝缘纸板的应力-应变关系在一定范围内可以表示为

σ=aε+bε3（5）

式中：σ为应力；ε为应变；a=105MPa；b=17500MPa。

则弹性模量为

E=dσdε=a+3bε2（6）

对应的等效刚度系数为

K=E·Ah（7）

式中：A为绝缘垫块（端圈）与线饼相接触总面积；h表示绝缘垫块（端圈）高度。

對大型变压器阻尼比约为ξ=009[21]，则粘性阻尼系数可表示为

C=2ξKM（8）

2实例计算

21基本参数

本文针对一台120MVA/220kV无励磁调压变压器，运用MagNet软件，建立了短路工况下的“场-路耦合”模型，模型变压器主要参数如表1、2所示。

22模型建立

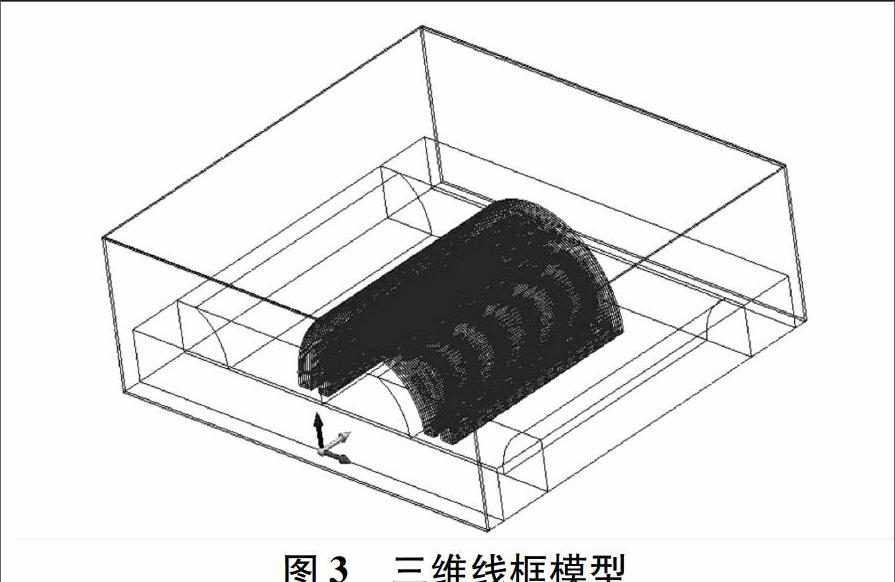
在分析的过程中，基于变压器磁路特点，可假设忽略其相间影响、导线涡流作用等影响。利用MagNet仿真软件建立包括铁心、油箱壁、箱盖、箱底、铁轭、绕组及油在内的三维模型。线框模型如图3所示。

23仿真模型的验证

电力变压器最小分接下短路阻抗实测值与“场-路耦合”方法的计算值分别是1401%和1398%，偏差值约为021%。由此得出“场-路耦合”法计算的短路阻抗值与实测值相比较有较小的偏差，说明在MagNet仿真软件中，采用考虑安匝不平衡建立有限元三维仿真模型及计算方法对该变压器是适用的。

24轴向短路电动力的计算

通过MagNet软件瞬态三维求解，可以得到所建模型在电压初相角α=0，即短路后的t=001s时刻，最小分接下漏磁感应强度的分布云图，如图4所示。

由图4可以看出，在最小分接下，调压绕组线段并没有接入高压绕组中，使得模型中的高压段中间两处分别存在4饼线饼没有电流，因此在其相对应的位置出现了较为严重的局部安匝不平衡现象，其主空道中的漏磁感应强度相对其他位置也有所减弱。

图5为变压器绕组的辐向漏磁场的分布示意图，由图中可以看出在调压绕组线段端口处，出现了较强的辐向漏磁场的急剧变化，这就会导致轴向电动力在此位置发生突变。

由图6可以看出，最小分接下高压轴向电动力随线饼号变化曲线极不平滑，甚至在绕组出现力在方向上的波动，并且在调压绕组线段端口处发生跃变，形成了最大的轴向电动力。

25轴向动态响应分析

运用ANSYS软件，以高压绕组实际结构建立“质量-弹簧-阻尼”模型，分析轴向压紧预应力为3MPa时最小分接下高压绕组的动态响应问题。

从表3中可以看出，在轴向压紧预应力为3MPa时高压绕组在100Hz内有32Hz与72Hz两个固有频率，符合“大容量变压器绕组具有多个固有频率，且有可能在100Hz以内”的研究结果[6]。

由图7可以看出，模型上端部所受最大向上的压力为213963N，如此大的作用力主要是由于绕组安匝的不平衡分布所导致的。由于垫块的面积为008136m2，所以上压板所受到的压强为263MPa，小于轴向压紧预应力3MPa。

综合考虑指向绕组中间的轴向压缩力，以及由于安匝不平衡分布引发的指向上下铁轭的力发现，由于最大的轴向电动力的位置受局部安匝不平衡影响而导致其位置变化，不再是端部，导致承受最大压缩压强的垫块也不再是中间垫块。由图8可见，在“质量-弹簧-阻尼”模型中，第21号垫块所受到的压缩压强要大于56号垫块，且在t=001s时达到最大值为82MPa。垫块所受的总压强还要考虑轴向压紧预应力，所以垫块实际所受的最大压强为112MPa，小于许用应力35MPa，不会造成垫块的破坏。endprint

在时间为t=001s时，线饼号的振动位移分布如图9，此时在绕组17、56、98号线饼附近振动位移接近为0mm，在77号线饼处达到最大位移32mm。由于41到44号线饼、69到72号线饼没有电动力的作用，只能依靠其他单元的力带动，所以系统没达到稳定之前，其对应位置曲线斜率变化较大。绕组位移分布在t=001s时，上下线段相对于图6中的高压绕组的轴向短路电动力来说，绕组上下的不对称情况较为明显，这是力的累积效应体现在位移上形成了较大的差异，而且此种差异会随着振动时间的推移越来越大，最终形成上下不对称程度很大的位移分布。如图10所示，在t=02s时刻，1号线饼的位移是0511mm，112号线饼的位移是0277mm，下面的绕组线段振动幅度明显大于上面的绕组线段，绕组位移分布上下已经基本不对称。

26线饼位移的频谱分析

图11和图12分别是第40号绕组线饼的振动位移曲线和频谱。在频谱分析中，由于振动系统中的阻尼作用，导致频谱中的尖端左右斜率偏移较大，通过图12可以看出，绕组固有频率32Hz、72Hz、119Hz，避开了变压器短路工况下幅值极值点50Hz、100Hz[6]，使得位移振动频谱中在15Hz、35Hz、66Hz、86Hz、118Hz达到极值，这就是绕组的固有频率对轴向振动产生影响的效果。

27绕组的机械应力校核

依据机械应力的校核公式[6]，可以得到校核结果如表4所示。

如表4所示，可以看出高压绕组上的机械应力都在许用应力范围内，且安全裕度充足，绕组的机械应力符合校核标准，不会出现永久变形等现象。

28绕组的稳定性校核

对变压器的高压绕组进行轴向失稳校核，可以得到高压绕组的轴向临界力为2104kN，其最大漏磁段的轴向合力出现在21～40号线饼，其轴向合力为1279kN，小于轴向临界力，安全裕度为165。由此可以看出，此台变压器的轴向不会出现失稳坍塌现象。

3结论

通过MagNet进行三维瞬态仿真和利用ANSYS软件模型仿真，分别对变压器绕组的磁场和绕组的轴向动态响应进行分析，得到如下结论：

1）由于安匝不平衡分布的影响，导致辐向漏磁场在调压绕组端口处产生较明显变化，使得轴向电动力在其对应位置产生了跃变，且其力的大小超过了端部的轴向电动力。

2）受轴向电动力变化影响，承受压强最大的垫块是21号垫块而非中间垫块，垫块所受最大压强为112MPa，在许用应力35MPa范围内。

3）绕组上下位移分布的不对称情况是力的累积效应在位移上的形成差异的体现，而且此种差异会随着振动时间的推移越来越大。

4）对绕组的机械应力及轴向稳定性进行校核可以得到其安全裕度均符合要求，不会出现永久变形或失稳坍塌等现象。

参 考 文 献：

[1]路长柏电力变压器理论与计算[M].沈阳：辽宁科学技术出版社，2007：178-280

[2]刘文里，李祎春，李赢，等.电力变压器高压绕组辐向稳定性评估[J].哈尔滨理工大学学报，2016，21（4）：90-95.

[3]姜益民变压器运行中短路损坏的常见部位及原因分析[J].变压器，2005，42（4）：35

[4]刘晓丽，刘文里，王明基于“场-路”耦合法的电缆变压器轴向短路电磁力的计算[J].黑龙江电力，2008，30（1）：7-10

[5]李祎春，刘文里，李军，等.大型电力变压器低压绕组辐向稳定性的仿真研究[J].变压器，2016，53（4）：25-29.

[6]GB 10945-2008，电力变压器 第五部分：承受短路的能力[S].

[7]于怀金，刘文里，王录亮电力变压器绕组轴向短路力的研究[J].黑龙江电力，2011，33（4）：260-264

[8]王录亮电力变压器绕组短路力计算[D].哈尔滨：哈尔滨理工大学，2012

[9]LI Yan，ZHOU Wei，JING Yongteng，et alAxial Vibration Analysis of Power Transformer Active Part under Shortcircuit[J].ICEMS，2011：1-4

[10]洪凯星，潘再平，黄海电力变压器绕组轴向振动的建模与分析[J].变压器，2010，47（12）：32-36

[11]李洪奎大型电力变压器绕组短路强度与稳定性研究[D].沈阳：沈阳工业大学，2011

[12]洛君婷，谢德馨，李晓峰，等变压器绕组导线对抗短路能力的影响[J].变压器，201047（5）：16-18

[13]WANG Shishan，LIU Zeyuan，LI Yanming，et alCalculation of Shortcircuit Mechanical Strength for Power Transformer[J].Power System Tecnology，2006，9（6）：1-6

[14]王录亮，刘文里，于会凤电力变压器绕组轴向短路动态力的计算第七届全国变压器技术自主创新研讨会，长沙，2011：59-62

[15]MENG Zhiqiang， WANG ZhongdongThe Analysis of Mechanical Strength of HVWinding Using Finite Element Method，Part Ⅱ mechanical stress and deformation analysis[J].UPEC，2004，1：183-187

[16]辛朝輝，钟俊涛，傅铁军，等大容量变压器内绕组短路强度研究[J].变压器，2009，46（8）：39-42

[17]LIANG Zhengguang，LI Jishun，TANG RenyuanAxial Vibrations of Transformer Windings under Short Circuit Conditions[J].ICEMS，2003：332-335

[18]于怀金大型变压器漏磁场及短路电动力的计算与分析[D].哈尔滨：哈尔滨理工大学，2011.

[19]王世山，汲胜昌，刘家其，等电缆绕组变压器轴向振动模态特性的分析研究[J].电工技术学报，2004，19（10）：6-11

[20]朱维璐，贾永红，杜深慧电力变压器绕组短路轴向稳定性分析[J].变压器，2009，46（9）：17-19

[21]谢毓城电力变压器手册[M].北京：机械工业出版社，2003：142-190

（编辑：关毅）endprint