无死区效应的TNPC型三电平SVG

李文娟++邸金霖++冯杰

摘要：为了降低静止无功发生器SVG的导通损耗，在SVG中引入TNPC型三电平主电路，构建了TNPC型三电平SVG的总体方案。在分析TNPC型三电平主电路工作状态和死区效应的基础上，提出了无死区效应的三载波层叠PWM控制策略。该方法采用上、下两层载波，每层载波均包含原载波、相位超前和相位滞后载波，超前与滞后的相位与死区时间有关。推导了在不同工作状态各功率开关器件的驱动信号和调制波与三载波比较所得信号的逻辑关系。建立了TNPC型三电平SVG仿真模型，搭建了相应实验平台，仿真与实验结果表明该方法在补偿后电网电流电压同相位，功率因数提高，证明了该方法的有效性和正确性。表明引入无死区效应的TNPC型三电平SVG具有更好的无功补偿能力，同时避免了死区效应带给SVG的不利影响。

关键词：

静止无功发生器；三电平；三波层叠PWM；无死区效应

DOI：10.15938/j.jhust.2017.05.009

中图分类号： TM46

文献标志码： A

文章编号： 1007-2683（2017）05-0046-06

Threelevel Static VarGenerator by TNPC Type With No Deadzone Effect

LI Wenjuan，DI Jinlin，FENG Jie

（School of Electric and Electronic Engineering，Harbin University of Science and Technology，Harbin 150080，China）

Abstract：In order to reduce the turnon loss of SVG， the TNPCtype threelevel main circuit is introduced into the SVG， and the overall scheme of the TNPCtype threelevel SVG is constructed. On the basis of analyzing the working state and dead zone effect of TNPCtype threelevel main circuit， a three carrier disposition PWM control strategy without dead zone effect is proposed. The proposed method uses the upper and lower carrier waves， each carrier contains primary carrier， phase lead and phase lag carrier， and the phase of lead and lag is related to deadtime. In this paper， the logic relations between the driving signal of each power switch device and the signal acquired by the modulation wave compared with the three carriers in different working conditions are inferred. The TNPCtype threelevel SVG simulation model is established， and the corresponding experimental platform is built. The simulation and experimental results show that the proposed method can make the current and voltage of the grid same phase and the power factor is increased after compensation， and the validity and correctness of the method are proved. It is shown that the TNPCtype threelevel SVG with no dead zone effect has better reactive power compensation capability and avoids the adverse effect of dead zone effect on SVG.

Keywords：Static Var Generator； threelevel； three carrier disposition PWM； no dead zone effect

收稿日期： 2017-06-27

基金項目： 黑龙江省自然科学基金 （E201444）.

作者简介：

李文娟（1968—），女，教授，硕士研究生导师，Email：liwenjuan@hrbust.edu.cn；

邸金霖（1988—），男，硕士研究生；

冯杰（1991—），女，硕士研究生.

0引言

电力电子设备的广泛应用，在电网中产生大量的无功和谐波，严重影响了电网的安全与高效运行，静止无功发生器（static var generator，SVG）作为一种补偿无功和谐波的新型电力电子装置得到了广泛研究。其中三电平SVG因具有输出电流谐波含量低，直流侧电压利用率高等优点而成为当今的研究重点。三电平SVG核心部件是一个三电平逆变电路，传统的三电平逆变电路主要有二极管中点箝位式、飞跨电容箝位式和混合箝位式，而 TNPC（Ttype neutral point clamped）型三电平逆变电路比传统的三电平逆变电路节省了更多的驱动电源，它利用反向串联的两个功率开关器件来实现直流侧中点箝位功能。较传统三电平逆变电路具有导通损耗低、总谐波失真小及电压利用率高等优点[1-2]，因此TNPC型逆变电路势必成为三电平逆变电路的主流装置。endprint

在三相逆变电路中，为了防止开关器件发生“直通”现象，在同一桥臂的两个开关器件开通与关断之间必须设置一定的死区时间。而死区的加入会引起逆变电路输出电流谐波含量增加、直流电压利用率下降、电压相位出现偏差等死区效应问题[3-8]，进而会影响SVG的补偿性能。

有效解决死区效应的方法主要有两种，一种是通过检测误差电压及死区时间，对电压及时间进行有效补偿，一种是通过调整驱动信号抑制产生死区效应。文[9]采用附加电路的方法解决死区效应，导致逆变主电路结构复杂。文[10]利用功率因数角对电流方向进行间接检测，再对死区效应进行补偿，不利于实际应用。文[11]在级联SVG中，通过直接缩短或延长开关器件的占空比来补偿死区效应，建立模型复杂且计算量大。文[12]采用多载波脉宽调制技术实现无死区控制以解决死区效应对两电平逆变电路的影响，但无法应用到三电平逆变电路中。本文针对TNPC型三电平SVG，在分析主电路工作过程和死区效应的基础上，提出了一种无死区效应的三载波层叠PWM调制法，通过仿真和实验验证了所提方案及方法的有效性。

1总体方案设计及主电路分析

1.1总体设计

TPNC型三电平SVG的控制可分为电流内环和电压外环两部分，电流内环负责无功电流跟踪控制，电压外环保证直流侧电压稳定，由此控制思想确定了如图1所示的总体方案。在图中，uA 、uB 、uC为TNPC型三电平SVG主电路三相交流相电压；iA、iB、iC 为主电路输出的电流，C1 、C2為直流侧的两个电容，Udc为直流侧母线电压；iqref为无功电流参考值，iq是SVG交流侧输出的补偿电流变换后的无功电流分量，需要iq通过PI调节器跟踪iqref；Udcref为直流侧电压参考值，通过计算直接给出，让检测到的实际直流侧电压Udc通过PI调节器跟踪参考值Udcref，同时两者差值经过PI后得到有功电流参考值ipref；id是SVG交流侧输出的补偿电流dq变换后的有功电流分量，使id跟踪有功电流参考值ipref。然后通过dq反变换，得到三相电流信号，并作为PWM调制法的调制波与三重三角载波比较，生成提前关断、滞后导通的开关信号，再通过不同工作状态对开关信号进行逻辑运算，最终得到无死区效应的驱动信号，其中工作状态要根据SVG交流侧瞬时电压电流极性得到，最后送入到TPNC型主电路中控制相应的功率器件。

1.2主电路分析

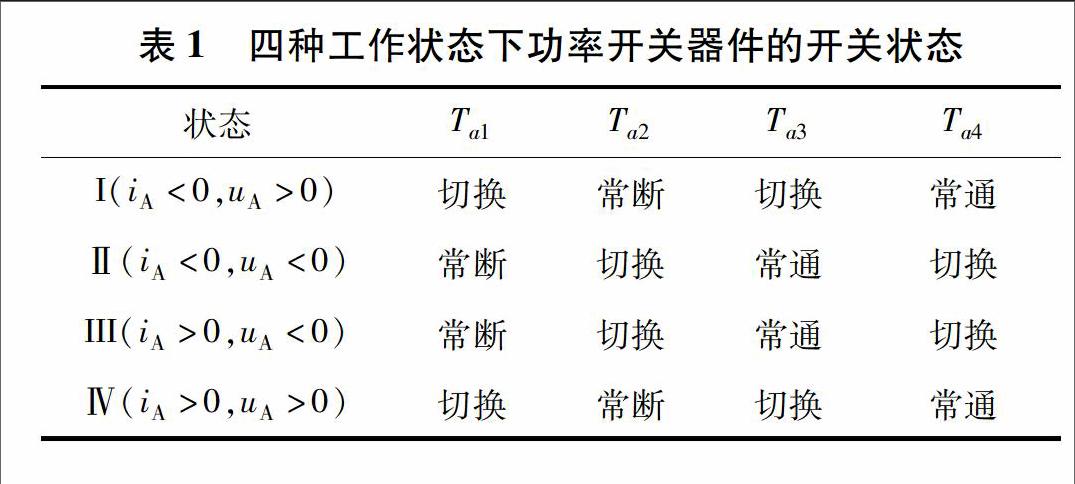
以A相为例分析TNPC型三电平SVG主电路的工作状态。设电流iA的正方向为从主电路流向电网。当iA<0，uA>0，时，主电路工作在第一种情况即为I，Ta2常断，Ta4常通，Ta1和Ta3作为PWM切换。当Ta1和Ta3分别加载驱动信号1和0时，电流流入电容C1正极，途中流经Tal的反并联二极管，A相输出的电平为高电平；当Ta1和Ta3加载驱动信号分别为0和1时，电流流经Ta4和Ta3的反并联二极管，A相输出的电平为零电平。同理，可得到另三种工作状态下器件的开关状态，如表1所示。

2无死区效应的控制策略

2.1死区效应分析

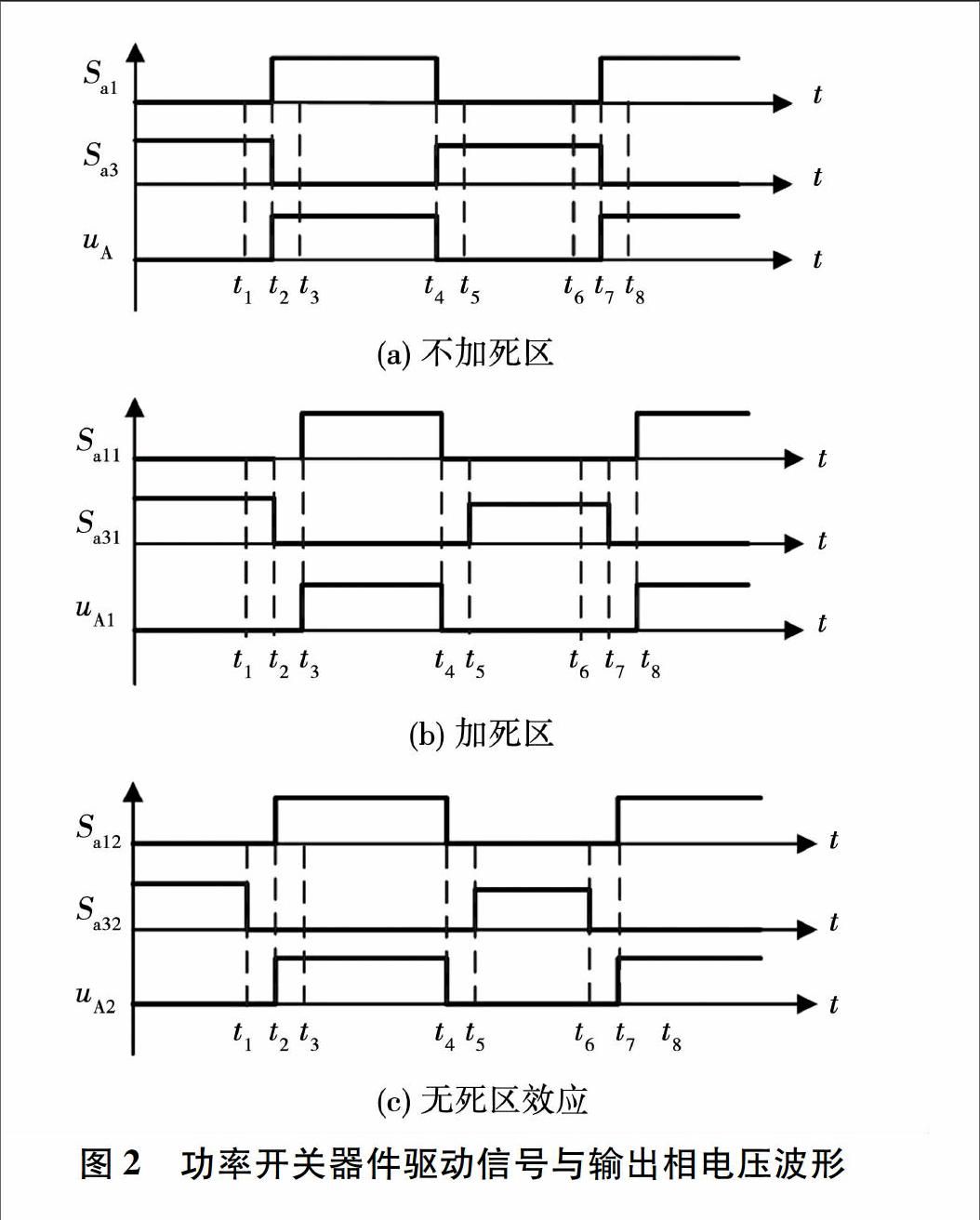
当TNPC型主电路中的A相工作在状态Ⅳ时，功率开关器件Ta2 、Ta4分别加0和1。分析时，都是将功率开关器件视为理想情况下，即导通和关断能够瞬间完成。不加死区时功率开关器件Ta1 、Ta3的驱动信号Sa1和 Sa3与输出相电压的关系如图2（a）所示。其中Ta3的信号与Ta1的信号互补，uA为A相输出的电压，t2～t4内电压为正的Udc/2，0～t2、t4～t7内电压为0。

在实际应用时则需要在信号中加入死区时间。加死区时Ta1 、Ta3的驱动信号Sa11、Sa31与输出相电压的关系如图2（b）所示。死区的加入，导致在t2～t3、t4～t5、t7～t8期间内驱动信号Sa11和Sa31的电平都为低电平，功率开关器件将Ta1和Ta3延时导通，此时电流流经Ta4和Ta3的反并联二极管最后流向连接电抗器。由图可知，uA1在t3～t4内电压为正的Udc/2，在0～t3和t4～t8内电压为0。Sa11、Sa31之间存在死区后，由于在死区时间内反并联二极管可以起到续流的作用，导致电压畸变，在其他三个工作状态中也会出现同样的现象。为了避免加入死区而带来的死区效应，通过调整驱动信号，来实现既存在死区又不会产生死区效应的功能。

在前面分析的基础上，对驱动信号进行了调整，如图2（c）中所示信号，Sa12、Sa32分别是调整后Ta1、Ta3的驱动信号，uA2为改进后A相输出的电压。Ta1仍然在t2～t4内导通，在0～t2 和t4～t7内关断，与图2（a）中的Sa1一样。而Ta3在0～t1和t5～t6内导通，即Ta3需要提前关断和滞后导通。在t1～ t2、t4～ t5、t6～ t7期间的驱动信号 Sa12和Sa32都为低电平，此时电流由Ta3 和Ta4的反并联二极管流向连接电抗器，输出电压uA2为0。t2～t4内uA2的电压为正Udc/2，0～t2、t4～t7内uA2电压为0。与图2（a）中的电压uA相比，可知uA2的导通关断时间与uA的导通关断时间相同。所以利用该方法不仅在互补的驱动信号之间加入了死区时间，而且通过反并联二极管的续流作用，在源头上避免了死区效应的生成[13]。

2.2无死区效应三载波层叠PWM法

通过以上分析，为了防止死区效应带来的危害，功率开关器件需要产生提前关断和滞后导通的驱动信号。本文在载波层叠PWM法的基础上进行改进，提出了无死区效应的三载波层叠PWM法[14]，如图3所示。其上层载波分别为相位超前载波ufu、原有载波uu、相位滞后载波uhu，下层载波分别为相位超前载波ufd、原有载波ud、相位滞后载波uhd。超前和滞后相位与需要的死区时间有关，在这里设载波移相时间为Ty，死区时间为Ts，则实际应用中使Ty=1.5Ts时，就可以保证互补驱动信号相差的相位满足死区要求。endprint

为了更清晰的分析三载波层叠调制法的工作原理把图3进行局部放大，如图4所示。

从图中可知，调制波与载波uu比较生成驱动信号Sua；与载波ufu比较生成提前导通的驱动信号Sfua和提前关断的驱动信号！Sfua；与载波uhu比较生成滞后关断的驱动信号Shua和滞后导通的驱动信号！Shua。同理，与下层原有载波ud比较生成驱动信号Sda，与载波ufd比较生成提前导通的驱动信号Sfda和提前关断的驱动信号！Sfda，与载波uhd比较生成滞后关断的驱动信号Shda和滞后导通的驱动信号！Shda。若此时iA>0，uA>0，TNPC型主电路工作在状态Ⅳ，Ta1的驱动信号S1为Sua，而Ta3的驱动信号S3为！Sfua&！Shua。

通过类似的分析，可以推导出不同工作状态下实现无死区效应的各功率开关器件的驱动信号，进而控制TNPC型SVG主电路中的功率开关器件，达到无功补偿的目的。表2给出了A相工作在不同状态时驱动信号的逻辑关系。

3仿真和实验分析

3.1仿真模型的建立

为了验证所设计系统和所提出方法的有效性，搭建了图5 所示的TNPC型三电平SVG系统的仿真模型。

在仿真中，选取电阻为15Ω、电感为50mH的三相对称的阻感负载。主电路和电网间的连接电阻为3Ω和串联电感为3mH，直流侧电容选5000μF。无功电流检测模块将三相电网电流信号进行dq变换，分离出有功分量与无功分量，让SVG补偿电流的无功分量跟踪电网的无功分量，实现电流闭环。调节直流侧电容电压跟踪给定电压值，实现电压闭环。PWM信号生成模块根据检测到的SVG补偿电流的方向和连接电抗器的电压极性，判断主电路的工作状态，通过无死区效应载波层叠PWM算法产生多路PWM信号，根据主电路的工作状态将多路PWM信号进行逻辑组合，生成无死区效应的驱动信号，驱动SVG补偿电网无功功率。

3.2仿真结果及分析

在所建立的仿真模型的基础上进行了有死区和无死区效应两种驱动方式下的仿真实验，得到SVG加入前后电网电压和电流的波形，如图6所示。

图6（a）是传统直接在PWM信号后加入死区后的补偿效果图，由图可知SVG补偿前电流滞后电压，在0.06s时SVG投入运行，电路迅速补偿但电流并没有完全与电压同相位，而是存在一定的相位差。图6（b）是无死区效应产生驱动信号的方法，在其他仿真参数相同的情况下，在0.06s时SVG投入运行，电流迅速调整到与电压同相位。可见无死区效应的TNPC型三电平SVG能够快速地对无功功率进行补偿。

图7（a）为直接加入死区时SVG补偿后电网的功率因数，由图可知采用这种驱动信号时补偿后的功率因数为0.96左右，说明加入死区后，对SVG补偿电网的无功功率造成一定的影响，图7（b）为采用无死区效应的SVG补偿后的功率因数曲线，补偿后功率因数稳定在0.99。证明本文设计的无死区效应的控制策略能有效的提高功率因数，具有实际的应用意义。

3.3实验验证

在前面理论研究和仿真验证的基础上，设计了无死区效应的TNPC型三电平SVG硬件和相应的软件。硬件设计主要包括检测调理电路、辅助电源和驱动电路等。软件部分主要阐述了主程序、中断程序、无死区效应的载波层叠PWM程序等。选用TMS320F2812作为主处理器，EP2C35F484C8N作为从处理器，搭建了TNPC型三电平SVG的实验平台，如图8所示，针对阻感负载进行了实验。

补偿前电网中电压与电流的波形图如图9所示，从图中可知电流滞后电压46°左右。图10所示为补偿后电网中电压与电流的波形图，可见电流滞后电压1°左右，证明本文所设计的SVG能够对阻感性负载产生的无功功率进行有效的补偿。

4结论

本文将TNPC型三电平逆变电路引入到静止无功发生器，构架了TNPC型三电平静止无功发生器的总体方案。在分析TNPC型三电平主电路工作状态和死区效应的基础上，提出了无死区效应的三载波层叠PWM控制方法，并在MATLAB中进行了仿真验证。仿真结果表明，采用无死区效应控制策略的SVG对电网的无功功率补偿效果好，补偿后电网的功率因数得到了提高，证明了本文设计的SVG的可行性与正确性。最后在理论研究和仿真验证的基础上，搭建了实验平台，并对阻感负载下SVG补偿无功功率的情况进行了实验。实验结果证明对本文所设计的无死区效应的控制策略可以使SVG系统对电网进行更好的无功补偿。

参 考 文 献：

[1]AGHDAM， G.H. Optimised Active Harmonic Elimination Technique for Threelevel Ttype Inverters [J]. IET Power Electron（S1755-4535）， 2013， 6（3）： 425-433.

[2]MARIO Schweizer. Design and Implementation of a Highly Efficient ThreeLevel TType Converter for LowVoltage Applications [J]. IEEE TRANSACTIONS ON POWER ELECTRONICS（S0885-8993）， 2013， 28（2）： 899-907.

[3]劉军锋， 李叶松. 死区对电压型逆变器输出误差的影响及其补偿 [J]. 电工技术学报， 2007， 22（5）： 117-121.

[4]张百乐， 王久和， 赵风姣. TNPC型光伏并网逆变器的PCHD建模与控制 [J]. 中国电机工程学报， 2014， 34（S1）： 204-210.

[5]徐先勇，欧朝龙，罗安，等. 新型近似无死区PWM逆变器开关控制方法及其特性分析[J]. 电力自动化设备，2011，08（31）：66-71.

[6]王勇，高宁，罗悦华，等. 三相三电平并网逆变器无死区SPWM控制研究[J]. 中国电机工程学报，2011，21（31）：70-75.

[7]CASTRO LM，ACHA E，FUERTEESQUIVEL C R. A Novel STATCOM Model for Dynamic Power System Simulations[J]. IEEE Transactions on Power Systems，2013，28（3）：3145-3154.

[8]刘栋良， 武瑞斌， 张遥， 等. 基于模糊控制零电流钳位逆变器死区补偿 [J]. 电工技术学报， 2011， 26（8）： 119-124.

[9]CHEN Lihua，PENG Fangzheng.Deadtime Elimination for Voltage Source Inverters[J]. IEEE Transactions on Power Electronics，2008，23（2）：574-580.

[10]杨立永， 陈智刚， 陈为奇， 等. 逆变器输出电压模型及新型死区补偿方法 [J]. 电工技术学报， 2012， 27（1）： 182-186.

[11]杨荣峰，随顺科，徐榕，等. 级联SVG控制策略及死区技术补偿研究[J]. 电机与控制学报，2014，10（18）：37-41.

[12]宋崇辉，刁乃哲，薛志伟，等. 新型多重载波无死区SPWM[J]. 中国电机工程学报，2014，12（34）：1853-1863.

[13]周京华，贾斌，章小卫，等. 三电平逆变器死区补偿策略研究[J]. 电机与控制学报，2013，05（17）：69-74.

[14]李文娟，冯杰. TNPC型逆变器无死区载波层叠PWM控制[J].系统仿真学报，2016，38（7）：1628-1636.

（编辑：王萍）endprint