带1-范数约束的分裂可行问题的投影算法
2017-11-06畅含笑
畅含笑,屈 彪
(曲阜师范大学管理学院,山东日照 276826)
带1-范数约束的分裂可行问题的投影算法
畅含笑,屈 彪
(曲阜师范大学管理学院,山东日照 276826)
本文主要研究带1-范数约束的分裂可行问题的求解算法.用一种交替投影算法,求得了问题的解,提出松弛交替投影算法,改进了直接往闭凸集上投影这一不足,并证明了该算法的收敛性.
分裂可行问题;1-范数约束;交替投影;松弛
1 引言
由于社会的发展和生产实践的需求,最优化问题在金融、医学、药学以及手工农业等领域受到越来越多的重视,分裂可行问题就是其中之一.1994年,Censor和Elfving依据医学中有关放射治疗的实践经验和理论提出了分裂可行问题[1],问题形式如下

其中C,Q分别为RN和RM中的非空闭凸集,A为一个M×N的实矩阵.
随后,分裂可行问题的拓展形式被学者们相继提出.本文主要研究的是带1-范数约束的分裂可行问题的解,问题形式如下

其中‖.‖1代表1-范数,s>0为一个给定的常数.
目前,大多数关于求解分裂可行问题及其拓展问题的算法,要么牵涉到往闭凸集上的投影,而这一投影在实际操作中难以实现;要么在求解合适的步长过程中需要估算相关矩阵的最大特征值、Lipschitz系数或进行线搜索,而这些操作往往需要大量的计算.关于求解分裂可行问题的1-范数解问题已有学者在研究[14,15].在文献[14]中,作者将分裂可行问题的1-范数解问题转化为变分不等式问题进行求解,但在其给出的算法中需要估算矩阵的最大特征值.
在文献[2]中,对于多集分裂可行问题
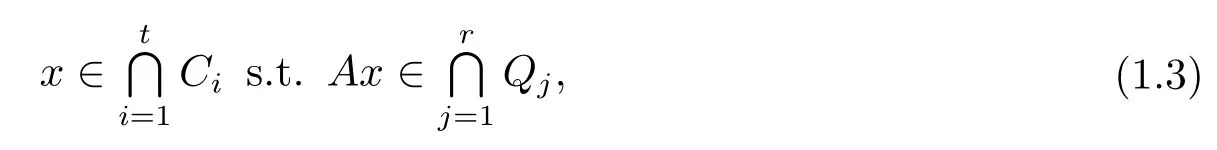
其中Ci(i=1,2,···,t)和Qj(j=1,2,···,r)分别为RN和RM中的非空闭凸集.
作者提出了一种序列投影算法

显然,序列投影算法有可以直接计算的步长,从而避免了在求解步长时进行大量的计算.受到文献[2]的启发,将问题(1.2)转化为如下形式

其中D={x|‖x‖1≤s}.
序列投影算法虽有可以直接计算的步长,但却牵涉到往闭凸集上的投影.首先,本文在序列投影的基础上,提出交替投影算法求解了问题(1.4).其次,考虑到在实际操作中往闭凸集上的投影是难以实现的,文章后半部分构造包含C,D,Q的半空间,利用到半空间上的投影来代替到闭凸集上的投影,从而使投影得到了顺利实现.
2 预备知识
定义1[3,4]设Ω⊂RN为非空闭凸集,对任意的x∈RN,定义
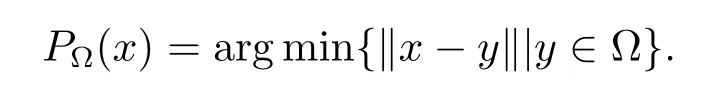
并称其为x到Ω上的投影.显然,若x∈Ω,则x=PΩ(x).
注1由投影的定义,可以得出问题(1.2)等价于如下带约束的最小化问题
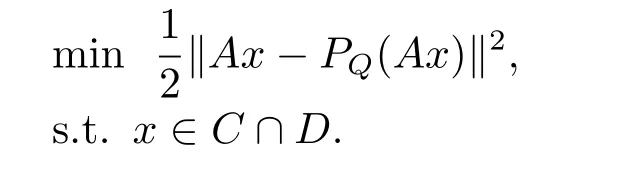
定义2[3]给定正常凸函数f:RN→(−∞,+∞],对任意一点x∈domf,若向量ξ∈RN满足
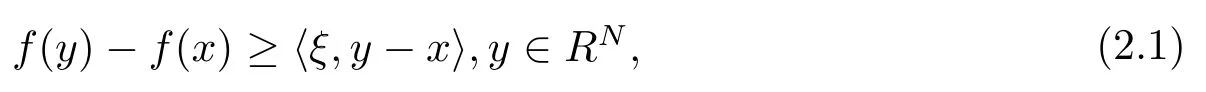
则称ξ为凸函数f在点x处的次梯度.将满足式(2.1)的向量ξ的全体构成的集合记为∂f(x),并称之为f在x处的次微分.
注2domf表示f的有效域,即domf={x∈RN|f(x)<+∞}.若f在x处可微,则满足(2.1)式的ξ存在且唯一,并且易知该向量即梯度▽f(x).
由次梯度的定义,简单计算可得f(x)=‖x‖1在x∈RN的次梯度t,其分量为

引理2.1[9]设Ω为RN中的非空闭凸集,则对于投影算子PΩ(.),下述结论成立.
(a)〈PΩ(x)−x,z−PΩ(x)〉≥0,∀x∈RN,z∈Ω;
(b)‖PΩ(x)−PΩ(y)‖ ≤ ‖x−y‖,∀x,y∈RN;
(c)‖PΩ(x)−z‖2≤ ‖x−z‖2−‖PΩ(x)−x‖2,∀x∈RN,z∈Ω;
(d)‖PΩ(x)−PΩ(y)‖2≤ ‖x−y‖2−‖PΩ(x)−x+y−PΩ(y)‖2,∀x,y∈RN.
引理2.2[3]假设f:RN→R为凸函数,则f在RN上处处次可微且次微分在RN的任意有界子集上一致有界.
引理2.3[4]设a∈RN,b∈R,则u∈RN到半空间{x∈RN|aTx≥b}上的投影为

引理2.4[16]设f:RN→(−∞,+∞]为闭正常凸函数.给定满足xk→x的点列{xk}⊆RN,若ξk∈ ∂f(xk)且ξk→ ξ,则有ξ∈ ∂f(x).
3 算法及收敛性分析
此部分给出问题(1.4)的求解算法.
3.1 交替投影算法
本文采用可以直接计算的步长,避免了在求合适步长时,进行大量的计算.在该算法中,假设到闭凸集上的投影是可以直接计算的,且问题(1.4)的解集非空.
算法3.1
步骤1任取x0∈RN,选取
步骤2令
步骤3计算
引理3.1设x∗为问题(1.4)的任意解,{xk}为算法3.1产生的点列,则数列{‖xk−x∗‖}收敛.
定理3.1设{xk}为算法3.1产生的点列,则{xk}收敛到问题(1.4)的一个解.
注3算法3.1可以看成[2]中序列投影算法的特例,引理3.1、定理3.1的证明过程可分别参看文献[2]中引理2.2、定理2.1.
3.2 松弛交替投影算法
由于算法3.1牵涉到往闭凸集上的投影,所以针对这一不足对算法3.1进行改进.这里,寻找包含集合C,D,Q的半空间,利用到半空间上的投影来代替到闭凸集上的投影,从而使投影简单可行.
在该部分,将集合D={x∈RN|‖x‖1≤s}记为D={x∈RN|f(x)≤0},其中f(x)=‖x‖1−s.
假设C,Q满足如下条件:
(H1)C={x∈RN|c(x)≤0},其中c:RN→R是凸函数(不需要可微的)且C是非空的.Q={y∈RM|q(y)≤0},其中q:RM→R是凸函数(不需要可微的)且Q是非空的.
(H2)对于任意的x∈RN,至少有一个次梯度ς∈∂c(x)是可以计算的,其中∂c(x)={ς∈RN|c(z)≥c(x)+〈ς,z−x〉,∀z∈RN}.
对于任意的y∈RM,至少有一个次梯度η∈∂q(y)是可以计算的,其中∂q(y)={η∈RM|q(u)≥q(y)+〈η,u−y〉,∀u∈RM}.并且构造包含C,D,Q的半空间Ck,Dk,Qk如下
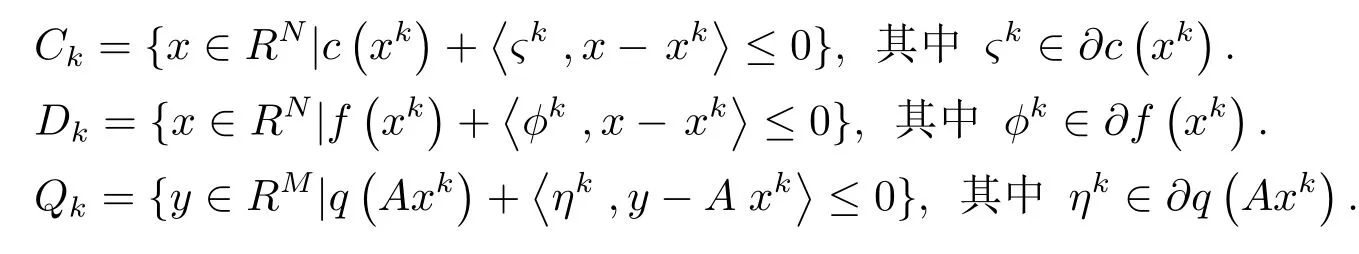
注4由次梯度的定义,容易得出∀k∈N,有C⊂Ck,D⊂Dk,Q⊂Qk.
算法3.2
步骤1任取x0∈RN,选取
步骤2令
步骤3计算
其中Ck,Dk,Qk如上文所述.
注5在实际计算中,
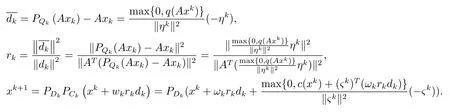
令
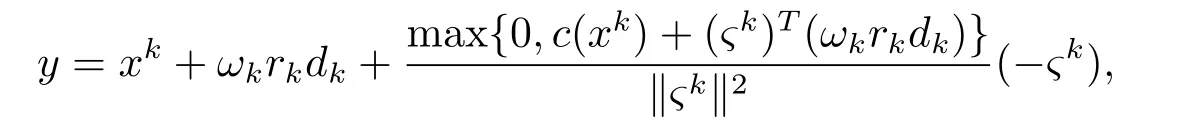
则
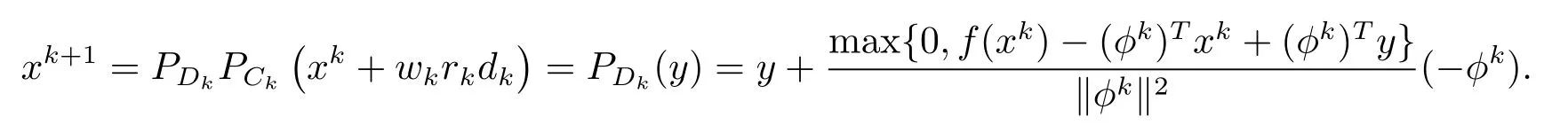

注6由(3.1)式及Ck的定义,显然Ck=C(xk).在式(3.1)中,可以取满足如下条件的由引理2.4知
引理3.2若点列收敛到收敛到则其中中满足
证由引理2.3得


证毕.
引理3.3设x∗为问题(1.4)的任意解,为算法3.2产生的点列,则数列收敛.
证因为x∗为问题(1.4)的任意解,所以x∗∈C∩D,Ax∗∈Q,由引理2.1(a)得
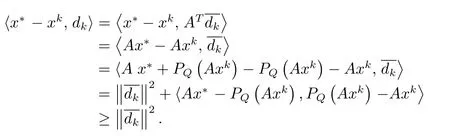
又因为x∗∈C⊂Ck,x∗∈D⊂Dk,所以
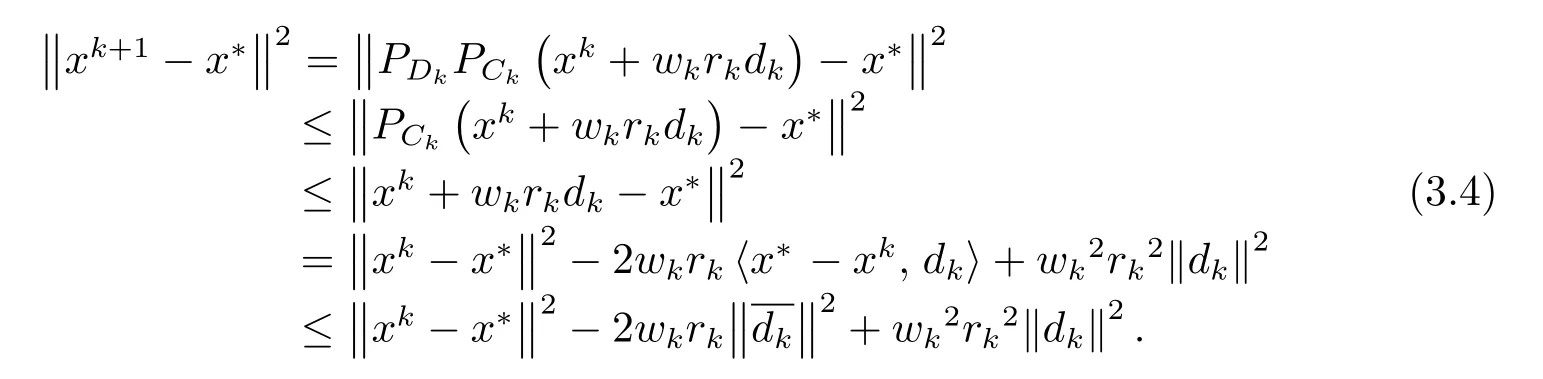

注7由(3.4)式的最后一步可以得出,当时,取得最小值,也即xk最接近x∗.
定理3.2设为算法3.2产生的点列,若问题(1.4)的解集非空,则收敛到问题(1.4)的一个解.
证设x∗为问题(1.4)的任意解,由引理3.2知数列收敛,同时序列有界.更进一步,由(3.5)式得又因为有界,所以即
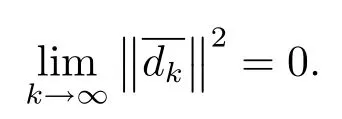
也就是


由引理2.1(b),(c)可得
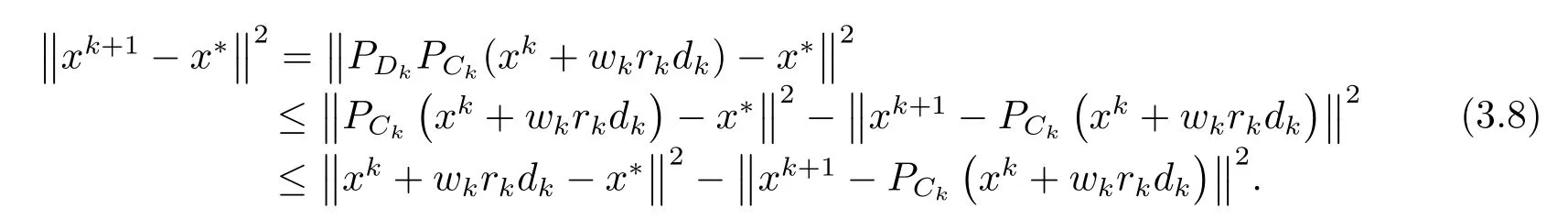
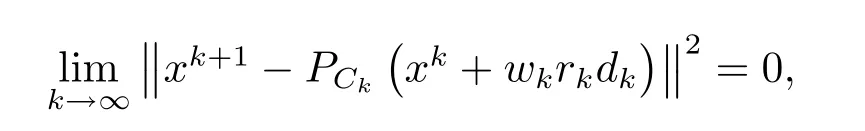
从而

由(3.9)式得
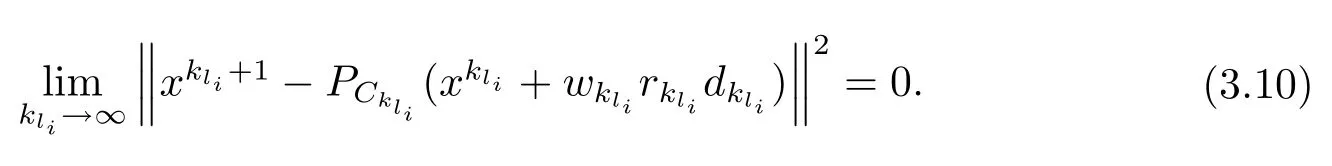
由引理3.2,对(3.10)式取极限得





证毕.
4 数值实验
为了验证本文所给算法3.2的可行性,给出如下几个例子.下面的例1–6取s=1.2,s=3两种情况来验证.首先给出的例1–4,集合C与Q都是由可微凸函数的水平集来定义的;其次给出的例5–6,集合C与Q为不可微凸函数的水平集来定义的.最后给出的例7选取高维的水平集和随机的矩阵.在实际计算中选取参数ωk=1.


例1–6的数值结果如下表1.1–6.2.在表1.1–7.1中,x0代表初始点,Iter代表迭代步数,cpu代表计算时间(单位为秒),x∗代表近似解(以下这些结果都是运用MATLAB计算得到的).

表1.1:例1(s=1.2)的数值结果

表1.2:例1(s=3)的数值结果

表2.1:例2(s=1.2)的数值结果

表2.2:例2(s=3)的数值结果
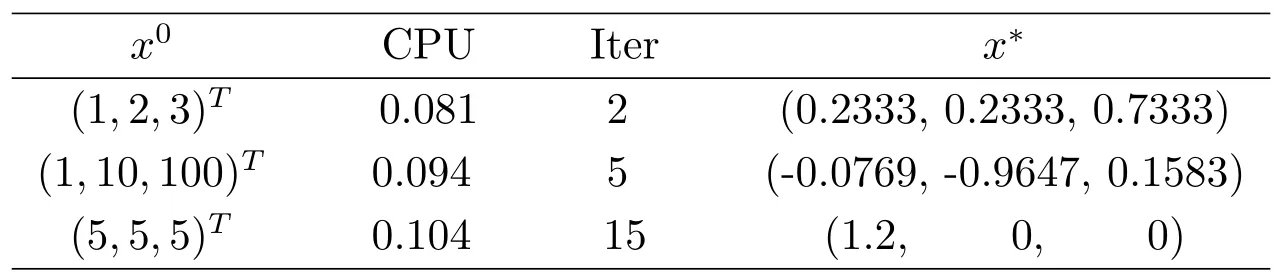
表3.1:例3(s=1.2)的数值结果
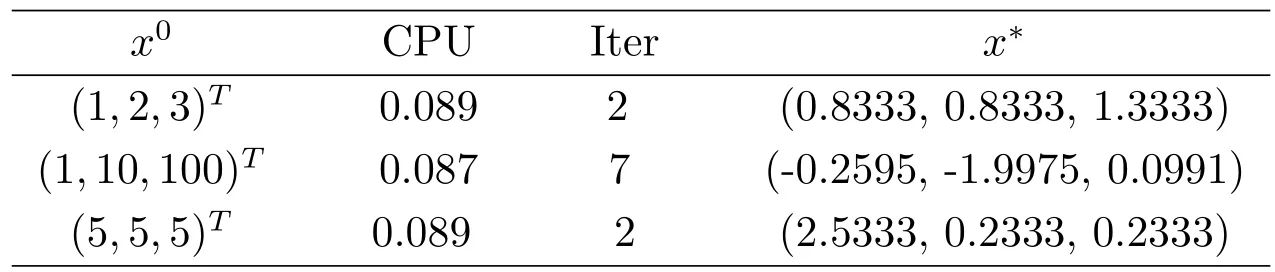
表3.2:例3(s=3)的数值结果

表4.1:例4(s=1.2)的数值结果

表4.2:例4(s=3)的数值结果

表5.1:例5(s=1.2)的数值结果
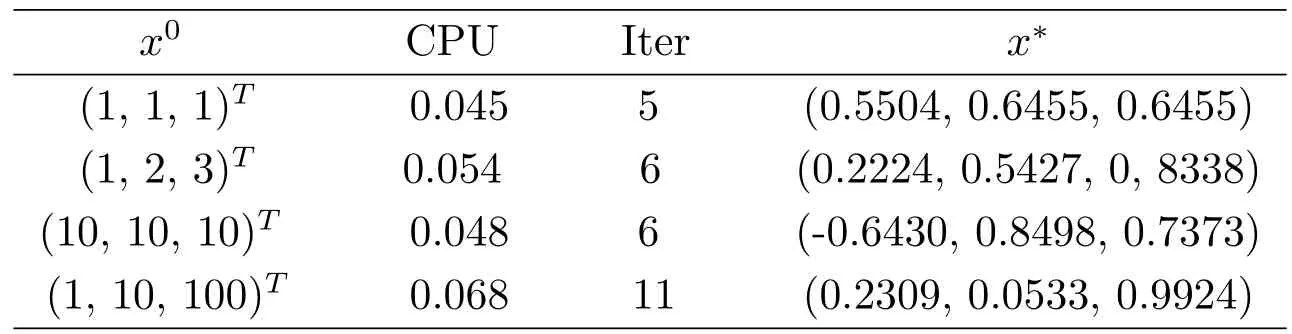
表5.2:例5(s=3)的数值结果

表6.1:例6(s=1.2)的数值结果

表6.2:例6(s=3)的数值结果
例7的数值结果如下表,由于选取的水平集为高维的、矩阵是随机的,所以给出的计算结果中不显示近似解.

表7.1:例7(s=0.12)的数值结果
从例1–7的数值实验结果可以看出,所有的计算时间都在0.1秒左右完成,甚至大多数的计算时间都在0.1秒以内.由此可见松弛交替投影算法具有较强的可行性和实用性.
5 本文小结
本文主要对带1-范数约束的分裂可行问题进行了求解.首先,在算法上取了可以直接计算的步长,避免了在求合适的步长时进行大量的计算.其次,又寻找包含闭凸集的半空间,用往半空间上的投影来代替往闭凸集上的投影,从而提出松弛交替投影算法,使得投影容易计算.并给出几个实例来验证松弛交替投影算法的可行性.数值实验表明本文的算法具有较强的可行性和实用性.
[1]Censor Y,Elfving T.A multiprojection algorithm using Bregman projection in a product space[J].Numer.Alg.,1994,8(2):221–239.
[2]Liu B,Qu B.A successive projection scheme for solving the multiple-sets split feasibility problem[J].Numer.Funct.Anal.Optim.,2014,35(11):1459–1466.
[3]Rockafellar R T.Convex analysis[M].Vol.28,Princeton:Princeton Math.Ser.,1970.
[4]王宜举,修乃华.非线性最优化理论与方法[M].北京:北京科学出版社,2012.
[5]Qu B,Xiu N.A note on the CQ algorithm for the split feasibility problem[J].Inverse Prob.,2005,21:1655–1665.
[6]Censor Y,Elfving T,Kopf N,et al.The multiple-sets split feasibility problem and its applications for inverse problems[J].Inverse Prob.,2005,21:2071–2084.
[7]Yang Q.The relaxed CQ algorithm solving the split feasibility problem[J].Inverse Prob.,2004,20(4):1261–1266.
[8]Zhang H,Wang Y.A new CQ method for solving split feasibility problem[J].Front.Math.China,2005,5(1):37–46
[9]Facchinei F,Pang J S.Finite-dimensional variational inequalities and complementarity problems[M].Vols.I and II,Berlin:Springer Verlag,2003.
[10]Qu Biao,Liu Bing-hua and Zhengna.On the computation of the step-size for the CQ-like algorithms for the split feasibility problem[J].Appl.Math.Comp.,2015,262:218–223.
[11]Carmi A,Censor Y and Gurfil P,Convex feasibility modeling and projection methods for sparse signal recovery[J].J.Comp.Appl.Math.,2012,236(17):4318–4335.
[12]Amir Beck,Yonina C Eldar.Sparsity constrained nonlinear optimization conditions and algorithms[J].SIAM Optim.,2012,23(3):1480–1509.
[13]Fukushima M.An outer approximation algorithm for solving general convex programs[J].Opera.Res.,1983,31:101–113.
[14]He H,Ling C,Xu H.An implementable splitting algorithm for the 1-norm regularized split feasibility problem[J].J.Sci.Comput.,2016,67:281–289.
[15]He S,Zhu W.A note on approximating curve with 1-norm regularization method for the split feasibilit problem[J].J.Appl.Math.,2012,16:3800–3844.
[16]Massao Fukushima.非线性最优化基础[M].北京:科学出版社,2011.
[17]兰晓坚,曲彪.求解分裂可行问题的一种半空间投影算法[J].数学杂志,2011,31(3):547–553.
[18]房明磊,朱志斌,陈凤华,张聪.互补约束规划问题的一个广义梯度投影算法[J].数学杂志,2011,31(4):685–694.
PROJECTION ALGORITHMS FOR THE SOLUTION OF SPLIT FEASIBILITY PROBLEM WITH 1-NORM CONSTRAINTS
CHANG Han-xiao,QU Biao
(School of Management,Qufu Normal University,Rizhao 276826,China)
In this paper,we mainly study the solution algorithm of the split feasibility problem subject to 1-norm constraints.By using the alternating projections algorithm,we solve the problem successfully and propose arelaxed alternating projections algorithm which improves the shortage of projecting directly onto the closed convex set.And we obtain the convergence of this algorithm.
split feasible problem;1-norm constraints;alternating projections;relaxed
90C25;65K05
O221.2
A
0255-7797(2017)06-1234-11
2016-03-11接收日期:2016-06-28
国家自然科学基金(11271226);山东省优秀中青年科学家科研奖励基金(BS2012SF027).
畅含笑(1990–),女,河南开封,硕士,主要研究方向:非线性规划.
