距离模式识别图的判定

丁超

(安庆师范大学数学与计算科学学院,安徽安庆 246133)

距离模式识别图的判定

丁超

(安庆师范大学数学与计算科学学院,安徽安庆 246133)

本文研究了几类图的距离模式识别性.利用构造法,求出了它们的距离模式识别集和距离模式识别数,提出距离模式识别率的概念,推广了距离模式识别数的概念.

距离模式识别集;距离模式识别数;方格图

1 引言

图的距离模式识别集由Acharya在2006年向Germina提出,随后Germina等人对此展开了研究,一些有意思的结论见文献[1–8].图的一个距离模式识别集是图的一个自同构群,图的每个顶点可由它与距离模式识别集的关系所唯一确定.图可能存在距离模式识别集也可能不存在距离模式识别集,存在距离模式识别集的图称为距离模式识别图,否则称为非距离模式识别图.图G的距离模式识别集可能不唯一,阶数最小的距离模式识别集的阶数称为图的距离模式识别数(记为ρ(G)).如何判定图的距离模式识别数是个有意思的问题.本文判定两类非距离模式识图,得到几类图的距离模式识别集和距离模式识别数,最后给出一个计算距离模式识别率的算法.

2 定义和引理

定义2.1[1]设v为图G(V,E)的任意一个顶点,非空集合M⊆V(G),j为非负整数,记,称集合fM(v)={d(u,v):u∈M}为v的M-距离模式.显然,.如果是单射,那么称M为G的距离模式识别集.记n×(dG+1)阶矩阵为G的直径),将中的非零元用1替换得矩阵

定义2.2设G1(V1,E1)和G2(V2,E2)为两个简单图,它们的积图G1×G2定义为

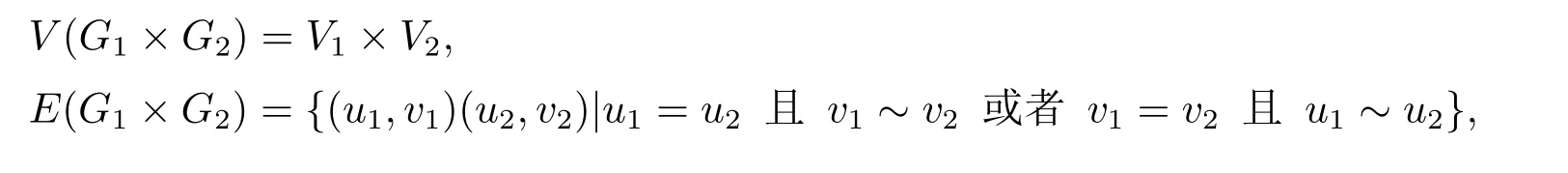
其中v1～v2表示v1与v2在G2中邻接,u1～u2表示u1与u2在G1中邻接,若G1和G2为两条路,则它们的积图为方格图.

引理2.3[2]设图为G(V,E),非空集合M⊆V(G),M为G的距离模式识别集的充分必要条件是的任意两行互异.

例2.4图1给出了两个图,其中G为距离模式识别图,H为非距离模式识别图.

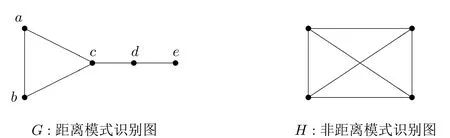
图1

在G中,令M={b,c,e},则

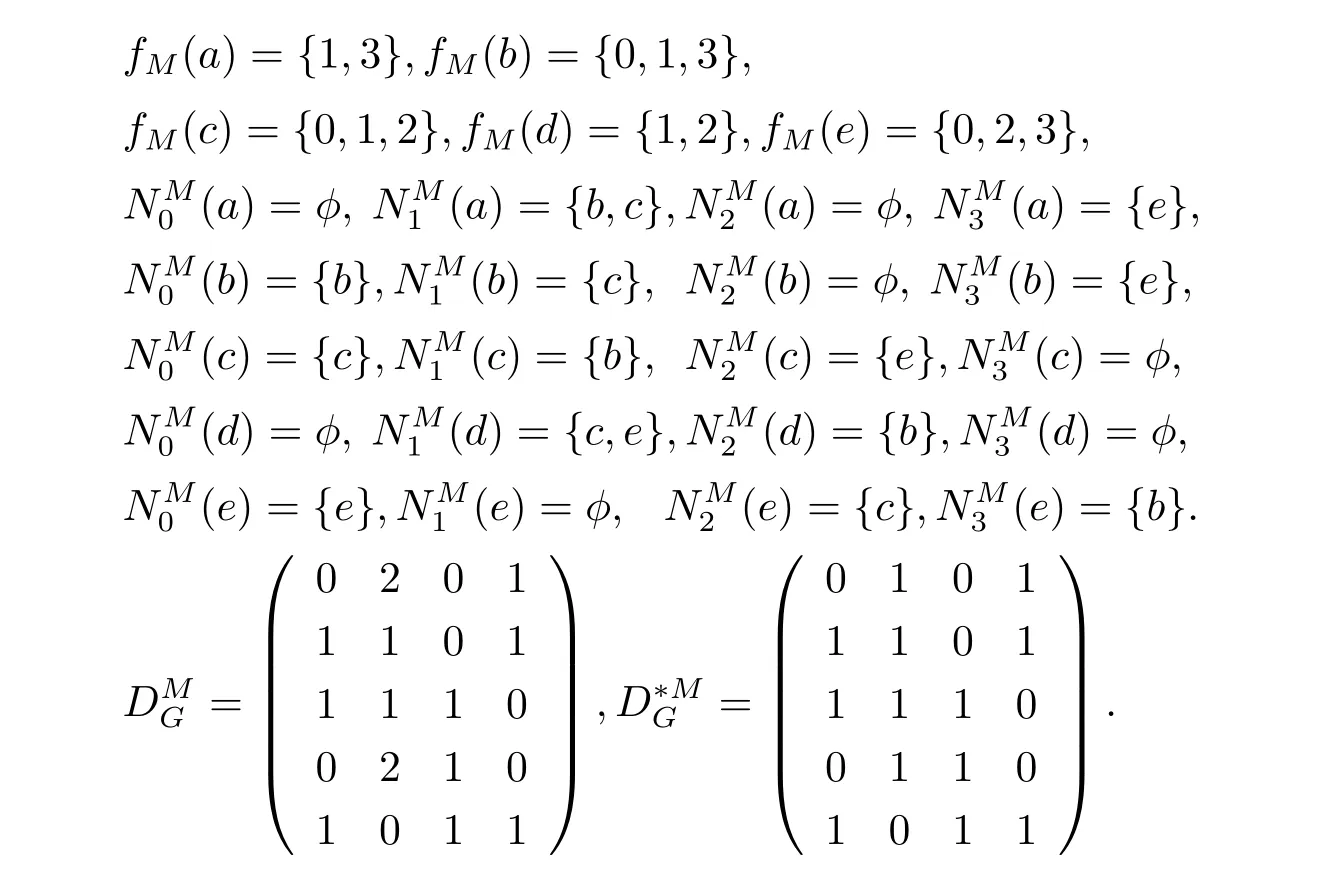
的任意两行互异,所以M为G的距离模式识别集,即G为距离模式识别图,且ρ(G)=3.H不存在距离模式识别集,即H为非距离模式识别图.

引理2.5[2]设Cn为n阶圈,则Cn为距离模式识别图的充分必要条件是n≥7.

引理2.6[3]设G为距离模式识别图,M为G的距离模式识别集.那么M的导出子图G[M]是非连通的.

引理2.7[1](a)平凡图K1是唯一的距离模式识别数为自身价数的图.

(b)路是唯一的距离模式识别数为1的图.

(c)不存在距离模式识别数为2的图.

(d)若n≥7,则ρ(Cn)=3.

3 主要结论

定理3.1(a)设G为任意给定的图,v为G的任一顶点,H1为G在点v粘三个悬挂点所得的图,则H1为非距离模式识别图.

(b)设树T∗如图2所示,将T∗粘到(在点v处)任一图的任一顶点上得H2,则H2为非距离模式识别图.

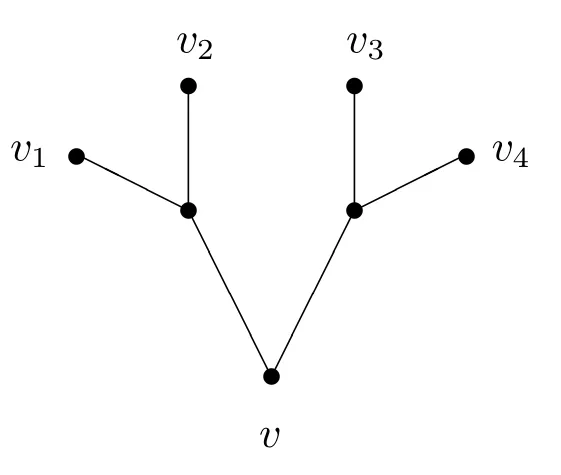
图2

证(a)设粘到点v上的三个悬挂点分别为v1,v2,v3.假设H1有一个距离模式识别集M,对v1,v2,v3而言有以下两种情形:

情形1v1,v2,v3中至少有两个顶点属于M.不失一般性,令v1,v2属于M,那么在中对应于v1,v2的两行相同,与M为距离模式识别集矛盾.

情形2v1,v2,v3中至少有两个顶点不属于M.不失一般性,令v1,v2属于M,那么在

中对应于v1,v2的两行也相同,与M为距离模式识别集矛盾.

(b)设树T∗的四个悬挂点分别为v1,v2,v3,v4.假设H2有一个距离模式识别集M,对v1,v2,v3,v4而言也有至少两个顶点属于M或者至少两个顶点不属于M的两种情形,证明与(a)相同.所以结论成立.

定理3.2设Cn为n(n≥3)阶圈,Pm为m(m≥2)阶路,将Pm的一个悬挂点粘到Cn的一个顶点上得图H.当m=2且n=3或者n=4时,H为非距离模式识别图.其它情形H为距离模式识别图,且ρ(H)=3.

证 情形1n=3且m=2.设C3=v1v2v3v1,P1=v1v4是粘到v1上的路.假设H有一个距离模式识别集M.由引理2.7知|M|≠1,2,4,那么M只能是{v2,v3,v4},但在中对应于v2,v3的两行相同,与M为距离模式识别集矛盾,即H为非距离模式识别图.

情形2n=3且m＞2.设C3=v1v2v3v1,Pm=v1v4v5···v2+m是粘到v1上的路.考察集合M={v1,v3,v5},则

情形3n=4且m=2.设C4=v1v2v3v4v1,P1=v1v5是粘到v1上的路.假设H有一个距离模式识别集M.由引理2.6和引理2.7知|M|≠1,2,4,5,那么M只能是{v1,v3,v5},{v3,v4,v5},{v2,v3,v5}和{v2,v4,v5}.容易验证对应的中总有两行相同,与M为距离模式识别集矛盾,即H为非距离模式识别图.

情形4n=4且m＞2.设C4=v1v2v3v4v1,Pm=v1v5v6···v3+m是粘到v1上的路.考察集合M={v1,v2,v6},则

情形5n=5且m≥2.设C5=v1v2v3v4v5v1,Pm=v1v6v7···v4+m是粘到v1上的路.考察集合M={v1,v3,v6},则

情形6n=6且m≥2.设

是粘到v1上的路.考察集合M={v1,v3,v7},则

情形7n≥7且m≥2.设

由定理3.2的证明不难得出下面推论.

推论3.3设G为距离模式识别图,Pm为m(≥2)阶路,将Pm的一个悬挂点粘到G的一个顶点上得图H,且dH=dG+m−1,则H为距离模式识别集,且ρ(H)=ρ(G).

定理3.4设Pm,Pn分别是m阶和n阶路,G=Pm×Pn是一个格子图(m≥2,n≥4,n＞m),则G为距离模式识别图,且ρ(G)=3.

证 设

如果M是G的一个距离模式识别集,则|M|≥3.考察集合M={v11,v12,v1n},有两种情形.

情形1n为奇数.在中对应点v11,v12,···,v1n的行所形成的子矩阵记为D1,则D1为

D1中的任意两行互异,记Di为中对应点vi1,vi2,···,vin的行所形成的子矩阵,则Di+1中的元素1的位置由Di中的元素1的位置向右移一个单位得到(i=1,2,···,m−1).所以的任意两行互异,M为G的距离模式识别集,即G为距离模式识别图,且ρ(G)=3.

情形2n为偶数.在中对应点v11,v12,···,v1n的行所形成的子矩阵记为D1,则D1为

后面的证明与情形1相同.所以结论成立.

4 算法

设图G(V,E)为简单图,非空集合M⊆V(G),记rM为所有行构成的集合的阶,称为G的距离模式识别率,当µ(G)=1时G为距离模式识别图,当µ(G)＜1时G为非距离模式识别图.以下给出计算图的距离模式识别率和距离模式识别数的算法:

第一步利用弗洛伊德算法计算G的距离矩阵D.

第二步求出G的所有n×k阶子阵D′以及与D′对应的顶点集M(其中1≤k≤n且k≠2).

第三步求出M对应的以及rM.

第四步计算距离模式识别率,当µ(G)=1时,输出所有距离模式识别集M,转第五步.

第五步计算距离模式识别数ρ(G)=min|M|.

[1]Sona J,Germina K A.On the distance pattern distinguishing number of a graph[J/OL].J.Appl.Math.,Article ID 328703,8 pages,2014.

[2]Germina K A.Set-valuations of graphs and applications[R].Project Completion Report DST Grant-In-Aid Project No.SR/S4/277/05.Dpt.Sci.Tech.(DST),Government of India,2011.

[3]Germina K A,Joseph A.Some general results on distance pattern distinguishing graphs[J].Intern.J.Contem.Math.Sci.,2011,6(15):713–720.

[4]Chartrand G,Eroh L,Johnson M A,Oellermann O R.Resolvability in graphs and the metric dimension of a graph[J].Disc.Appl.Math.,2000,105(3):99–113.

[5]Khuller S,Raghavachari B,Rosenfeld A.Landmarks in graphs[J].Disc.Appl.Math.,1996,70(3):217–229.

[6]Germina K A,Joseph A,Sona J.Distance neighbourhood pattern matrices[J].Euro.J.Pure Appl.Math.,2010,3(4):748–764.

[7]Germina K A.Distance-Patterns of vertices in a graph[J].Intern.Math.Forum,2010,5(34):1697–1704.

[8]Chartrand G,Poisson C,Zhang P.Resolvability and the upper dimension of graphs[J].Comp.Math.Appl.,2000,39(12):19–28.

DETERMINATION OF DISTANCE PATTERN DISTINGUISHING GRAPHS

DING Chao
(School of Mathematics and Computational Science,Anqing Normal University,Anqing 246133,China)

In this paper,some classes of graphs are studied on distance pattern distinguishing.By the method of structuring,their distance pattern distinguishing sets and the distance pattern distinguishing numbers are given.The concept of distance pattern distinguishing rate is proposed,which extends the concept of distance pattern distinguishing number.

distance pattern distinguishing graph;distance pattern distinguishing number;grid

05C12

O157.5

A

0255-7797(2017)06-1220-07

2016-07-16接收日期:2016-10-31

安徽省高等学校自然科学基金资助(KJ2013186).

丁超(1979–),男,安徽芜湖,讲师,主要研究方向:图论.