COMPOSITION OF PSEUDO AUTOMORPHIC STOCHASTIC PROCESS AND APPLICATIONS

ZHOU Hui,ZHOU Zong-fu,QIAO Zong-min

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei 230061,China)

(2.School of Mathematical Science,Anhui University,Hefei 230039,China)

COMPOSITION OF PSEUDO AUTOMORPHIC STOCHASTIC PROCESS AND APPLICATIONS

ZHOU Hui1,ZHOU Zong-fu2,QIAO Zong-min1

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei 230061,China)

(2.School of Mathematical Science,Anhui University,Hefei 230039,China)

In this paper,a composition theorem for pseudo-almost automorphic stochastic process is established under a weaker Lipschitz condition.The composition theorem is more general than some known results.Using these properties,we obtain the existence and uniqueness of pseudoalmost automorphic mild solutions for a class of stochastic differential equations.

pseudo-almost automorphic;composition;square-mean;mild solution

Huang and Yang[14]established some criteria ensuring the existence and uniqueness of almost periodic solutions for the following stochastic equations with delays

In recent papers,Cao et al.[15]concerned with the existence of square-mean almost periodic mild solutions for stochastic differential equations

Some sufficient conditions are obtained by semigroups of operators and fixed point method.

To the best of our knowledge,under weaker Lipschitz conditions,there are few results on the existence and uniqueness of pseudo-almost automorphic mild solutions of stochastic differential equations.Motivated by the works[13,14],the main purpose of this paper is to study the composition theorem for pseudo-almost automorphic process under weaker Lipschitz conditions,and established the existence,uniqueness and stability of square-mean pseudo-almost periodic mild solutions for semilinear stochastic differential equations

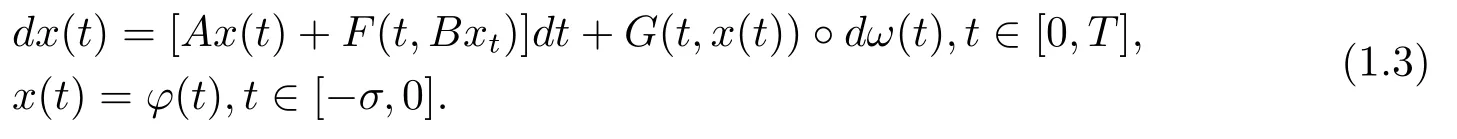
We assume thatAgenerates aC0semigroupT(t)satisfying‖T(t)‖ ≤Me−µtfor someM,µ＞0,andB:D(B)⊆X→Xis closed linear operator,whereXis a Banach space endowed with a norm‖·‖.F,Gare two appropriate functions to be specified later.

The rest of this paper is organized as follows.In Section 2,we recall some basic de finitions,lemmas and preliminary facts which will be useful throughout this paper.In Section 3,we establish a composition for pseudo-almost automorphic process.In Section 4,the existence and uniqueness of square-mean pseudo-almost periodic mild solutions of(1.3)are proved.

2 Preliminaries

Now let us state some de finitions and lemmas,which will be used in what follows.Let(Ω,F,P)be a probability space.For a Banach spaces(B,‖·‖),the notationL2(P,B)stands for the space of allB-valued random variablesxsuch that

De finition 2.1(see[12])A stochastic processx:R→L2(P,B)is said to be continuous,provided that,for anys∈R,

De finition 2.2(see[12])A stochastic processx:R→L2(P,B)is said to be stochastically bounded if there existsM＞0 such thatE‖x(t)‖2≤Mfor allt∈R.

LetSBC(R,L2(P,B))be the collection of all the stochastic bounded and continuous process.It is easy to see thatSBC(R,L2(P,B))is a Banach space.

De finition 2.3(see[18])A stochastic processx(t)∈SBC0(R,L2(P,B)),if

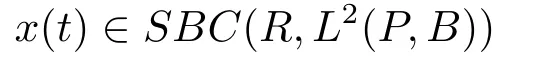
and

De finition 2.4(see[18])A stochastic processx:R→L2(P,B)is said to be squaremean almost automorphic,if for every sequence real numberthere exists a subsequence{sn}n∈Nand a stochastic processy:R→L2(P,B)such thatE‖x(t+sn)−y(t)‖2=0 andhold for eacht∈R.

Denote the collection of all square-mean almost automorphic stochastic process bySAA(R,L2(P,B)).By[18],we know thatSAA(R,L2(P,B)),‖·‖∞is a Banach space when it is equipped with normforx∈SAA(R,L2(P,B)).

De finition 2.5(see[18])A stochastically continuous processf:R→L2(P,B)is said to be square-mean pseudo-almost automorphic if it can be decomposed asf=g+ϕ,whereg∈SAA(R,L2(P,B))andϕ∈SBC0(R,L2(P,B)).

The collection of all the square-mean pseudo-almost automorphic processesf:R→L2(P,B)is denoted bySPAA(R,L2(P,B)).It is obvious that

De finition 2.6(see[17,19])A stochastically processf(t,x):R×L2(P,B)→L2(P,B),which is jointly continuous,is said to be square-mean pseudo-almost automorphic intfor anyx∈L2(P,B)if it can be decomposed asf=g+ϕ,where

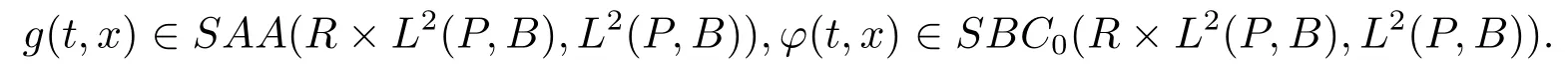
3 The Composition Theorem

In this section,we establish a composition theorem for stochastically square-mean pseudo-almost automorphic processes.Firstly,we prove some lemmas which are useful to obtain the composition theorem.

Lemma 3.1Assume thatf∈SBC0(R×L2(P,B),L2(P,B))satisfying that for anyε＞0,there existsδ＞0 and stochastic processL(t)∈SBC(R,L2(P,B))such that

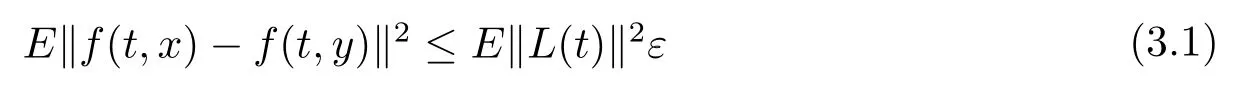
for allt∈Randx,y∈Kwith‖x−y‖＜δ,whereK⊂L2(P,B)is compact.Then

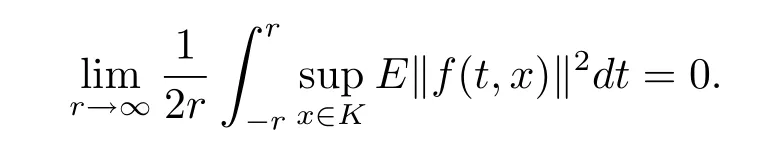
ProofFor any givenε ＞0,letδandL(t)be as in the assumptions.Takeε′=min{ε,δ}.SinceKis compact,there existsx1,···,xk∈Ksuch thatFrom the de finition ofSBC0(R×L2(P,B),L2(P,B)),for the aboveε＞0,there is constantT∗＞0 such that

For eachx∈K,there existsuix∈{u1,u2,···,uk}such that‖uix−u‖ ＜ ε′＜ δ.Then,from(3.1),we have

E‖f(t,x)‖2≤E‖f(t,x)−f(t,uix)‖2+E‖f(t,uix)‖2≤E‖L(t)‖2ε+E‖f(t,uix)‖2.

Then for eacht∈R,

By(3.2)and(3.3),for allr＞r∗,we obtain that

which implies that

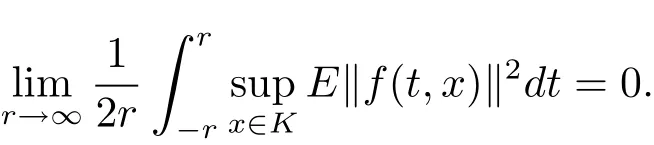
Theorem 3.2If the assumptions of Lemma 3.1 hold,

whereg∈SAA(R×L2(P,B),L2(P,B))andϕ∈SBC0(R×L2(P,B),L2(P,B)).Moreover,g(t,u)is uniformly continuous in any compact subsetK⊂L2(P,B)uniformly fort∈R.Then for each

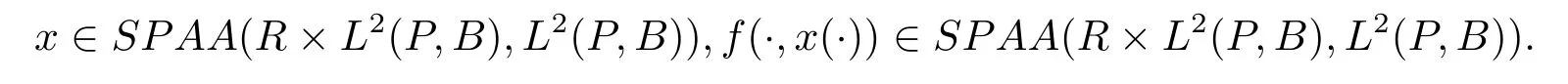
ProofLetx=α+β∈SPAA(R×L2(P,B),L2(P,B)),where

and

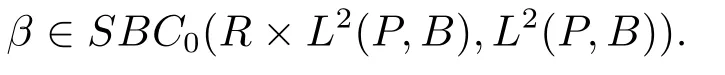
Set

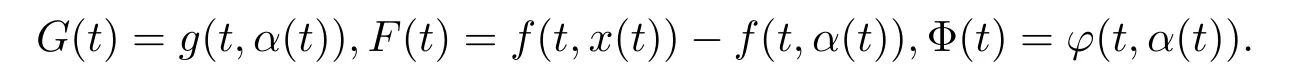
Thusf(t,x(t))=G(t)+F(t)+Φ(t).By[12]and the conditions,we have

From the de finition ofF,it is easy to see thatFis bounded,i.e.,for allt∈RthereM＞0 such thatE‖F(t)‖2≤M.For anyε＞0,and setMr,ε(f):={t∈[−r,r]:E‖f(t)‖2≥ ε},we have

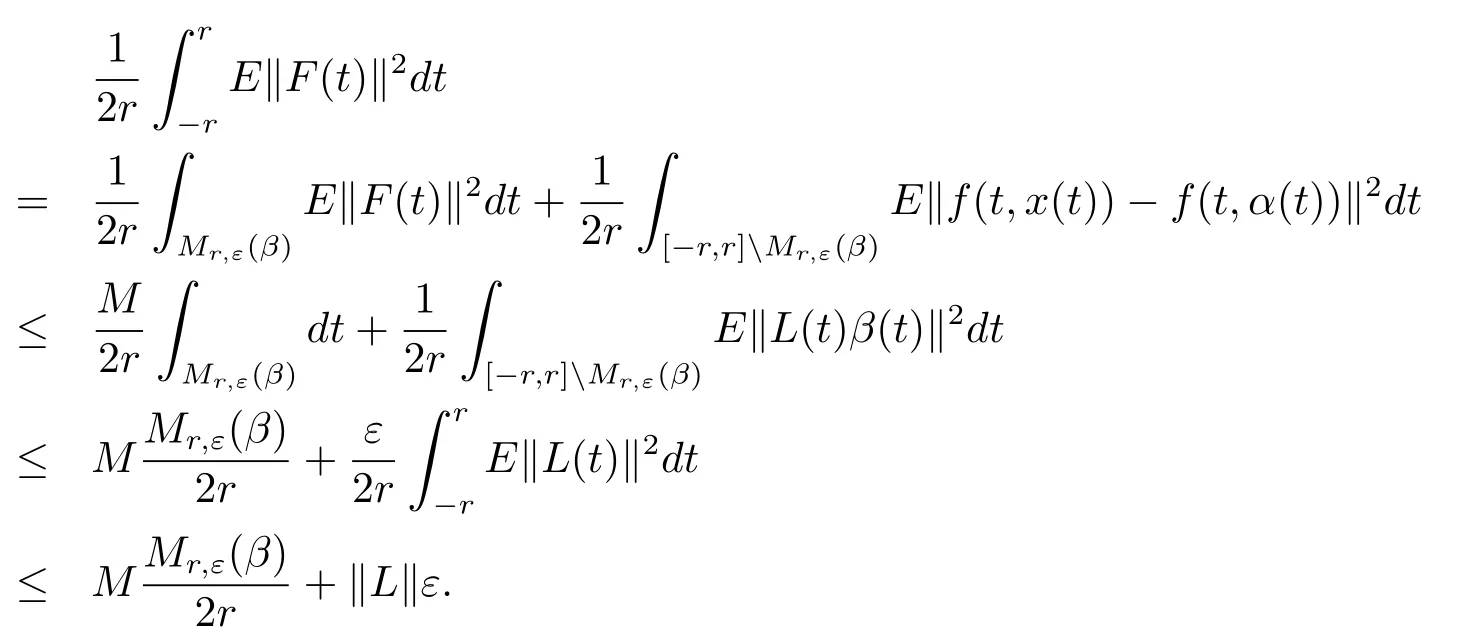
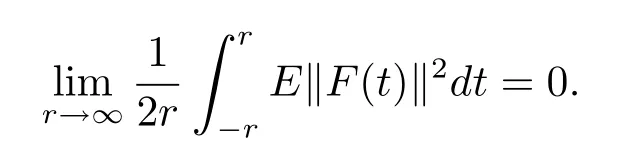
Therefore,F∈SBC0(R,L2(P,B)).Next,we show that Φ∈SBC0(R,L2(P,B)).LetK={α(t):t∈R}.ThenKis compact inL2(P,B).Sinceg(t,u)is uniformly continuous inKuniformly fort∈R,for anyε＞0,t∈R,andu,v∈Kwith‖u−v‖＜ δ,there exists a constantδ∈(0,ε)such thatE‖g(t,u)−g(t,v)‖2≤ ε.Therefore,it follows that

E‖ϕ(t,u)− ϕ(t,v)‖2≤E‖f(t,u)−f(t,v)‖2+E‖g(t,u)−g(t,v)‖2≤(E‖L(t)‖2+1)εfor allt∈Randu,v∈Kwith‖u−v‖＜ δ.From Lemma 3.1,we have

Since for eacht∈R,

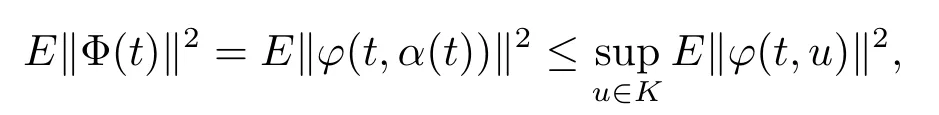
one can get

which implies that Φ∈SBC0(R,L2(P,B)).The proof is completed.

Corollary 3.3Iff∈SAA(R×L2(P,B),L2(P,B))and(3.1)holds,then for eachx∈SAA(R×L2(P,B),L2(P,B)),f(·,x(·))∈SAA(R×L2(P,B),L2(P,B)).

4 Application to the Composition Theorem

In this section,we study the existence and uniqueness of pseudo-almost automorphic solutions for the semilinear stochastic differential equation(1.3).

De finition 4.1A continuous stochastic processu:R→L2(P,B)is called a mild solution to eq.(1.3)on[−σ,T]if for allt∈[−σ,0],x(t)=ϕ(t)and for allt∈[0,T],

In order to establish the result,we need the following assumptions:

(H1)a generates aC0semigroupT(t)satisfying‖T(t)‖ ≤Me−µt,t＞0 for someM,µ ＞0;

(H2)the stochastic processesF:R×L2(P,B)→L2(P,B)andG:R×L2(P,B)→L2(P,B))are square-mean pseudo-almost automorphic;

(H3)the stochastic processesFandGsatisfy weaker Lipschitz conditions in second argument fort,that is there are two stochastic processesLF(t)andLG(t)such that,for anyx,y∈L2(P,B),

and

for allt∈R.

Theorem 4.2Assume that(H1),(H2)and(H3)hold.Then equation(1.3)has a unique square-mean pseudo-almost automorphic mild solution whenever

ProofLet us de fine the operatorPonSPAA(R×L2(P,B),L2(P,B))by

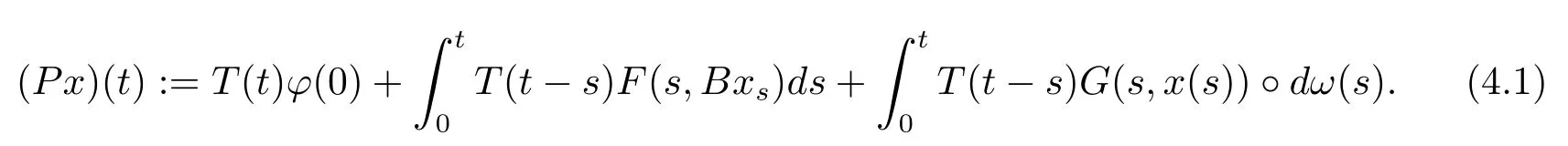
By Theorem 3.2 andBis closed linear operator,for each

we have

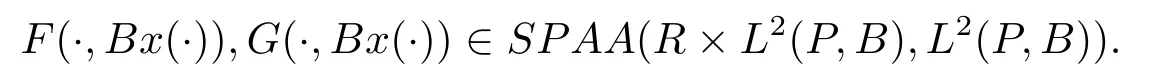
Thanks to[15],one can easily show thatPmapsSPAA(R×L2(P,B),L2(P,B))into itself.Next,we prove thatPis a contraction mapping and has a unique fixed point,

Since(a−b)2≤2a2+2b2,one can get

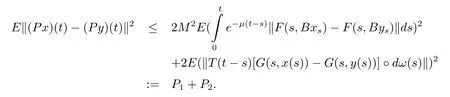
First,we evaluateP1as follows:

ForP2,one can obtain

Therefore,byP1andP2,it follows that

By(4.2),we have that

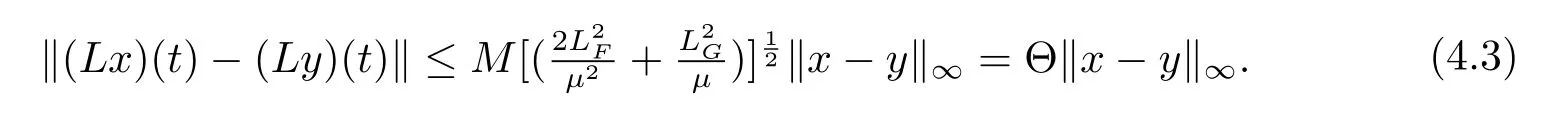
Since Θ＜1,from(3.5),we obtain thatPis a contraction mapping.Therefore,Phas a unique fixed pointx(t),which clearly is the unique square-mean pseudo-almost automorphic mild solution to eq.(1.3).The proof is completed.

Corollary 4.3If(H1),(H2)and(H3)hold withLF(t)=LFandLG(t)=LG.Then equation(1.3)has a unique square-mean pseudo-almost automorphic mild solution whenever

5 Conclusion

In this paper,we study a composition theorem for pseudo-almost automorphic stochastic process is established under a weaker Lipschitz condition,the result improves some known results,such as[12,15,18].So the result and its application are valuable.However,there are still many interesting and challenging questions that need to be studied for eq.(1.3).For example,whether the stability of system(1.3)can be considered by constructing an appropriate Lyapunov function?We will leave this for future work.

[2]Fink A M.Almost periodic differential equations[M].Berlin:Springer-Verlag,1974.

[2]Zhang C Y.Pseudo almost periodic solutions of some differential equations[J].J.Math.Anal.Appl.,1994,151:62–76.

[3]He M X,Chen F D,Li Z.Almost periodic solution of an impulse differential equation model of plankton allelopathy[J].Nonl.Anal.,2010,11:2296–2301.

[4]Li Z,Chen F.Almost periodic solutions of a discrete almost periodic logistic equation[J].Math.Comput.Model.,2009,50:254–259.

[5]Wang Y H,Xia Y H.The existence of almost periodic solutions of a certain nonlinear system[J].Commun.Nonl.Sci.Numer.Simulat.,2011,16:1060–1072.

[6]Abbas S,Bahuguna D.Almost periodic solutions of neutral functional differential equations[J].Comput.Math.Appl.,2008,11:2539–2601.

[7]Zhou H,Zhou Z.Weighted pseudo-almost periodic solutions of neutral integral and differential equations[J].J.Math.Res.,2011,4:74–79.

[8]Xiao T J,et.al.Pseudo almost automorphic mlid solutions to nonautonomous differential equations and applications[J].Nonl.Anal.,2009,70:4709–4085.

[9]Liu J H,Song X Q.Almost automorphic and weighted pseudo almsot automorphic solutions of semilinar evolution equations[J].J.Funct.Anal.,2010,258:196–207.

[10]Zhao Z H,Chang Y K,Li W S.Asymptotically almost periodic,almost periodic and pseudo-almost periodic mild solutions for neutral differential equations[J].Nonl.Anal.,2010,11:3037–3044.

[11]Tudor C,Tudor M.Pseudo almost periodic solutions of some stochastic differential equations[J].J.Math.Rep.,1999,51:305–314.

[12]Bezandrt P,Diagana T.Existence of almsot periodic solutions to some stochastic differential equations[J].Appl.Anal.,2007,117:1–10.

[13]Fu M M,Liu Z X.Square-mean almsot automorphic solutions for some stochastic differential equations[J].Proc.Amer.Math.Soc.,2010,138:3689–3701.

[14]Liu P,Li Y.Positive periodic solutions of in finite delay functional differential equations depending on a parameter[J].Appl.Math.Comput.,2004,150:159–168.

[15]Cao J F,et al.On almost periodic mild solutions for stochastic functional differential eqations[J].Nonl.Anal.,2012,13:275–286.

[16]Jiang D Q,O’Regan D,Agarwal R P,Xu X J.On the numbers of positive periodic solutions of functional differential equations and populationn models[J].Math.Models Meth.Appl.Sci.,2005,15:555–573.

[17]Hale J K.Theory of functional differential equations[M].New York:Springer-Verlag,1977.

[18]Sakthivel R,et al.Existence of pseudo almost automorphic mild solutions to stochastic fractional differential equations[J].Nonl.Anal.,2012,75:3339–3347.

[19]Smart D R.Fixed points theorems[M].Cambridge:Cambridge Univ.Press,1980.

伪概自首随机过程分解及应用

周 辉1,周宗福2,乔宗敏1
(1.合肥师范学院数学与统计学院,安徽合肥 230061)
(2.安徽大学数学科学学院,安徽合肥 230039)

在较弱Lipschitz条件下,本文建立伪概自守随机过程分解定理,该定理推广了已知结果.利用所建立理论的性质,本文获得了一类随机微分方程的伪概自守弱解的存在唯一性条件.

伪概自守;分解;均方;弱解

O174.23

42A75;43A60

A

0255-7797(2017)06-1134-09

1 Introduction

Almost periodic functions were introduced in[1],and Zhang[2]introduced the concept of pseudo-almost periodic functions,which are a natural generalization of almost periodic functions.The investigation of the existence of almost periodic,pseudo-almost periodic,almost automorphic and pseudo-almost automorphic solutions is one of the most interesting topics in the qualitative theory of differential equations due to their applications[3–10]in physics,biology,dynamical systems and so on.Recently,in[11],the concept of square-mean almost periodicity was introduced and studied.

As we all know,most real problems in areal life situation are basically modeled by stochastic equations rather than deterministic,because a natural extension of a deterministic model is stochastic model.Bezandry et al.[12]studied the existence of almost periodic or pseudo almost periodic solutions to stochastic functional differential equations.However,almost automorphic functions are a natural generalization of almost periodic functions.Fu and Liu[13]introduced a new notion of a square-mean almost automorphic stochastic process and the authors studied the existence and uniqueness of square-mean almost automorphic mild solutions to a class of automorphic differential equations.

date:2014-03-26Accepted date:2014-05-19

Supported by the National Science Foundation of Anhui Province(1608085MA12);Hefei Normal University Young Foundation(2015QN19).

Biography:Zhou Hui(1986–),male,born at Lixin,Anhui,major in the theory of functional differential equations and stochastics differential equations.