动剪切模量阻尼比试验误差及对地震动影响风险评价
2017-11-06李晓飞汪云龙
李晓飞,汪云龙,孙 锐,李 波
(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室,哈尔滨 150080;2. 滨州学院 建筑工程学院,山东 滨州 256600)
动剪切模量阻尼比试验误差及对地震动影响风险评价
李晓飞1,2,汪云龙1,孙 锐1,李 波2
(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室,哈尔滨 150080;2. 滨州学院 建筑工程学院,山东 滨州 256600)
为认识动剪切模量比和阻尼比非线性试验误差及其对地震动的影响,采用试验和数值模拟手段,研究了动剪切模量比和阻尼比试验误差并提出其概率分布特征,以及这一误差对土层地震动计算结果的影响和规律,给出了其对地震动影响的风险水平。设计了离散性最大和最小的两种代表性试验组,通过单台共振柱仪试验给出了试验误差的概率统计指标。同时设计不同类别场地和不同地震波输入,完成风险分析。结果表明:两种类别组的动剪切模量比和阻尼比试验数据均服从正态分布,二者试验均值接近,但变异系数相差5倍左右;动剪切模量比和阻尼比试验误差对地震动计算结果有重要影响,影响程度随试验误差增大、场地变软和地震强度增加而增大,其中试验误差和场地类别起主要作用;以对场地地震动产生不可忽视影响为阈值,初级技术人员动剪切模量和阻尼比的试验误差对中硬场地的风险水平为35%,对软场地则为50%;就一般情况,应强化共振柱试验技术规程,提高试验人员技术水平,否则会对工程结构的地震动输入估计造成很大风险。
动剪切模量比和阻尼比;试验误差;概率分布;地震动;风险评价
基于可靠度和风险分析的设计理念已逐渐成为工程结构抗震设计和工程安全设计的主流思想。岩土材料是自然历史的产物,而目前岩土参数基本采用试验方法得到。因此,土性参数的不确定性主要来自于两方面:一是内在因素,即土体本身固有变异性的影响;二是外在因素的影响,如试验技术、分析方法等。对于土体静力学指标,土性参数的不确定性已经有一些研究成果[1-3]。同时,土体作为地震波传播的介质,动力性能直接影响结构的安全,其动力参数的估计也直接影响工程造价[4]。土的动剪切模量比和阻尼比是土动力特性两个首要参数,而共振柱因原理可靠、分析方法相对简单,已成为目前获取土的动剪切模量比和阻尼比相对理想的仪器,也是国家标准《工程场地地震安全性评价》(GB 17741—2005)[5]中规定使用的设备。对任何一个可以重复测量的科学数据,其误差水平、置信区间都是必须回答的问题,但迄今为止共振柱试验误差的研究成果尚少。祝龙根等[6]采用统一的标准砂为样本,对不同类型共振柱仪器得到的试验数据进行了对比研究,结果表明,不同类型共振柱仪试验得到的剪切模量值有一定的离散性,在我国开创了这方面研究的先河。除了不同类型共振柱仪外,单一类型的共振柱试验也会存在试验误差,但目前这方面的研究尚无成果发表。
土层地震动计算是工程抗震设计的基础,土层地震动计算中土的动剪切模量比和阻尼比是地震小区划、重大工程抗震设计和地震安全性评价工作中必不可少的分析参数[7-11]。土的动剪切模量比和阻尼比对设计地震动影响问题,已经有一些研究成果[12-15],结果表明,对地震动计算结果来说动剪切模量比是一个比剪切波速还要敏感的参数。但是,由于动剪切模量比和阻尼比测试误差定量结果尚少,以往其对地震动影响只能采用假定的参数离散程度的方式进行研究,这两个重要参数试验误差对地震动计算的真实影响程度不得而知。由于动剪切模量比和阻尼比试验误差的概率分布特征未知,因此引起地震动计算结果的风险程度也成为未知数。从工程抗震设计角度,由于目前还没有建立动剪切模量比和阻尼比试验误差与设计地震动风险水平之间的关系,一些专家学者对动剪切模量比和阻尼比试验结果的可靠性心存疑虑,反之也无法从对设计地震动影响角度评价现有共振柱试验精度和技术水平,也影响了相关标准的制订和试验技术的改进。
本文采用共振柱试验,研究动剪切模量比和阻尼比试验误差问题,给出测试误差分布形态和基本规律,提出概率统计指标;针对不同类别场地与不同地震动输入,研究动剪切模量比和阻尼比试验误差对地震动计算结果的影响特征和规律,给出现有试验水平下试验误差对地震动计算结果影响的风险评价。目的是把握现有共振柱试验水平,掌握该水平下地震动计算误差的风险,为制定共振柱试验标准提供依据,为地震动和工程结构抗震风险分析提供基础。
1 动剪切模量比和阻尼比试验及分析
1.1试验设计
试验采用中国地震局工程力学研究所研制的我国第一台具有自主知识产权的GZ-1改进型仪器,主要技术指标见表1。该仪器为固定-自由端型,其可靠性已经得到检验。
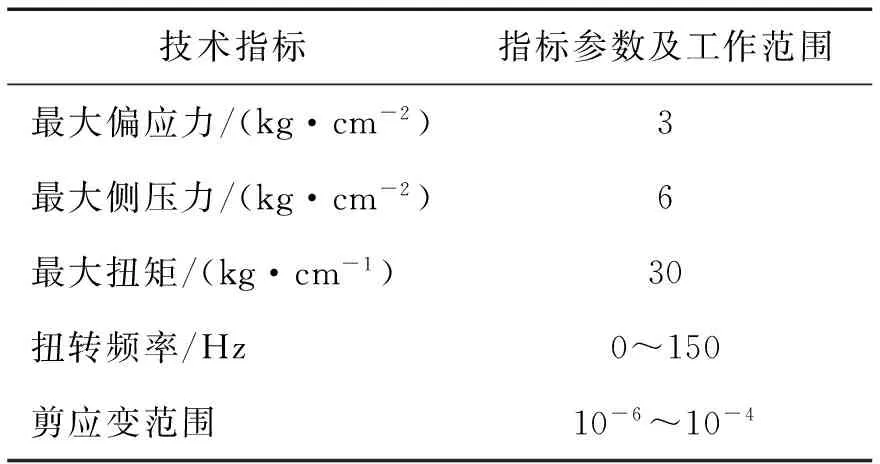
表1 GZ-1型共振柱技术指标Tab.1 Technical indexes of GZ-1 resonant column
试验所用土为福建标准砂,其最大干密度为1.679 g/cm3,最小干密度为1.464 g/cm3,不均匀系数Cu=1.44,曲率系数Cc=0.92,比重2.644 g/cm3。试样尺寸为Φ39.1 mm×80 mm,所有土样的固结压力均采用100 kPa。
本文针对初级组和高级组两种典型工况研究动剪切模量比和阻尼比的共振柱试验误差问题。
初级组,试验由10名经过培训的科技人员完成,代表着初等级别的试验结果;高级组,试验由1人完成,为具有丰富经验的专业试验人员,代表着高等级别的试验结果。初级组和高级组,代表着试验群体的两种极端情况。从风险分析角度,本试验分组设计代表了两种典型情况;从对地震动计算结果的影响角度,可提供风险最大和风险最小的评价结果。
初级组中每个试验人员分别进行4次试验,即得到试验数据40组;高级组中试验人员分别进行40次试验。每人(次)试验中,砂土均需要重新制样,制样方法按国标《土工试验规程》(SL 237—1999)[16]进行。试验过程分为试样的制备和装样两部分,大致如下:
(1) 重塑砂土土样的制备,根据相对密度,计算出每个土样所需要干砂的质量。分四层均匀装入三片模中,为保证试样成型良好,每片膜上都要摸油,通过锤击使每层土高度为20 mm。每层锤击到指定高度时都要进行刮毛,每层干砂中加入5 ml水。
(2) 将做好的土样,拆下三片模,通过套筒套上橡皮膜,然后将试样安装在共振柱上,试样上端与下端都要通过橡皮套与仪器绑结实,保证不漏气。盖上盖子,加上100 kPa围压,均等固结6 h。
动剪切模量比和阻尼比与剪应变是非线性关系。共振柱试验得到的是小中应变下的结果,对中大应变下的曲线采用公认的双曲线模型得到,双曲线模型参数由试验点回归确定。确定8个典型剪应变5×10-6、1×10-5、5×10-5、1×10-4、5×10-4、1×10-3、5×10-3和1×10-2下的动剪切模量比和阻尼比。
1.2试验结果及误差分布形态
初级组和高级组的动剪切模量比和阻尼比试验结果如图1所示。
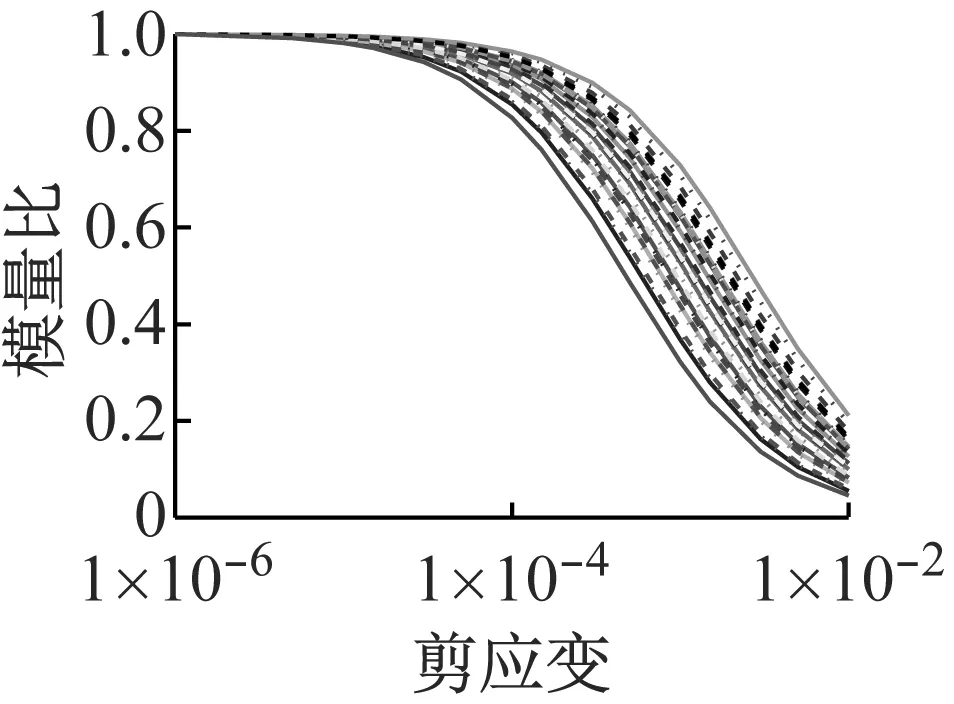
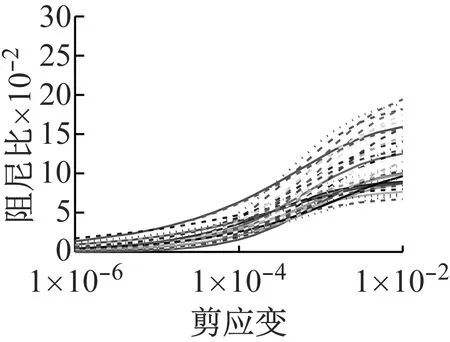
(a) 初级组
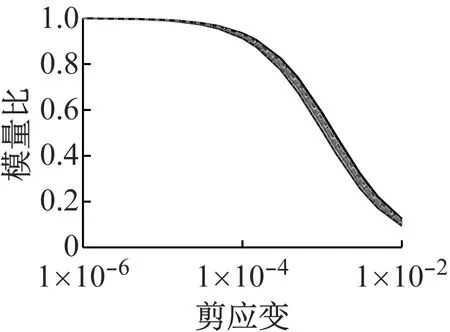
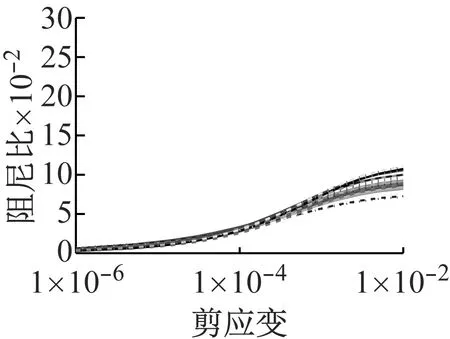
(b) 高级组图1 动剪切模量比和阻尼比试验结果Fig.1 Test results of shear modulus ratios and damping ratios
从试验结果看,高级组的试验结果很正常,但初级组个别曲线离散较大,特别是阻尼比的情况。考虑到以往经验中,阻尼比试验的稳定性一般要小于模量比试验,因此本文没有将阻尼中离散较大的试验点作为异常点去掉,仍然纳入到统计数据中。
根据统计学中的异常值检验经验方法[17],上述各个曲线超过97%的试验结果落在均值2倍标准差范围内,超过95%的基准值要求,故试验结果可靠可用。
采用频数直方图法确定8个典型剪应变下动剪切模量比和阻尼比的分布形态。初级组和高级组在剪应变为10-4时的剪切模量比和阻尼比的频数直方图如图2所示,从图中可见,动剪切模量比和阻尼比在剪应变为10-4时均服从正态分布,其他剪应变下的结果类同。采用统计学权威软件SPSS对剪应变10-4时的剪切模量比和阻尼比进行正态性检验,给出采用Shapiro-Wilk检验的P值,结果在0.36~0.65,远大于阈值0.05,数据服从正态分布。其他剪应变下的结果类同。

(a) 初级组

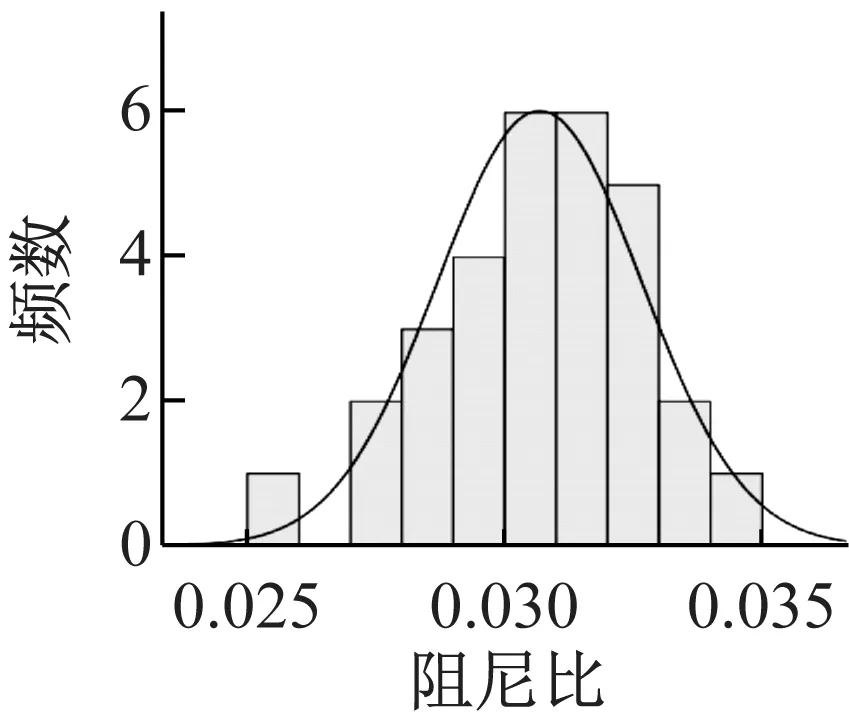
(b) 高级组图2 剪应变为10-4时剪切模量比和阻尼比的频数分布图Fig.2 Frequency distribution and test results for shear modulus ratio and damping ratio at strain of 10-4
1.3试验误差离散性指标
本文采用统计分析方法,以最大值、最小值、均值、标准差、一倍标准差、变异系数以及不同概率水准等指标来描述土样在8个典型剪应变下动剪切模量比和阻尼比的离散性。对于图1的试验结果,针对8个典型剪应变,计算出初级组和高级组的动剪切模量比和阻尼比的离散性指标,结果见表2和表3。
由表2和表3可知,初级组和高级组的动剪切模量比和阻尼比试验都有离散性,但初级组动剪切模量比和阻尼比试验的离散性指标远大于高级组的指标。模量比标准差的最大值均出现在剪应变10-4~10-3内,此范围恰是土层地震反应分析计算中动剪切模量比最常出现的区间。随着剪应变的增长,模量比的变异系数也呈现增长趋势,表明应变较小时动剪切模量比的离散性小,应变大时动剪切模量比的离散性明显增大;阻尼比的变异系数随着剪应变的增长呈现下降趋势,表明小应变时阻尼比的离散性大,应变大时阻尼比的离散性小。
就均值而言,无论动剪切模量比还是阻尼比,初级组与高级组试验结果都十分接近。
1.4初级组与高级组试验离散性的对比
将表2和表3中动剪切模量比和阻尼比的一倍标准差曲线、外包线(最大值和最小值)曲线及其方程以及均值曲线示于图3。从图3看出,初级组动剪切模量比和阻尼比的外包线方程相差很大,而高级组的方程相差很小,说明高级组和初级组试验精度差异显著。从图3也可看出,初级组试验的一倍标准差与均值、外包线与一倍标准差之间均差别明显,而高级组差别则很小,表明初级组试验离散性明显大于高级组,说明高级组的试验误差很小,也说明试验人员因素、试验技术水平对试验结果可靠性影响很大。
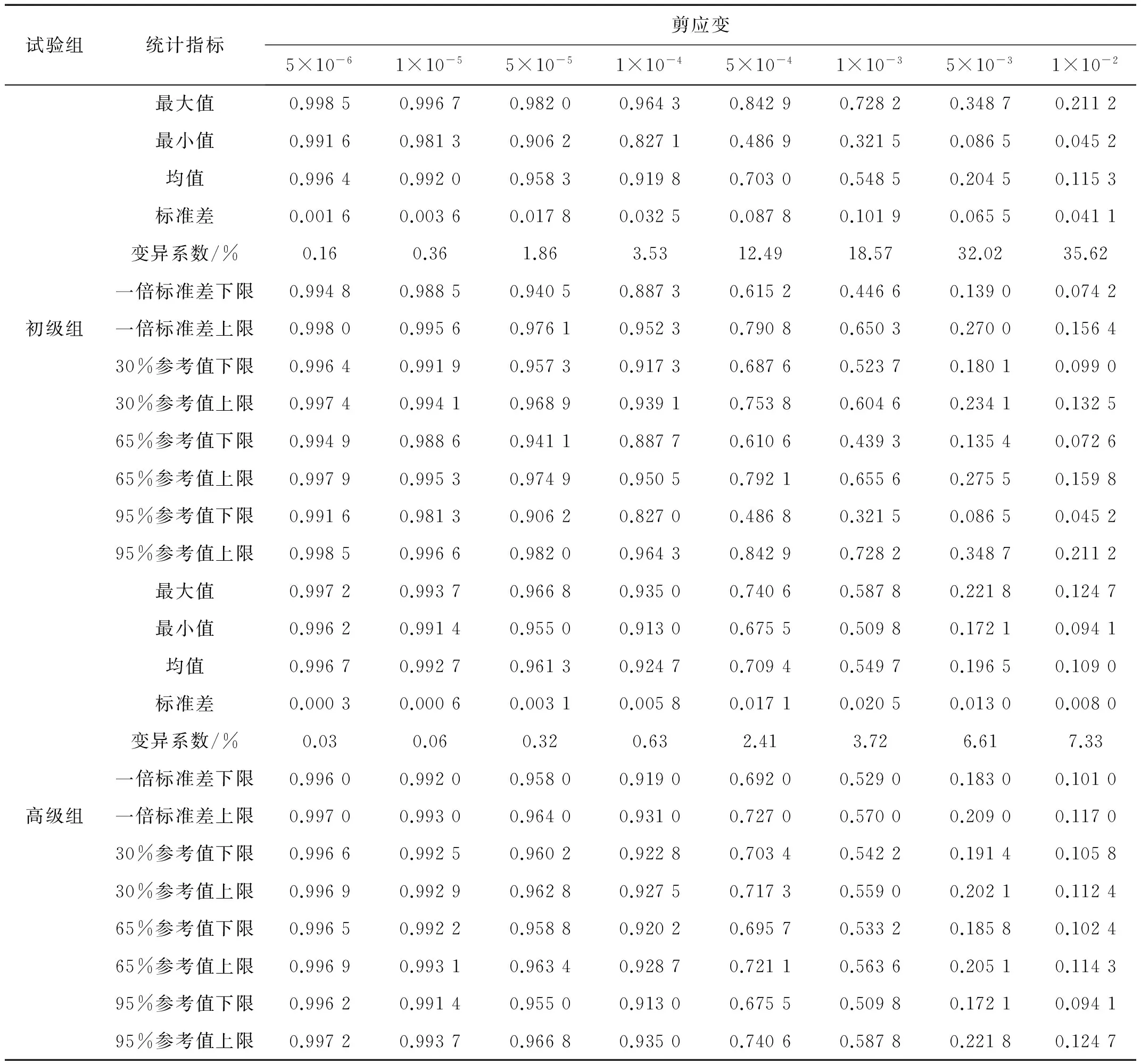
表2 模量比试验误差概率分布特征Tab.2 Probability distribution of modulus ratio test error
同时,由表2和表3也可看出,就模量比而言,初级组的误差是高级组的5倍左右,且随剪应变波动较小;而初级组阻尼比误差是高级组的4.5倍左右,且随剪应变波动较大,剪应变为10-4时最大。这些结果表明,不同人员、不同试验水平对土的动剪切模量比和阻尼比试验误差影响非常显著。
2 动剪切模量比和阻尼比试验误差对地震动影响分析
2.1计算模型
通过概率分析方法,算出动剪切模量比和阻尼比不同概率水准的上下限,研究不同概率水准动剪切模量比和阻尼比对峰值加速度、加速度反应谱的影响。选取硬、中硬和软场地(即一、二、三类场地)为研究对象,场地计算模型信息列入表4。采用一维土层等效线性化程序SHAKE2000进行计算。
2.2输入地震动
确定地震动输入是等效线性化土层地震反应分析的一项重要工作。本文选用了3条地震波:El Centro波、AKTH19波和KSRH09波,其中El Centro波代表频率成分均匀的地震波,AKTH19波代表长周期成分占优的地震波,KSRH09波代表短周期成分占优的地震波;三条地震波反应谱的卓越周期分别为:El Centro地震波Ts=0.25 s,AKTH19地震波Ts=2.15 s,KSRH地震波Ts=0.14 s;分别采用三种输入地震动峰值0.1g、0.2g和0.4g;输入加速度时程见图4。
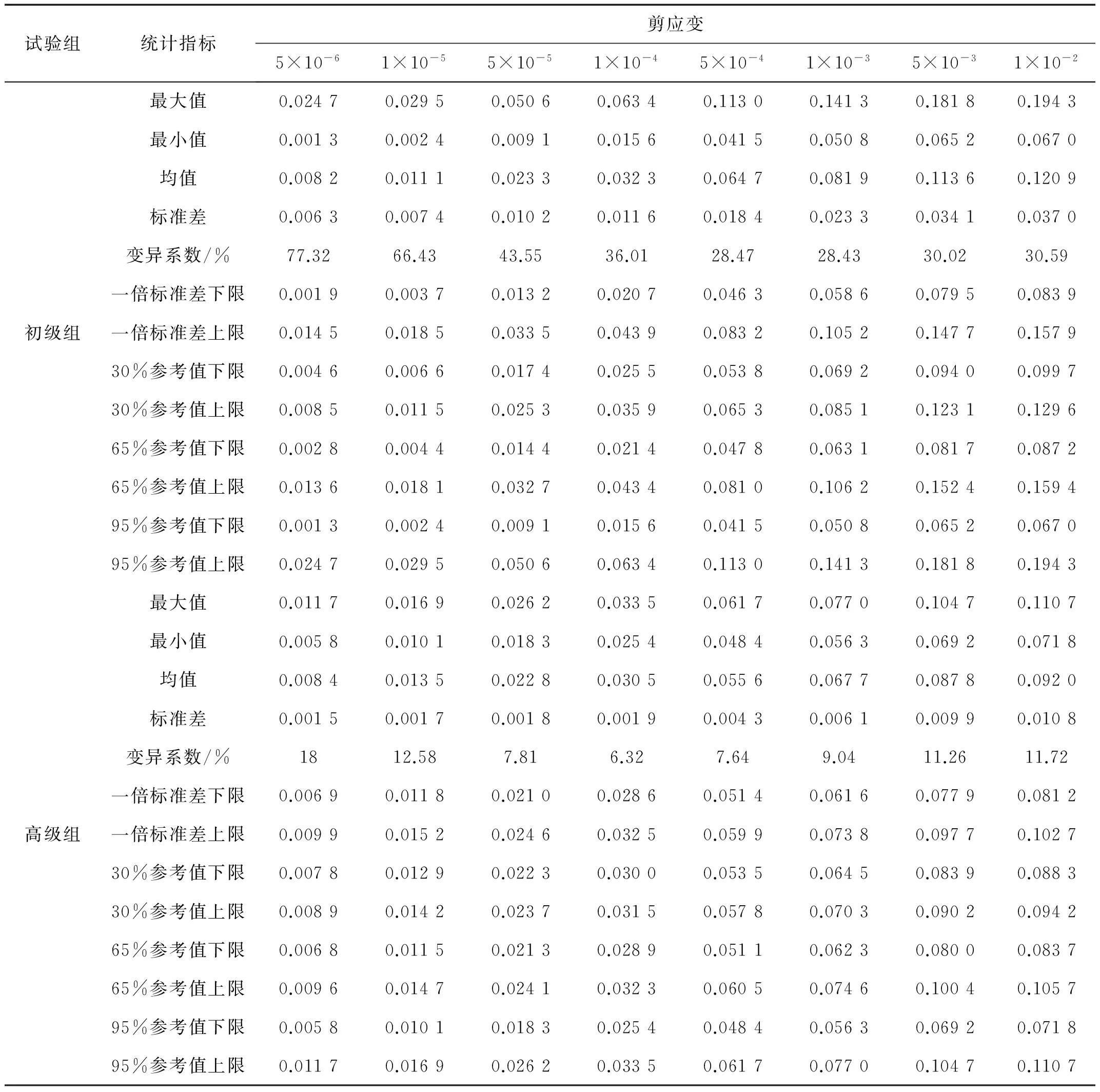
表3 阻尼比试验误差概率分布特征Tab.3 Probability distribution of damping ratio test error
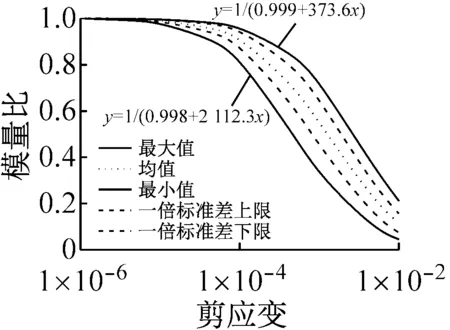
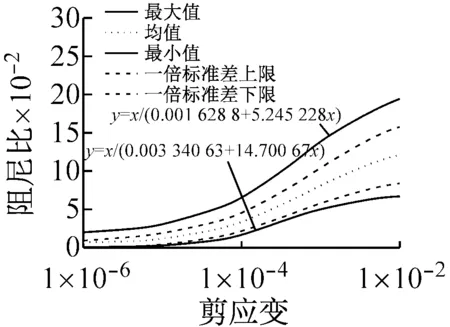
(a) 初级组
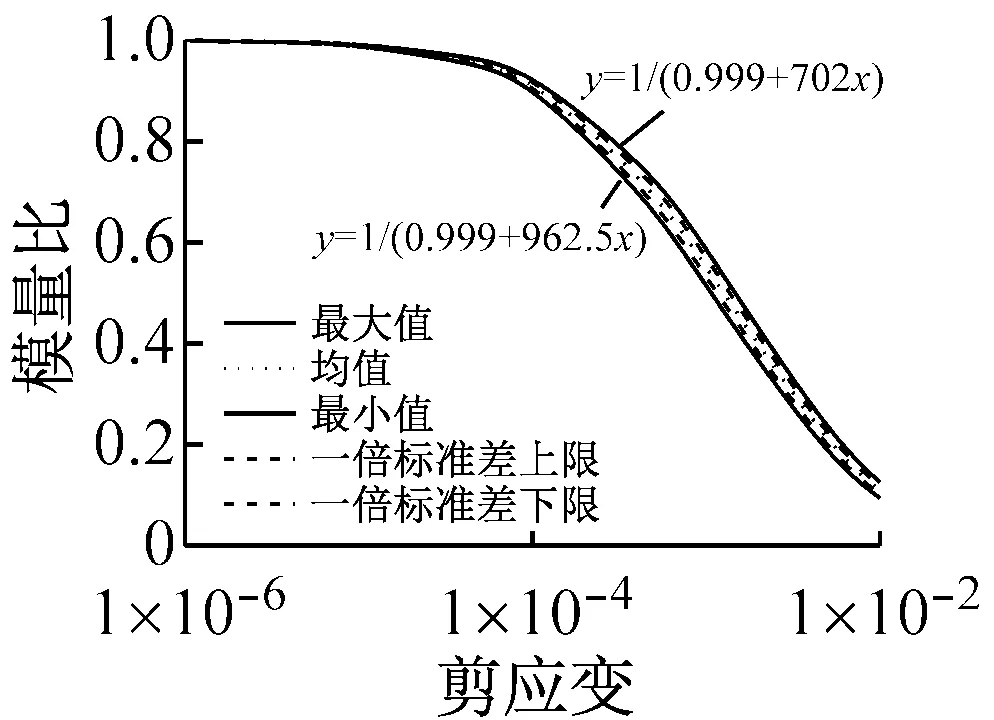
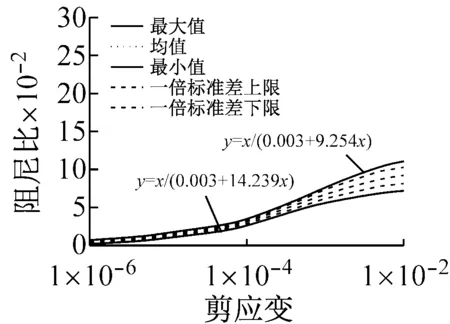
(b) 高级组图3 动剪切模量比和阻尼比均值、一倍标准差和外包线曲线Fig.3 Mean values, standard deviation and envelopes curves for dynamic shear modulus ratio and damping ratio
2.3土的动力非线性参数
为研究动剪切模量比和阻尼比的试验误差对地震动的影响,在计算中,动剪切模量比和阻尼比按照程序计算出的不同概率水准的上下限进行取值。研究动剪切模量比对地震动的影响时,动剪切模量比采用了7组非线性指标,分别为95%上限、65%上限、30%上限、均值、30%下限、65%下限和95%下限,相应的阻尼比均取均值情况;当研究阻尼比对地震动的影响时,阻尼比取7组非线性指标,相应的动剪切模量比均取均值情况。具体值见表2和表3。

表4 场地计算模型Tab.4 Calculation models of sites
2.4动剪切模量比误差影响
2.4.1 动剪切模量比误差对PGA影响的风险分析
本文以动剪切模量比取均值时SHAKE2000计算的地表加速度峰值为标准,计算不同概率水准动剪切模量比下的加速度峰值与其之间的相对误差,以此来分析动剪切模量比试验误差对地震动的影响。本文认为加速度峰值相对误差小于20%时,在工程上可以接受,此时对地震动的影响可以忽略,反之不可忽略。按最不利原则对结果进行分析,即同一概率水准下上限和下限参数进行计算,取相对误差最大的情况。初级组和高级组不同概率水准动剪切模量比条件下的加速度峰值与非线性取均值时的加速度峰值之间的相对误差见表5。
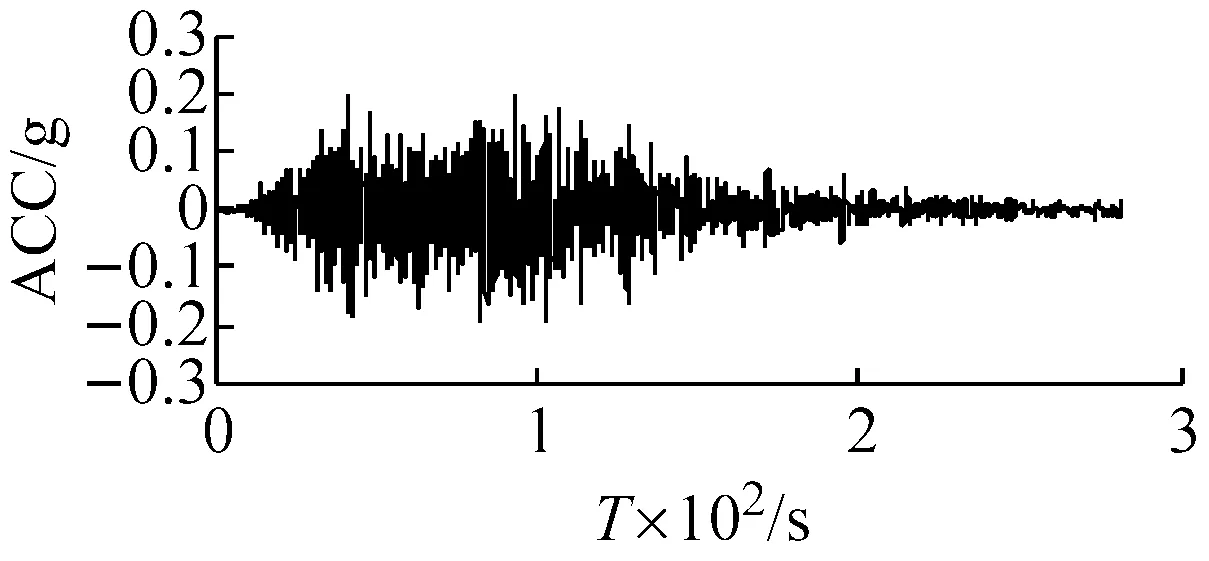
(a) AKTH19波
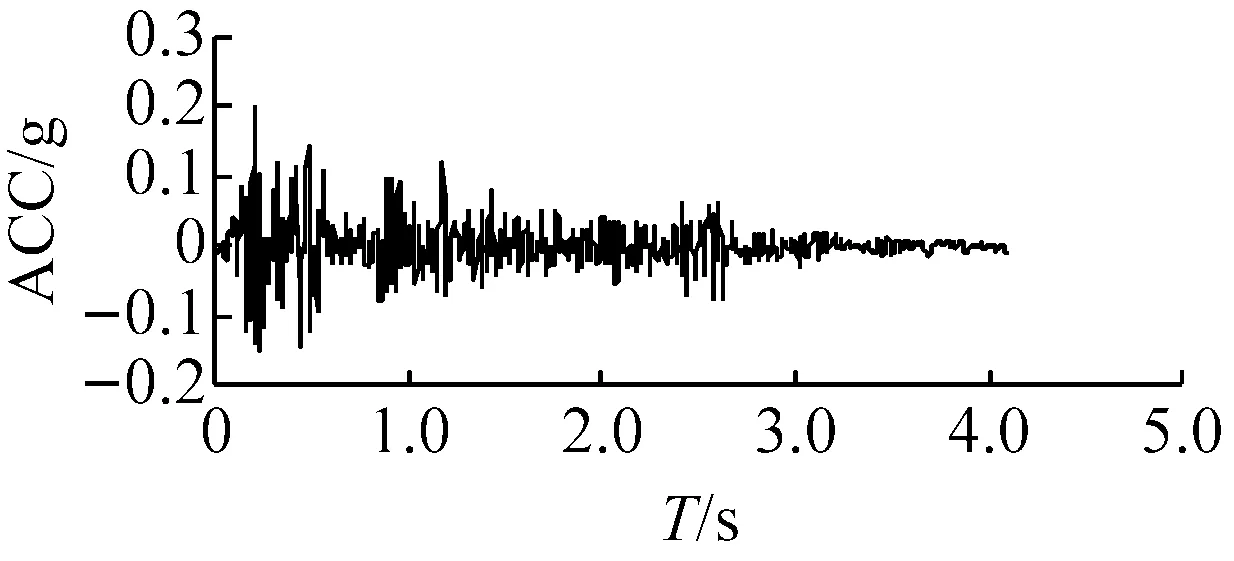
(b) Elcentro波
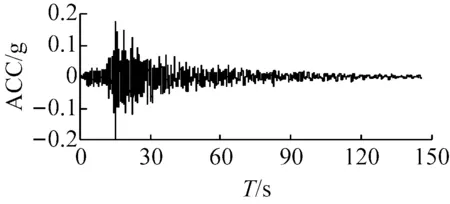
(c) KSRH09波图4 输入加速度时程曲线(PGA=0.2g)Fig.4 Input acceleration time-history curves (PGA=0.2g)
由表5可知,对于初级组,在硬场地中加速度峰值的相对误差均在10%以内,动剪切模量比试验误差对峰值加速度的影响可以忽略。中硬场地中,65%概率范围内动剪切模量比对峰值加速度的影响可以忽略,超过65%概率范围的动剪切模量比对峰值加速度的影响不可忽略。软土场地中,50%概率范围内动剪切模量比对峰值加速度的影响可以忽略,超过50%概率范围的动剪切模量比对峰值加速度的影响不可忽略。
对于高级组,硬场地和中硬场地中,动剪切模量比试验误差对峰值加速度的影响可以忽略。软场地中,95%概率范围内动剪切模量比试验误差对峰值加速度的影响可以忽略,超过95%概率范围的动剪切模量比试验误差对峰值加速度的影响不可以忽略。
通过提供优惠政策,使贫困县获得特殊的发展条件以减轻或部分抵消其自然条件和发展落后施加于地方发展的限制,在局部形成政策优势,在不同阶段给予贫困地区不同的优惠政策,如土地政策、进出口政策、减免农业税,出让部分中央政府和地方政府的收益给贫困地区和贫困户,或者改善其发展环境、提高其竞争和发展能力,或者直接增加其福祉。
综上所述,以对场地地震动产生不可忽视影响为阈值,就初级技术人员的试验,其动剪切模量比的试验误差风险对硬场地基本可以忽略,对中硬场地的风险水平为35%,对软场地则为50%。技术熟练人员的试验,对硬、中硬场地,其动剪切模量比的试验误差风险水平接近0,对软场地有5%的风险。
2.4.2 动剪切模量比误差对反应谱影响的风险分析
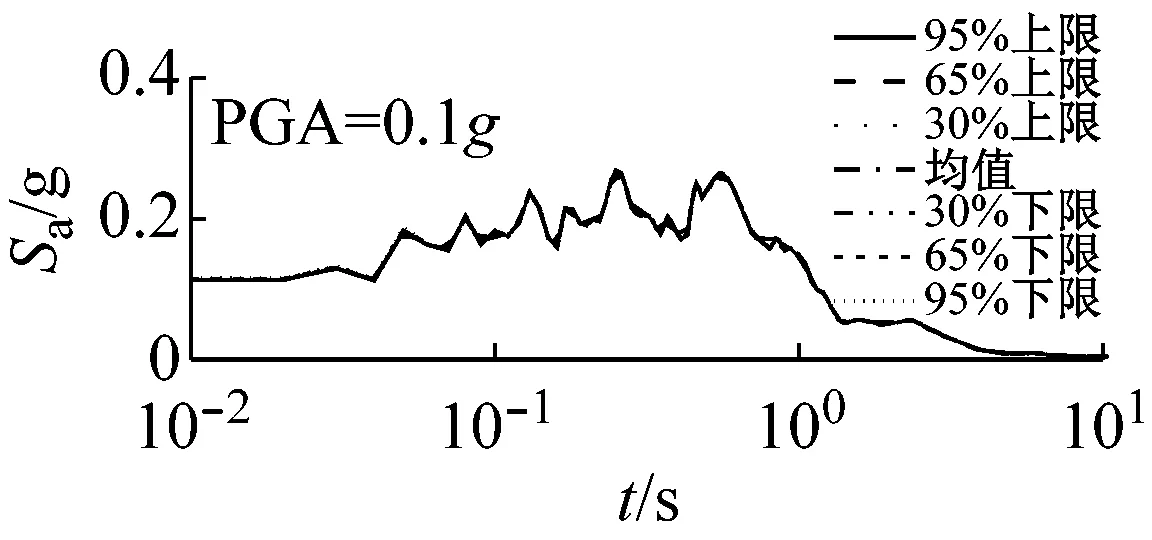
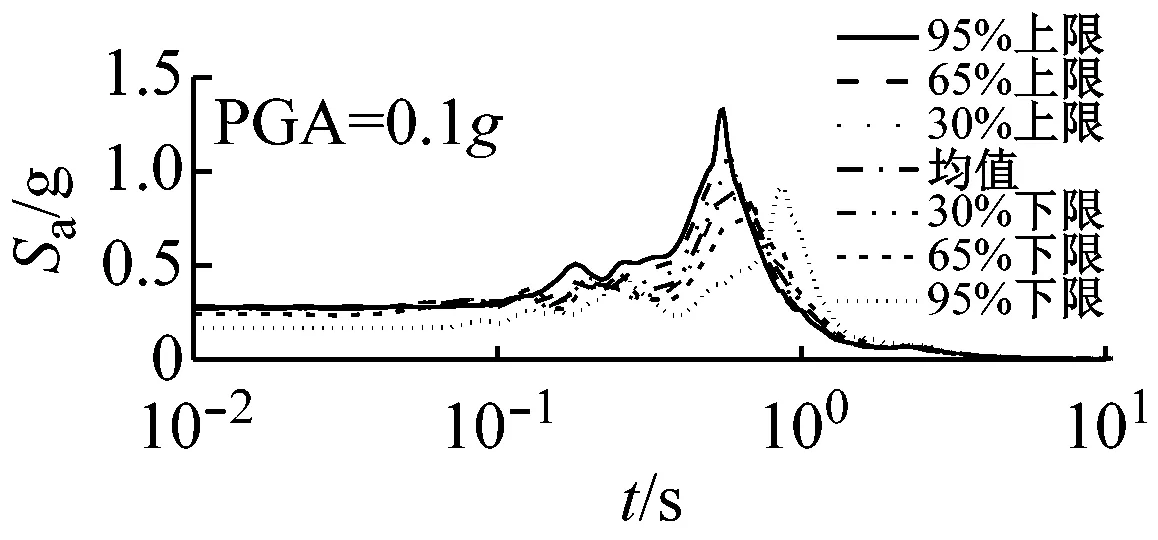
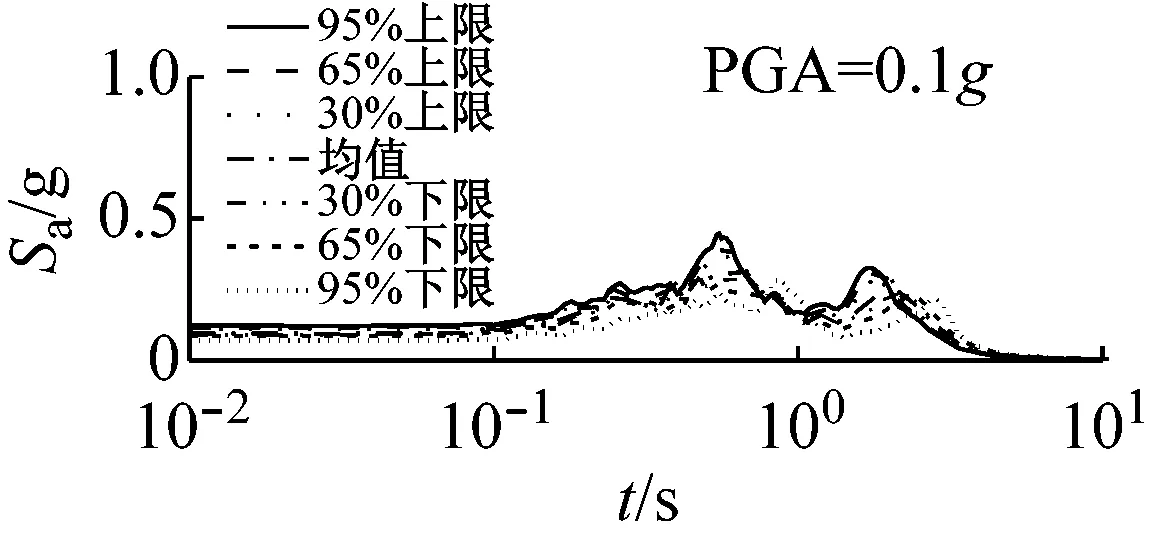
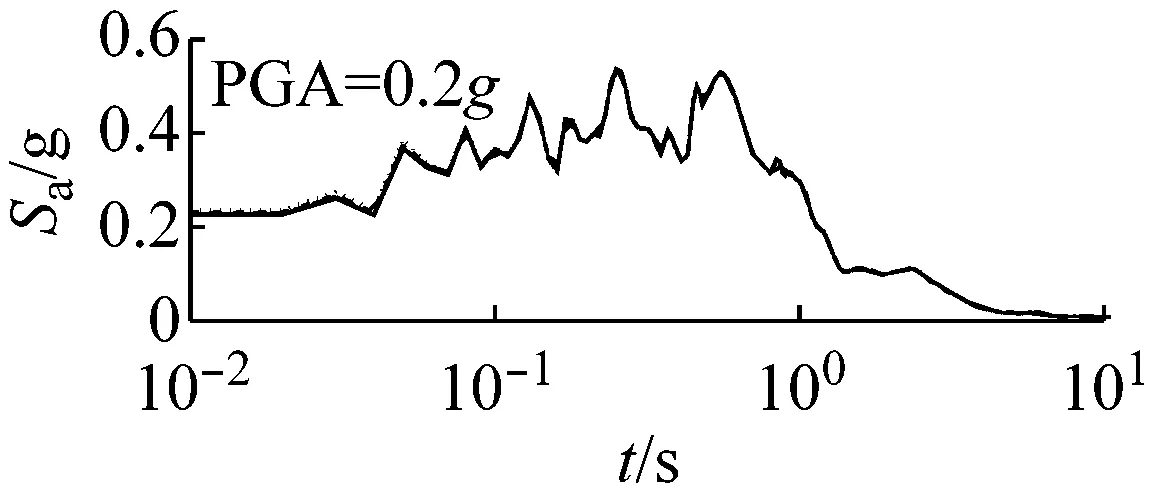
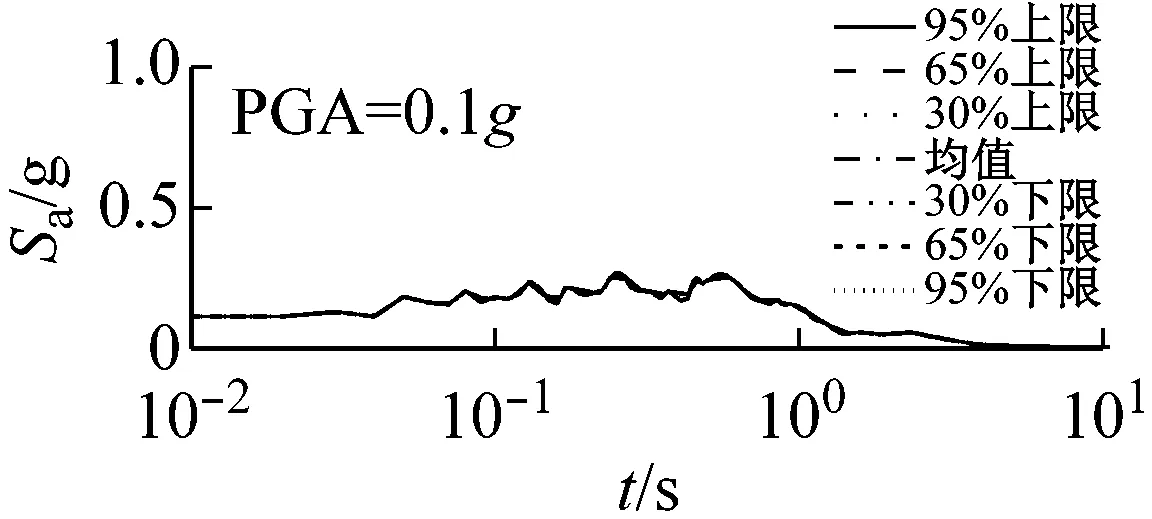
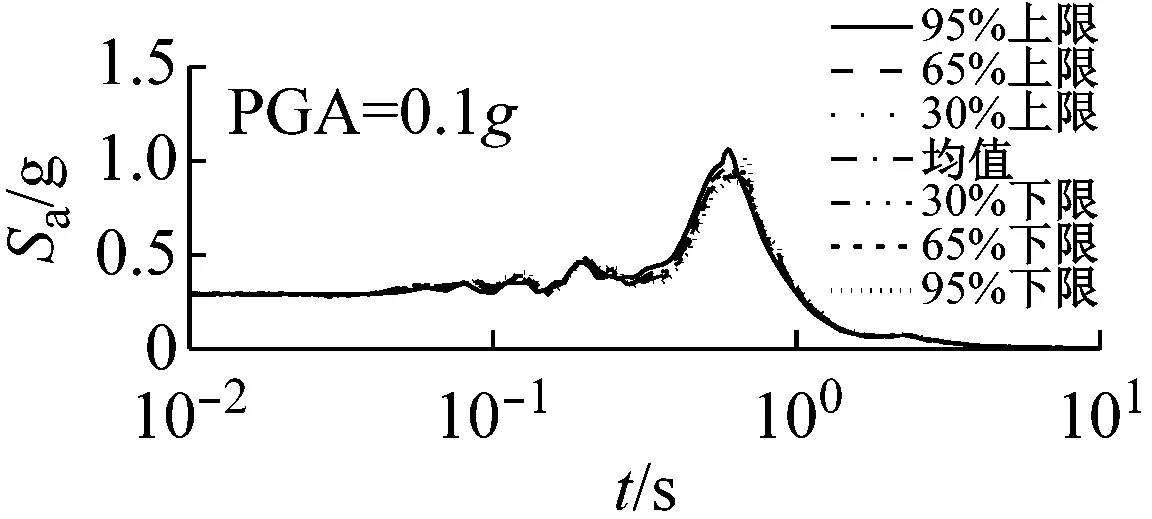
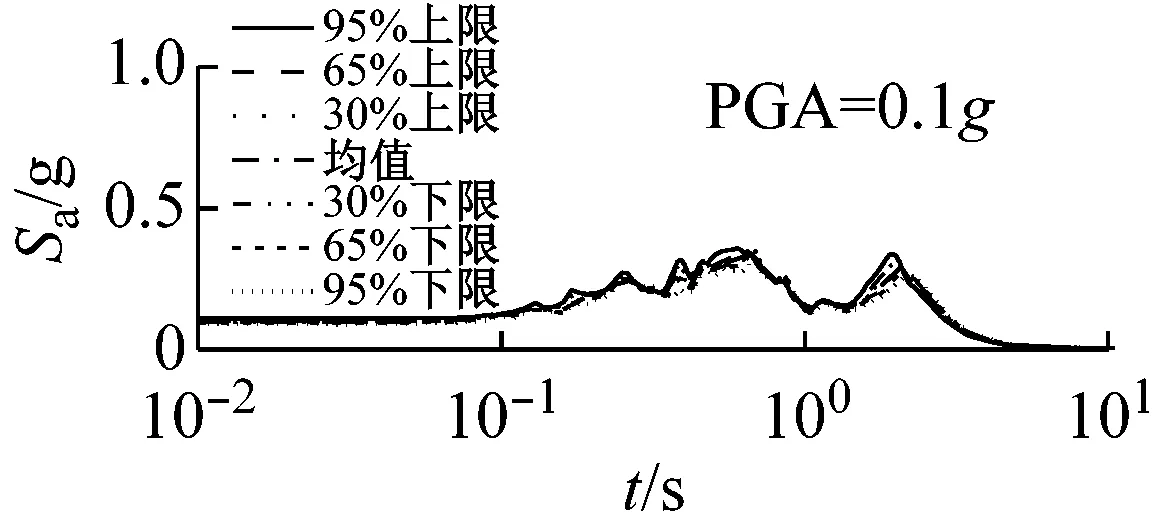
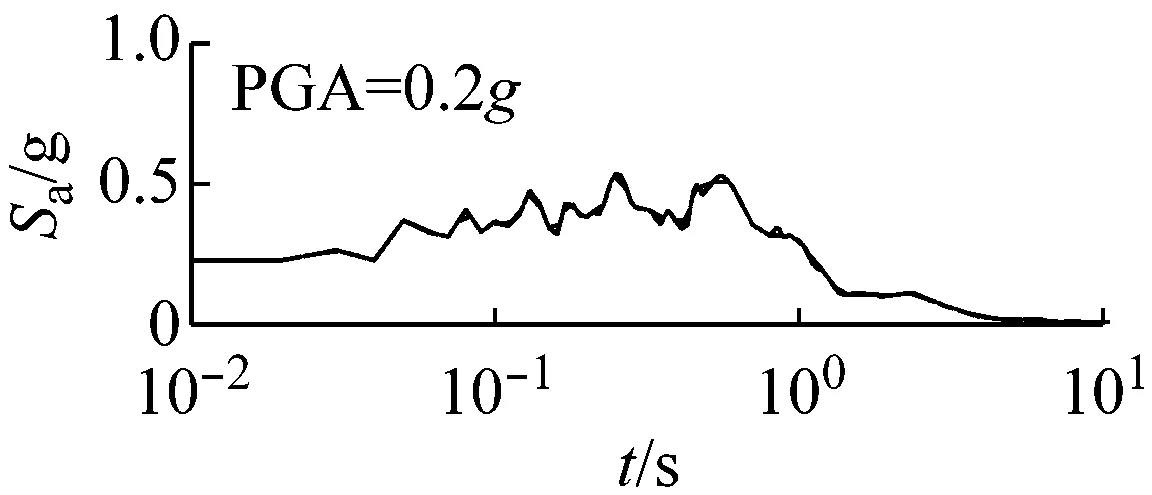
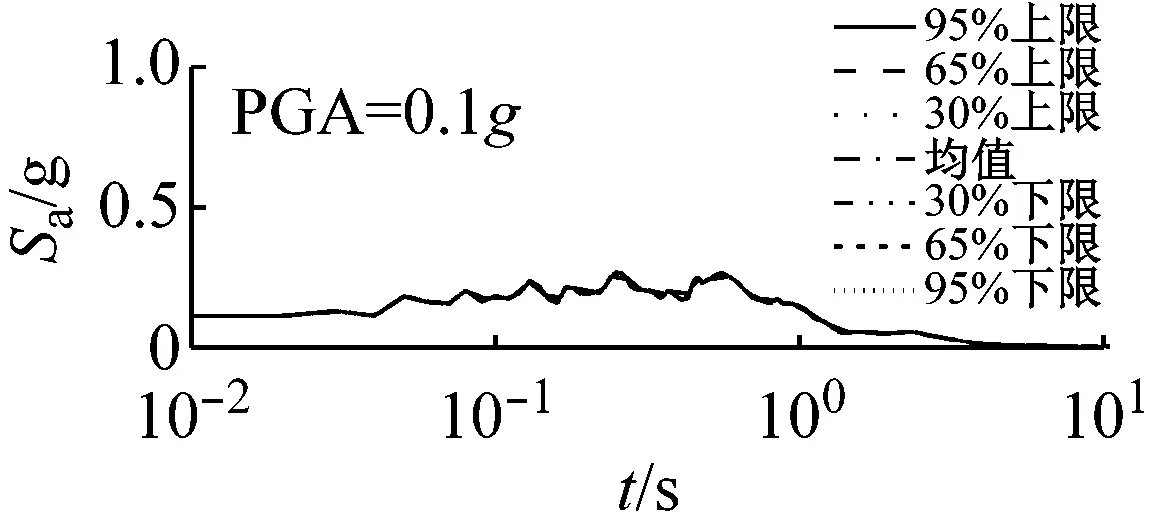
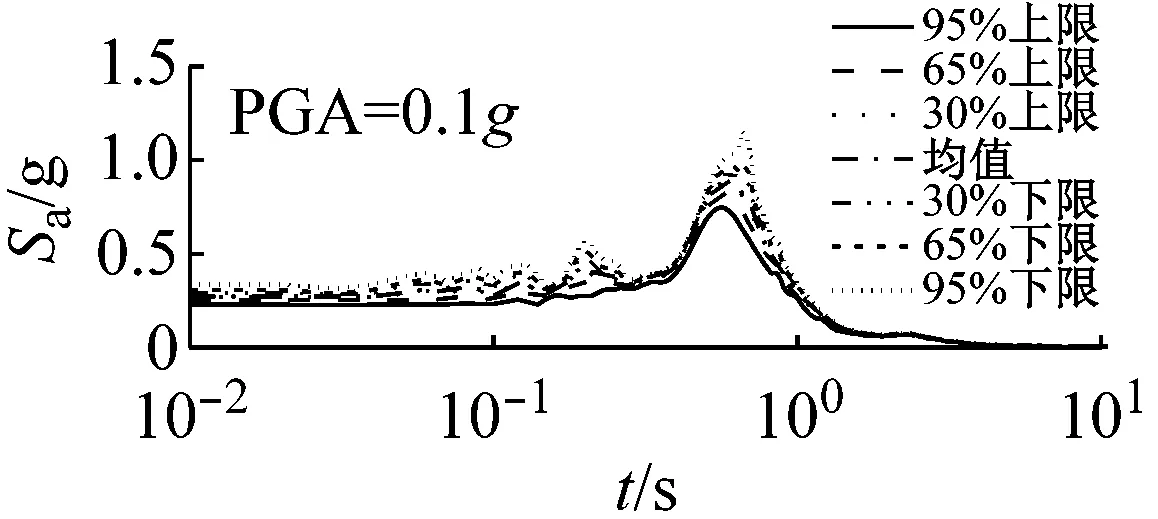
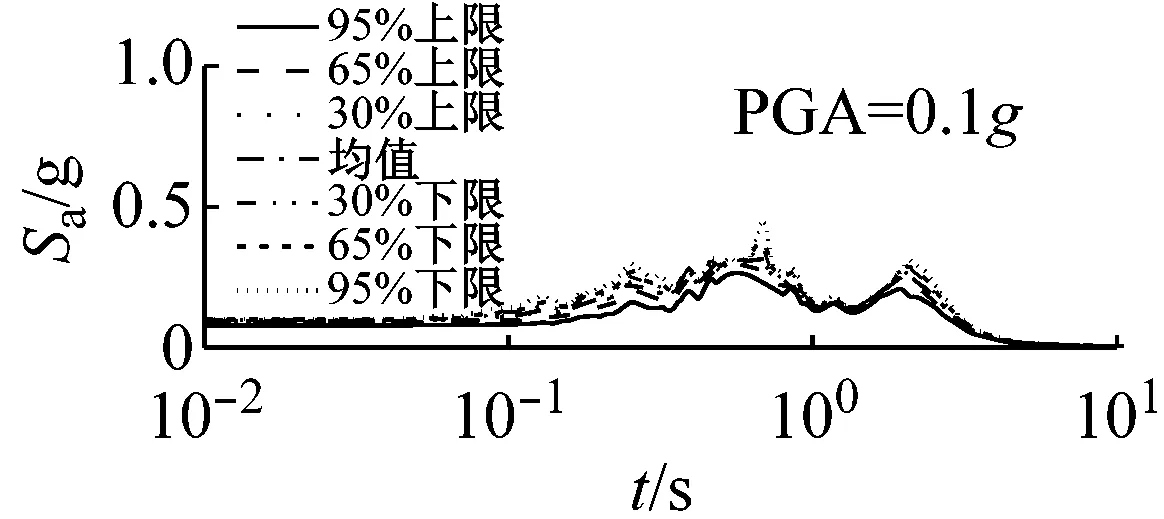
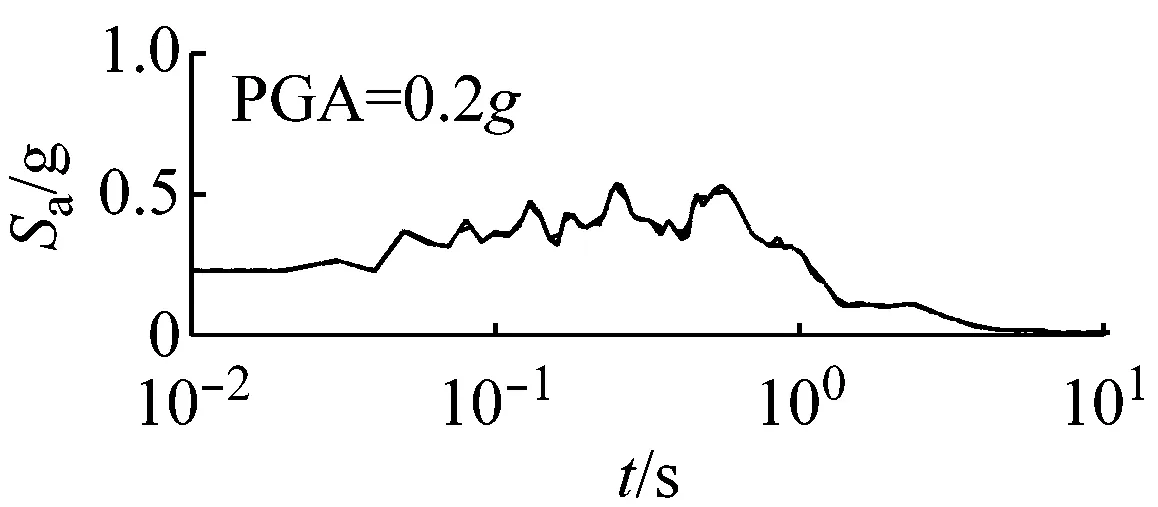
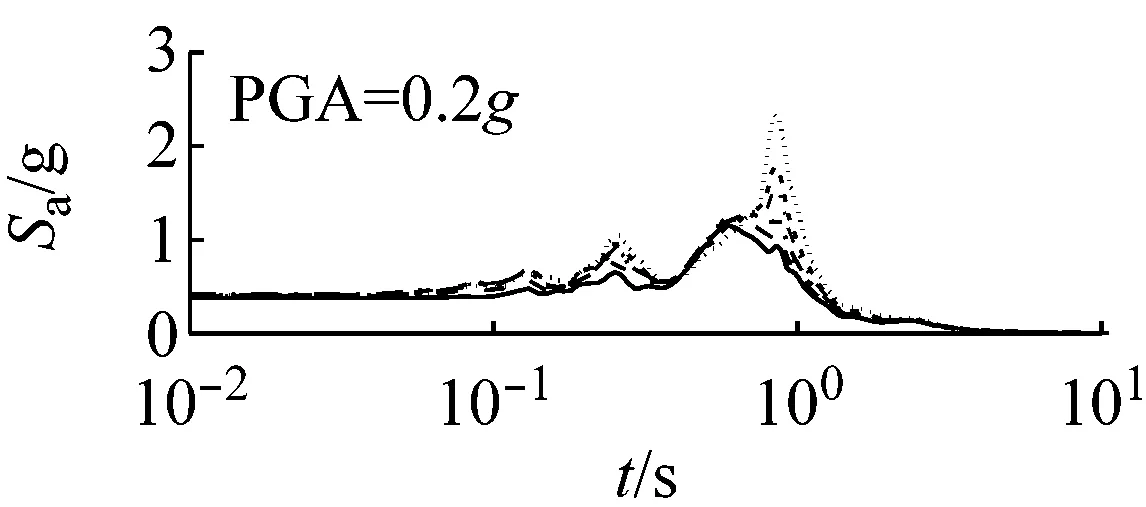
图5和图6以El Centro波输入为例,分别给出了三种类型场地,三种输入加速度峰值下初级组和高级组的动剪切模量比试验误差对加速度反应谱的影响。
由上可知,动剪切模量比试验误差对地震动计算结果有重要影响,影响因素包括试验误差、场地类别、地震强度和地震波形,影响程度随试验误差增大、场地变软和地震强度增加而增大,其中动剪切模量比试验误差和场地类型起主要作用。
由图5可以看出,对于初级组,在硬场地中,输入地震动较小时动剪切模量比的试验误差对反应谱的影响可以忽略;中硬和软场地中,动剪切模量比概率水平在65%范围内时,试验误差对反应谱有较大影响,动剪切模量比概率水平在65%以上,试验误差对反应谱形状影响则更为显著。
由图6可以看出,高级组动剪切模量比试验误差对反应谱的影响较小。在硬和中硬场地中,动剪切模量比的试验误差对反应谱的影响可以忽略;软场地中,动剪切模量比概率水平在95%概率范围内,对反应谱有一定影响,当动剪切模量比概率水平超过95%时,试验误差对反应谱影响较大。
对比图5和图6可以看出,高级组动剪切模量比的试验误差对反应谱的影响远小于初级组的影响。
2.5阻尼比误差影响
2.5.1 阻尼比误差对PGA影响的风险分析
初级组和高级组不同概率水准阻尼比条件下的加速度峰值与非线性取均值时的加速度峰值之间的相对误差见表6。
由表6可知,对于初级组,在硬场地中,加速度峰值的相对误差均在5%以内,阻尼比试验误差对峰值加速度的影响可以忽略;中硬场地中,65%概率范围内阻尼比对峰值加速度的影响可以忽略,超过65%概率范围的阻尼比对峰值加速度的影响不可忽略。软场地中,50%概率范围内阻尼比对峰值加速度的影响可以忽略,超过50%概率范围的阻尼比对峰值加速度的影响不可忽略。
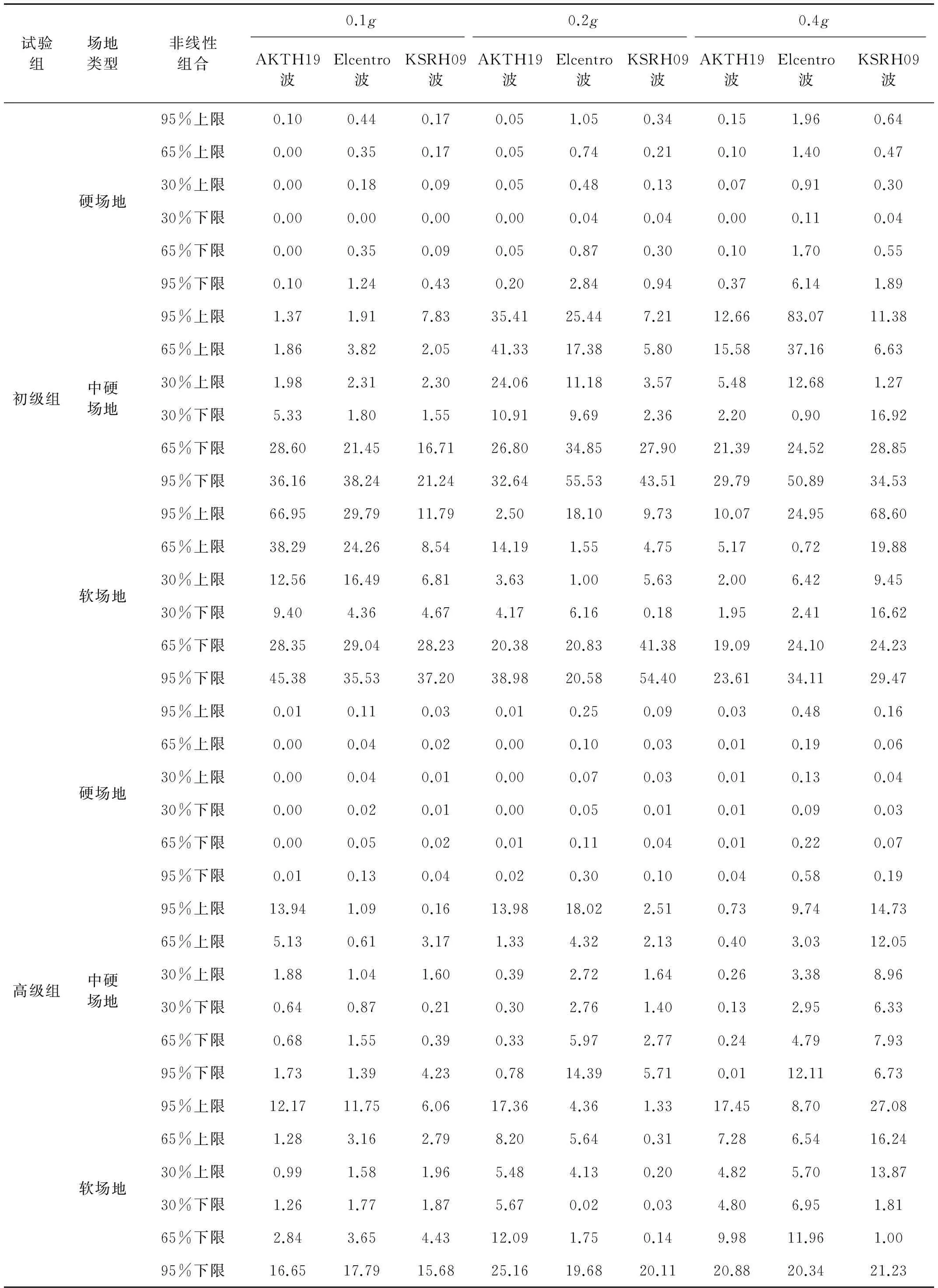
表5 不同概率水准动剪切模量比条件下PGA的相对误差Tab.5 Relative errors of PGA under different probability levels of dynamic shear modulus ratio %

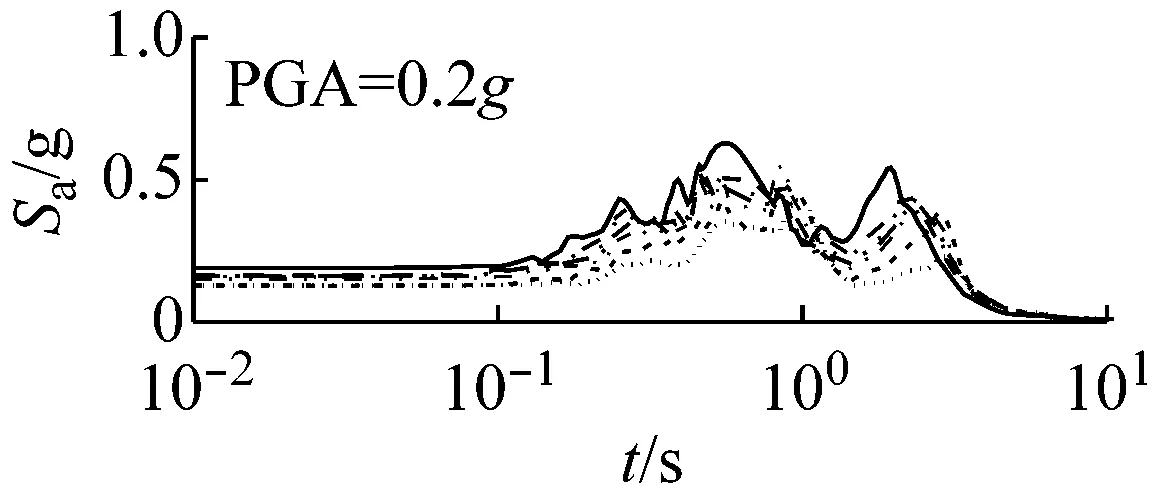
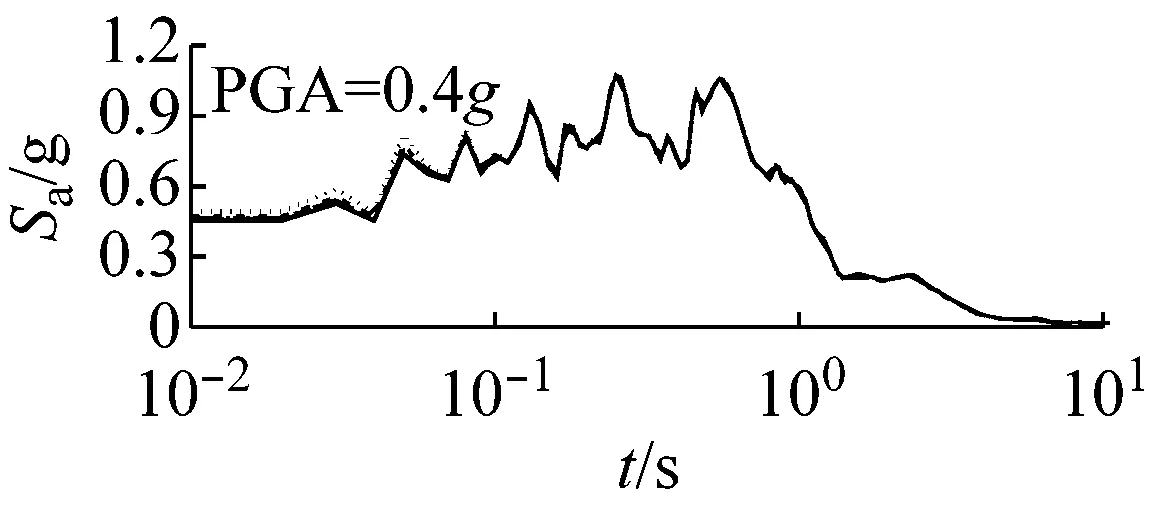
(a) 硬场地
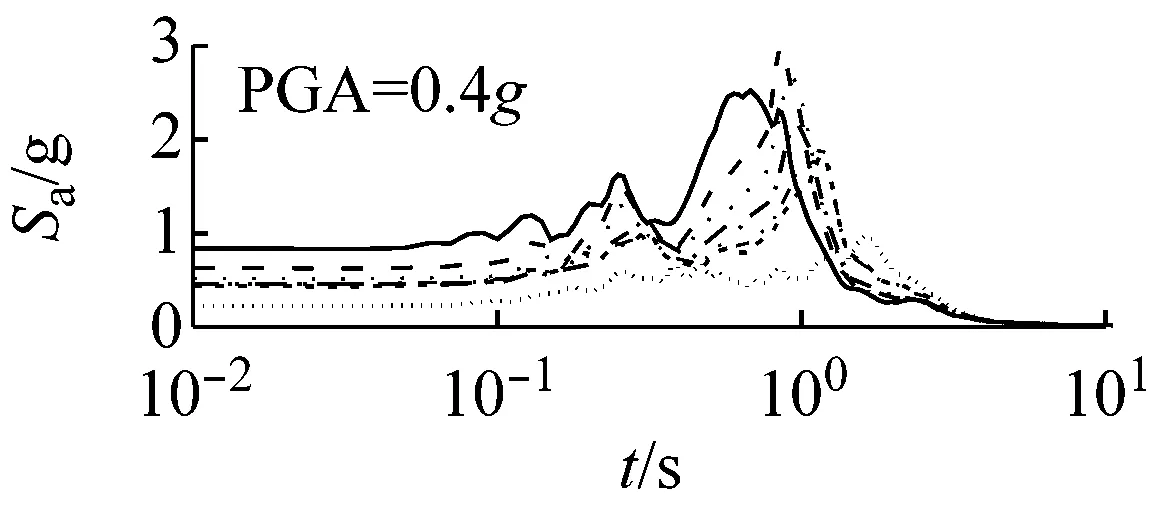
(b) 中硬场地
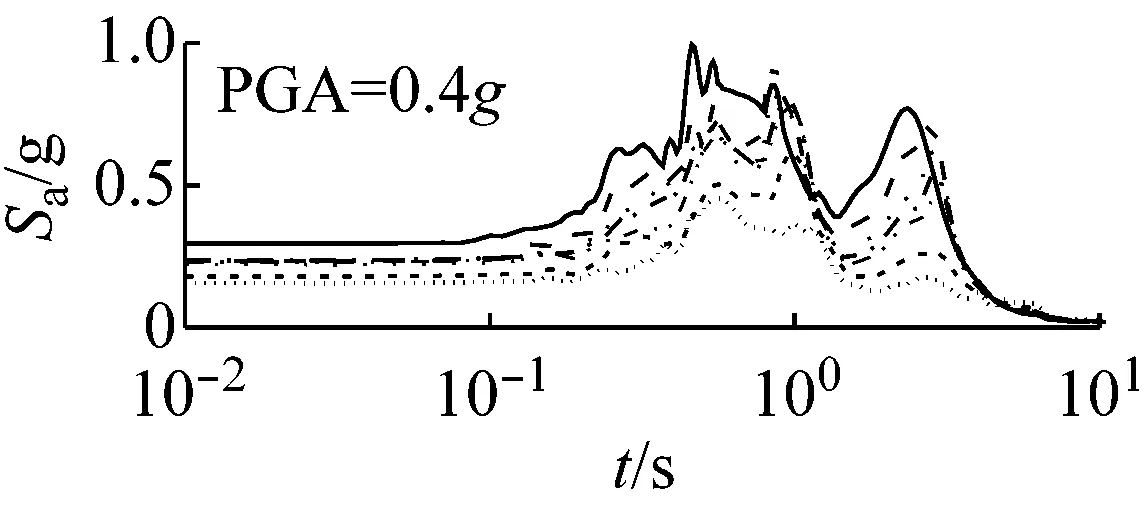
(c) 软场地图5 初级组三种场地、三种强度地震作用下不同概率水平模量比试验误差对反应谱的影响(Elcentro输入)

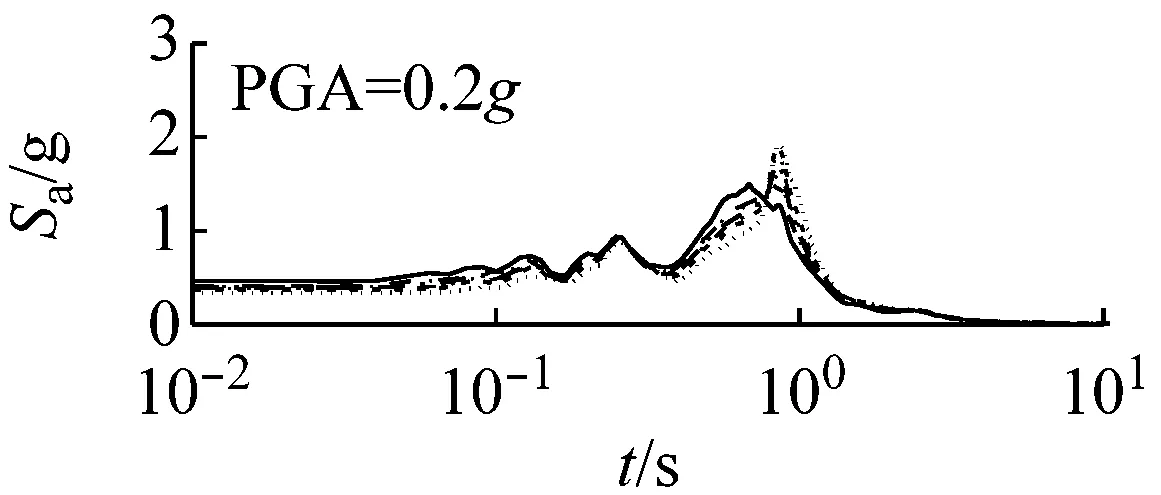
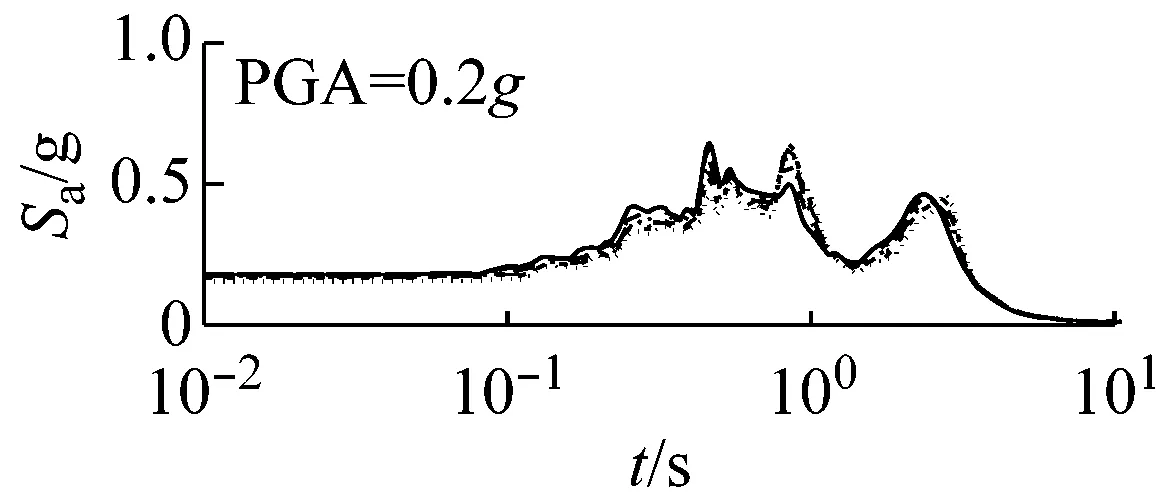
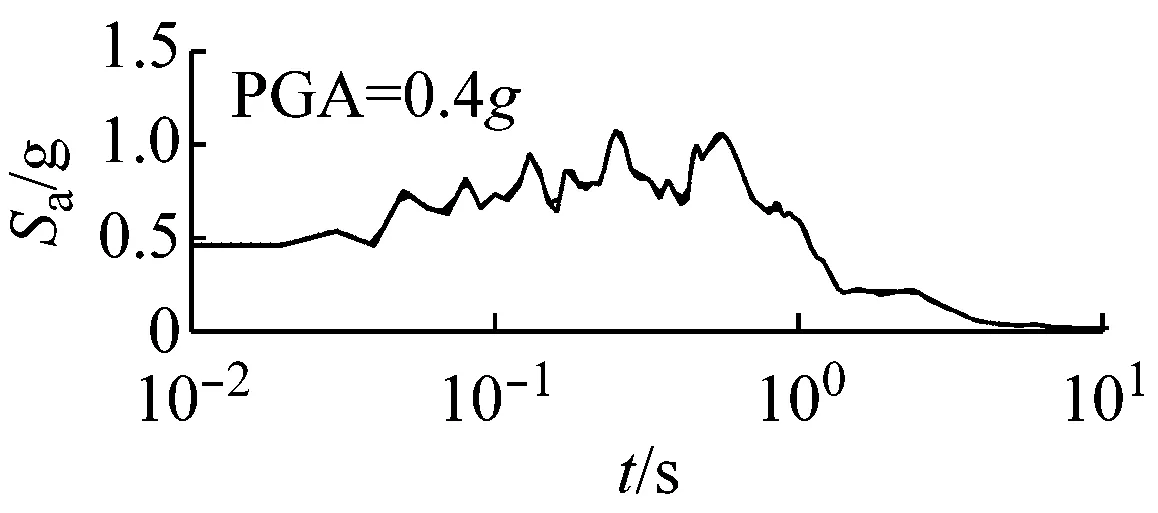
(a) 硬场地
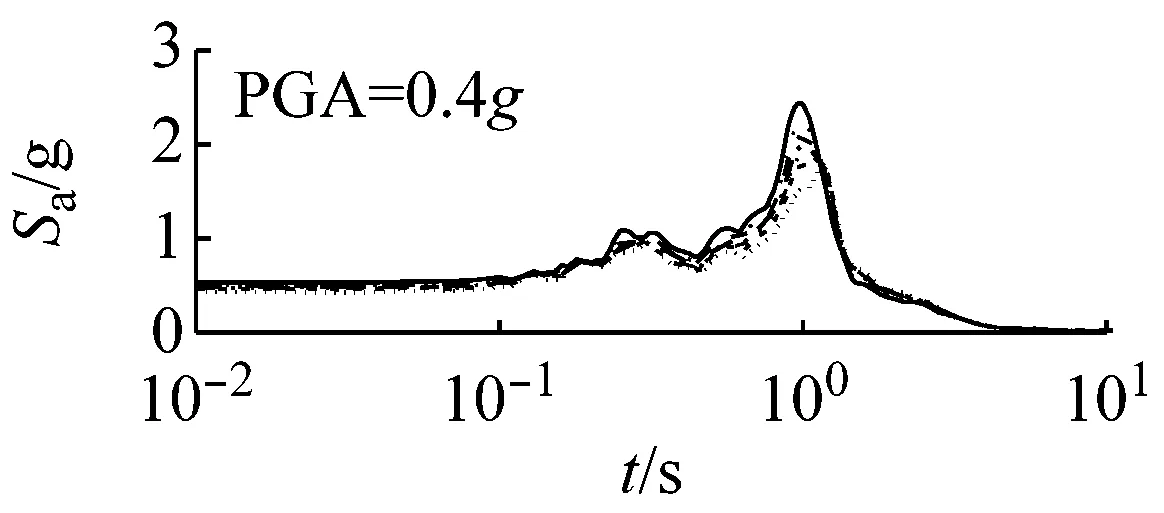
(b) 中硬场地
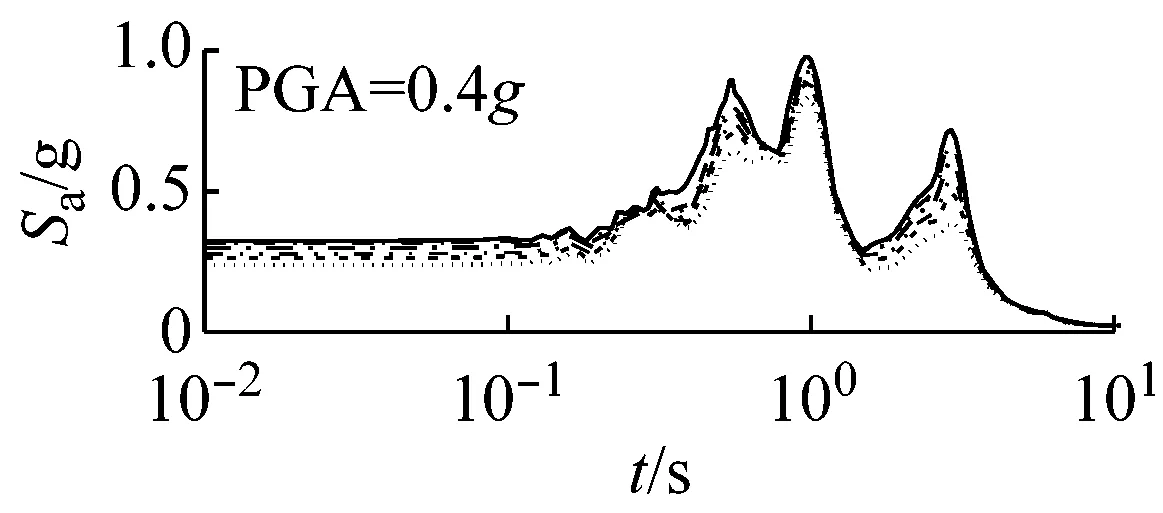
(c) 软场地图6 高级组三种场地、三种强度地震作用下不同概率水平模量比试验误差对反应谱的影响(Elcentro输入)
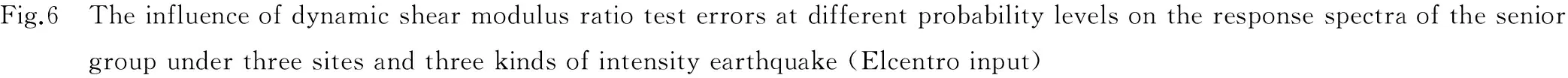
对于高级组,硬、中硬和软场地中,阻尼比试验误差对峰值加速度的影响均可忽略。
综上所述,以对场地地震动产生不可忽视影响为阈值,就初级技术人员的试验,其阻尼比试验误差的风险对硬场地基本可以忽略,对中硬场地的风险水平为35%,对软场地则为50%。技术熟练人员的试验,对硬、中硬、软场地,其阻尼比试验误差的风险水平均接近零。
2.5.2 阻尼比误差对反应谱影响的风险分析
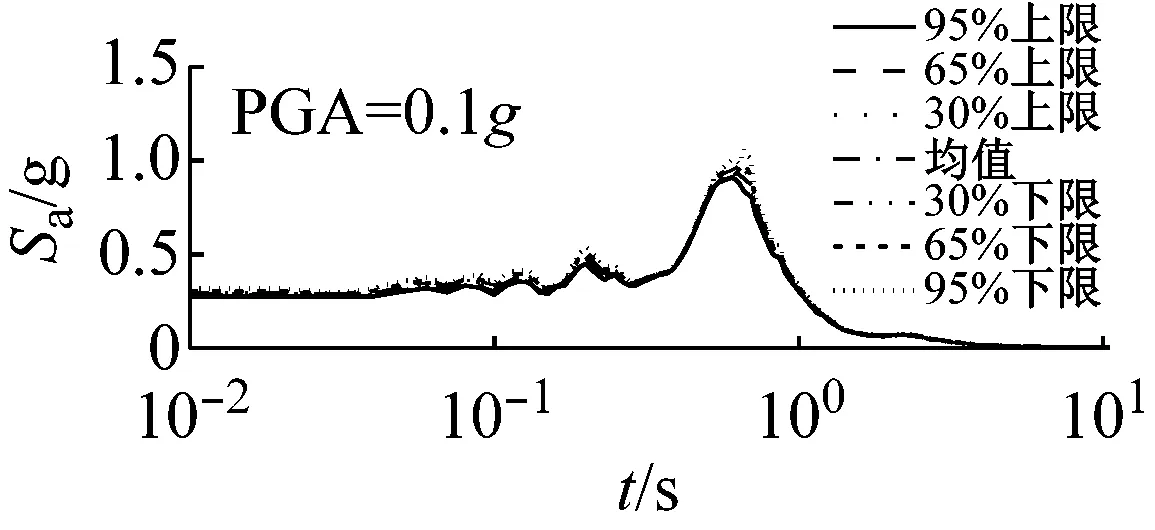
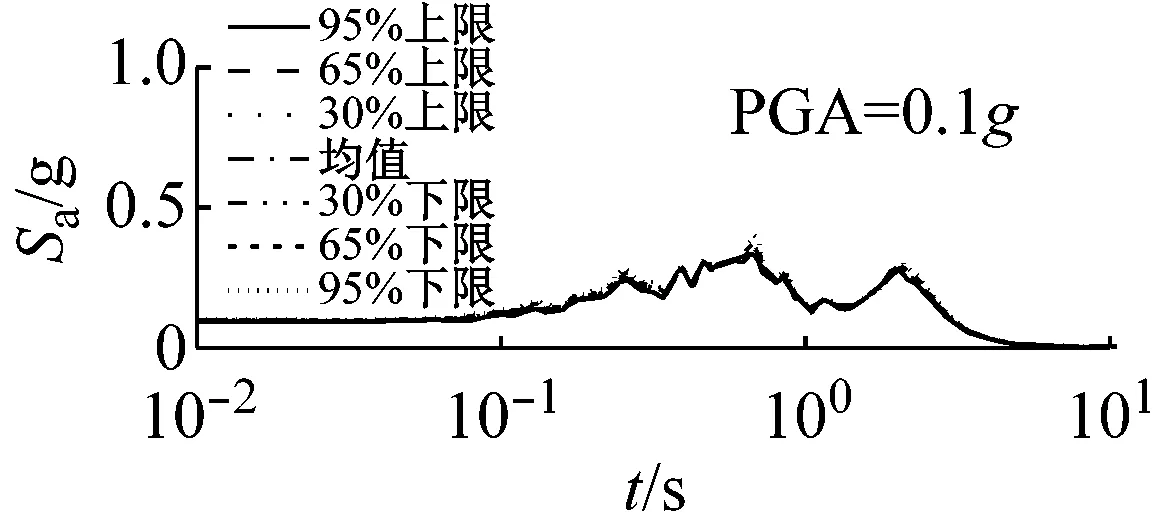
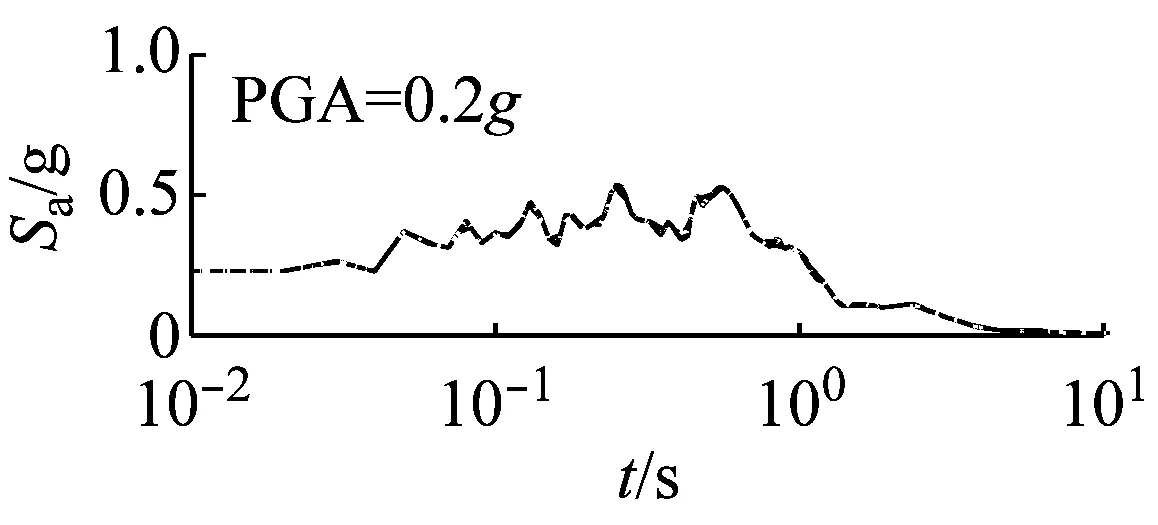
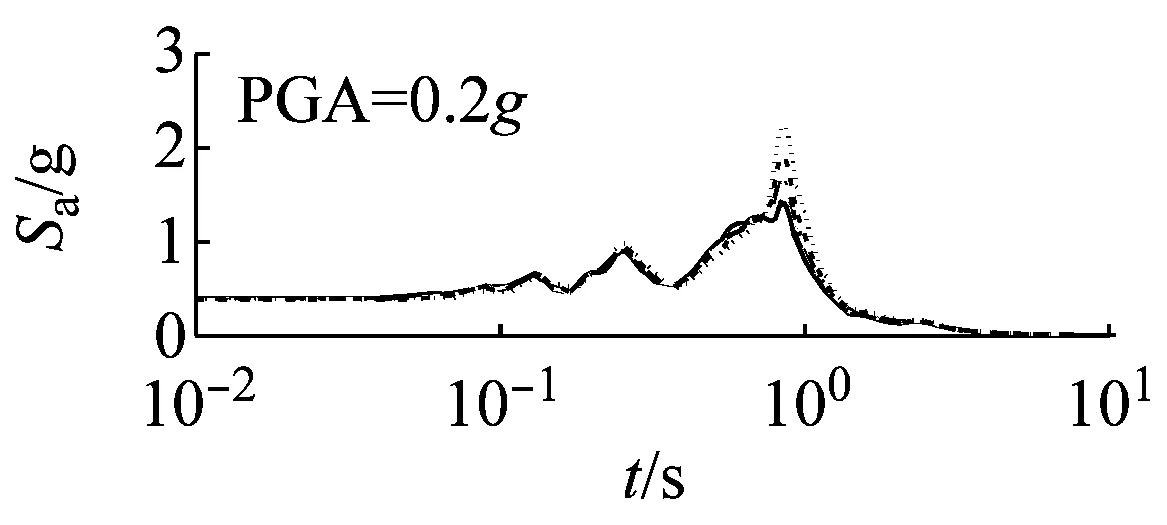
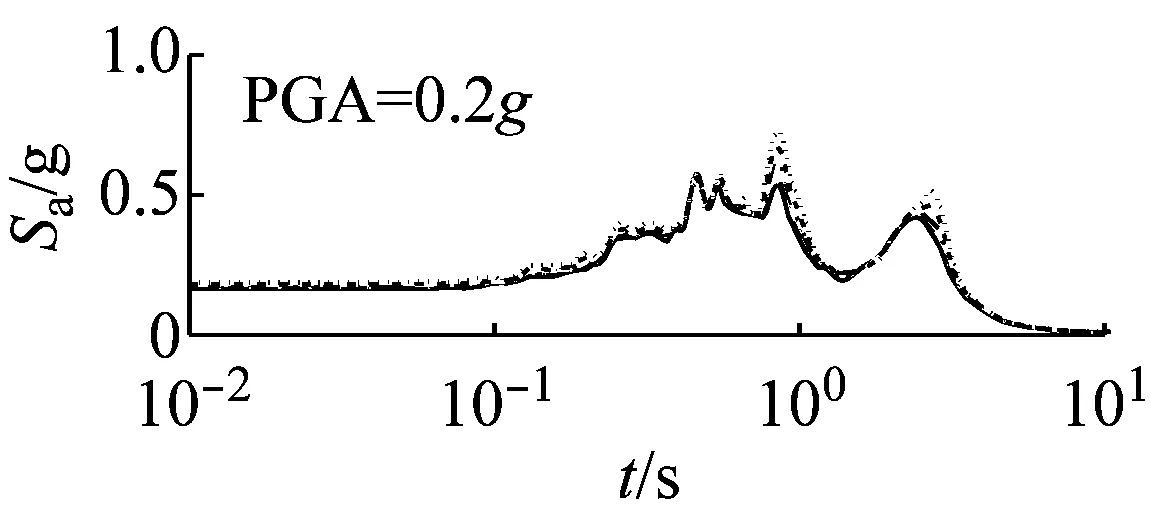
图7和图8以El Centro波输入为例,分别给出了三种类型场地,三种输入加速度峰值下初级组和高级组的阻尼比试验误差对加速度反应谱的影响。
由上可知,阻尼比试验误差对地震动计算结果有重要影响,影响因素包括试验误差、场地类别、地震强度和地震波形,影响程度随试验误差增大、场地变软和地震强度增加而增大,其中阻尼比试验误差和场地类型起主要作用。
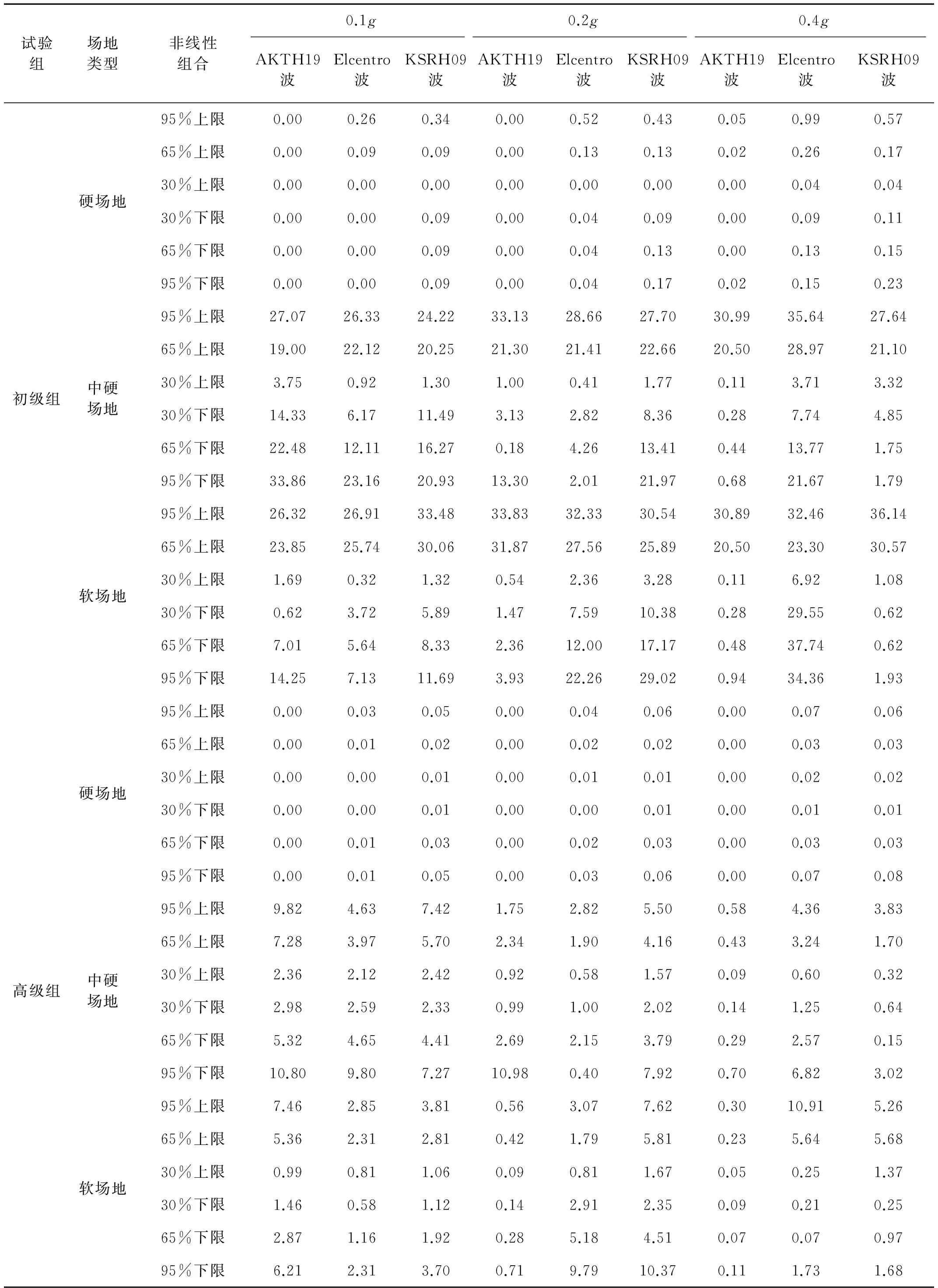
表6 不同概率水准阻尼比条件下PGA的相对误差Tab.6 Relative errors of PGA under different probability levels of damping ratios %
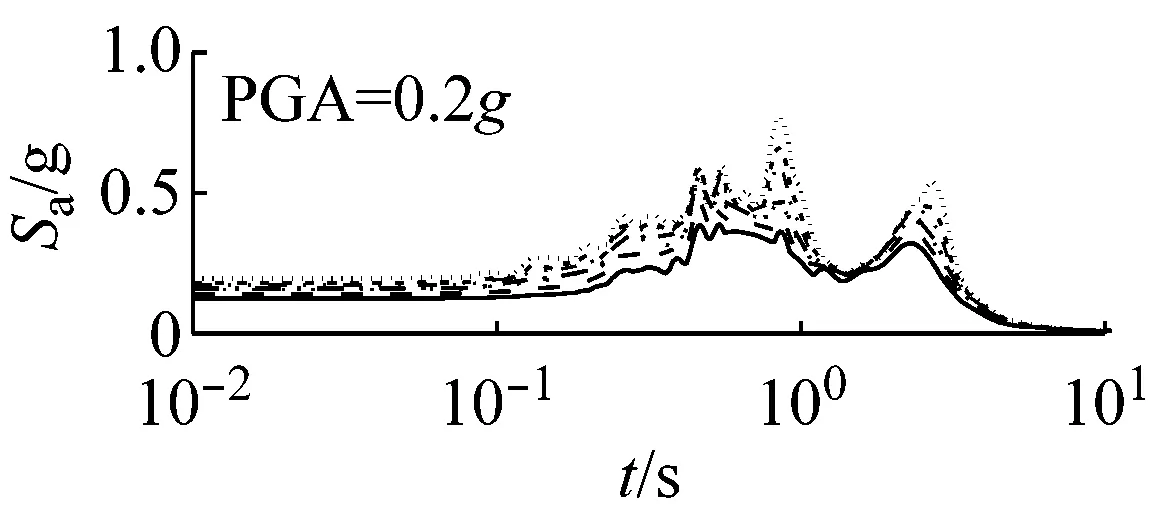

(a) 硬场地
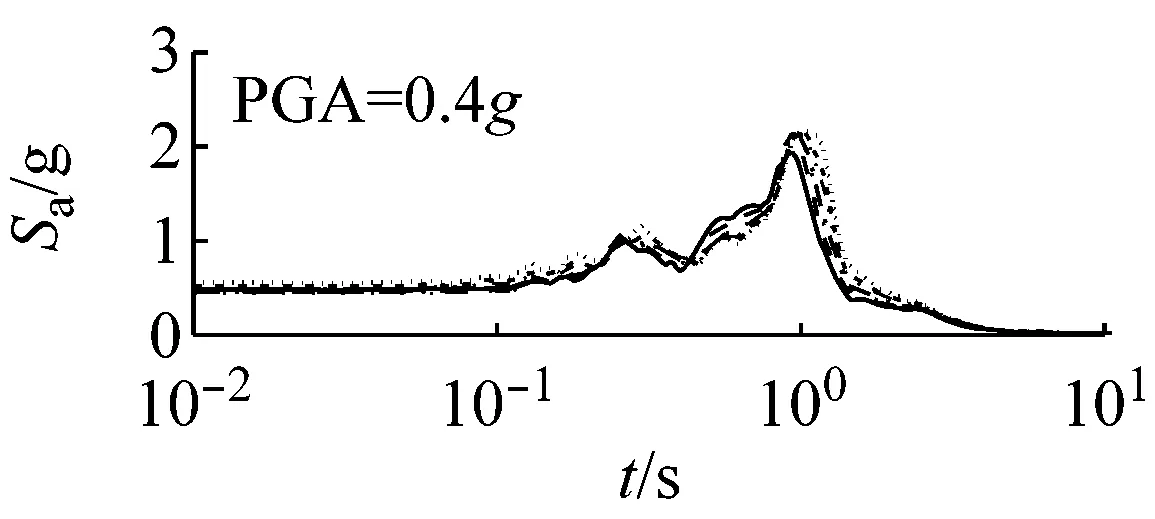
(b) 中硬场地
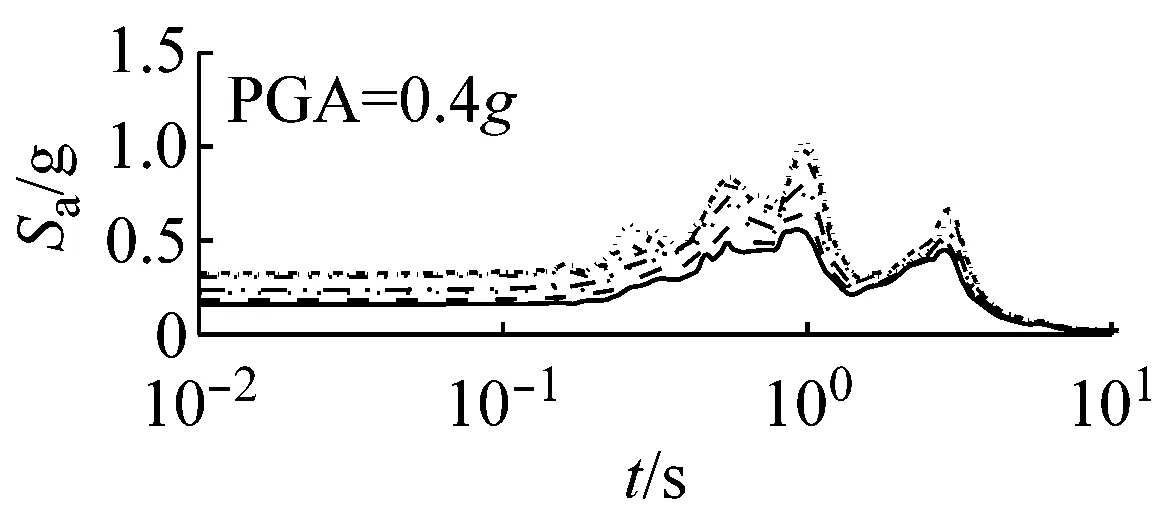
(c) 软场地
图7 初级组三种场地、三种强度地震作用下不同概率水平阻尼比试验误差对反应谱的影响(Elcentro输入)

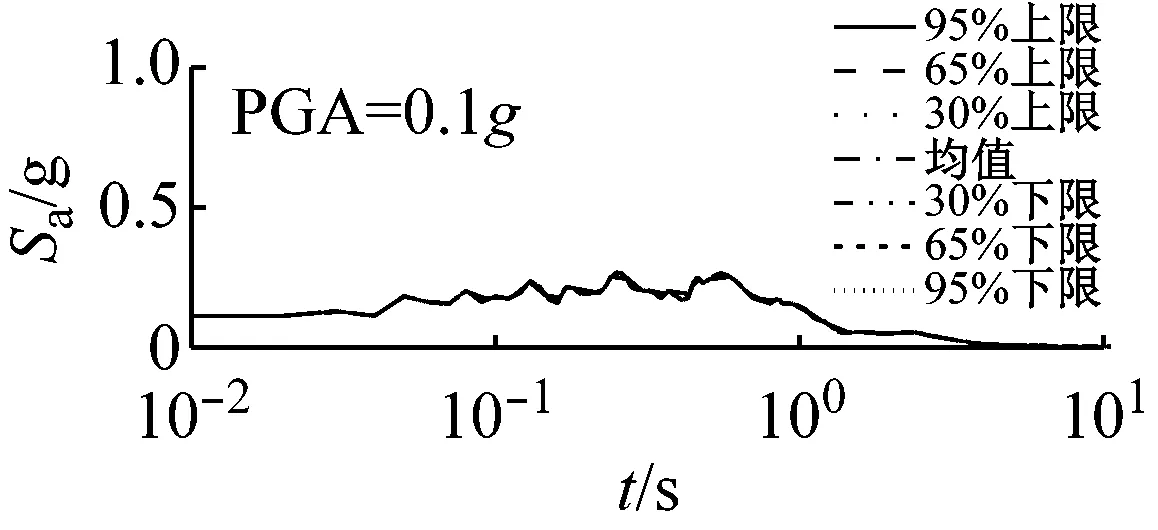
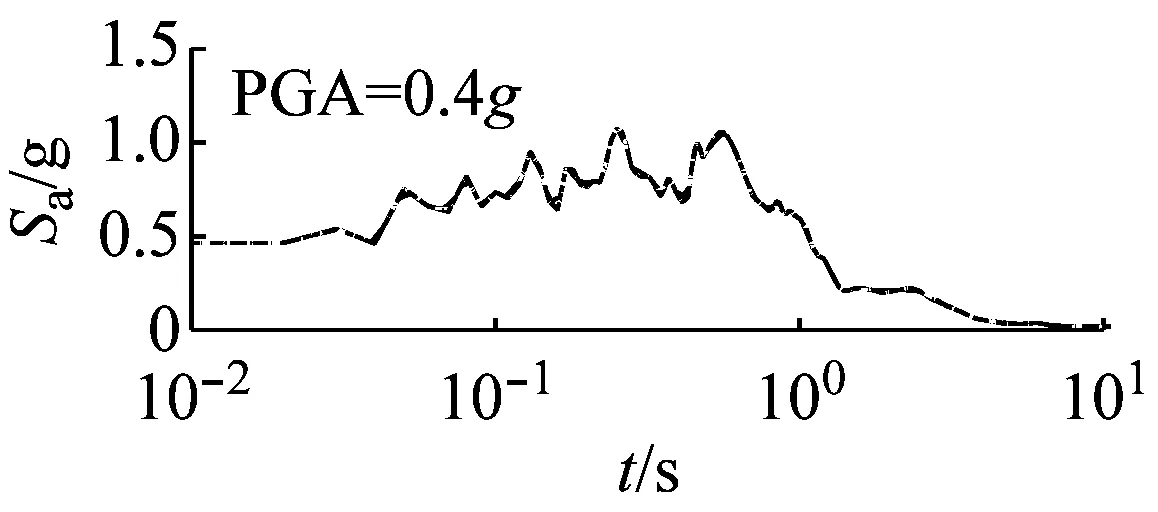
(a) 硬场地
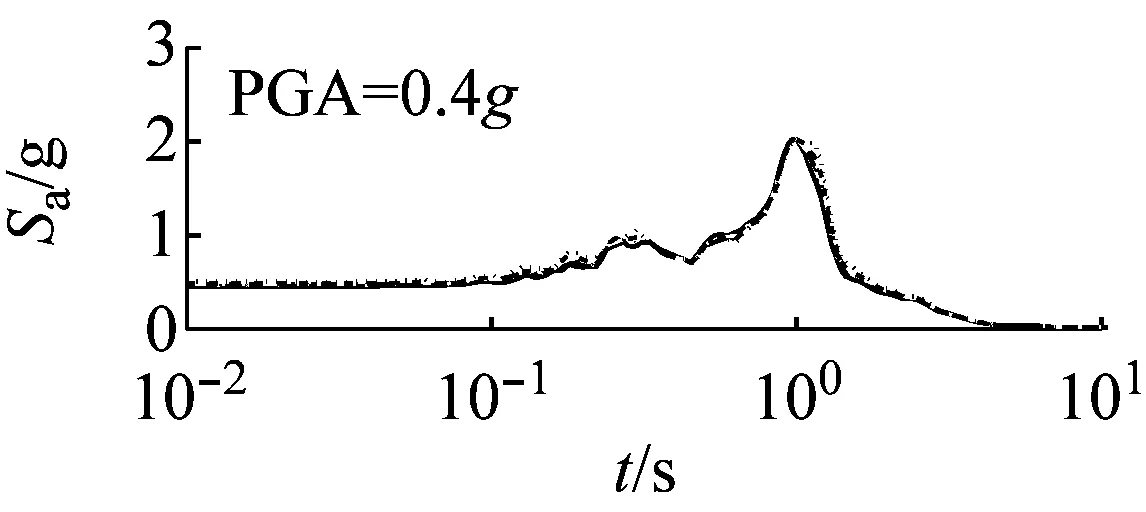
(b) 中硬场地
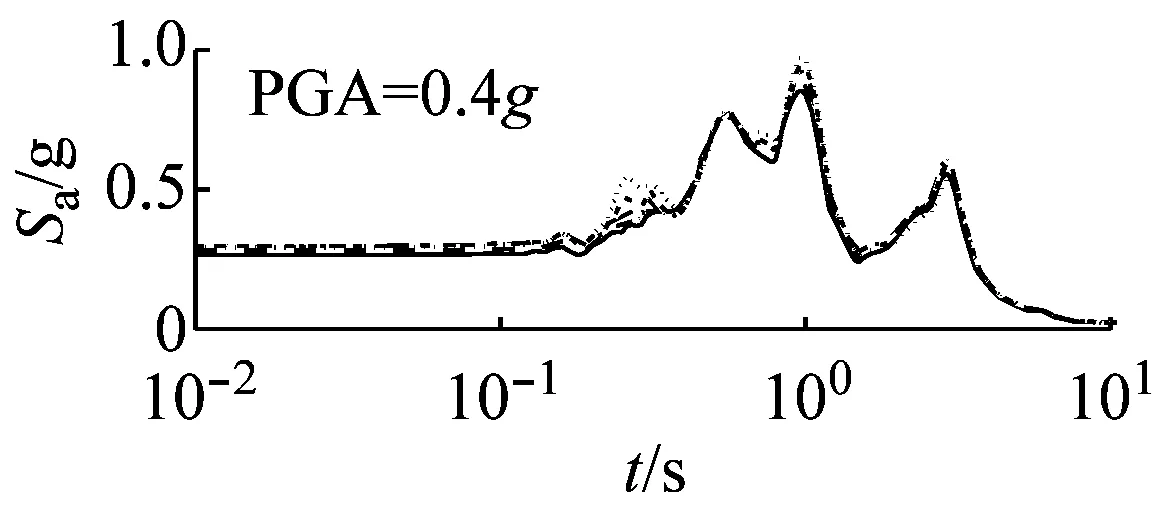
(c) 软场地图8 高级组三种场地、三种强度地震作用下不同概率水平阻尼比试验误差对反应谱的影响(Elcentro输入)

由图7可以看出,对于初级组,硬场地中,阻尼比的试验误差对反应谱的影响可以忽略;中硬、软场地中,阻尼比概率水平在65%以内时,试验误差对反应谱有较大影响,阻尼比概率水平在65%以上,试验误差对反应谱影响则更为显著。
由图8可以看出,硬、中硬和软场地中,高级组阻尼比的试验误差对反应谱的影响均可以忽略。
对比图7和图8可以看出,高级组阻尼比的试验误差对反应谱的影响远小于初级组的影响。
3 结 论
本文从风险分析角度,研究了动剪切模量比和阻尼比试验误差与设计地震动关系,设计了两种典型试验组的动剪切模量比和阻尼比的共振柱试验,得到了试验误差概率分布特征,给出了试验误差对地震动计算结果的影响规律,提出了现有试验条件下动剪切模量比和阻尼比对地震动计算结果影响的风险评价结果。主要结论如下:
(1) 根据统计学原理,得到的共振柱误差试验结果可靠,可用于概率分析。
(2) 两种典型试验组的动剪切模量比和阻尼比试验数据均服从正态分布,二者试验均值接近,但变异系数相差5倍左右,说明试验人员因素及试验技术水平对试验结果可靠性的影响十分显著。
(3) 动剪切模量比和阻尼比试验误差对地震动计算结果有重要影响,影响因素包括试验误差、场地类别、地震强度和地震波形,影响程度随试验误差增大、场地变软和地震强度增加而增大,其中动剪切模量比和阻尼比试验误差及场地类型起主要作用。
(4) 以对地震动产生不可忽视影响为阈值,就技术熟练人员的试验,对硬、中硬场地,其动剪切模量比的试验误差风险水平接近0,对软场地有5%的风险,其阻尼比的试验误差对所有类型场地的风险均接近0。
(5) 以对地震动产生不可忽视影响为阈值,初级技术人员的试验,其动剪切模量比和阻尼比的试验误差风险对硬场地基本可以忽略,对中硬场地的风险水平为35%,对软场地则为50%。
(6) 高水平人员的试验误差对土层地震动评估结果的风险是基本可以忽略的,但就一般情况,应强化共振柱试验技术规程,提高试验人员技术水平,否则会对工程结构的地震动输入估计造成很大风险。
[1] 李小勇, 谢康和, 虞颜. 太原粉质黏土强度指标概率特征[J]. 浙江大学学报(工学版), 2001, 35(5): 492-496.
LI Xiaoyong, XIE Kanghe, YU Yan. Probabilistic characteristics of strength indexes for Taiyuan siltyclay[J]. Journal of Zhejiang University(Engineering Science), 2001, 35(5): 492-496.
[2] 陈龙伟, 汪云龙, 袁晓铭. 土层特性变异性对场地传递函数的影响[J].防灾减灾工程学报, 2014, 31(1): 78-84.
CHEN Longwei, WANG Yunlong, YUAN Xiaoming.Influence of variability of soil characteristics on site transfer function[J].Journal of Disaster Prevention and Mitigation Engineering, 2014, 31(1): 78-84.
[3] 倪万魁, 韩启龙. 黄土土性参数的统计分析[J]. 工程地质学报, 2001, 9(1): 62-67.
NI Wankui, HAN Qilong. Statistical analysis of physical and mechanical indexes of the typical loess[J]. Journal of Engineering Geology, 2001, 9(1): 62-67.
[4] 王绍博, 丁海平. 土动力学参数对土层动力反应的影响[J]. 地震工程与工程振动, 2001, 21(1): 105-108.
WANG Shaobo, DING Haiping. Effect of soil dynamic parameters on seismic response of soil layers[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(1): 105-108.
[5] 工程场地地震安全性评价技术规范:GB 17741—2005[S].北京: 中国标准出版社, 2005.
[6] 祝龙根, 杜坚. 不同类型共振柱仪对比实验[J]. 水电自动化与大坝监测, 1990(3): 26-32.
ZHU Longgen, DU Jian. Comparison tests with different types of resonant column devices[J]. Hydropower Automation and Dam Monitoring, 1990(3): 26-32.
[7] 袁晓铭, 孙锐, 孙静, 等. 常规土类动剪切模量比和阻尼比试验研究[J]. 地震工程与工程振动, 2000, 20(4): 133-140.
YUAN Xiaoming, SUN Rui, SUN Jing, et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils[J].Earthquake Engineering and Engineering Vibration, 2000, 20(4): 133-140.
[8] 孙静, 袁晓铭. 土的动模量和阻尼比研究述评[J].世界地震工程, 2003, 19(1): 88-95.
SUN Jing, YUAN Xiaoming. A state-of-art of research on dynamic modulus and damping ratio of soils[J].World Earthquake Engineering, 2003, 19(1): 88-95.
[9] 陈国兴, 刘雪珠, 王炳辉. 土动力参数变异性对深软场地地表地震动参数的影响[J]. 防灾减灾工程学报, 2007, 27(1): 1-10.
CHEN Guoxing, LIU Xuezhu, WANG Binghui. Effect of variability of soil dynamic parameters on ground motion parameters for deep soft sites[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(1): 1-10.
[10] 兰青龙, 贺明华, 安卫平. 太原地区场地土动力性能的统计分析[J]. 山西地震, 1997(3): 6-11.
LAN Qinglong, HE Minghua, AN Weiping. Several features of earthquake swarm in Taiyuan basin[J]. Earthquake Research in Shanxi, 1997(3): 6-11.
[11] 李剑, 陈善雄, 姜领发, 等. 重塑红黏土动剪切模量与阻尼比的共振柱试验[J]. 四川大学学报(工程科学版), 2003, 45(4):62-68.
LI Jian, CHEN Shanxiong, JIANG Lingfa, et al. Resonant column teston dynamic shear modulus and damping ratio of the remolded red clay[J].Journalof Si Chuan University(Engineering Science), 2003, 45(4):62-68.
[12] IDRISS I M, SEED H B. Seismic response of horizontal soil layers[J].Journal of the Soil Mechanics and Foundations Division, 1968, 94(4):1003-1031.
[13] 孙锐, 袁晓铭, 刘晓健. 动剪切模量比与剪切波速对地震动影响及等量关系研究[J]. 岩土工程学报, 2009, 31(8): 1267-1274.
SUN Rui, YUAN Xiaoming,LIU Xiaojian.Effects of dynamic shear modulus ratio and velocity on surface ground motion and their equivalent relations[J].Chinese Journal of Geotechnical Engineering, 2009, 31(8): 1267-1274.
[14] 陈红娟. 土动力非线性的变异性及其对地震动影响的概率分析[D]. 哈尔滨: 中国地震局工程力学研究所, 2009.
[15] 李晓飞, 孙锐, 袁晓铭, 等. 现有等效线性化分析程序在实际软场地计算结果方面的比较[J]. 自然灾害学报, 2015, 24(4): 56-62.
LI Xiaofei, SUN Rui, YUAN Xiaoming, et al. Comparison of existing equivalent linear response analysis program for actual soft site in KiK-net array[J].Journal of Natural Disaster, 2015, 24(4): 56-62.
[16] 土工实验规程:SL 237—1999[S]. 北京:中华水利水电出版社, 1999.
[17] MENDENHALL W,SINCICH T,门登霍尔,等. 统计学[M]. 北京: 机械工业出版社, 2014.
Testerrorsofdynamicshearmodulusanddampingratioandtheireffectsontheriskassessmentforsurfacegroundmotions
LI Xiaofei1,2,WANG Yunlong1,SUN Rui1,LI Bo2
(1. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China; 2. School of Architecture Engineering, Binzhou University, Binzhou 256600, China)
To study the effects of testing errors on the risk assessment for ground motions, the testing errors of dynamic shear modulus and damping ratio by using the resonant column apparatus and their probability distribution characteristics were investigated. The influences of testing errors on the calculation of surface ground motions were analyzed and the risk level of the influences was studied by numerical simulations. Two experimental groups representing the largest and the smallest dispersion were designed, and then the probability distribution characteristics of the testing errors were provided. A numerical simulation was carried out, in which the risk assessment for surface ground motions was implemented by inputting typical seismic motions with varying amplitudes on three classes of sites. The results show that the testing errors of dynamic shear modulus ratio and damping ratio of the two groups are both normally distributed with close mean values, but the variation coefficients of the two groups are differed by 5 times. The influences of testing errors on surface ground motions increase with the increase of testing errors, softening of site and earthquake intensity, among them the testing errors and site classes play the major roles. Taking whether the influences on surface ground motions can be ignored or not as a threshold, due to the testing errors made by preliminary technicians, the risk assessment for medium stiff site is 35% and that for soft site is 50%. Therefore, it is suggested to strengthen the technical regulations of resonance column tests, and to improve the technicians’ skill, otherwise it will cause significant risk to engineering structures under ground-motions.
dynamic shear modulus ratio and damping ratio; test error; probability distribution; ground motion; risk assessment
TU411
A
10.13465/j.cnki.jvs.2017.19.030
国家科技支撑计划项目(2015BAK17B01); 国家重点研发计划政府间国际科技创新合作重点专项(2016YFE0105500);中央级公益性研究所基本科研业务费专项(2016A02);滨州学院科研启动基金项目(2016Y26)
2016-01-18 修改稿收到日期:2016-08-03
李晓飞 女,博士,1988年8月生
汪云龙 男,博士,助理研究员,1985年4月生
