Kagome夹心板的多模态压电分流振动控制研究

郭空明，徐亚兰

(西安电子科技大学 机电工程学院 应用力学研究中心，西安 710071)

Kagome夹心板的多模态压电分流振动控制研究

郭空明，徐亚兰

(西安电子科技大学 机电工程学院 应用力学研究中心，西安 710071)

针对Kagome夹心板的多模态振动控制问题，提出了一种独立模态压电分流振动控制方法。建立了结构与压电换能器耦合系统的有限元模型，之后详细阐述了Kagome夹心板的独立模态压电分流振动控制策略，并针对自由振动问题提出了一种实用的多分流电路参数优化方法。结果表明，提出的控制方法能显著提高Kagome夹心板结构的阻尼特性，加快自由振动的衰减，同时各压电分流电路之间具有很好的独立性。

Kagome 夹心板；多模态振动控制；压电分流振动控制；自由振动

在工程应用中，新材料的作用日渐突出。Kagome夹心板[1]作为超轻多孔材料的一种，除了具有此类材料的各种优越性能外，在振动控制方面较之传统板结构也有明显的优势。Kagome夹心板的一个板面被Kagome类型的平面刚架所代替，该结构的特点是面板的面外变形与平面刚架的面内变形具有很强的耦合，若将平面刚架的杆件替换为作动器，作动器施加的面内力可以实现面板的面外变形。因此通过将少部分平面刚架的杆件替换为阻尼器或作动器，可分别实现其被动[2]和主动振动控制[3]，从而避免了在面板表面黏贴约束层阻尼或压电片，也就不会影响面板的形状。

对于板壳等结构，振动是无法回避的一个问题。传统的振动抑制方法大致可以分为动力吸振[4]、阻尼材料耗能减振(被动控制)[5]、主动控制[6]以及半主动控制[7]等。其中，动力吸振需要给原结构附加显著的质量，也会占用一定的空间。传统被动耗能控制的效果受制于阻尼材料的特性，可优化的余地不多。主动控制虽然较为灵活，设计余地大，但需要测量、反馈环节，因此存在可靠性问题。半主动控制是在被动耗能控制中引入主动改变参数的环节的一种控制方法，目前此类控制技术如磁流变、电流变等也需要给结构附加相当的质量，因此应用领域具有局限性。

压电分流阻尼振动控制是一种将机械能转化为电能再进行耗散的方法。压电分流电路可以分为谐振分流电路[8]、负电容分流电路[9]，以及半主动范畴的状态开关分流电路[10]等，其中谐振分流电路运用较广。其原理和吸振器类似，虽然理论上需要的电感线圈质量也很大，但可以用多种等效电路方法去合成电感，从而避免了大质量的问题。而与传统使用阻尼材料的耗能减振方法相比，谐振电路又具有良好的可设计性。谐振分流电路的缺点是电路的通频带很窄，因此对结构的固有频率非常敏感。

为了使用谐振分流电路控制振动中的多阶模态分量，传统的方法需要使用复杂的隔流电路[11]、电路网络[12]等，由于电路中元件众多，只要其中一个元件失效，所有阶模态的控制效果都将受到严重影响。而且一旦结构的固有频率发生改变，重新调谐会非常复杂。针对这个问题，本文提出了一种独立模态压电分路阻尼的方法，该方法最大的特点在于每阶模态由一条分路独立控制，各分路之间独立性强，因此控制可靠性好，即使其中一个分路出现问题，也不会对其它模态的控制效果产生显著影响。而且与隔流电路等方法相比，使用的电子元件要少得多。

本文针对Kagome夹心板使用独立模态压电分路阻尼进行振动控制，并针对自由振动问题提出了一种实用可行的谐振电路参数优化方案。通过仿真结果验证了该方法的有效性。

1 Kagome夹心板及压电换能器的有限元模型

1.1悬臂Kagome夹心板的有限元模型

Kagome夹心板(见图1)由面板(深灰色)，四面体状的夹心层(灰色)和Kagome平面刚架(黑色)构成。组成刚架的杆件在形状、尺寸及材料上完全相同。

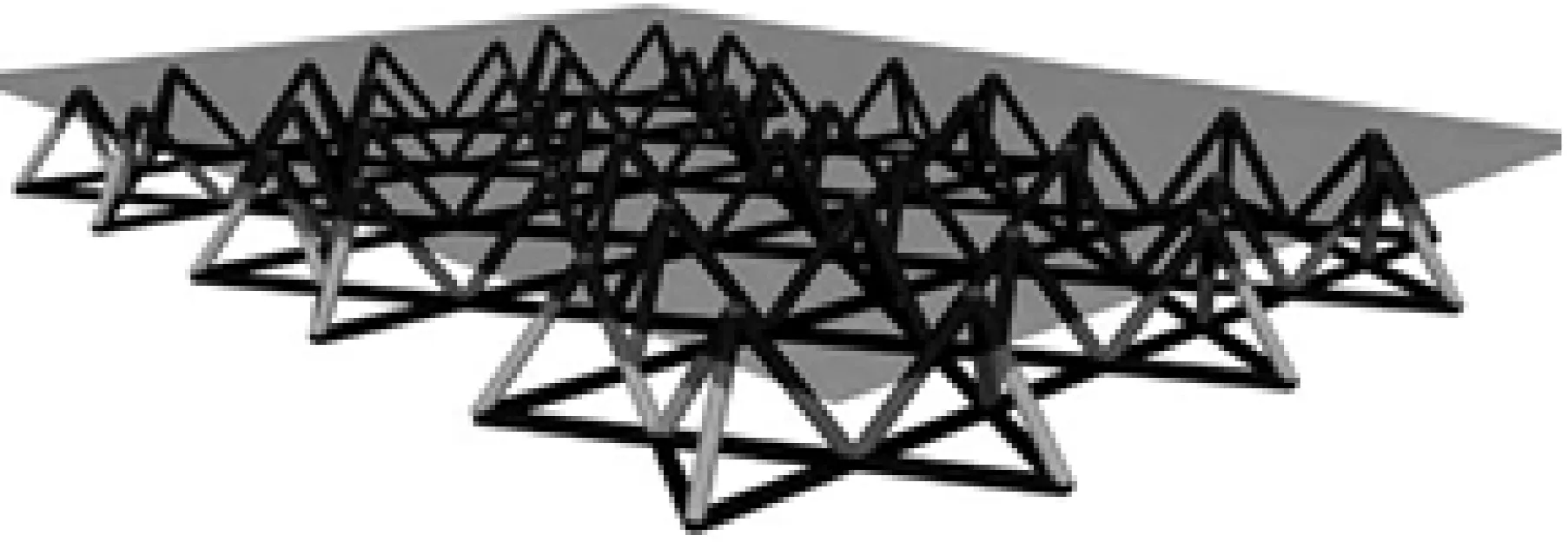
图1 Kagome夹心板示意图Fig.1 Schematic of Kagome sandwich plate

本文研究的Kagome夹心板结构的有限元模型及面板的划分网格如图2所示。每根杆件作为一个梁单元。边界条件为四边固支。面板和杆件的参数见表1。计算出的前六阶模态的固有频率分别为297 Hz，507 Hz，550 Hz，717 Hz，775 Hz和836 Hz。

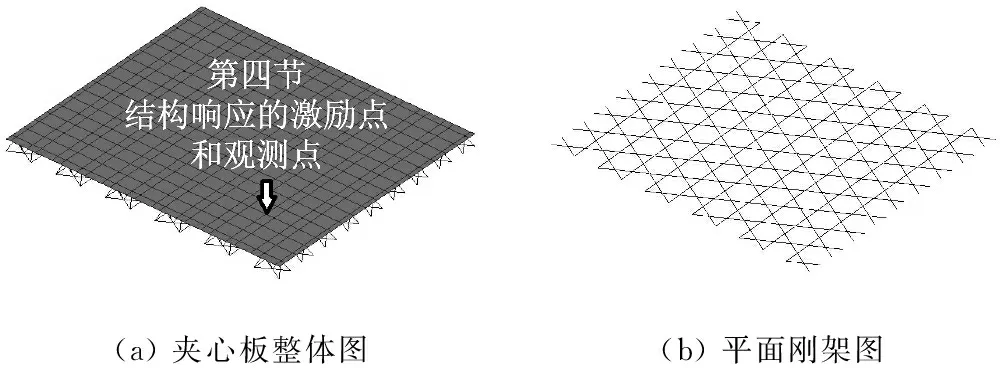
(a)夹心板整体图(b)平面刚架图

1.2机电耦合系统的有限元模型

为了实施压电分流振动控制，需要将平面刚架的少量杆件替换为压电换能器。压电换能器由压电堆，球铰，预压弹簧、外套等部件构成，其结构如图3所示，其中球铰可以防止压电堆受到弯曲作用。各尺寸分别为：rp=3 mm，Lp=31 mm，L1=L2=7 mm，r1=r2=2 mm。

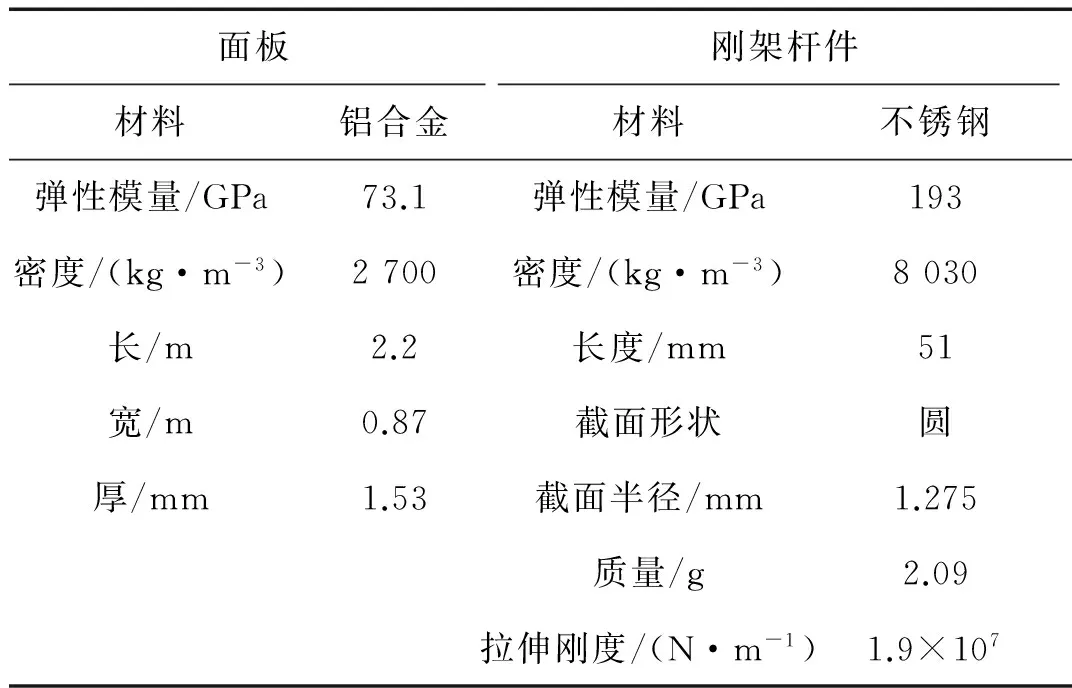
表1 面板和刚架杆件的材料及尺寸Tab.1 Material parameters and size of face sheet and frame rods

在设计的尺寸下，两连杆的刚度远大于压电堆刚度，因此可以认为压电换能器的刚度近似等于压电堆刚度，其短路刚度为Ka=1.5×107N/m。忽略其它部件质量，认为换能器的总质量为两连杆和压电堆质量之和，为8 g。因此压电换能器的质量和拉伸刚度均与原杆件不同，而且不能承受弯曲。可以预见，将杆件替换为换能器将会对结构动力学特性产生影响，但由于本文方法只需替换极少量杆件作为换能器，因此固有频率和振型的变化可以忽略不计，这一点可以在下文中看出。

图3 压电换能器示意图Fig.3 Sketch of the piezoelectric transducer

在本文提出的方法中，每个压电换能器连接一个独立的LR电路。图4给出了只采用一个压电换能器时，机电耦合系统的示意图。采用拉格朗日-麦克斯韦方程建立该系统的动力学方程。原结构的动能T、势能V、分路中电感的磁能Wm、压电换能器中的电能We以及耗散函数P分别为

(1)

式中：[M]s为质量矩阵；[K]s为刚度矩阵；{x}为结点位移矢量；q为分路电量；L为分路电感；C为压电堆等效电容；k为压电堆机电耦合系数；n为压电堆所包含压电片的个数；d33为压电应变系数；{b}为压电换能器位置矢量；L为分路电阻；Ka/(1-k2)为压电堆开路刚度。

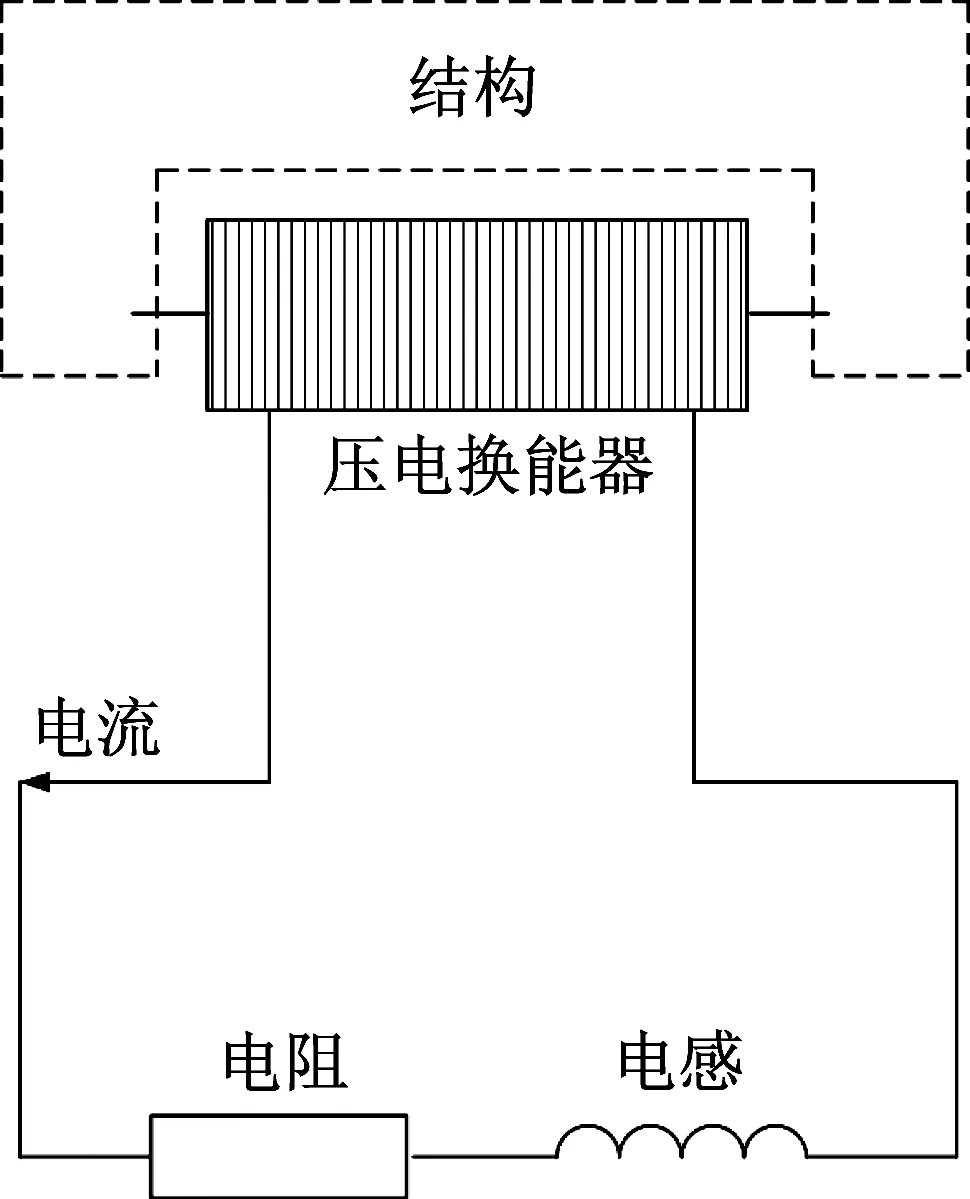
图4 机电耦合系统示意图Fig.4 Sketch of the electro-mechanical coupled structure

利用拉格朗日-麦克斯韦方程建立系统的动力学方程

(2)

写成矩阵形式

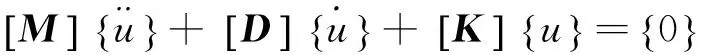
(3)

其中,

(4)

当使用l个压电换能器时，式(4)中的各矩阵分别为

[K]=

(5)

2 多模态独立模态压电分流控制方案

在独立模态压电分流控制中，每阶模态由独立的压电换能器及其连接的分流电路来控制。为了说明该控制方法中各阶模态控制的独立性，首先要考虑替换杆件为压电换能器对结构带来的影响。虽然压电换能器的特性与原杆件不同，但由于换能器数量等于需要控制的模态数量，而实际应用中往往只需控制少量低阶模态，因此该方法只需替换极少量杆件作为换能器，并不会显著改变原结构的模态。

接下来考虑添加分流电路带来的影响。分流电路主要对结构的阻尼特性产生影响，这一点可以从下文控制前后固有频率和阻尼比的变化看出。由于谐振电路的通频带很窄，选频能力强，特定模态对应的分流电路只对该阶模态的阻尼产生效果，而几乎不会影响其它模态的阻尼。

综合以上两点可以看出，对于已设计完成的多模态压电分流控制系统，移除现有的压电分流电路或者为其它阶模态添加新的压电分流电路，都不会对保持不变的模态的附加阻尼效果产生明显影响。

为了达到最佳的控制效果，对于给定模态，首先需要为压电换能器配置最佳的位置，之后需要对分流电路的参数进行调整使其匹配所要控制的模态。

2.1压电换能器位置优化

若只考虑第i阶模态，方程式(2)截断为

(6)

式中：xi为第i阶模态的坐标；ωoi为压电换能器处于开路状态时，第i阶模态的固有圆频率；λi为对于第i阶模态，机电耦合的强度，可定义为

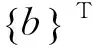
(7)

式中，{φi}为第i阶模态的振型。λi值越大，第i阶模态的能量转换入压电换能器的能量就越多。可见，对于第i阶模态对应的换能器，应使其替换具有最大λi值的杆件。由于本方法中只需替换极少量杆件为换能器，因此替换后结构的振型几乎不受影响，可以使用原结构的振型计算。实际上，λi值与模态应变能有关。第i阶模态的模态应变能为

(8)

因此模态应变能可以作为压电换能器位置优化的指标。图5给出了控制前三阶模态时的换能器位置配置。

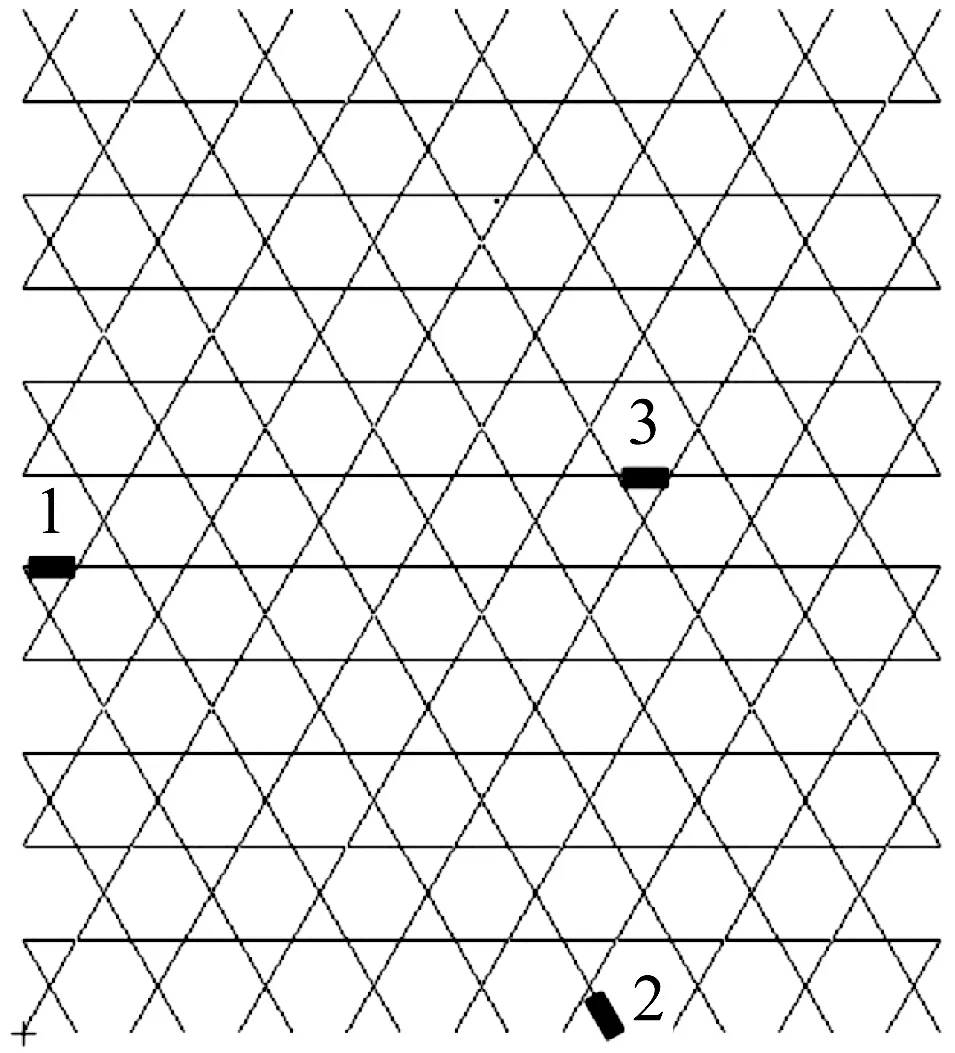
图5 前三阶模态换能器的位置，数字1～3代表了各换能器所控制的模态Fig.5 Locations of modal transducers of modes 1-3, the number 1-3 represents the mode to be controlled by each transducer

由于压电换能器的质量和刚度与原杆件不同，且不能承受弯曲，需要讨论布置换能器对结构动力特性的影响。下面研究将图5位置的杆件替换为压电换能器，且换能器处于开路状态时，结构模态固有频率和振型的变化。计算可得替换短路状态的换能器后，结构的前三阶固有频率为：297 Hz，507 Hz和550 Hz。显然，固有频率的改变完全可以忽略。换能器处于开路状态时，结构的模态仍然为实模态，因此可以直接与未布置换能器时的模态振型进行比较。为了量化振型的变化，引入以下振型重合度的概念

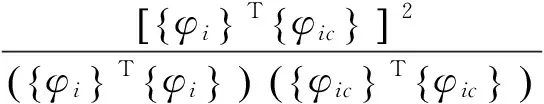
(9)

式中：下标i为模态的阶数；{φi}为替换换能器前第i阶模态的振型；{φic}为替换后第i阶模态的振型。χi值可以量化控制前后振型的差异，该值在0～1，取值越接近1，说明模态振型的变化越小。计算可得替换换能器前后，前三阶模态的重合度分别为0.999 98，0.999 97，0.999 96。因此可以认为模态振型未发生变化。

2.2压电分流电路参数优化

与动力吸振器类似，谐振分流电路的核心问题是对参数进行调谐。文献[13]中研究了小型桁架结构的压电分流控制，并给出了对于第i阶模态的自由振动，最优化的电感L和电阻R值

(10)

式中，ωsi为压电换能器处于短路状态时，第i阶模态的固有圆频率。而

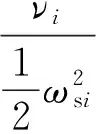
(11)

式(11)是压电换能器在第i阶模态中模态应变能的百分比。使用式(10)可以得到前三阶模态的电感和电阻值，代入式(5)并数值求解特征值问题，可以得到各阶模态(含原结构机械模态和附加的三阶“电模态”)的频率和阻尼比，表2给出了前三阶机械模态和前三阶电模态的固有频率和阻尼比，可以看出机械模态的固有频率与附加分流电路之前变化很小，但机械模态阻尼比很小，原因在于这三阶分流电路模态的固有频率与其对应的机械固有频率相差较多。

表2 采用式(10)得到的电路参数时的前三阶机械模态及前三阶电模态Tab.2 The first three mechanical modes and all three electrical modes using shunt parameters obtained by (10)

造成以上结果的原因在于式(10)给出的公式是由单自由度系统推导出的，当结构规模较大时，机械模态部分将会对电模态产生较大影响，使耦合后电模态的固有频率偏离所期望的调谐值。计算发现，调整电阻值几乎不会影响频率特性，因此本文利用各阶谐振电路的独立性，提出了一个简单可行的优化方法。

首先利用式(10)计算出的电阻和电感值计算出系统所要控制的机械模态和对应的电模态的频率和阻尼比，之后对每阶模态逐一用试探法进行优化，先调整电感值使电模态和对应的机械模态的固有频率充分接近，再调整电阻值使阻尼比达到最大。为了说明这个方法，下文给出了1～3阶模态分流电路的逐一优化过程：

(1) 电感L1优化后，第一阶电模态的固有频率f1=295 Hz。

(2) 电阻R1优化后，f1=292 Hz，第一阶机械模态的阻尼比ξ1=0.029。

(3) 电感L2优化后，f1=292 Hz，ξ1=0.029,f2=507 Hz。

(4) 电阻R2优化后，f1=292 Hz,ξ1=0.029,f2=504 Hz,ξ2=0.023。

(5) 电感L3优化后，f1=292 Hz,ξ1=0.029,f2=504 Hz,ξ2=0.023,f3=547 Hz。

(6) 电阻R3优化后，f1=292 Hz,ξ1=0.029,f2=504 Hz,ξ2=0.024,f3=546 Hz,ξ3=0.021。

从以上过程中可以看出电阻的调整不会影响已调谐好的电路模态频率，而且对任一阶模态的分流电路参数进行调整时，对其他模态的影响很小，正因如此，模态分流电路的参数才可以逐一优化，又因为电感和电阻可以分开优化，该优化问题转化为一系列的一维优化问题，可以采用试探法。

采用该方法优化后的前三阶机械模态和前三阶电模态的固有频率和阻尼比列入表3，可以看出前三阶分流电路模态的固有频率与其对应的机械模态固有频率较为接近，因此阻尼比都非常可观。另一方面，机械模态的固有频率与控制前相比几乎没有变化。

谐振分流电路通频带较窄虽然会使各分流电路之间较为独立，但也会造成一旦系统频率发生变化，控制的效果会大大下降。不过，在发现系统动力特性发生变化后，可以采用本节的试探优化法重新进行调谐。

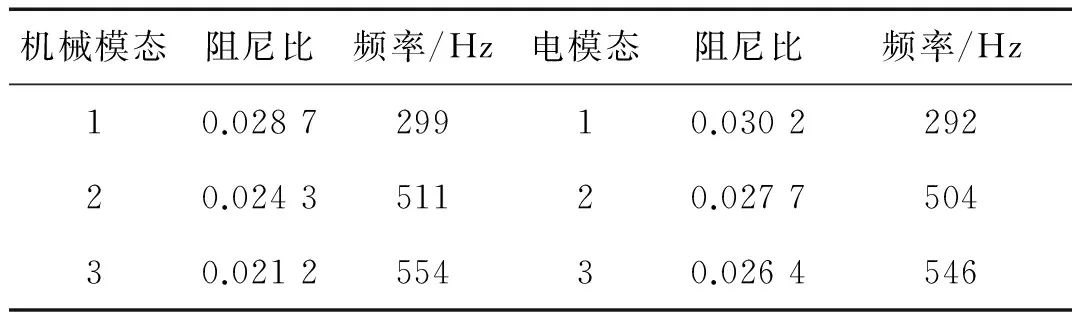
表3 采用文中方法得到的电路参数时的前三阶机械模态及前三阶电模态Tab.3 The first three mechanical modes and all three electrical modes using shunt parameters obtained by the method in this paper

3 数值分析

假设原结构的阻尼为比例阻尼，即阻尼矩阵满足

[D]s=α[M]s+β[K]s

(12)

式中：α=23.5；β=3.96×10-6。在图2的箭头处施加一个1 000 N的脉冲激励，并观察该点竖直方向自由振动的响应情况。图6给出了原结构以及控制1～3阶模态时的响应情况，可以看出控制后响应的衰减明显加快。

为了独立考察各阶模态振动衰减的情况，对两种情况下的时间历程进行短时傅里叶变换，图7和图8分别给出了无控制和控制前三阶模态时脉冲响应的短时傅里叶变换。可以看出前三阶模态的衰减明显加快(第二阶和第三阶模态较为接近)，而其它阶模态没有明显变化。

为了说明各阶模态谐振电路的独立性，在控制1～3阶模态的基础上，再增加一个压电换能器用于控制第四阶模态，保持前三阶模态分流电路的参数不变。此时换能器的配置如图9所示，图10给出了此时脉冲响应的短时傅里叶变换。可以看出与图8相比，第四阶模态的衰减明显加快，而其它阶模态的衰减特性基本不变。

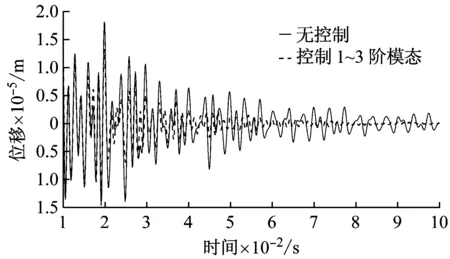
图6 无控制和控制1～3阶模态时脉冲激励的响应Fig.6 Response under the impulse excitation of the structure without control and with mode 1-3 controlled

图7 无控制时脉冲响应的短时傅里叶变换Fig.7 Short-time Fourier transform of impulse response without control

图8 控制1～3阶模态时脉冲响应的短时傅里叶变换Fig.8 Short-time Fourier transform of impulse response with mode 1-3 controlled

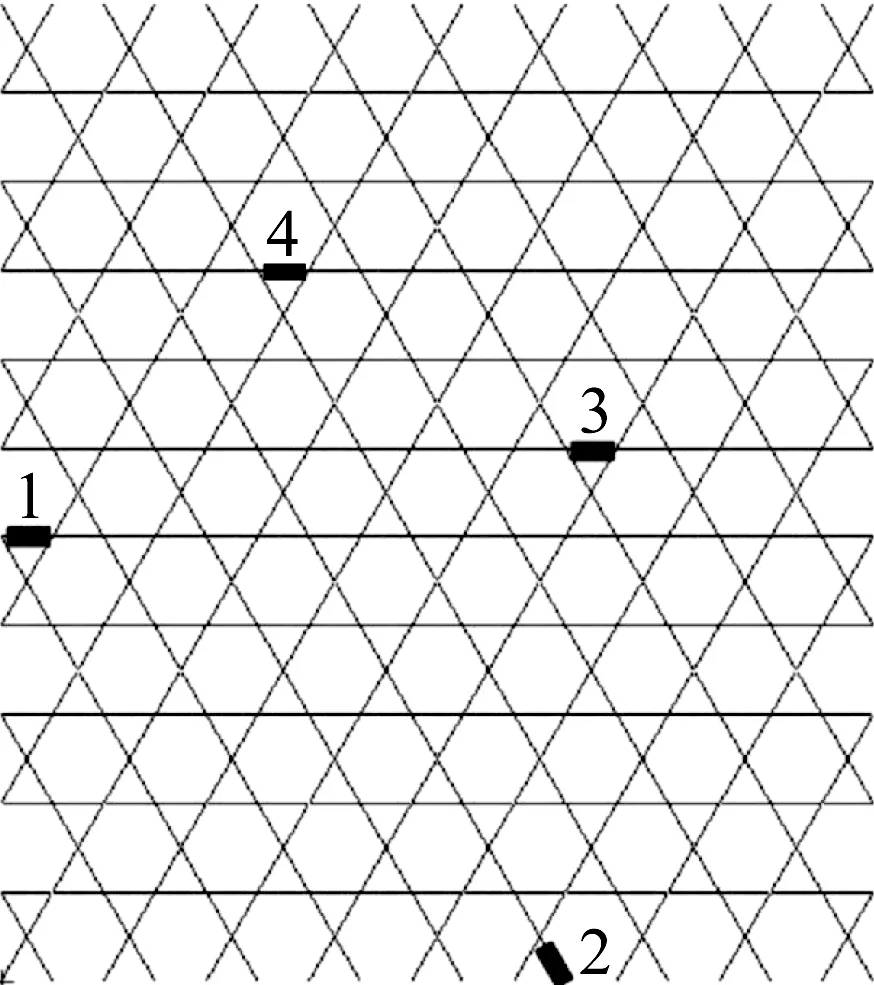
图9 前四阶模态换能器的位置，数字1～4代表了各换能器所控制的模态Fig.9 Locations of modal transducers of modes 1-4, the number 1-4 represents the mode to be controlled by each transducer

图10 控制1～4阶模态时脉冲响应的短时傅里叶变换Fig.10 Short-time Fourier transform of impulse response with mode 1-4 controlled

4 结 论

本文提出了一种独立模态空间压电分流振动控制的方法，并给出了一种实用的电路参数优化方法，可以实现Kagome夹心板的多模态自由振动控制。算例表明该方法非常有效，而且各阶模态的控制相互影响很小。

本文中只研究了自由振动的控制情况，对于强迫振动，控制的目标不再是特征值问题，而是频响函数。针对强迫振动的分流电路参数优化是今后的研究目标之一。为了将该方法向一般结构推广，对称结构重频和密频的问题不可回避，而本文的方法尚未考虑该问题。最后，该方法的有效性还需要实验进行验证。

[1] WICKS N, HUTCHINSON J W. Sandwich plates actuated by a Kagome planar truss[J]. ASME Journal of Applied Mechanics,2004,71(5):652-662.

[2] GUO X, JIANG J. Passive vibration control of truss-cored sandwich plate with planar Kagome truss as one face plane[J]. Science in China-Technological Science, 2011, 54(5):1113-1120.

[3] GUO X, JIANG J. Optimization of actuator placement in a truss-cored sandwich plate with independent modal space control[J]. Smart Materials and Structures, 2011, 20(11):115011.

[4] 彭海波，申永军，杨绍普. 一种含负刚度元件的新型动力吸振器的参数优化[J].力学学报,2015,47(2):320-327.

PENG Haibo, SHEN Yongjun, YANG Shaopu. Parameters optimization of a new type of dynamic vibration [J]. Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):320-327.

[5] 徐赵东. 黏弹性减震控制结构随机状态反应分析[J]. 振动与冲击, 2008,27(1):37-39.

XU Zhaodong. Random state response analysis for a viscoelastic earthquake-mitigating structure[J]. Journal of Vibration and Shock，2008,27(1):37-39.

[6] 徐亚兰，陈建军. 空间范数在压电柔性结构振动控制中的应用研究[J]. 工程力学, 2013,30(10):1-4.

XU Yalan, CHEN Jianjun. Research on vibration control of piezoelectric flexible structures based on spatial norms[J]. Engineering Mechanics,2013,30(10):1-4.

[7] 李彦，何琳，褚福磊. 磁流变阻尼器实验建模及模糊半主动振动控制[J]. 振动与冲击, 2009,28(11):91-95.

LI Yan, HE Lin, CHU Fulei. Modeling of MR-fluid damper and fuzzy semi-active vibration control strategy [J]. Journal of Vibration and Shock,2009,28(11):91-95.

[8] 杨智春，孙浩.基于拓扑优化的压电分流阻尼抑振实验研究[J]. 振动与冲击, 2010,29(12):148-152.

YANG Zhichun, SUN Hao. Experiments of piezoelectric shunt damping for vibration control with topology optimization[J]. Journal of Vibration and Shock,2010,29(12):148-152.

[9] 张文群，张萌，吴新跃.负电容压电分流阻尼系统的能量耗散特性[J]. 振动与冲击, 2008,27(10):70-74.

ZHANG Wenqun, ZHANG Meng，WU Xinyue. Energy dissipation performance of a piezoelectric shunted system with negative capacitance[J]. Journal of Vibration and Shock,2008,27(10):70-74.

[10] JI H, QIU J, CHENG J, et al. Application of a negative capacitance circuit in synchronized switch damping techniques for vibration suppression[J]. Journal of Vibration and Acoustics,2011, 133(4)：041015.

[11] WU S Y. Method for multiple mode piezoelectric shunting with single PZT transducer for vibration control[J]. Journal of Intelligent Material Systems and Structures,1998, 9(12):991-998.

[12] ALESSANDRONI S, DELL′ISOLA F, PORFIRI M. A revival of electric analogs for vibrating mechanical systems aimed to their efficient control by PZT actuators[J]. International Journal of Solids and Structures, 2002,39(20): 5295-5324.

[13] PREUMONT A, DE MARNEFFE B, DERAEMAEKER A, et al. The damping of a truss structure with a piezoelectric transducer [J]. Computers and Structures, 2008，86(3/4/5): 227-239.

Multi-modepiezoelectricshuntvibrationcontrolofaKagomesandwichpanel

GUO Kongming, XU Yalan

(Research Center of Applied Mechanics，School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, China)

Aiming at realizing the multi-mode vibration control on a Kagome sandwich panel, a kind of independent modal piezoelectric shunt vibration control method was proposed. The finite element model of the structure coupled with piezoelectric transducers was established, then the proposed vibration control strategy on the Kagome sandwich panel was described in detail, while a practical multi-shunt circuit parameters optimization method for mitigating the free vibration was also presented. The results show that the control method proposed can significantly improve the damping characteristics of the Kagome sandwich panel structure, and accelerate the attenuation of free vibration. At the same time, the piezoelectric shunt circuits have good independence between each other.

Kagome sandwich panel; multi-mode vibration control; piezoelectric shunt vibration control；free vibration

O328; V214.3

A

10.13465/j.cnki.jvs.2017.19.009

国家自然科学基金青年科学基金项目(11502183); 陕西省自然科学基础研究计划面上项目(2016JM1021); 博士后基金面上项目(2016M592750)

2016-06-08 修改稿收到日期：2016-07-29

郭空明 男，博士，讲师，硕士生导师，1985年生