“互联网+”时代农村物流配送中心选址的优化方案设计

杨叶勇

基金项目：江苏省教育厅哲学社会科学研究基金资助项目“苏南地区应急物流供应链的构建与运行机制研究”（批准号2013sjb6300091）；职教类青年专项课题“基于双维视角的‘现代学徒制参与者研究”（课题编号SYKJ15D14）

中图分类号：F252 文献标识码：A

内容摘要：本文简要概述了农村物流配送中心选址的内容及原则，对物流配送中心选址的目标以及选址决策流程进行具体分析，基于成本最小化视角设计了农村物流配送中心选址的优化模型。在此基础上，利用启发式算法对运行步骤进行细致分析，最后使用案例算法得到农村物流配送的最佳选址方案。

关键词：“互联网+” 农村物流 配送中心 选址 模型设计

“互联网+”时代下农村物流配送中心选址要义、目标与决策流程

一般而言，“互联网+”时代下农村物流配送中心选址应遵循以下基本原则：第一，经济性原则。农村市场经济潜力巨大，流通企业在入驻农村规划配送中心選址时，以盈利性为基本原则，即综合考量费用的最低成本。这类成本包括了设施成本、交通工具与运输成本以及仓储等费用。同时，物流配送中心选址的确定位置，对之后配送时间、服务质量都会产生较大影响。因而，遵循经济性原则规划配送中心选址，能够更好地开展农村市场的竞争。第二，适应性原则。在农村区域规划物流配送中心，还应与当地的政策、物流运输等方面结合，与当地技术发展水平、区域分布情况以及交通运输承载力等协调统一发展。第三，战略性原则。选择最佳的物流配送中心，需要从农村区域的大物流系统出发，遵循当地整体发展战略。特别是在“互联网+”时代背景下，需要从全局层面考虑，局部服从整体，短期利益服从长期利益，为拓展农村市场奠定基础条件。

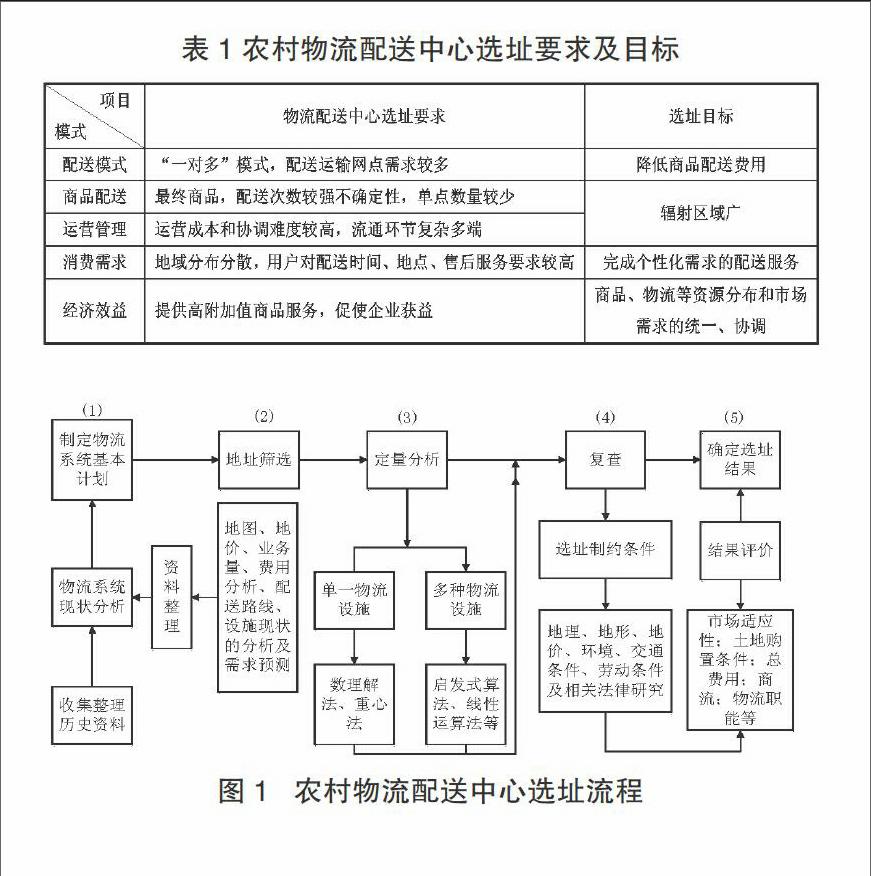
农村物流配送中心是联系城乡商贸流通的重要节点，其运作模式特征在于它并不是以商品生产为运作的社会组织，而是从各类生产商、批发商等手中汇聚商品资源，然后进行分类、配送等集约化的行为，进而实现最合理的利用物流网络资源、降低商品流通成本的目的。因而，受农村交通运输条件、商品资源分布以及市场需求因素的影响，农村物流配送中心的选址规划设计在同一区域不同节点、不同的布局方案，所产生的经济效益与社会效益可能会有较大的差异。合理布局选址方案的最主要目标在于，为用户提供高质量、全方位的周到服务，降低流通成本，进一步实现社会效益与经济效益的协调与统一。所以，商家在农村物流配送中心选址过程中（见表1），应根据配送模式、配送物品、组织管理、顾客需求以及经济效益的选址要求，实现与之对应的目标即流通费用较低、服务质量水平较高、辐射区域广泛以及社会效益高等。其中，流通费用低包括在规划物流配送中心选址时，考虑到基础设施成本与运营成本的总成本最低；服务质量水平较高是指所选的物流配送中心，应保证配送商品及时、完好地送达客户；辐射强及社会效益高是指农村物流配送中心选址应从所选区域的物流大系统出发，使得选址区域的物流资源与市场需求、商品资源分布能够达到高度协调与统一，适应地方经济发展的实际情况。

选择合理的农村物流配送中心地址，能够最大限度降低流通企业成本、提升经济效益。配送中心选址的决策过程主要包括以下几个环节（见图1）：首先，决策者通过收集整理历史资料，分析当地物流系统现状；经过资料整理，细致分析当地地价、业务量、费用、配送路线、设施现状等资料，进而开始定量分析，由此制定物流系统基本计划。其次，在对配送中心选址时，还应进行算法科学评估。若对单一配送中心进行选址，可采用数理解法、重心法；而针对多个配送中心进行选址时，可采用启发式算法、线性运算法等。再次，决策者选出最佳选址算法时，需要进一步对所得结果进行复查。复查就是要对农村物流配送中心的选址约束条件进一步细分。此时，决策者应明确建立配送中心成本高低、必要性，还应根据物流系统基本计划，确定所需要了解的基本条件，包括地理环境、交通条件、劳动条件、相关法律等，以缩小选址范围。在此基础上，对上述影响因素赋予一定权重，并使用加权算法对结果进行计算、核查。如所得数值通过核查步骤，那么该选项为最佳选址之一；如不符合原计算结果，需要返回上一步骤重新运算，直至循环结果同一。最后，需要决策者综合服务质量、市场生产与消费资料、土地价格等，对所得结果进行评价，考察其可行性、现实意义及实用性，进而得到最佳的农村物流配送中心选址。

农村物流配送中心选址的优化模型构建

农村物流配送中心选址是否合理，将直接影响到农产品配送活动是否高效。科学合理建设配送中心，不仅可降低配送中心运营成本，还可推动商品产销间的最佳协调，进而保持商品流通渠道的畅通。在分析农村物流配送中心选址的决策流程基础上，还需运用模型理论与实际案例进行具体探讨。因而，本文将总费用最低化作为基本目标，综合考虑农村物流配送中心位置、仓储、交通等因素，进行了其选址最优化模型目标函数的构建。

（一）模型基本假设与变量选取

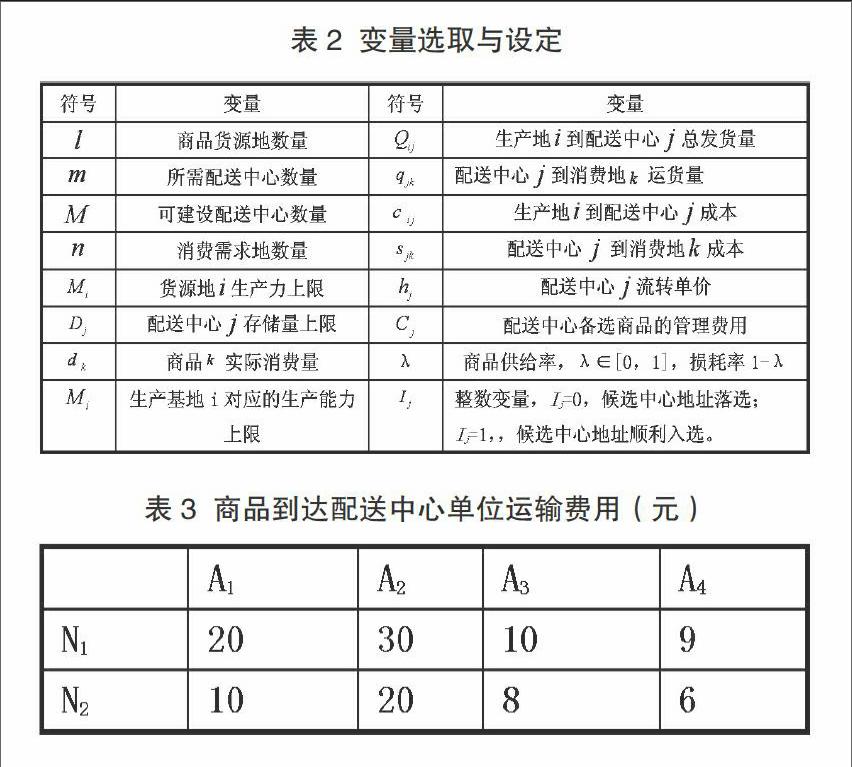
现进行如下假设：选定若干农村物流配送中心的候选区域，并在选定区域内进行最优筛选；只有一个物流配送中心提供消费市场区域的已知需求量；已知商品在农村地区的运输费用，且运送地和配送中心之间距离和运输费用呈正比关系；假设在”互联网+”环境下，候选配送中心的基础设施费用、运营管理费用已知；假设运输速度为常量，且已选定的农村商品物流配送中心总体容量能够有效满足该区域的消费需求。同时，区域内的消费需求数量可以根据统计分析，即需求量是一个预测的外生常量。基于此，本文设定变量如表2所示。

（二）模型构建

从系统成本的最小化视角出发，设立“互联网+”时代下农村物流配送中心选址成本最小化模型构建，即：

（1）

公式（1）中，所包含的约束条件如下：第一，， i=1，2，…，l， j=1，2， …，m，该公式所要表述商品生产地受到实际生产能力的约束。商品货源地数量（l）与生产地到配送中心总货量的总和数量，要小于商品基地对应的生产能力的上限。在此条件下，商品数量的配送可与当地消费需求数量达到平衡状态。第二，，j=1，2， …，m ，该公式所要说明的是，商品配送中心j容量建设约束。即配送中心数量（m）与配送中心（j）到消费地（k）运货量的乘积，也就是总货量与商品生产基地对应生产能力的上限做比较。如超出这个能力，则不适宜将该地区作为物流配送中心。第三， ，j=1，2， …，m ，在考虑到商品配送中心供应能力时，配送中心数量（m）与配送中心（j）到消费地（k）运货量的乘积，与商品实际消费量（k）作比较。正常情况下，配送中心商品总货量应稍大于或等于实际消费需求量，才可以满足当地区域的消费需求。第四，，j=1，2， …，m ，在考虑商品配送中心建设数量时，配送中心数量（m）与整数变量（Ij）的乘积，与可进行的农村物流配送中心数量作为比较。只有当前者小于或等于可建设的配送中心数量时，该地区入选作为配送中心才有最大的社会经济效益。第五，当上述约束条件满足 Qij≥0， qjk≥0， cij≥0，sjk≥0 ，且相应变量限定于条件 i=1，2，…，l， k=1，2，…，n，j=1，2，…，m 时，成本最小化（Cmin）模型运算才真正有意义。endprint

（三）模型的运算与求解

传统算法中，NQ-difficult是一种无法获得精确解的问题，而配送中心选址优化模型的求解过程过于复杂，类似于该问题的解答。为此，需要借助一种更为精简的算法，更好对农村物流配送中心选址模型进行运算与求解，此时的启发式算法成为比较好的选择。具体来说，设定在m个候选区域内每次所选的结果组成N个组合集，即 CNm。在该集合中，包括候选区域的配送中心下标集合为V。随后，应用启发式算法对农村物流配送中心组合情况进行求解，将每个组合集讨论完后，计算终止。具体算法步骤如下：

Step1：let U=V。计算出组合集中候选区域的中心容量上限为 ；鉴于配送中心容量上限需要满足该区域的消费需求，还需要验证与比较情况，如若前者大于或等于后者，那么该条件满足，组合进入下一步的运算；否则删除该组合，继续分析下一组。

Step2：计算， J={jmin[cij+sjk]}，j∈U

Step3：利用单纯形方法求解下列线性规划问题：

目标函数： （2）

约束条件：

（3）

利用图上作业法在约束条件（3）的情况下，对目标函数（2）进行运算，获得线性规划的最优解：

{Qij+qjk}（ i=…l； j=…m； k=…n） （4）

Step4：求解农村物流配送中心j配送容量 Qi=∑Qij， j∈U分析是否满足 λQj≤Dj，j∈U条件，如若满足，进行下一步；不满足则删除该组合，分析下一组合。

Step5：let U=U-1，直到出现U=φ结果，该运算结束。在U=φ结果的条件下，选择出符合条件的组合，对之求解，获得Cmin对应值。所选组合即为成本运行最低、配送服务质量较高以及社会经济效益最大化的最终结果。

（四）选址模型的仿真案例

假设，N1和N2为两个不同的商品货源地，其日供货量分别为70吨和50吨，可分别供应5个消费区Y1…Y5，并假定其货物需求量为固定数值。商品货源地周边则存在4个物流配送中心以供选择，分别为A1…A4，其建设费用分别为100万、80万、120万、160万，存储最大量为50吨、40吨、60吨、80吨，商品的流转单位为10元/吨、15元/吨、8元/吨、6元/吨。所建物流配送中心的单位商品流转量成本，是依据该物流中心最大存储量和其建设费用比来计算，并在商品货源地和消费者之间进行流转。其中，农村物流配送中心的选址关键在于，能否利用最佳计算机编码进行选择。在本算例中，有4個物流配送中心、2个供应商与5个消费区，只在4个候选区域中选择一个目标作为配送中心。故本算例规模较小，在计算商品到达配送中心的单位运输费用时，可采用二进制编码运算。通过以上假设并运算得到表3单位运输费用值，在N1和N2两个货源地到4个配送中心运输费用大小为：A1>A2>A3>A4。

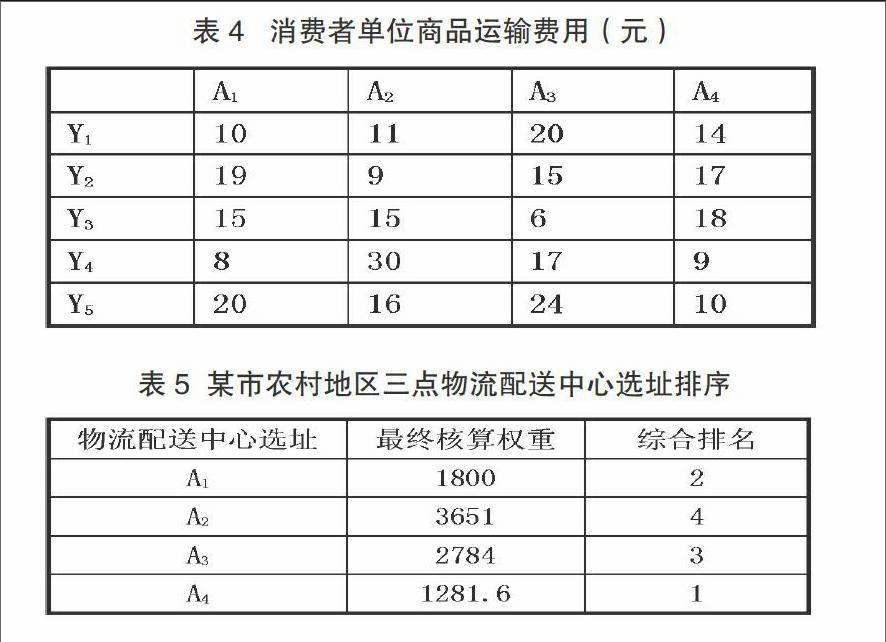
同理，商品经由配送中心到达消费者手中的单位运输费用则如表4所示，A1、A2、A3、A4与Y1、Y2、Y3、Y4、Y5的对应费用所得比较为：72、81、82、68即A4

最后，依据上述A1、A2、A3、A4案例，依据最终权值矩阵得到最终核算权重：

A1点总成本：0.1*20*10*10+0.22**20*10*10+0.25**20*10*10+0.33**20*10*10=1800

A2点总成本：0.2*30*20*11+0.23*30*20*9+0.25*30*20*15+0.2*30*2*5=3651

A3点总成本：0.4*10*8*20+0.3*10*8*15+0.5*10*8*6+0.4*10*8*17=2784

A4点总成本：0.2*9*6*14+0.1*9*6*22+0.15*20*6*26+0.2*9*6*9+0.2*19=1281.6

将最终所得总成本顺序进行排序，得到表5结果。通过表3、表4计算数值以及表5的选址排序可知，A4综合优先级排名最高。因而，选择A4为农村某区域物流配送中心选址的最佳方案。具体而言，经过对某市农村地区四点位置的最小成本模型、启发式算法、仿真案例运算分析发现，农村物流配送中心选址应综合配送中心到消费区域的运输费用、消费者单位商品运输费用以及综合经济效益的变量进行考量。在算例验证过程中，A1、A2、A3、A4四个地区总得分比较，最终核算权重分别为1800、3651、2784、1281.6。可见，A4点最终权重得分较为明显，成为最后选址的最佳地点。由此判断发现，本文所采用的算法过程所得结果，与前文最小化成本演算理论结果相近，进而也进一步验证上述成本最小化算法的可靠性。

参考文献：

1.冯佳.基于C2C电子商务模式的农村物流发展体系构建[J].商业经济研究，2015（8）

2.李鹏.流通配送中心选址的模型研究——以生鲜食品为研究对象[J].商业经济研究，2016（12）

3.张婷婷.有竞争的物流配送中心选址模型研究[J].物流科技，2014（11）