节理面直剪试验及抗剪强度参数优化分析

李泽栋， 程 述， 柯长仁， 任鸿飞

(1 湖北工业大学土木建筑与环境学院， 湖北 武汉 430068； 2 无锡城市发展集团， 江苏 无锡 214000)

节理面直剪试验及抗剪强度参数优化分析

李泽栋1， 程 述2， 柯长仁1， 任鸿飞1

(1 湖北工业大学土木建筑与环境学院， 湖北 武汉 430068； 2 无锡城市发展集团， 江苏 无锡 214000)

基于不同粗糙度人工节理面直剪试验，采用最小二乘法一元线性回归和抛物线回归两种方法，对其抗剪强度参数优选分析。结果表明：利用最小二乘法一元线性回归处理大样本数据、线性关系的数据十分有效。

直剪试验； 强度参数； 最小二乘法

随着岩石力学理论的不断深入，对于节理面的研究取得了显著的发展，但其抗剪强度参数的不确定性始终都是学者研究的难点。由于大量的研究试验基本上采用室内岩体试验，与实际岩质工程中的诸多因素都不符，因而如何合理并切合实际地选取工程所涉及的强度参数尤为重要。

在岩体力学参数优化设计研究方面，李华晔[1]等采用随机—模糊分析法对其强度参数进行优化设计，并运用到实际工程中。符文熹[2]等考虑岩石的渐变性特征，提出了岩体变形参数渐变取值模型，并通过验算李家峡水电站监测资料，为岩体工程的力学参数分析提供了理论指导。本文通过对花岗岩取样，人工加工成平直形和起伏形两种不规则形状的节理面(其中平直形节理面为小样本数据，起伏性节理面为大样本数据)，将两种不同形状的节理试件在不同的法向应力下进行不同的直剪试验，得出相应的峰值抗剪强度，然后采用最小二乘法线性回归和抛物线回归两种分析方法进行抗剪强度参数优选，并计算相关系数[3]，最后通过部分试验数据验算比较两种方法的适用性。

1 试验研究

1.1试件制备

本试验所使用的花岗岩样品来自于贵州毕威高速公路乌木铺高边坡。由于获得天然节理面难度较大且不易保存和运输，故采用人工浇注的素混凝土制作节理试样，试样浇筑料度等级为42.5标号的快硬水泥，浇筑料的配料设计比为：m(水泥)∶m(掺有少量砾石的干粗砂)∶m(水)=1∶1.5∶0.4，养护28 d达到足够强度，同时保证尽量减少水分散失。节理面受剪面尺寸100 mm×100 mm，节理试样见图1，受剪面上、下岩石的厚度约为受剪面尺寸的一半，使受剪面平行于模盒边框面，且高出模盒边框5 mm，同时试样剪切方向与模盒边框的方向一致。

1.2直剪试验设计及结果

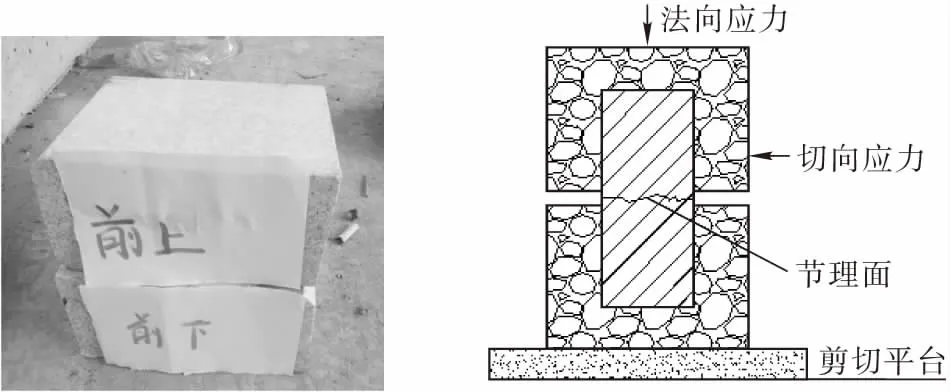
图 1 花岗岩节理试样 图 2 节理剪切受力方向

本文进行了在不同法向荷载作用下花岗岩不同形状节理面的直剪试验，按荷载控制方式施加法向荷载直至预定值，由于本文重点在于分析优化节理面抗剪强度参数。与节理面起伏角度、粗糙度、试验中的剪切速率等影响因素均无太大关联，只将节理面粗糙度分为平直形(小数据)和起伏形(大数据)两种形状描述。花岗岩节理面设定不同法向应力，施加水平向左的切向应力，切向加载增加速率为0.5 mm/min，花岗岩节理剪切受力方向如图2所示，同时设定最大剪切位移以20 mm为定值。将制备好的样品放入剪切盒里，确保上下两块按照事先做好的标记吻合良好,并保持稳定，同时避免节理面发生相对移动从而导致破坏。试验时先通过水平千斤顶预加切向应力，然后通过垂直千斤顶分级施加预定的法向应力，测得破坏时的峰值抗剪强度并记录。直剪试验结果见表1。

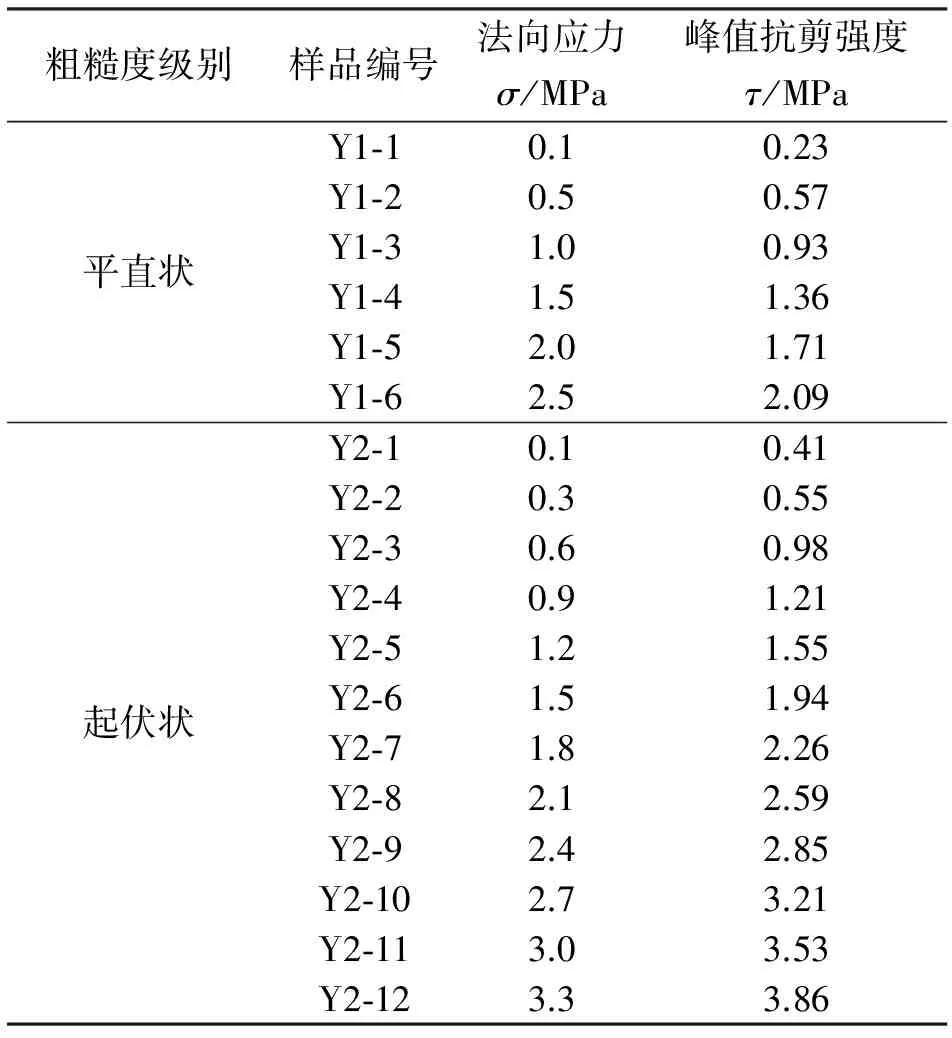
表1 节理样本试验结果

2 节理面抗剪强度参数优化分析

2.1回归分析方法

回归分析法是在统计学的基础上，了解两个或多个变量间是否相关、相关强度，并建立数学模型。在对各种复杂且特殊的岩体工程设计分析时，由于实际环境和试验样本测定的局限性，只能通过对实验参数的回归分析，得出函数关系，近而大致估算岩体参数。岩体节理面抗剪强度参数数据回归分析方法中，包括经验类比法、点群中心法、优定斜率法、可靠度方法[4]、最小二乘法、随机—模糊法[5-7]。然而岩石节理面的力学特性具有很大的变异性，空间分布的不确定性使得其具有极大的模糊性，采用最小二乘法和随机—模糊法是很好的分析方法。由于最小二乘法适合于在样本容量小于变量个数的情况下建立回归函数，其统计特性具有一致的、无偏的、有效的特征，且计算方便简单，本文主要针对最小二乘法线性回归和抛物线回归两种分析方法进行抗剪强度参数优选分析。

2.2抗剪强度参数最小二乘法一元线性回归分析

最小二乘法一元线性回归分析主要是处理变量法向应力σ和峰值抗剪强度τ之间的关系，其数学函数的基本形式如：y=a+bx。根据微分学中求极值原理满足如下方程：

(1)

运用最小二乘法一元线性回归处理节理面抗剪参数基本原理是试验数据点到回归方程的垂直距离的平方和最小，节理面抗剪强度参数优化分析计算过程如下:

(2)

(3)

对抗剪强度参数线性回归分析采用莫尔一库仑强度曲线，函数表达式如下：

τ=σtanφ+c

(4)

将式(3)、(4)整合得出一元线性回归方程各项变量如下公式：

(5)

(6)

节理面法向应力和峰值抗剪强度数据分别计算求值，其计算过程见表2。

表2 计算数据 MPa

平直状人工节理面(小数据)最小二乘法一元线性回归方程表达式：

τ1=0.798σ1+0.154

(7)

起伏状人工节理面(大数据)最小二乘法一元线性回归方程表达式：

τ2=1.089σ2+0.274

(8)

2.3抗剪强度参数最小二乘法抛物线回归分析

节理岩石是包含众多裂隙和缺陷的复合结构体，Griffith(1921)首次提出裂隙扩展引起材料破坏的条件，建立了Griffith裂纹模型。对节理面抗剪强度参数分析过程中，

可以引用Griffith强度理论

来描述岩石节理试样从受力到破坏的过程。本文主要考虑作用在节理面的二维应力状态，其满足

τi2=ασi+β

(9)

运用式(2)和(3)函数关系得出抛物线回归方程各向系数表达式[8]如下：

(10)

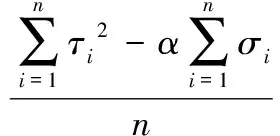
(11)

计算数据如表1、表2，则平直状人工节理面(小数据)最小二乘法抛物线回归方程为

τ12=1.27σ1-0.212

(12)

起伏状人工节理面(大数据)最小二乘法抛物线回归方程表达式：

τ22=3.863σ2-1.323

(13)

2.4数据验算及分析

节理面样本部分数据预测值与实测值对比分析见表3，将法向应力通过两个不同的回归方程得出相应的抗剪峰值抗剪强度，并与实测值对比。由表格可以看出一元线性回归法的相对误差很小，基本上控制在±3%以内，预测结果与实测结果基本一致，具有很高的精度。抛物线回归方程相对误差较大，预测结果与实测结果也具有一定的精度，但相比一元线性回归具有一定的局限性，数据最大误差11%。无论是一元线性回归方程还是抛物线回归方程，其大样本的起伏状节理面比小样本的平直状节理面的相对误差小许多，拟合精度高，适用性较强。

表3 样品预测值与实测值对比表

在对最小二乘法分析中，通常通过比较其相关系数r的值来检验该回归方程是否具有显著性问题，即实用价值。一元线性回归相关系数计算公式如下：

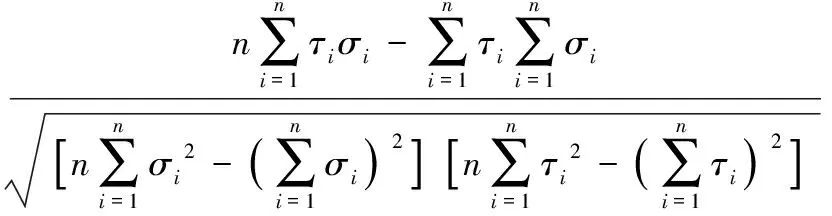
(14)

抛物线回归相关系数计算公式如下：

(15)

由式(14)、(15)得平直状(小样本)一元线性相关系数r=0.981，起伏状(大样本)一元线性相关系数r=0.999，平直状(小样本)抛物线相关系数r=0.967，起伏状(大样本)抛物线相关系数r=0.977。就相关系数而言，一般地利用最小二乘法的一元线性回归分析和由抛物线回归分析方法得到的方程的相关系数很接近，此即说明两者结果接近能比较真实地反映实验数据的情况。大样本数据相关系数比小样本相关系数大，且接近1，表明大样本数据所得出的回归方程更具有显著性。由以上四组数据可以看出其相关系数都接近1，表明试验数据法向应力与峰值抗剪强度具有明显的线性关系，在进行参数优化分析时更适合采用最小二乘法一元线性回归法。

两组节理面回归方程对比见图3、图4，可以看出采用最小二乘法一元线性回归方程能很好地反映实测数据点的情况，实测数据点总是均匀地分布在一元线性方程的两侧，因而能反映实测数据点的实际情况。而利用最小二乘法抛物线的回归曲线存在一定的局限性，从图上可以看出，在一定的范围内与实测数据接近，但随着应力的增大，实测点数据越来越偏离曲线。

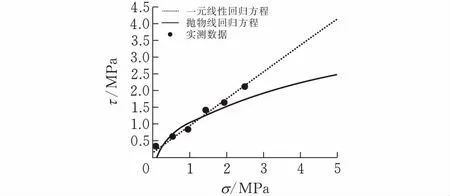
图 3 平直状节理面(小样本)回归方程对比

图 4 起伏状节理面(大样本)回归方程对比

3 结论

1)在对岩石节理面直抗剪强度参数进行优化分析时，采用最小二乘法所得的拟合方程具有一定的精度，分析原理简单，计算数据处理直观，可以广泛地应用到实际岩体工程中。

2)就本次试验而言，采用最小二乘法抛物线回归方程处理参数存在一定局限性，其相对误差呈现递增的趋势，要求在处理参数时就实际工程具体分析；而一元线性回归法所得拟合值与实测值基本吻合，相对误差在可控范围之内。特别是对于处理自身具有线性关系的数据，利用一元线性回归方程具有极大的优势。

3)处理节理面抗剪强度参数大样本实测数据中，两种回归方程的相对误差均比小样本数据的相对误差小，表明大样本数据所得出的回归方程更具有实用性。而其中最小二乘法一元线性的拟合方程结果合理，预测精度较高，具有较强的适用性，运用该方法分析此类问题十分有效。

[1] 李华晔，黄志全，刘汉东.岩基抗剪参数随机—模糊法和小浪底c、f值计算[J].岩石力学与工程学报，1997,6(2):155-161.

[2] 符文熹，尚岳全，孙红月等.岩体变形参数渐变取值模型及工程应用[J].工程地质学报，2001,10(2):198-203.

[3] 刘汉东.岩石力学参数优选理论及应用[M].河南：黄河水利出版社，2006.

[4] 杨强，陈新，周维垣.抗剪强度指标可靠度分析[J].岩石力学与工程学报，2002,21(6):868-873.

[5] 李胡生,魏国荣.用随机一模糊线性回归方法确定岩石抗剪参数[J].同济大学学报199321(3):421-429.

[6] 刘春.黄麦岭磷矿边坡岩体抗剪强度参数的随机一模糊法取值研究[J].岩石力学与工程学报.20052(4):653-656.

[7] 王鹏,李安贵,蔡美峰等.基于随机一模糊理论的岩石抗剪强度参数的确定[J].岩石力学与工程学报.200524(4):547-552.

[8] 王亦显.节理岩石力学参数测定[D].长沙：中南大学，1992.

[责任编校：张岩芳]

DirectShearTestandShearStrengthParametersOptimizationofJointPlane

LI Zedong1, CHENG Shu2, KE Changren1, REN Hongfei1

(1SchoolofCivilEngin.,ArchitectureandEnvironment,HubeiUniv.ofTech.,Wuhan430068,China; 2WuxiUrbanDevelopmentGroup,Wuxi214000,China)

The direct shear test of joint plane is the basis of the study on the failure mechanism and strength of rock mass. The strength parameters(cohesion and internal friction angle) optimization analysis is of great value for the dam foundation rock mass structure model, decision and construction optimization. The paper, based on the direct shear test of artificial joint surfaces with different roughness, conducted optimization analysis of shear strength parameters using two methods of least square regression and parabola regression. The results show that the least square method is effective to deal with the large sample data and the data of linear relationship.

direct shear test; dtrength parameters; least square method

2016-12-23

李泽栋(1993-)， 男， 湖北仙桃人，湖北工业大学硕士研究生，研究方向岩石力学与工程

1003-4684(2017)05-0019-04

TU458

A