由一个课本证明引发的教学思考
2017-11-03广东省江门市培英初级中学529000周小洋
广东省江门市培英初级中学(529000) 周小洋
由一个课本证明引发的教学思考
广东省江门市培英初级中学(529000) 周小洋
1、一个课本证明
人教版数学八年级下册在第18章第2节矩形的性质中,由“矩形的对角线相等”这一性质引导学生思考,并给出了直角三角形的一个性质的证明.
课本利用新学的矩形性质,对角线相等且互相平分,OB=由此得到直角三角形的一个性质(直角三角形斜边中线定理):直角三角形斜边上的中线等于斜边的一半.

图1
2、引发的教学思考
1.1 基于学生知识基础,探讨其他证法
对于本节内容,绝大多数老师都是沿用课本的证法.课本的证法虽然简洁,且与矩形的性质相关,但满足于一种证法,照本宣科,对培养学生数学思维并无益处.
求证两线段存在倍数关系,最常用的思路是“截长补短”(有些书称之为“割补法”),课本采用的是一种“补短法”.以下抛砖引玉,试着给出其他不同证明方法.
证法1上一节课学生已经学习了“中位线定理”,可以利用“中位线定理”证明,证明思路如下:取AB中点D,连接OD,因为OD是△ABC的中位线,所以OD//BC,所以∠ADO= ∠ABC=90°,又因为D为AB中点,所以OD垂直平分AB,所以
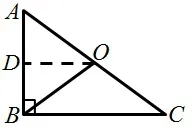
图2
证法2也可以先证明全等,后利用垂直平分线的性质,证明思路如下:过点O分别作OD⊥AB,OE⊥BC,因为 ∠ADO= ∠OEC=90°,∠AOD= ∠OCE,OA=OC,所以△ADO≌△OEC(AAS).所以OD=CE.易知,四边形DBEO是矩形.所以OD=BE=EC,又因为OE⊥BC,所以OE垂直平分BC.所以OB=OC=

图3
证法3 还可参照课本证法,向左对称作图,证明思路如下:根据对称可知,BC=BC′,∠1= ∠2. 又因为OA=OB,所以OB是△ACC′的中位线,所以OB//AC′,∠1= ∠3. 又因为 ∠1= ∠2,所以 ∠2= ∠3,所以

图4
证法4证明思维大致可以分为几何证明思维和代数证明思维.学生已经学习了“平面直角坐标系”、“勾股定理”两章,因此可以采用代数证明思维证明,证明过程如下:
以直角顶点B为原点,分别以直角边BC、AB所在直线为x轴,y轴 (如图所示),过O作OD⊥BC,设A(0,n),C(m,0).在Rt△ABC中,由勾股定理得:是AC中点,易知,在Rt△BOD中,由勾股定理得:

图5
对于八年级学生来说,以上四种证法所用的是前面学习过的知识,老师稍作点拨,学生还是有可能想到的;而对于进入中考复习阶段的九年级学生,还可以找到其他的证明方法,在此仅举一种.
证法5 利用“直径所对的圆周角是直角”证明,证明过程如下:因为AC是⊙O的直径,所以∠ABC=90°,显而易见,
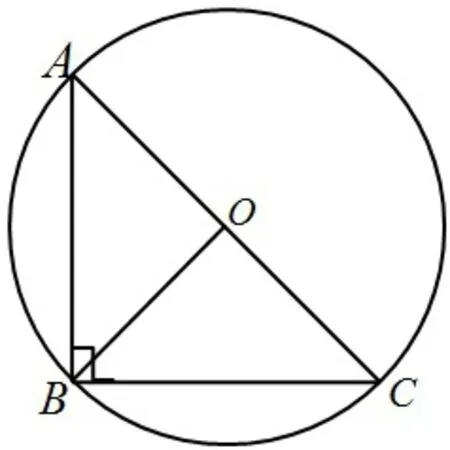
图6
1.2 基于以上证法,探讨如何改善教学
对不少学生来说,数学相比于其他科目,似乎更显枯燥,更加难学.而华人数学大师陈省身却给少年儿童题词“数学好玩”,这与我们很多人对数学的认识大相径庭.数学好玩,好玩在哪儿?数学的魅力在哪儿?如果我们数学老师不能回答好这些问题,那么培养学生的数学学习兴趣就无从谈起.
数学的魅力是多层面的,相比于其他学科,数学更加注重思维训练,你会惊讶于它思维的严谨、方法的灵活、结论的简洁.这就要求我们平时教学不能满足于已有的解法、单一的解法,要注重对学生数学思维的培养,让学生体验到思考与发现的乐趣.
第一、重视一题多解教学
很多题目,不止一种解法,引导、鼓励学生尝试其他解法,培养学生的发散思维.很多数学新方法、新结论都是由发散思维得到的,数学教学中的一题多解是发散思维的具体体现,教学中加强一题多解的训练,通过综合运用各方面知识解决问题可以开拓学生思路,引导学生更深入地研究问题,培养学生锲而不舍的钻研精神和灵活多变的分析问题和处理问题的能力.
第二、重视多题一解教学
多题一解可使学生从中学会概括、综合、归纳、总结的方法,真正理解具体与抽象、特殊与一般的关系;通过多题一解的训练可以达到强化知识点的目的,收到举一反三的效果.在学生掌握基本知识的基础上,注意多题一解的训练,配合一题多解的练习,能够培养和提高学生分析问题和解决问题的能力.
第三、重视一题多变教学
根据已有题目,适当修改之后,增加变式训练,既能让学生现学现用,检验是否真正掌握,也能提高学生对此类题的本质理解,有效地提高学生的解题能力.
总而言之,充分重视一题多解、多题一解、一题多变的教学,这对于培养学生数学兴趣、数学思维等帮助很大,也有助于学生形成良好的数学认知结构.美国教育心理学家布鲁纳(J.S.Bruner)指出:“获得的知识如果没有完满的结构把它联在一起,那是一种多半会被遗忘的知识.一串不连贯的论据在记忆中仅有短促的可怜的寿命.”一题多解、多题一解、一题多变教学促使学生运用不同知识,寻求不同解法,让零散、孤立的知识与方法,实现一定程度的整合与贯通,让数学学习真正“活”起来.
