舰船自动智能避碰数学模型及其仿真研究
2017-11-03鲍宏杨
鲍宏杨
(南通航运职业技术学院 航海系,江苏 南通 226010)
舰船自动智能避碰数学模型及其仿真研究
鲍宏杨
(南通航运职业技术学院 航海系,江苏 南通 226010)
为了提高舰船航行的安全和效率,达到最佳操船效果,需要建立舰船自动智能避碰数字模型。当前模型在分析舰船避碰风险度的基础上,通过人工智能、进化计算和软计算等方法实现舰船自动智能避碰,存在避碰识别准确率较低的问题。本文提出一种新的舰船自动智能避碰数学模型,首先对舰船会遇态势进行判断;然后建立预测舰船碰撞风险判断模型,预测本舰船实施自动智能避碰方案后的复航时机是否已到,以及本舰船立即复航是否能够让清目标舰船或其他所有目标舰船;最后依据舰船碰撞风险判断结果,以当前舰船潜在碰撞风险为例,建立舰船自动智能避碰数学模型。仿真结果证明,所提模型能够实现舰船自动智能避碰。
舰船;自动;智能避碰;数学模型
文献[8]提出了一种基于人工智能和软计算的舰船自动智能避碰数学模型,该模型在分析舰船避碰风险度的基础上通过人工智能和软计算等方法建立舰船自动智能避碰数学模型,存在避碰识别准确率较低的问题。文献[9]主要综述了模糊神经网络、人工智能系统和免疫算法等在舰船自动智能避碰中的应用,并在此基础上建立了舰船自动智能混合避碰数学模型。该模型存在稳定性较差的问题。文献[10]提出了一种基于拟态物理学算法的舰船自动智能避碰数学模型,首先将《国际海上避碰规则》中的相关条例作为约束性条件限定舰船避碰问题的可行域空间;然后计算舰船最近会遇举例和航行损失的舰船避碰目标函数,通过迭代进化获取舰船避碰全局最优解;最后利用拟态物理学算法建立舰船自动智能避碰数学模型。该模型存在避碰识别准确率较低,反应时间较慢的问题。
为了解决上述模型存在的问题,提高舰船航行的安全系数,提出一种新的舰船自动智能避碰数学模型,并通过仿真实验证明,所提模型能够实现舰船的自动智能准确避障,具有良好的应用价值。
1 舰船自动智能避碰数学模型研究
1.1 舰船会遇态势判断
为了实现舰船自动智能避碰,需要对舰船会遇态势进行判断,为后续判断目标舰船是否存在潜在碰撞风险提供参考依据。具体操作过程如下:
假设Q舰船舷角表示目标舰船相对于本舰船的方位,由0°到180°向右或向左计量。∆C表示目标舰船航向CT与本舰船航向CO之差,即∆C=CT–CO。
根据《国际海上避碰规则》,舰船会遇态势可以分为舰船对遇、舰船交叉相遇和舰船追越3种类型,通常情况下舰船碰撞态势可以分为以下几类:
1)舰船对遇态势:当2艘舰船在相反或接近相反的航向上相遇至有构成碰撞风险的态势,即Q≤5°,且∆C 在 174°~186°之间。
2)舰船的右舷交叉相遇:2艘舰船首向交叉,且目标舰船位于本舰船右舷。根据舰船会遇角度不同还可以分为:
①舰船右舷小角度交叉相遇:Q<45°,且∆C在186°~210°之间;
②舰船右舷大角度交叉相遇:Q<112.5°,且∆C 在 210°~360°之间。
3)舰船的左舷交叉相遇:2艘舰船首向交叉,且目标舰船位于本舰船左舷。根据舰船会遇角度不同还可以分为:
①舰船左舷小角度交叉相遇:Q<45°,且∆C在150°~174°之间;
②舰船左舷大角度交叉相遇:Q<112.5°,且∆C 在 0°~150°之间。
舰船追越态势:1艘舰船从其他舰船正橫后大于22.5°的某一方向赶上其他舰船时,即该舰船对所追越的舰船所处位置,在夜间智能看见被追越舰船的尾灯而无法看到其任意一个舷灯时,被认定是在追越中,即舰船目标 Q>112.5°,且∆C 在 0°~90°或者 270°~360°之间,目标舰船速度Vt大于本舰船速度Vo。
舰船被追越态势:Q<arcsin(0.924×Vt/Vo),且∆C 在 0°~90°或者 270°~360°之间,目标舰船速度 Vt小于本舰船速度Vo。
假设d表示目标舰船相对于本舰船的距离,则本舰船在x,y轴上的速度矢量计算表达式为:

目标舰船在x,y轴上的速度矢量表示为:

本舰船与目标舰船的相对运动速度矢量计算公式如下:
1)在x,y轴上的相对运动速度矢量分别为

2)在x,y轴上的相对速度大小计算表达式为

3)在x,y轴上相对航行的速度为

当VyR<0时,α=180°;当VxR≥0时,分为2种情况,即 VxR>0 时,α=0°;VxR=0 时,α=360°。
目标舰船方位的计算表达式为
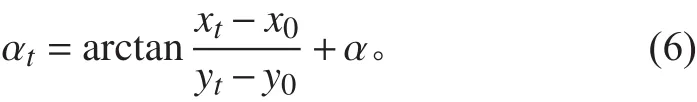
则目标舰船相对方位、目标舰船真方位以及本舰船航行关系的计算公式为

目标舰船与本舰船航向交叉角计算表达式为

根据上述计算结果,可以求出本舰船与目标舰船的转向避碰决策DCPA和复航决策TCPA,其表达式分别如下:
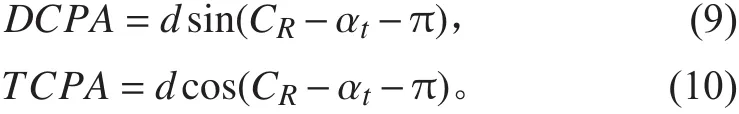
式中:R为风险目标舰船与本舰船的距离。
1.2 预测舰船碰撞风险判断模型
在对舰船会遇态势分析的基础上,建立预测舰船碰撞风险判断模型,预测本舰船实施自动智能避碰方案后的复航时机是否已到,以及本舰船立即复航是否能够让清目标舰船或其他所有目标舰船(多目标舰船会遇情况)。详细描述过程如下:
定义ZXFA代表舰船自动智能避碰执行方案的标识符,取 “0”代表舰船避碰方案形成以及实施前;取 “1”代表舰船避碰方案已经开始实施。
当ZXFA=0时

式中:SDA max[i]表示模糊边界的外边界,是计算舰船碰撞风险避碰幅度的依据;0.725×SDA max表示模糊边界的内边界,是判断舰船潜在碰撞风险的阈值:SDA[i]表示基于当时舰船会遇态势形成避碰方案时,考虑舰船密度等影响因素后各目标舰船和本舰船的实际安全会遇距离。
当ZXFA=1时
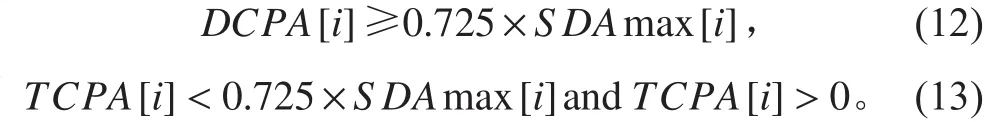
式中:i=1,2,…N,N表示目标舰船总数。SDA[i]的取值取决了舰船自动智能避碰方案安全水平safelevel的取值。
1.3 舰船自动智能避碰数学模型的建立
依据1.2节舰船碰撞风险判断结果,以当前舰船潜在碰撞风险为例,建立舰船自动智能避碰数学模型。
假设WX代表当前风险目标舰船总数标识符;NWX代表预测舰船自动智能避碰方案存在新风险舰船目标总数标识符;WX[i]和NWX[i]分别代表当前目标舰船和预测目标舰船状态标识符,取 “0”代表舰船没有潜在碰撞风险,取 “1”代表舰船有潜在碰撞风险。以当前舰船潜在碰撞风险为例,建立舰船自动智能避碰数学模型,具体步骤如下:
1)假设N=1,满足式(11),且ZXFA=0,或者满足式(12),且ZXFA=1,则判断目标舰船不存在潜在碰撞风险,设定WX[i]=0,转到步骤4;
否则假设满足上述式(13),且ZXFA=0,则判断目标舰船存在潜在碰撞风险,设定WX[i]=1,满足WX=WX+1,转到步骤4;
否则假设满足上述式(13),且ZXFA=1时,则说明目标舰船采取了避碰不协调行动,设定WX[i]=1,转到步骤4;
否则转到步骤2;
2)如果ZXFA=0,且N>1:
假设满足上述式(13),则判定目标舰船存在潜在碰撞风险,设定WX[i]=1,WX=WX+1;
否则,设定WX[i]=0,转下一循环,直到i=N,再转到步骤4;
否则当ZXFA=1时,转到步骤3;

3)假设满足上述式(12)或者满足上述式(13),且TC[i]≥TR、或者满足上述式(13)且满足以下条件:则认定为新进入舰船航行监测区域,存在潜在风险的目标舰船,但是暂时不会构成碰撞威胁,则判定该目标舰船不存在潜在碰撞威胁,设定WX[i]=0;
否则判断该目标舰船存在碰撞风险,则设定WX[i]=1,WX[i]=0,转到下一循环的潜在碰撞风险判断,直到i=N,停止对各个目标舰船潜在碰撞风险的判断,转到步骤4;
4)根据风险舰船累积数量WX总体判断是否存在碰撞风险;
假设WX=0:当ZXFA=0时,则对目标舰船进行分析;而当ZXFA=1时,则恢复舰船航向;
假设WX≠0:当ZXFA=1时,作出舰船自动智能避碰方案;当ZXFA=0时,则对舰船会遇态势进行分析判断、执行舰船自动智能避碰。
至此完成舰船自动智能避碰模型的建立。
2 实验结果与分析
为了更好地开展舰船自动智能避碰模型研究,采取有效的计算机仿真实验进行检验,解决单机仿真实验难以检验目标舰船不协调情况下的自动智能避碰决策效果以及实际舰船试验难度较大等问题,实验引入大连海事大学自主研发的舰船操纵模拟器平台,在此平台基础上,嵌入本文模型的动态链接库,搭建 “舰船安全航行和自动智能避碰计算机仿真测试平台”作为舰船自动智能避碰数学模型的测试设备,利用该平台实现多目标舰船对抗自动智能避碰过程监控的仿真试验。计算机仿真实验平台由控制台PC机、5台本舰船PC机组成,控制台PC机与本舰船PC机间采用无线传感网络联结。实验过程中运用的舰船模型参数设置如表1所示。

表1 舰船模型参数设置Tab. 1 Parameters setting of ship model
2.1 模拟舰船对遇态势的案例
海上天气良好,舰船能见度大于8 nmile,微风(风速为5 kn,风向为000°),本舰船OS的坐标为51°11.726'N 5.014'W,舰船航向为000°,舰船航速为14.8 kn,目标舰船 TG的坐标为 51°15.068'N 10°5.012'W,舰船航向为180°,舰船航速为16.7 kn,2艘舰船之间的距离为3.408 nmile,DCPA为0.152 nmile,TCPA为6.5 min,目标舰船TG与本舰船OS的相对航行速度为20.7 kn,2艘舰船构成对遇态势。根据《国际海上避碰规则》2艘舰船互为避让关系,都需要采取避让行为,当2艘舰船距离为2.78 nmile时,模型计算舰船碰撞风险系数CRI达到0.672,此时,模型开始调用舰船自动智能避碰方案:本舰船OS以右舵6.8°,持续到舰船的ROT到达10.8°/min时,进行回舵,把定操作,此时的舰船改向为9.6°,目标舰船TG以右舵5°,持续到舰船的ROT到达11.7°/min时进行回舵,把定操作,此时的舰船改向为191.6°,模型通过试验以上自动智能避碰方案,实现舰船的成功避让。模型运行过程中的DCPA和CRI变化的历时曲线如图1所示。设CRI的单位为H。
2.2 舰船追越态势仿真试验

图1 DCPA和CRI变化的历时曲线Fig. 1 The diachronic curve of DCPA and CRI
本舰船OS的坐标为51°11.786'N 5.004'W,舰船航向为357°,舰船航速为19.8 kn,目标舰船TG的坐标为 51°12.828'N 10°5.092'W,舰船航向为 000°,舰船航速为7.8 kn,2艘舰船之间的距离为11.2 nmile,DCPA为0.01 nmile,TCPA为5.6 min,目标舰船TG与本舰船OS的相对航行速度为11.7 kn,2艘舰船构成追越态势。本舰船OS为追越舰船,本舰船位于目标舰船右舷并从目标舰船右舷追越目标舰船船首,2艘舰船之间构成碰撞危险,根据《国际海上避碰规则》2艘舰船互为避让关系,本舰船OS采取避让行为,根据计算舰船碰撞风险系数CRI达到0.628,此时,模型开始调用舰船自动智能避碰方案:本舰船OS以本舰船OS以右舵6.8°,持续到舰船的ROT到达14.8°/min时,进行回舵,把定操作,此时的舰船改向为9.8°,目标舰船TG以右舵5°,持续到舰船的ROT到达11.7°/min时进行回舵,把定操作,此时的舰船改向为191.6°,模型通过试验以上自动智能避碰方案,实现舰船的成功避让。模型运行过程中DCPA和CRI变化的历时曲线如图2所示。
2.3 舰船交叉态势仿真实验

图2 DCPA和CRI变化的历时曲线Fig. 2 The diachronic curve of DCPA and CRI
本舰船OS的坐标为51°11.786'N 5.004'W,舰船航向为357°,舰船航速为12.3 kn,目标舰船TG的坐标为 51°12.502'N 10°2.892'W,舰船航向为 300°,舰船航速为14.8 kn,2艘舰船之间的距离为1.586 nmile,DCPA为0.173 nmile,TCPA为7.06 min,目标舰船TG与本舰船OS的相对航行速度为12.7 kn,目标舰船TG位于本舰船真方位右舷62.2°,2艘舰船构成交叉态势,2艘舰船之间构成碰撞危险,根据《国际海上避碰规则》目标舰船TG保持航向和航速,本舰船OS需要采取避让行为,本舰船向右转向,过目标舰船船尾。计算舰船碰撞风险系数CRI达到0.64,此时,模型开始调用舰船自动智能避碰方案:本舰船OS以本舰船OS以右舵14.8°,持续到舰船的ROT到达20.8°/min时,进行回舵,把定操作,此时的舰船改向为24°,模型通过试验以上自动智能避碰方案,实现舰船的成功避让。模型运行过程中DCPA和CRI变化的历时曲线如图3所示。
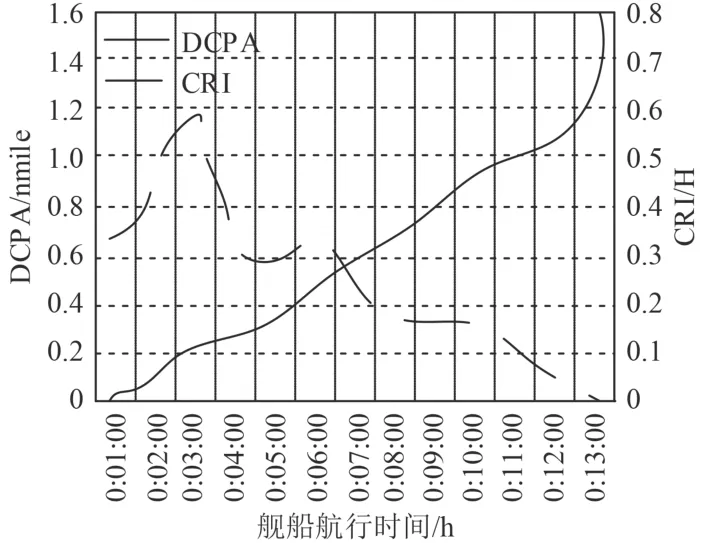
图3 DCPA和CRI变化的历时曲线Fig. 3 The diachronic curve of DCPA and CRI
2.4 多舰船会遇态势仿真实验
本舰船OS的坐标为51°11.676'N 5.003'W,舰船航向为000°,舰船航速为16.2 kn,目标舰船TG的坐标为51°13.402'N3.792'W,舰船航向为213°,舰船航速为14.5 kn,与本舰船OS距离13.937 nmile,本舰船真方位右舷23.6°,DCPA为0.248 nmile,TCPA为3.936 nmile,目标舰船TG2位于51°13.392'N10°6.292'W,目标舰船的航向为150°,航速为14.2 kn,与本舰船OS之间的距离为1.948 nmile,目标舰船真方位左舷335.2°,DCPA为0.369 nmile,TCPA为3.878 min。本舰船OS与目标舰船TG1和目标舰船TG2均构成交叉碰撞危险。本舰船OS与目标舰船TG1和目标舰船TG2分别采取右让和左让的自动智能避碰决策。由此可知,本舰船OS智能采取保持航向,降低航速;目标舰船TG1和目标舰船TG2则分别采取左让和右转避让决策。此时,模型开始调用舰船自动智能避碰方案:本船车钟由Full Ahead(100.3 rpm)对应舰船航速16.2 kn降至Slow Ahead(70.2 rpm)对应航速12.3 kn,目标舰TG1向左转向30°,其航向调整为185°(避碰模型建议:左舵16°,持续到ROT到达23°/min时,进行回舵,把定操作,此时目标舰船TG1改向为185°);目标舰船TG2向右转向25°,航向方向调整为175°(避碰模型建议:右舵13°,持续到ROT到达28.9°/min时,进行回舵,把定操作,此时目标舰船TG1改向为175°)。模型通过试验以上自动智能避碰方案,实现舰船的成功避让。模型运行过程中DCPA和CRI变化的历时曲线如图4所示。

图4 DCPA和CRI变化的历时曲线Fig. 4 The diachronic curve of DCPA and CRI
3 结 语
采用当前模型对舰船自动智能避碰对潜在碰撞风险分析的不全面,使得避碰决策执行不协调,为此提出一种新的船舶自动智能避碰数学模型,并通过计算机仿真实验对船舶自动智能避碰数学模型进行检验,证明了所提模型的有效性。对航海的自动化技术提供了可靠保证。
[1]陈姚节, 李爽, 范桓, 等. 基于速度矢量坐标系的多船自动避碰研究[J]. 计算机仿真, 2015, 32(6): 420–424.
CHEN Yao-jie, LI Shuang, FAN Huan, et al. Automatic collision avoidance of multi-ships based on velocity vector coordinate[J]. Computer Simulation, 2015, 32(6): 420–424.
[2]管小清, 常青, 梁冠豪, 等. 一种冗余机械臂的多运动障碍物避障算法[J]. 计算机测量与控制, 2015, 23(8): 2802–2805.
GUAN Xiao-qing, CHANG Qing, LIANG Guan-hao, et al.Multiple mobile obstacles avoidance algorithm for redundant manipulator[J]. Computer Measurement & Control, 2015,23(8): 2802–2805.
[3]尹新城, 胡勇, 牛会敏. 未知环境中机器人避障路径规划研究[J]. 科学技术与工程, 2016, 16(33): 221–226.
YIN Xin-cheng, HU Yong, NIU Hui-min. Path planning study for robot obstacle avoidance in unknown environment[J].Science Technology and Engineering, 2016, 16(33): 221–226.
[4]周恺. 信息素模糊逻辑导引的机器人室内避障算法[J]. 科技通报, 2015, 31(12): 220–222.
ZHOU Kai. Indoor robot obstacle avoidance algorithm introduction of pheromone fuzzy logic guidance[J]. Bulletin of Science and Technology, 2015, 31(12): 220–222.
[5]刘彦戎. 基于STC89C51RC单片机的智能遥感避障小车的系统设计[J]. 电子设计工程, 2017, 25(3): 45–48.
LIU Yan-rong. Design of intelligent obstacle avoidance car remote sensing system based on STC89C51RC microcontroller[J]. Electronic Design Engineering, 2017, 25(3): 45–48.
[6]曹海. 人工免疫算法的船舶避碰智能策略研究[J]. 舰船科学技术, 2016, 38(2): 10–12.
CAO Hai. Research on intelligent strategy of ship collision avoidance of artificial immune algorithm[J]. Ship Science and Technology, 2016, 38(2): 10–12.
[7]贺益雄, 黄立文, 牟军敏, 等. 交叉相遇局面让路船自动避碰行动方案[J]. 哈尔滨工程大学学报, 2015(8): 1024–1029.
HE Yi-xiong, HUANG Li-wen, MOU Jun-min, et al. A scheme for automatic collision avoidance of a give-way vessel in the crossing situation[J]. Journal of Harbin Engineering University, 2015(8): 1024–1029.
[8]熊勇, 贺益雄, 黄立文. 基于速度障碍的多船自动避碰控制方法[J]. 中国航海, 2015, 38(3): 46–51.
XIONG Yong, HE Yi-xiong, HUANG Li-wen. Multi-ship collision avoiding control considering velocity obstacle[J].Navigation of China, 2015, 38(3): 46–51.
[9]吕红光, 尹勇, 尹建川. 混合智能系统在船舶自动避碰决策中的应用[J]. 大连海事大学学报, 2015, 41(4): 29–36.
LV Hong-guang, YIN Yong, YIN Jian-chuan. Application of hybrid intelligent systems in automatic collision avoidance decision-making for ships[J]. Journal of Dalian Maritime University, 2015, 41(4): 29–36.
[10]吴蓓. 船舶避碰中灰色数据挖掘研究[J]. 舰船科学技术,2016, 38(9A): 151–153.
WU Bei. The research of gray data mining algorithm in the ship collision avoidance system [J]. Ship Science and Technology, 2016, 38(9A): 151–153.
Research on automatic mathematical model of ship's automatic intelligent collision and its computer simulation
BAO Hong-yang
(Department of Navigation, Nantong Vocational and Technical Shipping College, Nantong 226010, China)
In order to improve the safety and efficiency of ship navigation, to achieve the best boat effect, the need for ship automatic intelligent collision avoidance digital model to study. Based on the analysis of the risk of collision avoidance,the current model can realize the automatic collision avoidance of ships by means of artificial intelligence, evolutionary computation and soft computing. There is a problem that the accuracy of collision avoidance is low. In this paper, a new mathematical model of automatic collision avoidance of ships is proposed. First, the situation of ship encounters is judged. Then, the ship collision risk judgment model is established to predict the recovery of the ship after the automatic intelligent collision avoidance whether the ship has arrived, and whether the ship can be re-deployed immediately to clear the target ship or all other target ships. Finally, according to the ship collision risk judgment results, the current ship potential collision risk, for example, the establishment of ship automatic intelligence collision mathematical model. Computer simulation experiments show that the proposed model can achieve the ship automatic intelligent collision avoidance.
ship;automatic;intelligent collision avoidance;mathematical model
U675
A
1672 – 7649(2017)10 – 0164 – 06
10.3404/j.issn.1672 – 7649.2017.010.033
0 引 言
随着现代科技的不断发展和进步,特别是计算机技术、传感器技术、人工智能技术以及模糊数学理论的发展,航海技术发生了重大变革[1–2]。世界航运经济得到迅猛发展,舰船总量的日趋增加,舰船航行速度的不断提升是舰船安全航行面临的巨大挑战,同时也对舰船航行的自动化和智能化发展起到了推动性作用[3–4]。相比较早期舰船航行的导航系统功能较为单一,现代化舰船装备精良,但是在舰船航行过程中,舰船之间的碰撞、舰船搁浅、舰船触礁等海洋事故仍旧频发。这些频频发生的海洋事故除了造成大量人员伤亡之外还造成现代海洋生态系统破坏[5]。通过分析这些海洋事故发生的数据可知,除了一些外在不可抗力引发的海洋事故之外,舰船碰撞事故发生的概率还在持续增长[6]。据可靠数据统计,96%以上的舰船碰撞海洋事故是由于舰船值班驾驶员没能严格遵守《国际海上避碰规则》导致的。为了提高舰船航行的安全和效率,达到最佳操船效果,需要对舰船自动智能避碰数字模型进行研究。当前的舰船自动智能避碰数学模型主要将可拓学与避碰学相结合[7],实现舰船自动智能避碰,存在实际应用性能较差的问题。
2017 – 06 – 14
鲍宏杨(1979 – ),男,硕士,讲师,研究方向为船舶避碰与导航、航海职业教育。
