异步电动机矢量控制变频调速系统的建模与仿真研究

王 宏

(辽宁电力勘测设计院 新能源部，辽宁 沈阳 110179)

异步电动机矢量控制变频调速系统的建模与仿真研究

王 宏

(辽宁电力勘测设计院 新能源部，辽宁 沈阳 110179)

矢量控制技术是借鉴直流电机的转矩关系，通过坐标变换的方法，得到与直流电机转矩形式相似的异步电机解耦转矩表达式。仿真是对其进行研究的一个重要的不可缺少的手段。异步电机矢量控制变频调速采用PWM 逆变器为其提供驱动电能，整套系统采用结构化和模块化的方法通过Simulink和Power System Blocksets来对异步电机变频调速系统进行数学建模和仿真模拟化，简化了操作过程，最终验证了建模方法的有效性。

异步电动机；变频调速；坐标变换；矢量控制

现代交流调速系统的快速发展使得交流电机在交流调速领域里有了新的突破，通过定向转子磁场、变换矢量从而提升电机效率，由于自动控制的复杂不确定因素，需要控制系统达到所需控制要求。针对异步电机矢量控制变频调速系统进行建模和仿真，简化交流电动机转速和磁链控制系统操作过程。

1 矢量控制的基本方程式及系统结构

通过相同的旋转磁动势为依据，在静止三相坐标系统里，定子交流电流通过静止三相坐标将等同于旋转坐标系操控异步电动机直流电流，来完成磁通及其转矩的控制，从而使直流电机能够正常运转。为使模型的建立更加简洁、明了，根据异步电动机在两相同步旋转坐标系下的数学模型，充分利用MATLAB强大的矩阵运算功能及Simulink提供的S函数模块构建了普通异步电动机的仿真模型，并对实际电机进行了仿真。

异步电动机数学模型分别如下，其中包括电压、磁链和转矩方程:

(1)

(2)

Te=np*Lm(isq*ird-isd*irq)

(3)

当两相同步旋转坐标系按转子磁链定向时,应有φrd=φr,φrq=0即得:

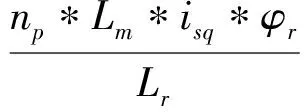
(4)

(5)

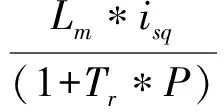
(6)

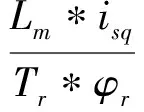
(7)

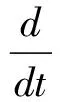
图1 矢量控制变频调速系统结构

2 变频调速数学建模

变频调速在变换前后总功率不变的条件下,三相/两相变换数学模型如下：

(8)

旋转变换数学模型为

(9)

转子磁链观测器数学模型为

(10)

转差角频率

(11)

转子磁链相位角

(12)

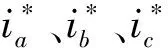
3 仿真结果

三相静止坐标系到两相任意旋转坐标系的变换及其反变换已经建立在power system模型库中，提取路径为power system blockset/extra library/measurements/abc_to_dq0 transformation(dq0_to_abc transformation)。矢量变换的仿真如下：建立的观察三相电压3s/2s和3s/2r变换的仿真模型如图3所示。图中调用了两个abc_to_dq0 transformation模块，调用的abc_to_dq0模块有两个输入端和一个输出端。输入端abc连接需变换的三相信号，sin_cos输入端为d-q坐标系d轴和静止坐标系的A轴之间夹角的正、余旋信号，输出端dq0输出变换后的d轴和q轴分量以0轴分量。在模型中三相电压信号有可编程信号源(3-phase programmable source)产生，夹角由时钟(clock)、常数(constant)模块产生θ=wt=2πft,并经sin、cos模块产生正、余旋信号。

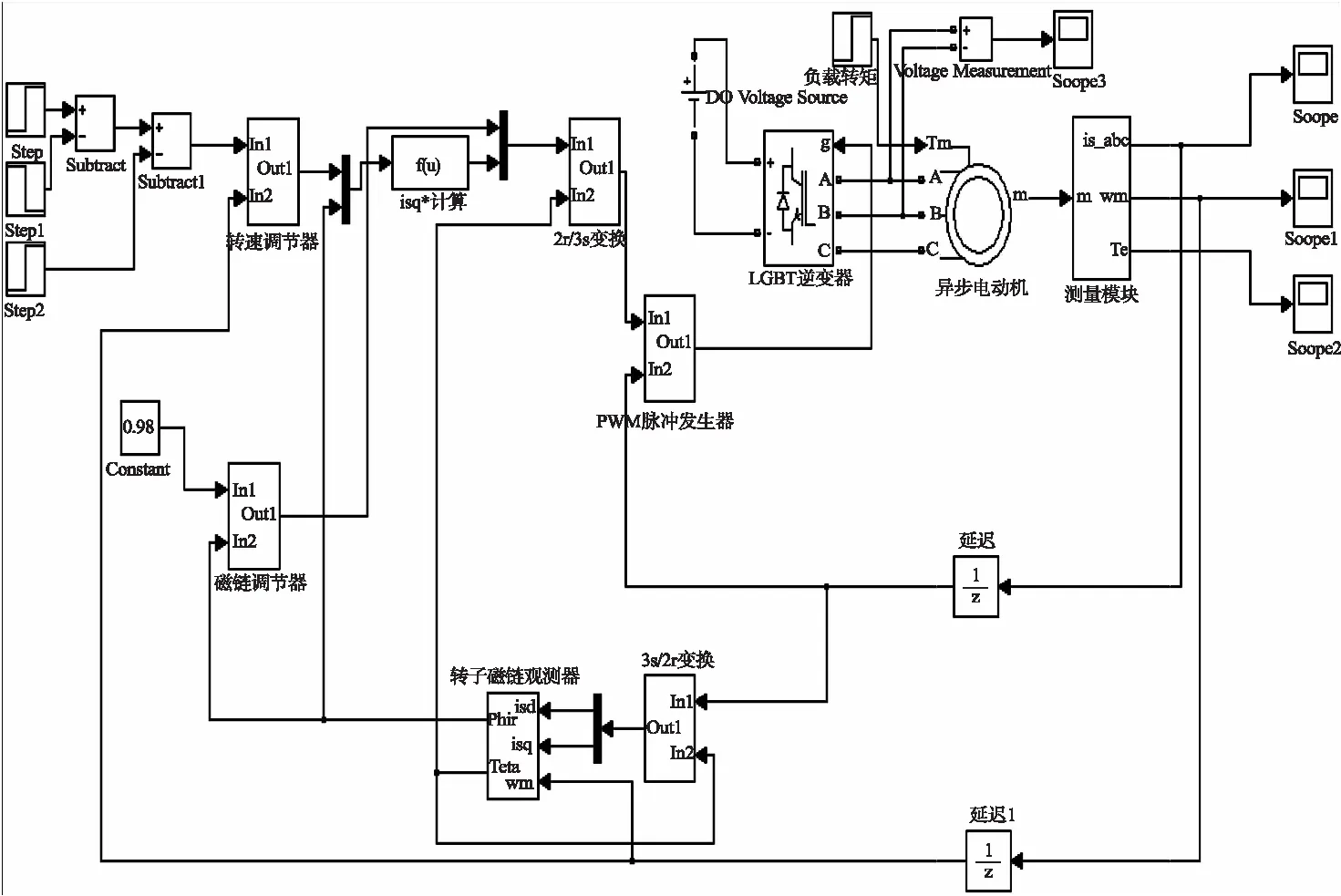
图2 矢量控制变频调速系统仿真模型

图2中的两个abc_to_dq0模块，一个用于3s/2s变换，另一个用于3s/2r变换。用于3s/2s变换时，设置常数模块值为零，即θ=wt=0，这意味着d-q坐标系已蜕化为静止的α-β坐标系，abc_to_dq0模块现在实现的是3s/2s变换。用于3s/2r变换时，设置常数模块值为314，即w=2π×50 Hz。

仿真结果如图3所示，其中图a为变换前的三相电压；图b为经3s/2s变换后静止二相坐标系上的电压波形，这二相电压互差90°；图c为经过3s/2r变换后旋转二相坐标系上的电压波形，由于所选角频率w=2πf，与电源角频率同步，所以在二相同步旋转坐标系上的电压已经是直流。

对异步电动机的矢量控制进行MATLAB建模,其参数值Pm=5.6 kW；f=60 Hz；VL=380 V；Rs=0.098 Ω；Rr=0.332 Ω；

图4至图7分别为定子线电压、线电流、电磁转矩和速度上升波形。

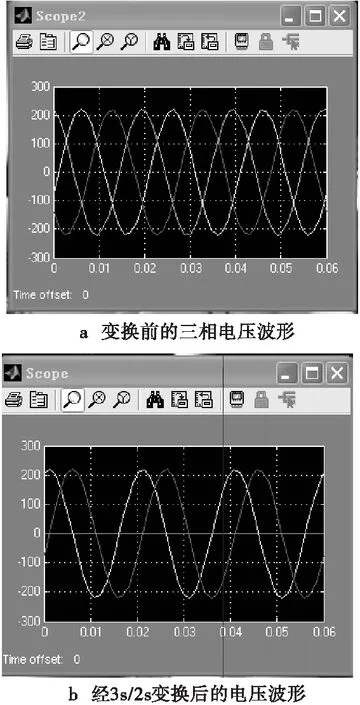
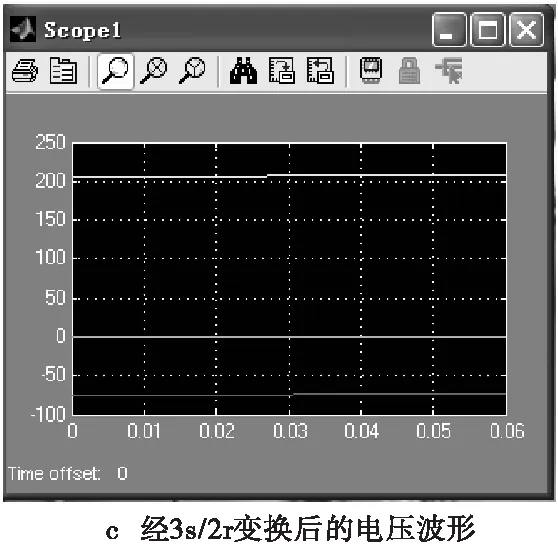
图3 电压变换波形

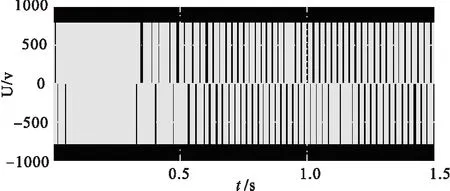
图4 定子线电压波形

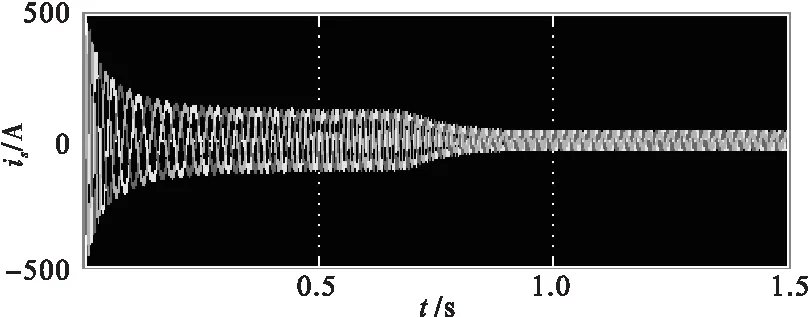
图5 定子线电流波形

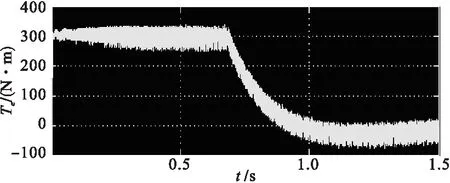
图6 电磁转矩波形

图7 速度上升波形

4 结 论

设定调节器转矩极限300 N·m，仿真结果可以看出系统在接到指令启动瞬间，峰值电流为500 A,恒转矩阶段转矩始终保持在设定的极限值范围内，0.8 s时刻转子角速度达到最大，此时速度为130 rad/s。

利用矢量控制实现对异步电动机的控制。其中通过坐标变换实现了对异步电动机的矢量控制，主要是根据三相静止坐标系和两相静止坐标系的变换及两相静止坐标系到两相旋转坐标系的变换建立起三相静止坐标系到两相旋转坐标系的关系，从中导出函数关系式，进而对异步电动机的矢量控制进行MATLAB建模，进一步证明了异步电动机的非线性、强耦合等特点。

[1] 李文静,熊光煜.基于MATLAB的异步电动机矢量控制变频调速系统的仿真[J].电力学报,2006,17(9):146-153.

[2] 张兴华.基于Simulink/PSB的异步电机变频调速系统的建模与仿真[J].系统仿真学报,2005,21(2):2099-2103.

[3] 王宏宇,胡 丹,车 畅.异步电动机矢量控制系统Simulink仿真[J].四川工业学院学报,2004,23(3):66- 68.

[4] 王 敏.控制系统原理与MATLAB仿真实现[M].北京:电子工业出版社,2014.

[5] 李 忱，陈 万，尚志建.基于自适应法的永磁调速器的混沌反控制研究[J].沈阳工程学院学报：自然科学版,2017,13(2):137-142.

[6] 陈伯时.电力拖动自动控制系统—运动控制系统[M].北京:机械工业出版社,2015.

[7] 吴晓燕,张双选.MATLAB在自动控制中的应用[M].西安:西安电子科技大学出版社,2006.

[8] 余名俊,李 岚,王秀丽.异步电动机的MATLAB建模与仿真[J].电力学报,2006,35(3):35-37.

[9] Darryl Morrell.Design of an introductory MATLAB course for freshman engineering students[J].American Society for Engineering Education,2007：341-346.

[10] Ganapathy Narayanan.Teaching of essential MATLAB commands in applied mathematics course for engineering technology[J].American Society for Engineering Education,2007：3055-3068.

ModelingandSimulationofVectorControlVariable-FrequencySpeedControlSystemofAsynchronousMotor

WANGHong

(NewEnergyDepartment,LiaoningElectricPower&SurveyDesignInstituteCo.,Ltd.,Shenyang110179,LiaoningProvince)

Vector control technology makes use of the DC motor's torque relationship to get an expression of torque for asynchronous motor through the coordinate transposition. The Simulink and Power System Blocksets utilized on variable-frequency drive of asynchronous motors by modeling and simulating is proposed. A structure and blocking modeling method is applied to set up the model of vector control drive for anasynchronous motor. And the function of every sub-model is introduced in detail. The actualsystem was simulated by the proposed model. It could be modified conveniently and obtained easily. The simulation results verified the effectiveness of the proposed modeling method.

Asynchronous motor;Variable-frequency drive;Coordinate transformation;Vector control

A

1673-1603(2017)04-0353-04

(责任编辑魏静敏校对张凯)

2017-02-25

王 宏(1964-)，女，辽宁沈阳人，高级工程师。

10.13888/j.cnki.jsie(ns).2017.04.011