基于LS-DYNA的爆炸流场荷载的数值模拟研究*

储 程，赵跃堂，胡 康

(1.解放军理工大学 国防工程学院，江苏 南京 210007；2.爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007)

基于LS-DYNA的爆炸流场荷载的数值模拟研究*

储 程1,2，赵跃堂1,2，胡 康1,2

(1.解放军理工大学 国防工程学院，江苏 南京 210007；2.爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007)

随着微型计算机计算能力的提高以及数值方法和商业软件的推动，基于有限元方法的数值模拟在科学和工程研究中得到广泛应用，一些复杂的物理问题可以容易地进行数值模拟研究。介绍了在微型机上基于LS-DYNA软件分别使用普通ALE方法和ALE映射方法模拟限制空间内爆炸波流场荷载的方法，并对结果进行了比较分析。研究表明，爆炸波传播及荷载可以在微型机上进行有效模拟；ALE网格映射方法对于普通ALE方法是一种改进，可以降低结果对网格的敏感性。

微型机；数值模拟；爆炸波；任意拉格拉日欧拉方法

0 引言

微型计算机计算能力的提升和数值计算方法的发展，为研究科学技术中的复杂问题提供了新的研究方法，即数值模拟方法。数值模拟方法通过对复杂的数学物理问题进行建模，最终简化为可数值求解的微分方程(组)，通过其强大的数值求解算法，最终将计算结果直观清晰地展现给科研工作者，因而在各类科学和工程问题研究中得到了广泛的应用[1-3]。

爆炸波的传播及其荷载是爆炸力学中最重要的科学问题。由于爆炸试验本身具有一定的危险性和不可控性，且限制空间内爆炸后空气爆炸波流场十分复杂，测量困难，因此计算机数值仿真成为此类学科理论研究和实验研究之外并行的一种研究方法，日益受到重视[4-5]。目前在爆炸力学方面广泛使用的有限元软件主要有ANSYS、LS-DYNA、ABAQUS和AUTODYNA等[6]，这些有限元软件都可以在微型计算机上运行，其中LS-DYNA是显示非线性动力分析通用有限元程序，对爆炸的模拟提供了良好的支持，但由于爆炸模拟本身的复杂性，很多因素可能影响模拟结果的可靠性，例如材料的状态方程、本构模型的参数、网格划分精细度、计算控制参数设置[7]等。本文介绍限制空间内点源爆炸所造成的空气爆炸波流场及其荷载，对比两种不同方法的结果，通过对比分析得出比较可靠的模拟方法。本文研究基于LS-DYNA软件进行。

1 ALE方法

通常而言，动力学问题的数值模拟过程中将涉及三种算法：Lagrangian算法、Euler算法和任意拉格朗日-欧拉(Arbitrary Lagrangian Eulerian,ALE)算法。与之相对应，模型划分的网格分别称为Lagrangian网格、Euler网格和ALE网格。在Lagrangian算法中，网格节点将允许和材料节点共同运动和变形，这种算法较适合于固体材料的模拟，其缺点在于无法模拟大变形的情况，网格的畸变将造成计算的终止或出错。在Euler算法中，网格节点的空间位置是固定不变的，并不随着材料节点一同运动和变形，可以克服大变形带来的无法模拟计算的问题，对于流体材料方面的模拟效果较好。ALE算法则结合了Lagrangian算法和Euler算法各自的特点，对于固体材料将采用Lagrangian算法，允许节点与材料共同运动与变形，而流体材料则采用Euler算法，网格节点固定不变，采用ALE算法既准确地描述固体的响应特征也解决了大变形畸变带来的计算问题[6,8]。

ALE适合用来模拟爆炸波流场这种大变形运动，缺点是不能用于大尺度建模，因为每个单元须很小以捕捉爆炸压力，而如果网格很细则导致单元数量庞大，对于微型机来说可能导致计算时间过长。为此LS-DYNA又提供了一种ALE网格映射方法。映射(MAPPING)技术，首先可以提高运算效率，其次由于用映射技术可以实现从1D(即一维)到2D、1D到3D、2D到2D、2D到3D、3D到3D和3D到2D的映射，因而可以在被映射模型中使用较粗糙的网格，从而可以进行大尺度建模[37]。目前关于这两种方法对计算结果的影响的研究还很少。

2 材料模型和参数

空气和炸药分别可用关键字*MAT_NULL以及关键字*MAT_HIGH_ EXPLOSIVE_BURN来模拟，其参数设置分别如表1和表2所示。空气和炸药的状态方程分别用关键字*EOS_LINEAR_POLYNOMAL和*EOS_JWL来模拟，其参数设置分别如表3和表4所示。

表1 空气材料模型参数(单位：kg，m，s，Pa)

表2 炸药材料模型参数(单位：kg，m，s，Pa)

表3 空气状态方程参数(单位：kg，m，s，Pa)

表4 炸药状态方程参数(单位：kg，m，s，Pa)

普通的ALE方法直接在空气网格中填充一部分炸药的材料单元，因此炸药与空气网格共用节点；采用ALE映射方法分两步计算，第一步为初始起爆阶段的模拟，采用一维模型，ALE1D算法，炸药处理、材料参数以及状态方程的设定均与上相同，最后通过命令“map=文件名”将计算最后一次循环结束后的信息存入二进制文件中，用于第二步的计算。

第二步采用三维整体模型，只需要建立空气网格模型，无需再定义炸药的网格，引用关键字*INITIAL_ALE_MAPPING并设置好炸药的位置来实现由1D到3D的映射，通过命令“map=文件名”将第一步结束时的信息导入第二步的初始时刻。

3 计算结果对比分析

按照前面介绍的方法，本文对于柱状限制空间中偏心点源爆炸的爆炸波流场分别采用普通ALE方法和ALE映射方法进行了计算，如图 1所示，分别按照爆心环面、爆源近端轴向和远端轴向三类对结果进行对比分析。

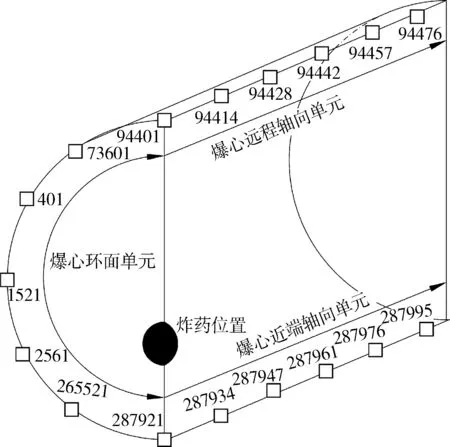
图1 对比爆炸荷载的单元位置

3.1 爆源截面荷载对比

图2为爆源环面内壁单元上反射超压曲线对比，两种方法结果基本一致，但是到了距离爆源最远的单元94401，压力曲线略有不同。

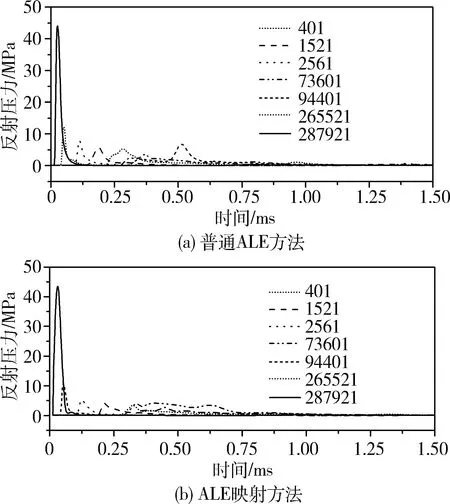
图2 爆心截面反射超压对比

压力曲线的时间积分，即比冲量对比如图3所示，可看出采用ALE映射方法时距离爆源最远的单元94401的比冲量超过距爆源最近的单元287921，而采用普通ALE方法则得出相反结论。

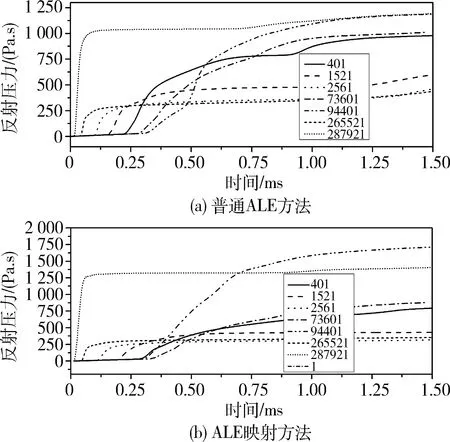
图3 爆心截面反射比冲量对比

3.2 爆源近端轴向的荷载对比

图4对比了采用两种方法分别计算时沿爆源近端轴向上一系列单元的压力。

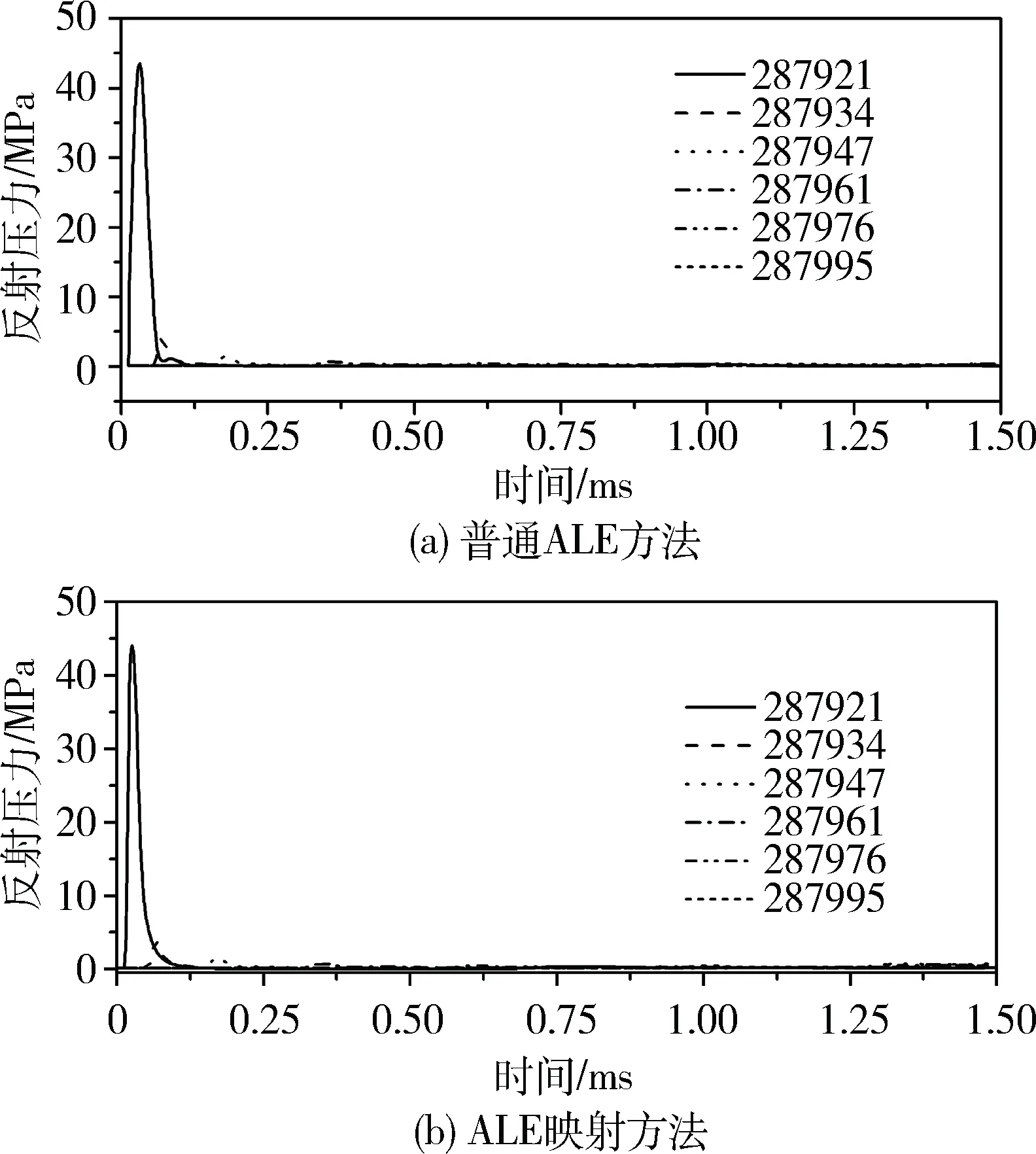
图4 爆源近端轴向单元反射超压对比

图5进一步比较了冲量的对比，可以看出除了个别观测单元(287947)以外，其余单元上的比冲量按照两种方法计算结果接近。

3.3 爆心远端轴向的荷载对比

图6为爆心远端轴向上若干单元的压力曲线对比。采用普通ALE建模算法得出的压力幅值大于ALE映射方法的结果，且94401单元压力波形特征不同。

图7进一步对冲量进行对比，可以看出用ALE映射方法计算时爆源远端轴向第一个单元94401要明显大于轴向上其他单元，而按照普通ALE方法计算出的结果则是前几个单元的结果比较接近。

4 结论

从爆炸流场的时间变化上看，采用普通ALE方法模拟和ALE映射方法结果近似，都能够较好地模拟爆炸波的传播及其与限制边界的相互作用，但这只是定性的结果；定量比较中显示出两种方法计算结果有明显差异，主要表现在以下几个方面：采用ALE映射方法的结果中爆源近端轴向上单元的压力差别不大，仅个别单元冲量有微小差别；两种方法的计算结果中爆源远端轴向上单元的压力差别较大。考虑到ALE普通方法受网格影响较大，因此这种差别主要是来自于网格的影响。相比之下，ALE映射方法的精度更高，计算效率也更高，但是映射过程略复杂，不如普通ALE方法直观和建模方便。综合分析，得出以下基本结论：

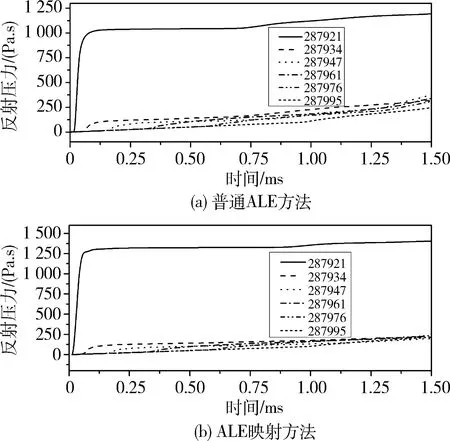
图5 爆源近端轴向单元反射超压对比

图6 爆源远端观测单元的压力曲线对比

图7 爆源远端观测单元的比冲量曲线对比

(1)采用ALE方法，借助有限元软件，即可以在微型计算机上很好地模拟爆炸波及其流场的复杂过程；

(2)在爆炸波荷载的模拟方面，ALE映射方法精度较之普通ALE方法要高，但映射过程易出错，建模不直观；

(3)ALE普通方法精度受限于网格精度，精度太高又容易超出微型计算机的计算能力，因此不适合大尺度建模；但其建模相对直观，因此在小尺度问题中可以采用精细网格并直接采用普通ALE方法进行模拟。

[1] 郭玉琴. 板料冲压仿真技术及其发展[J]. 微型机与应用, 2007,26(1): 73-73.

[2] 胡涛, 狄帮让, 魏建新. 并行高速采样在地震物理模拟采集中的应用[J]. 微型机与应用, 2016,35(4): 101-103.

[3] 李红雷, 李莉华, 贺林,等. 沪崇苏电缆通道热场的研究[J]. 上海电力, 2017(1): 11-14.

[4] 曹玉忠, 卢泽生, 管怀安,等. 抗爆容器内爆炸流场数值模拟[J]. 高压物理学报, 2001,15(2): 127-133.

[5] 彭金华, 汤明钧. 非理想爆源产生的爆炸场数值模拟[J]. 爆炸与冲击, 1991(4): 289-296.

[6] CHENG D S, HUNG C W, PI S J. Numerical simulation of near-field explosion[J]. Journal of Applied Science and Engineering, 2013,16(1): 61-67.

[7] Han Yuzhen, Liu Huabei. Finite element simulation of medium-range blast loading using LS-DYNA[J]. Shock and Vibration, 2015: 1-9.

[8] 张奇, 张若京. ALE方法在爆炸数值模拟中的应用[J]. 力学季刊, 2005,26(4): 639-642.

Numerical simulation of explosion in a confined space using ALE method

Chu Cheng1,2, Zhao Yuetang1,2, Hu Kang1,2

(1. National of Defense Engineering Institute, PLA University of Science and Technology, Nanjing 210007, China;2. State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, Nanjing 210007, China)

With increase of personal computer’s computational capability, together with the development of numerical method, some complicated physical problems can be simulated with microcomputer. In this paper numerical simulation of explosion in a confined space using ALE method on microcomputer was introduced, then two ways of simulation of the blast wave fields in LS-DYNA code were used and the results were compared and analyzed. This study showed that blast wave propagation and the fluid field can be simulated effectively on microcomputer, however, the mesh size has evident influence on the results. ALE Mapping is an improvement to original ALE method.

microcomputer; numerical simulation; blast wave; arbitrary Lagrangian Eulerian method

O383+.1

A

10.19358/j.issn.1674- 7720.2017.20.030

储程，赵跃堂，胡康.基于LS-DYNA的爆炸流场荷载的数值模拟研究[J].微型机与应用，2017,36(20)：108-110,104.

国家自然科学基金项目(51478469)

2017-03-27)

储程(1986-)，通信作者，男，博士研究生，主要研究方向：结构及防护工程。E-mail：iamcci@163.com。

赵跃堂(1967-)，男，博士，教授，主要研究方向：防护工程及防灾减灾工程。

胡康(1993-)，男，硕士研究生，主要研究方向：结构及防护工程。