改进变步长LMS自适应预失真算法研究*

汪琳娜，刘 玲，杨 新

(1.四川工商学院 电子信息工程学院，四川 成都 611745； 2.四川工商学院 云计算与智能信息处理重点实验室，四川 成都 611745)

改进变步长LMS自适应预失真算法研究*

汪琳娜1，刘 玲1，杨 新2

(1.四川工商学院 电子信息工程学院，四川 成都 611745； 2.四川工商学院 云计算与智能信息处理重点实验室，四川 成都 611745)

在数字预失真过程中，针对传统的最小均方差(LMS)自适应算法收敛速度较慢和稳态误差较大的缺点，通过分析各种改进的变步长LMS算法的优势和劣势，提出了一种组合曲线的归一化变步长LMS数字预失真算法。仿真结果表明，新算法在保证预失真效果的前提下，算法性能得到极大提升。

预失真；最小均方差；变步长；归一化

0 引言

面对移动用户数量和带宽需求的快速增长，当采用如最小频移键控(Minimum Shift Keying，MSK)、正交振幅调制(Quadrature Amplitude Modulation,QAM)、正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)等非恒定包络的幅度调制方式提高频谱利用率时，功率放大器(Power Amplifiers, PAs)成为无线通信系统中不可或缺的关键部件，但是其饱和工作带来的非线性(Nonlinearities)失真和记忆效应(Memory effects)使功率放大器的行为建模变得异常困难。数字预失真技术(Digital Pre-Distortion, DPD)是构造一个与功率放大器行为模型相反的预失真器，通过预失真器对输入信号进行预失真，使得系统在不失真的情况下实现线性放大。如何针对记忆非线性对功率放大器进行精确建模以及数字预失真线性化成为当前移动通信研究领域的热点方向之一。基于意大利数学家VOLTERRA V于1887年提出的Volterra 级数，先后出现了一系列记忆功率放大器模型，如Wiener模型[1]、Hammerstein模型[2]、并行Wiener模型[3]、并行Hammerstein模型[4]、Wiener-Hammerstein模型[5]、MP(Memory Polynomial)模型[6]、GMP(Generalized Memory Polynomial )[7]模型、DDR- Volterra (Dynamic Deviation Reduction-based Volterra)[8]模型等，但这些模型在参数辨识方面存在诸多困难。

在基于Voltera级数的数字预失真行为模型中，目前常用的参数辨识方法有自适应算法包括最小均方(Least Mean Square，LMS)算法、递归最小二乘算法(Recursive Least Square Method，RLS)、离散牛顿法(Discrete Newton Method)等。为了更有效地描述带有记忆的非线性系统特性，必须保留较多的模型参数，造成参数实时辨识的难度。因此为降低参数实时辨识的难度，一方面可以通过简化模型减少辨识参数数量，另一方面可以对自适应参数辨识算法进行改进。基于维纳滤波理论的LMS算法虽然其结构简单，计算复杂度低，但是其收敛速度较慢，严重影响了参数辨识的效率。目前国内外已经提出了很多基于改进LMS的自适应算法，如改变LMS步长算法、改变LMS阶数、稀疏LMS算法、带泄露因子的LMS算法、变换域LMS算法、放射投影LMS算法等[6-7,9-11]。本文主要基于变步长的思想提出了一种新的LMS自适应参数辨识算法，仿真结果表明，在保证预失真精度的情况下，基于MP模型采用改进的LMS算法使收敛速度得到明显提升。

1 基于Volterra级数的MP模型

Volterra级数模型是一种重要的有记忆非线性系统模型，其离散P阶截短Volterra级数模型为[12]：

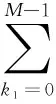
(1)

其中x(n)和y(n)表示系统输入和输出信号的复包络，P为非线性阶数,M为记忆深度,hp(k1,…,kp)为P阶Volterra核函数。把Volterra级数中模型参数看作是由P维空间的延迟k1,k2，…，kp形成的P维超几何体上的点，当延时k1=k2=…=kp时，hn(k1,…，kn)≠0，即去掉Volterra级数中不同延时的交叉项，只保留对角核，而且由于偶阶项产生的直流分量和谐波分量都落在通带以外，因此只保留奇阶项，Volterra级数模型简化为MP模型[6]，其表示为：

(2)

其中K和M分别为MP模型的阶数和记忆深度，akm为MP模型的复系数，|x(n-m)|表示输入复信号x(n-m)的模。

2 自适应预失真结构

设计自适应数字预失真系统包括直接学习结构和间接学习结构。由于直接学习结构需要提前获得功率放大器的模型参数，实现复杂且计算量大，很多优化辨识参数的算法难以直接应用，因此本文主要采用间接学习结构,如图1所示。

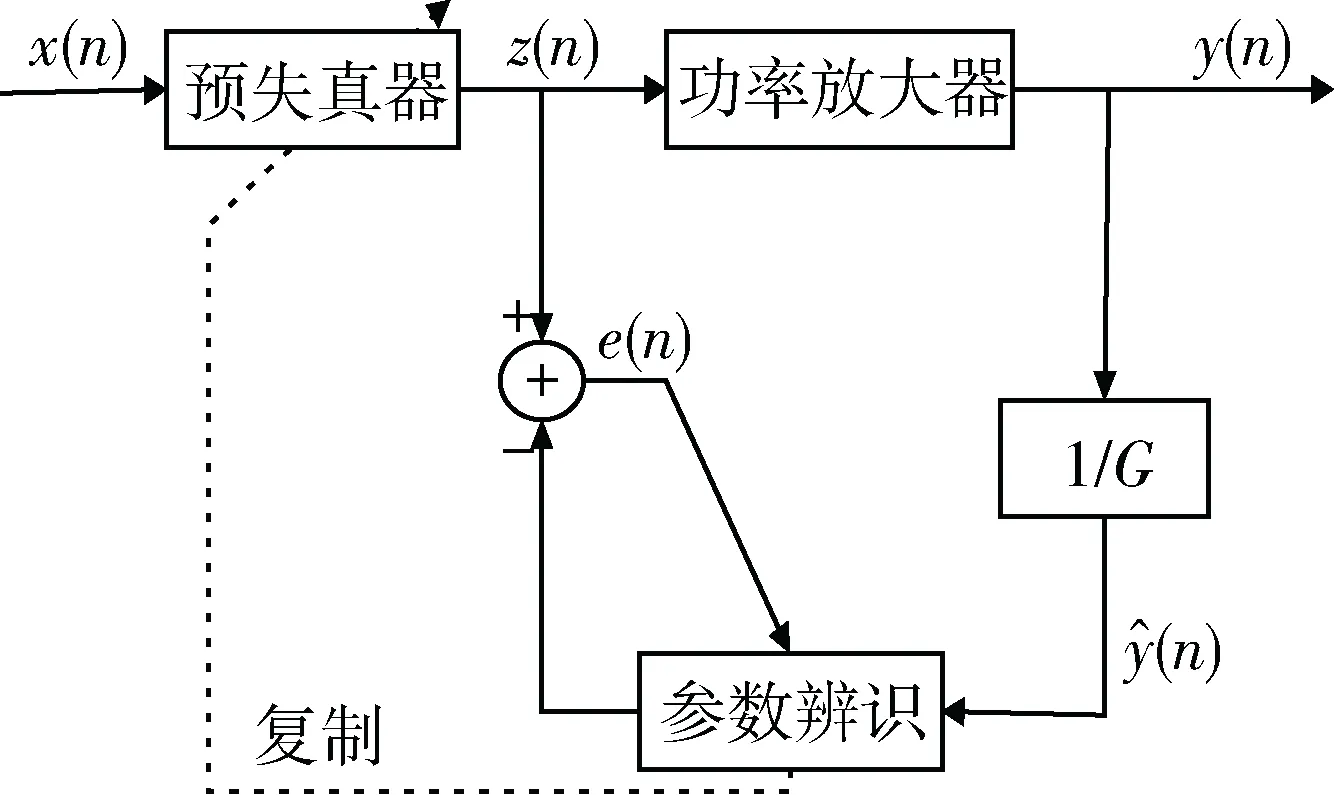
图1 数字预失真系统间接学习结构

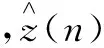
在MPM模型中，前置数字预失真器的输入x(n)与输出z(n)的行为模型可以表示为：

(3)

其中ωkm是前置预失真器的待辨识参数。

(4)

为简化表达，式(4)可以表示为矩阵形式：

(5)

其中后置预失真器辨识参数矩阵可表示为：

Ω(n)=[ω10,ω30,…,ωK0,…,ω1M,ω3M,…ωKM]T

(6)

后置预失真器输入矩阵可表示为：

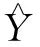
(7)

3 参数辨识-改进LMS算法

自1959年WIDROW B等人提出LMS算法[13]以来，因为其具有计算复杂度低、性能稳定、硬件易实现等优点，被广泛应用于各种自适应算法中。LMS算法主要是基于随机梯度下降来实现代价函数最小化，传统的LMS算法主要包括三个步骤：

(1)滤波输出对输入的响应：

y(n)=ωT(n)x(n)

(8)

(2)比较输出和期望产生误差信号：

e(n)=d(n)-y(n)

(9)

(3)根据优化算法迭代产生辨识参数：

ω(n+1)=ω(n)-μ(n)e(n)x(n)

(10)

其中μ(n)表示迭代步长，参数μ(n)的选择关系到算法的收敛性，当μ(n)较大时会加快收敛速度，但稳态误差大；当μ(n)较小时稳态误差小，但是收敛速度慢。收敛速度和稳态误差在LMS算法中是一对矛盾体，因此μ(n)收敛步长的合理选择成为关键问题。目前人们提出了很多基于变化步长的改进LMS算法[14-16]，一种是建立误差信号与步长之间的非线性函数关系，另一种是利用自适应过程中的梯度信号，以此来同时获得较快的收敛速度和较小的稳态误差，其主要思想是根据不同时间对收敛速度的需求来动态调整步长大小，即在算法收敛阶段采用较大的步长提高收敛速度，而在算法收敛后采用较小的步长来减小稳态误差。

在MP模型中，误差函数可以表示为：

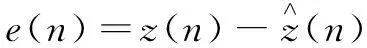
(11)

根据经典的LMS算法，损失函数可以表示为：

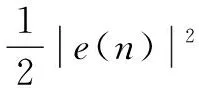
(12)

又因为损失函数的梯度可以表示为：

(13)

则预失真器待辨识参数的迭代公式可以表示为：

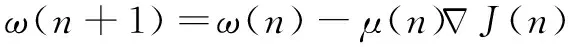
(14)

即

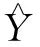
(15)

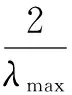
因为当输入大能量信号时，失真也会增大，因此可以通过归一化LMS来解决梯度噪声放大问题，提高收敛速度。归一化LMS算法可以表示为：

(16)

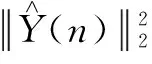
覃景繁等人[17]提出了一种基于Sigmoid函数变步长最小均方算法(Sigmoid Variable Step Least Mean Square, SVSLMS)，其变步长因子函数为:

(17)

式中:c值控制步长曲线的上升速度，而β值控制补偿曲线的最大高度。在误差e(n)较大的初始阶段该步长因子较大，收敛速度较快；当进入误差e(n)较小的稳态阶段后，步长值变小，而稳态误差也较小。但是当算法进入收敛阶段后，步长变化越来越剧烈，对算法性能产生振荡影响。

在文献[9]中提出了一种新的变步长因子:

μ(n)=υ·erf(1-e-α|e(n)|)

(18)

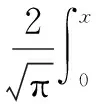
该变步长因子运用高斯误差函数建立基于输入函数和瞬时误差的变步长函数，相对传统的LMS、NLMS(Normalized LMS)和GNGD(Generalized Normalized Gradient Descent)算法[18]，基于高斯误差函数的MLMS算法收敛速度和稳态误差均得到提升，且在算法收敛后步长变化较为平稳。 但该算法过度依赖瞬时误差，对算法整体误差变化考虑不够，而且在算法收敛初始阶段，步长并不能达到最大控制因子υ的值，因此算法有待进一步改进。

以上两种基于归一化LMS算法的变步长因子各有优势，且均与反馈误差有关，当误差较大时，采用较大的步长来加快收敛速度，当误差较小时采用较小的步长来降低稳态误差，提升算法性能。

假设SVSLMS算法中参数β=2,c=1，MLMS算法中υ=1,α=1，得到两种算法步长变化对比曲线如图2所示。

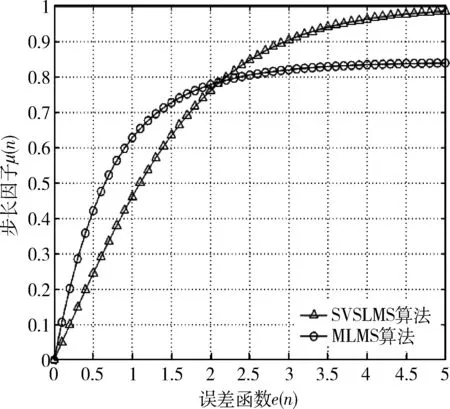
图2 SVSLMS算法与MLMS算法步长曲线对比

由图2可以看出，两条曲线均满足变步长LMS算法的要求，但各有优势，在误差较大时，SVSLMS算法具有更大变化的步长，在误差变小算法进入收敛后，MLMS算法步长减小更加平稳，因此综合考虑两种变步长算法的特点，在前面建立的功率放大器预失真模型的基础上提出一种改进的变步长LMS预失真自适应算法，在误差较大时，选择SVSLMS算法得到较快的收敛速度，而在算法收敛趋于稳定后，选用下降较为平稳的MLMS算法。改进的SVS-MLMS算法步长因子为：

(19)

其中β,c,υ,α为步长控制因子，分别控制曲线的最大步长和变化率，e0为步长函数转换因子，可以选取两条曲线的交点对应的误差值为参考值进行调整。

改进的SVS-MLMS算法是一个由四个参数控制的非线性函数，其曲线如图3所示，在图3中通过改变四个参数的取值可以得到不同性能的变步长LMS自适应算法。综上所述，本文提出了一种改进的变步长LMS自适应功率放大器预失真算法，具体如下：

(20)

式中：β,c,υ,α为步长函数μ(x)的控制调整参数。

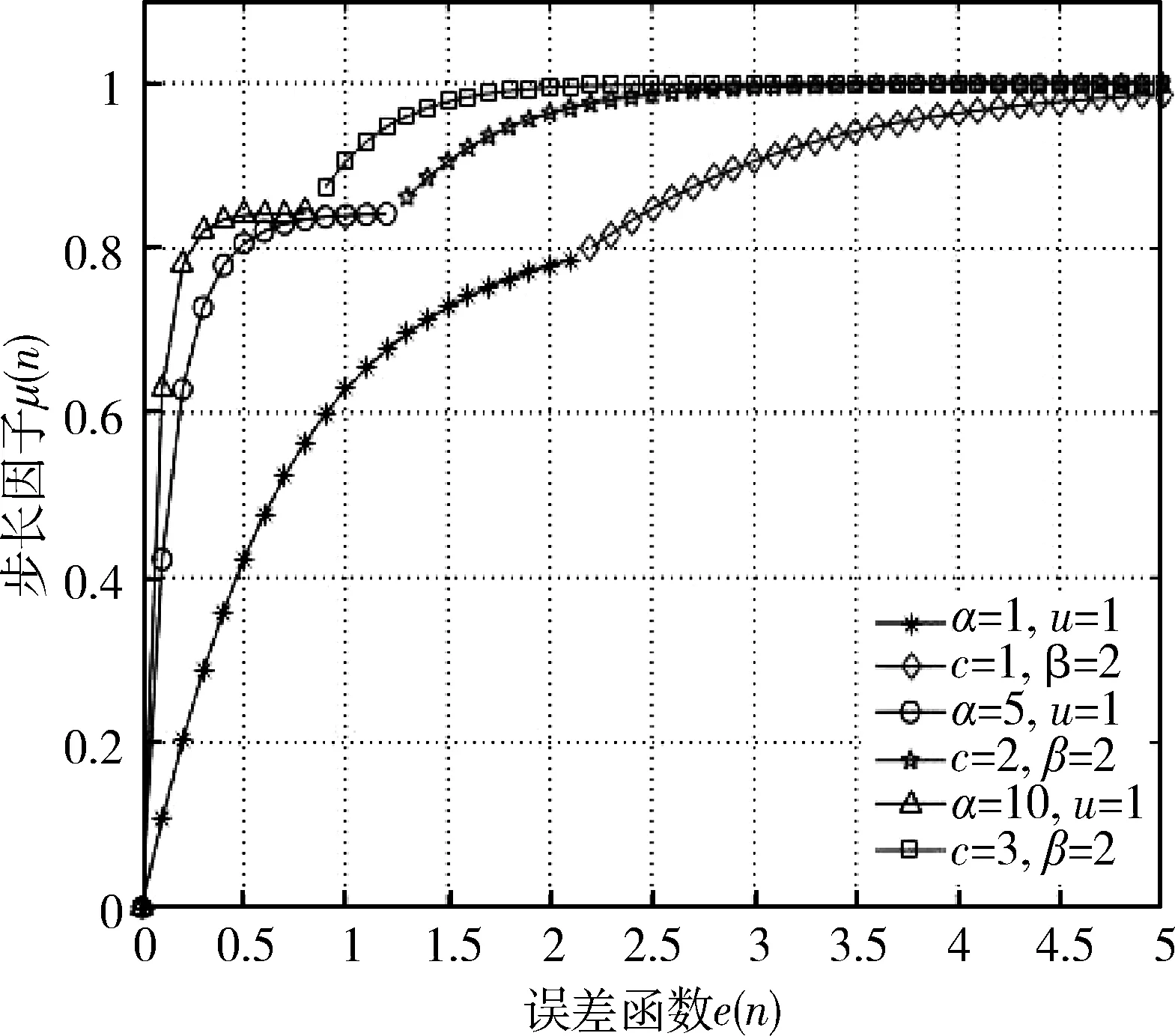
图3 控制参数变化下的改进SVS-MLMS算法步长曲线

4 仿真验证及分析

在间接学习结构下，采用前文基于Volterra级数简化的MP模型为功放预失真模型，采用归一化均方误差(Normalized Mean Square Error，NMSE)来验证模型准确度，NMSE表达式如下：

(21)

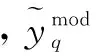
为了验证改进的SVS-MLMS算法在自适应预失真器中收敛速度和稳态误差的优势，下面采用APSK调制，发送滤波器和匹配滤波器的过采样因子为6，滚降系数为0.5，预失真阶数为4，记忆深度8，采样点数为1 000，通过独立统计蒙特卡罗平均得到归一化均方误差NMSE曲线。SVS-MLMS算法中参数取值分别为：β=1,c=1,υ=1,α=1。比较改进的SVS-MLMS算法与传统LMS、SVSLM算法和MLMS算法在归一化均方误差NMSE方面的差异，如图4所示，可以看出，经过3 000次迭代后LMS算法收敛到-26 dB，SVSLMS算法收敛到-37 dB，而MLMS算法和改进的SVS-MLMS算法要更加优于前面两个算法，分别收敛到-50 dB和-53 dB。因此对比结果表明，改进的SVS-MLMS算法具有更快的收敛速度和更小的归一化均方误差。

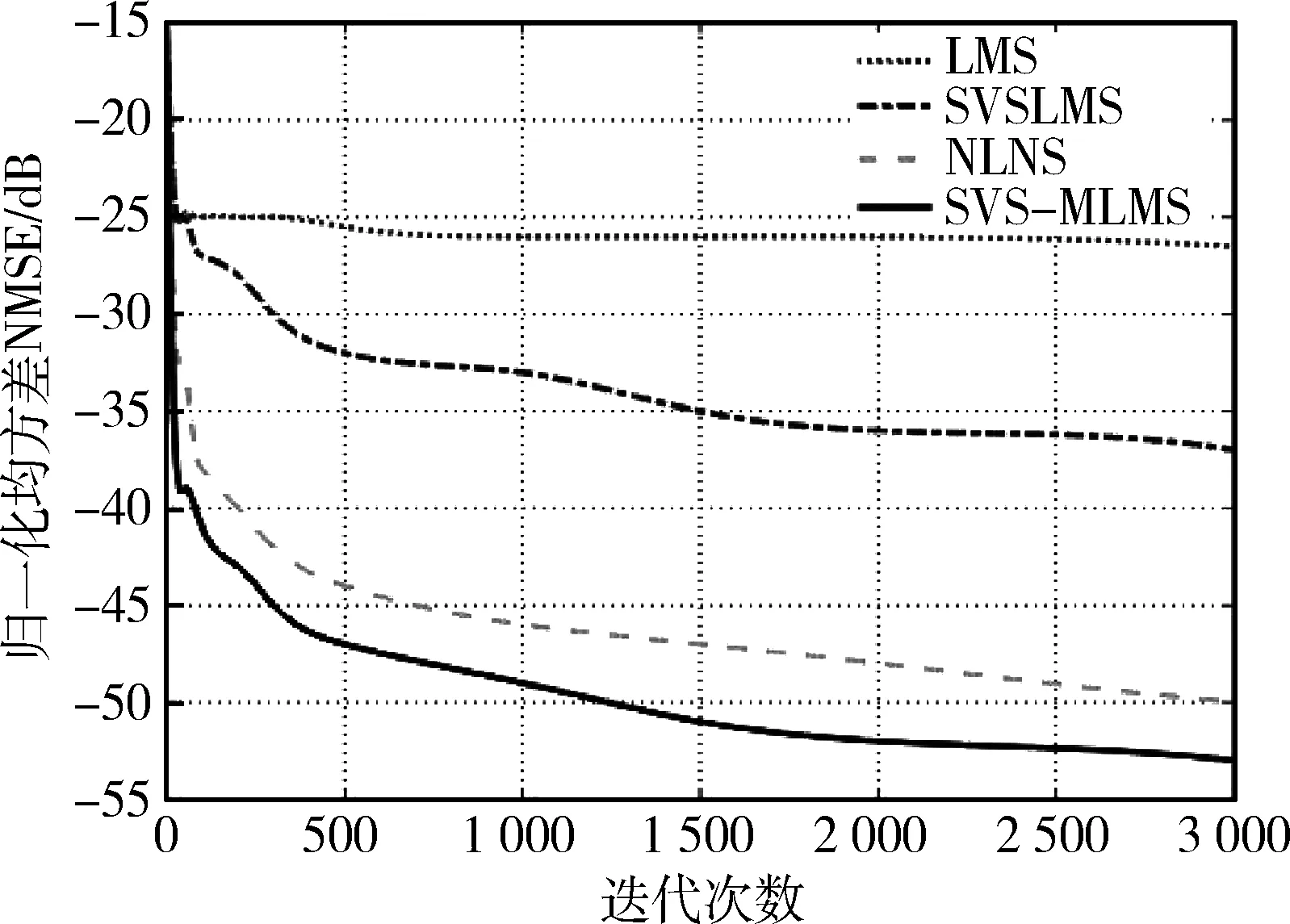
图4 改进算法与其他算法间NMSE对比

5 结论

在功率放大器数字预失真中，分析现有的各种变步长LMS算法的优势和劣势，提出了一种改进的SVS-MLMS预失真自适应算法。该算法通过组合SVSLMS算法和MLMS算法得到一种改进的变步长非线性函数。通过仿真发现，无论从收敛速度和归一化均方误差，改进的SVS-MLMS算法都要优于LMS算法、SVSLMS算法和MLMS算法，在收敛初期采用SVSLMS算法得到变化更大的步长，可以加快收敛速度，在算法收敛后采用MLMS算法得到更加平稳的步长变化函数，使得稳态误差较小，从而在数字预失真过程兼顾自适应算法的收敛速度和稳态误差，具有良好的算法性能。

[1] GILABERT P L, MONTORO G, BERTRAN E. On the wiener and Hammerstein models for power amplifiers predistortion[C]. Asia-Pracific Microwave Conference, 2005, 2: 4.

[2] 曹新容，黄莲芬，赵毅峰.一种基于Hammerstein模型的数字预失真算法[J].厦门大学学报(自然科学版)，2009, 48(1):1031-1034.

[3] SILVEIRA D, GADRINGER M, ARTHABER H, et al. RF-power amplifier characteristics determination using parallcl cascade wiener models and pseudo-inverse techniquer[C]. Asia-Pacific Microwave Conference, 2005,1: 4.

[4] SILVEIRA D D, ARTHABER H, GILABERT P L, et al. Application of optimal delays selection on parallel cascade hammerstein models for the prediction of RF-power amplifier behavior[C]. Asia-Pacific Microwave Conference, 2006:283-286.

[5] GOODMAN J, HERMAN M, BOND B, et al. A log-frequency approach to the identification of the Wiener-Hammerstein model[J]. IEEE Signal Processing Letters, 2009, 16(10):889-892.

[6] KIM J, KONSTANTINOU K. Digital predistortion of wideband signals based on power amplifier model with memory[J]. Electronics Letters, 2001, 37(23):1417-1418.

[7] MORGAN D R, Ma Zhengxiang, KIM J, et al. A generalized memory polynomial model for digital perdistortion of RF power amplifiers[J]. IEEE Transactions on Signal Processing, 2006, 54(10):3852-3860.

[8] Zhu Anding, PEDRO J C, BRAZIL T J. Dynamic deviation reduction-based Volterra behavioral modeling of RF power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 54(12):4323-4332.

[9] ZHANG F, Wang Yunhai, Ai Bo. Variable step-size MLMS algorithm for digital predistortion in wideband OFDM systems[J]. IEEE Transactions on Consumer Electronics, 2015, 61(1):10-15.

[10] 曾德军,石栋元,李金政,等. 基于双核NiosⅡ系统的数字预失真器设计[J]. 电子技术应用,2012,38(6):10-12.

[11] 李明,黄华,夏建刚.基于自适应均衡器的LMS和RLS算法仿真分析[J].微型机与应用,2009,28(20):56-58.

[12] TSIMBINOS J, LEVER K V. Computational complexity of Volterra based nonlinear compensators[J]. Electronics Letters, 1996, 32(9):852-854.

[13] WIDROW B, MECOOL J M, LARIMORE M G, et al. Stationary and nonstationary learning characteristics of the LMS adaptive filter [J]. Proceedings of IEEE, 1976, 64(8):1151-1162.

[14] RAYMOND K H, JOHNSTON E W. A variable step size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992, 40(7):1633-1642.

[15] Gao Ying, Xie Shengli. A variable step size LMS adaptive filtering algorithm and its analysis[J]. Acta Electronica Sinica, 2001, 29(8):1094-1097.

[16] MAYYAS K. A variable step-size selective partial update LMS algorithm[J]. Digital Signal Processing, 2013, 23(1):75-85.

[17] 覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997,12(3):171-194

[18] MANDIC D P. A generalized normalized gradient descent algorithm[J]. IEEE Signal Processing Letter, 2004, 11(2): 115-118.

Research on LMS adaptive algorithm for digital pre-distortion based on improving variable step size

Wang Linna1, Liu Ling1, Yang Xin2

(1. School of Electronical and Information Engineering, Sichuan Technology and Business University, Chengdu 611745, China;2. The Key Lab of Cloud Computing and Intelligent Information Processing, Sichuan Technology and Business University, Chengdu 611745, China)

In the process of digital pre-distortion, to deal with the shortcoming of the slower convergence speed and larger steady-state error in typical LMS adaptive algorithm，by analyzing the strengths and weaknesses of various improved Least Mean Square (LMS) algorithms, a normalized variable step-size LMS digital pre-distortion algorithm with combination of curve is proposed. The simulation results show that the proposed algorithm can improve performance extremely and ensure the accuracy of pre-distortion.

pre-distortion; Least Mean Square (LMS); variable step-size; normalization

TN722.7

A

10.19358/j.issn.1674- 7720.2017.20.023

汪琳娜，刘玲，杨新.改进变步长LMS自适应预失真算法研究[J].微型机与应用，2017,36(20)：80-83,91.

四川省教育厅科研项目(15ZB0458)； 四川工商学院科研项目(2016ZYB17X)

2017-03-30)

汪琳娜(1986-)，女，硕士研究生，讲师，主要研究方向：非线性信号处理和三支决策等。

刘玲(1978-)，女，硕士研究生，讲师，主要研究方向：电力电子与电力传动等。

杨新(1981-)，通信作者，男，硕士研究生，副教授，主要研究方向：数据挖掘，粗糙集及三支决策。E-mail:yangxin2041@163.com。