客流量对城市轨道交通网络易损性的影响研究*

蔡 虹 朱金福 徐腾飞

(南京航空航天大学民航学院1) 南京 211106) (南京工业大学经济与管理学院2) 南京 210094) (西南交通大学桥梁工程系3) 成都 610031)

客流量对城市轨道交通网络易损性的影响研究*

蔡 虹1,2)朱金福1)徐腾飞3)

(南京航空航天大学民航学院1)南京 211106) (南京工业大学经济与管理学院2)南京 210094) (西南交通大学桥梁工程系3)成都 610031)

采用考虑轨道交通网络特点的广义旅行时间模型结合基于Logit的随机用户均衡模型，分析了城市轨道交通网络站点间的旅行时间.将该旅行时间代入传统易损性的拓扑分析方法，建立了考虑站点能力限制的城市轨道交通网络易损性分析方法.利用该模型，可以定量的衡量:城市轨道交通网络各站点遭受不同模式的突发事件的破坏时的易损性.并以2008年北京市地铁网络为例，分析了客流量对城市轨道交通网络易损性的影响.结果表明，城市轨道交通的客流量规模与灾后站点破坏引发的流量重分配效应，都将影响各站点的易损性大小与易损性排序；特别是当网络客流量规模整体较大时，交通需求模式变化将显著影响各个站点的易损性指标；城市轨道交通网络站点的破坏程度与站点的易损性指标呈现非线性的正相关性.

轨道交通网络；易损性；Logit算法；随机用户均衡模型;拥堵效应

0 引 言

易损性(vulnerability)的概念越来越多地被用于定量研究突发事件对交通网络性能的影响.因为与可靠性(reliability)相比，易损性分析更关注于灾害发生后的后果，并不将突发事件发生概率纳入研究，而是假设突发事件必将发生，因此易损性分析也常被称为条件易损性分析[1-2].

国内外学者针对公路网易损性分析，在定义与定量计算方面开展了深入的研究工作.Deste等[3]分别从网络节点的可到达性(accessibility)与广义旅行时间的增加程度定义易损性.目前易损性虽然没有形成明确统一的定义，但经过多位学者的不断研究与实践，其内涵已经被众多学者接受，Mattsson等[4]进一步将其描述为：易损性是对各类风险造成的交通系统的瘫痪或者劣化程度的描述.可以通过比较不同场景下的路网性能，来描述灾害对路网的影响.

在易损性定量分析中网络拓扑分析被应用于易损性分析中[5-7].此外，Chen等[8]研究了出行者出行模式与网络流量的不同对路网易损性的影响；张勇等[9]通过测定公路网络的鲁棒性指数来辨识路网的易损性；刘思峰等[10]提出了重要路段的辨识模型；杨露萍等[11]将路网用户最终损失时间作为量度进行公路网络易损性衡量.

总的来说，交通路网易损性分析方法可以分为两类：拓扑易损性分析与交通系统易损性分析.拓扑易损性分析方法利用图论知识，借助交通网络损坏前后的拓扑特征变化(如效率、节点度、介数、强度，网络直径等)来分析易损性[12]，此分析方法能够快速、准确的抓住交通网络的静态特征，但是无法真实反映交通流量及拥堵效应对交通网络的影响；而交通系统易损性分析方法则更多的从真实的交通需求与供给能力出发，通过分析交通网络中的旅行时间或运输能力来分析易损性，但需要较为复杂的建模工具与技巧，计算规模偏大.

针对上述交通路网易损性分析方法的不足，本文提出将拓扑易损性分析中节点间的平均距离替换为广义旅行时间，籍此反映流量对交通网络性能的影响.并根据文献[4]对于交通网络易损性的定义将城市轨道交通网络站点损坏定义为灾害场景；将城市轨道交通网络中站点间最短广义旅行时间的变化率定义为易损性指标.针对轨道交通网络特点，建立了适用于城市轨道交通系统的时间拥堵模型；据此结合基于Logit的随机用户均衡模型计算各OD对之间的广义旅行时间，进而计算网络效率；然后通过比较城市轨道交通路网受损前后路网效率的变化率来计算易损性；最后，通过调整参数来模拟不同交通流量下城市轨道网络易损性的变化规律.

1 城市轨道交通广义旅行时间模型

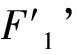
tN1,1,N2,1=tN1,1,F1+tF1,N2,1+Tf

(1)

式中：tN1,1,F1为从N1,1到F1的时间；tF1,N2,1为从F1到N2,1的时间.

图1 换乘站的虚拟节点与链

在城市轨道交通系统中，两站点间的运行时间是与客流量无关的恒量，其由列车时刻表确定.而拥堵效应导致的旅行时间增长是由起点候车时间和换乘时间共同决定的.

列车行车间隔(Tc)定义为相邻两列车离开站点的时刻或相邻两趟列车的到达时间间隔[14].对于乘客而言，其等待时间Tw为乘客到达站台直至列车离开站台的时间.在公共交通系统中，等待时间的数学期望EX(Tw)取决于平均行车间隔EX(Tc)与行车间隔的变异系数Var(Tc)

(2)

当行车间隔小于某一阈值时，乘客到达站台的时间可以假设为平均分布.地铁网络平均行车间隔小于公交车行车间隔，且因严格按照列车时刻表运行，其行车间隔的变异性系数可以假设为0，因此，乘客的平均等待时间为0.5Tc.

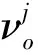
(3)

式中：[f]为截尾函数，表示仅取函数f的整数部分.

换乘的便利性会在很大程度上影响乘客的路径选择.一般情况下，乘客倾向于选择换乘次数较少的线路.本文引入惩罚系数模拟这种选择倾向[15].因此广义换乘时间可以表达为

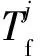
(4)

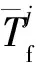
综合考虑：列车运行时间Tta，候车时间和换乘时间，路径i上的广义旅行时间为

(5)

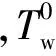
2 基于Logit的随机用户均衡模型

用户均衡模型(user equilibrium,UE)将路径选择抽象为凸函数优化问题，其目标函数为

(6)

式中：

∀r∈R,s∈S

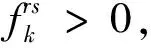
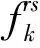
(7)

为模拟乘客对路网信息判断的随机性，基于随机用户均衡模型(stochastic user equilibrium, SUE)，采用Logit模型考虑用户的路径选择概率为[16]

(8)

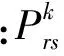
3 城市轨道交通网络易损性计算方法

利用考虑运输能力的广义旅行时间模型，可将路网效率定义为

(9)

式中：n为节点的数量；ρij为节点对(i，j)间最小广义旅行时间.

当轨道交通网络站点发生损坏时，一方面由于站点的损坏会导致节点对间连通性下降，延长广义旅行时间；另一方面乘客的路径重新选择行为，会导致其余站点的流量重分配，从而可能引发站点堵塞，也将延长广义旅行时间.最终，某一站点的损坏，将降低整个轨道交通路网的效率.

城市轨道交通网络易损性计算流程描述为：

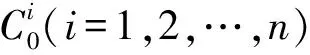
步骤2采用基于Logit的路径选择均衡模型分配流量.

步骤3按照式(9)计算正常轨道交通网络系统的路网效率E(G).

步骤4初始化站点编号i=1.

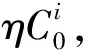
步骤6检查受损轨道网络的每个OD对的联通性.如果不联通，假设乘客会选择最近站点换乘.

步骤7采用基于Logit的随机用户均衡模型重新分配流量.

步骤8按照式(9)计算受损轨道交通网络系统的路网效率E(D).

步骤9计算站点i受损后的易损性

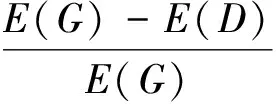
(10)

步骤10如果站点数量i小于总的站点数n，则令i=i+1,并返回到步骤5；否则计算结束.

4 算例分析

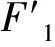
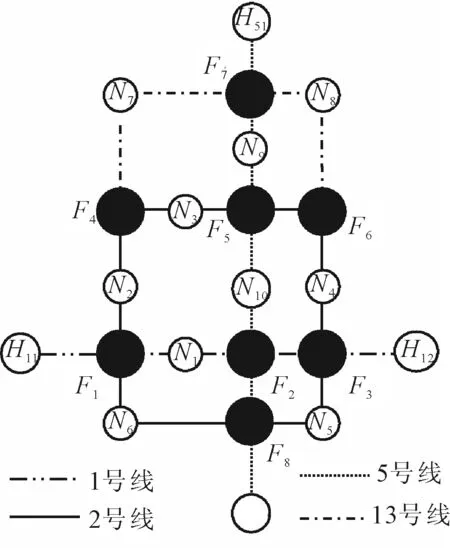
图2 北京地铁网络图

表1 OD流矩阵 千人/h

地铁的发车间隔和平均停站时间分别设为5 min和2 min；换乘惩罚系数γ为1.86；Logit流量分配算法中的参数θ为20；每个运行周期单趟列车的容量为2 460定员.

针对地铁网络中各主要换乘站点分别发生灾害丧失功能的场景，利用本文模型，可以计算各换乘站点的易损性指标，结果见图3的C3工况.由图3可知，C3工况中换乘站点的易损性指标明显大于C1工况(不考虑客流量信息的纯粹拓扑易损性分析方法结果)与C2(考虑初始交通网络的客流量信息，但不考虑灾后乘客路径重新选择后的客流量重分配情况)工况.这说明：在城市轨道交通网络中，不仅较大客流量产生的拥堵效应对站点易损性指标有影响；同时，在突发情况下，由于部分站点功能丧失导致的客流量重分配效应也将加剧其余未损站点的客流量与拥堵效应，从而进一步影响站点易损性指标.

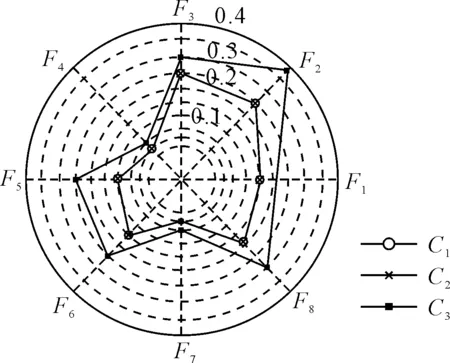
图3 北京地铁网络换乘站易损性

为考虑换乘站中仅上行或者下行线路丧失运输能力的情况，本文计算了换乘站虚拟节点的易损性指标，见图4.本文特引入OD需求比例参数λ来调整OD需求矩阵，以描述不同OD需求规模.特别的，当λ=0时，本模型计算的易损性指标将退化为拓扑易损性指标.表2为λ=0，1.0，2.0时，各换乘站点的易损性指标及易损性排名。由表中可以看出，交通流量的规模，不仅改变各个站点易损性指标，也将改变站点的易损性排序.

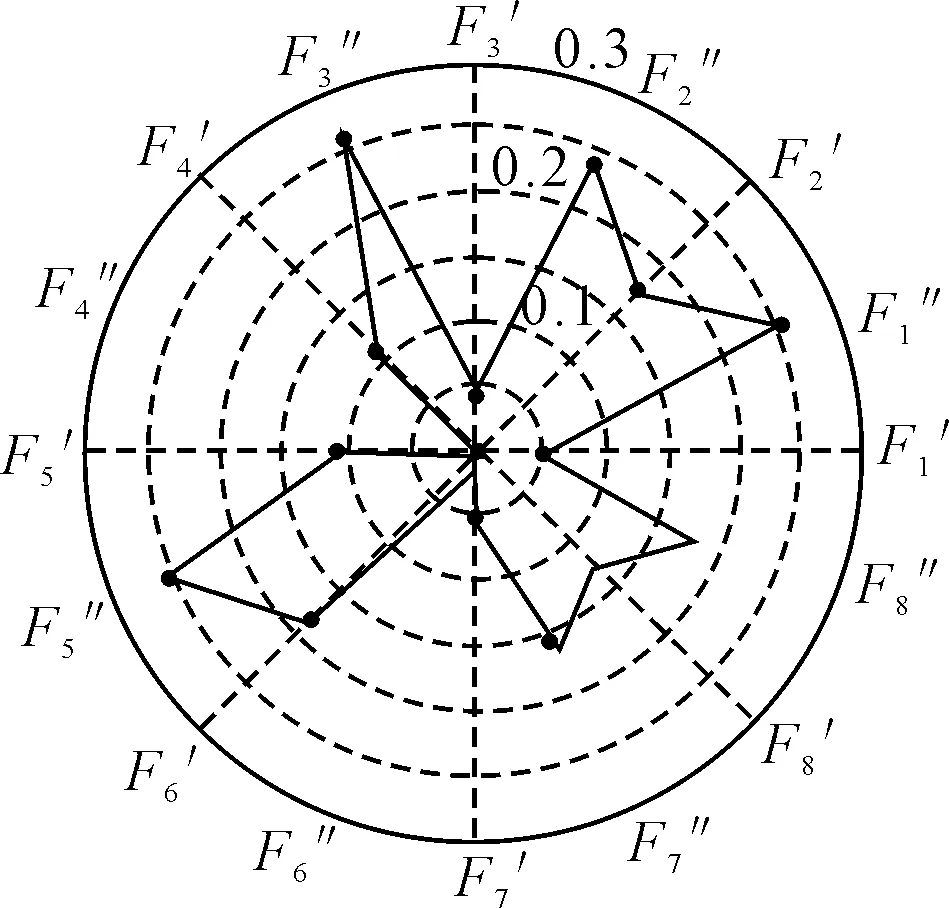
图4 换乘站单条线路完全受损条件下的易损性

针对具体站点，图5为F2与F4的易损性指标随着客流量规模变化的情况.总的来说，站点易损性随着客流量规模的增大而增加，但不呈现线性趋势；值得注意的是，客流量规模对每个站点易损性的影响程度不同，F2比F4的易损性变化明显，上升速率更快.

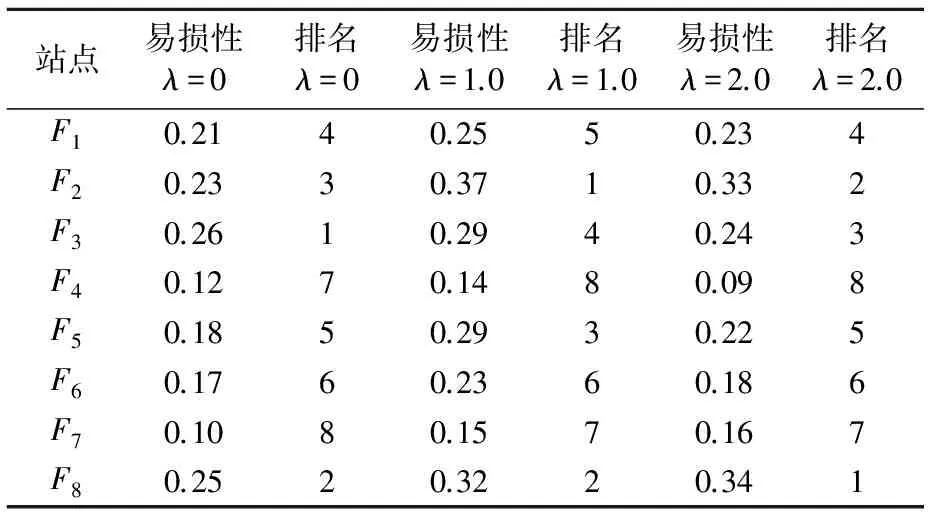
表2 换乘站点的易损性指标与排名

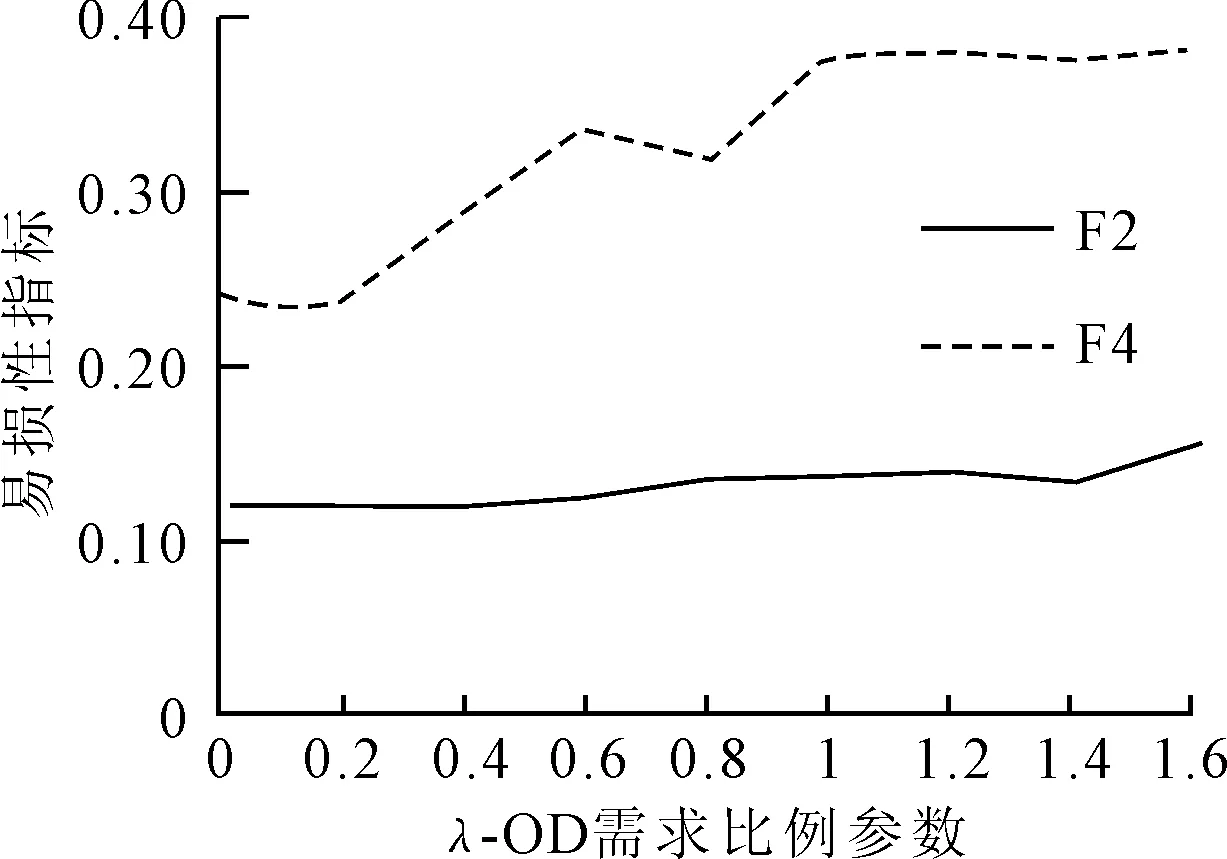
图5 换乘站F2及F4在不同流量下的易损性

如果将OD-1矩阵中的(F1,H12)和(F1,H6)的数据做交换得到新的需求矩阵OD-2，并计算OD-2模式下的换乘站易损性，并与OD-1需求矩阵的计算结果比较，见图6.计算结果表明，当λ的值较小即客流量不大的情况下，不同的OD模式下，对站点易损性影响不大；但是，当λ的值较大，不同模式下的OD流会使得站点易损性明显变化.这是因为，客流量较小时，地铁网络中拥堵效应不明显，因此OD模式改变不会显著影响易损性分析结果；而当客流量较大时，不同的OD需求模式将导致地铁网络中的拥堵状况明显改变，因此对站点的易损性分析有较大影响.

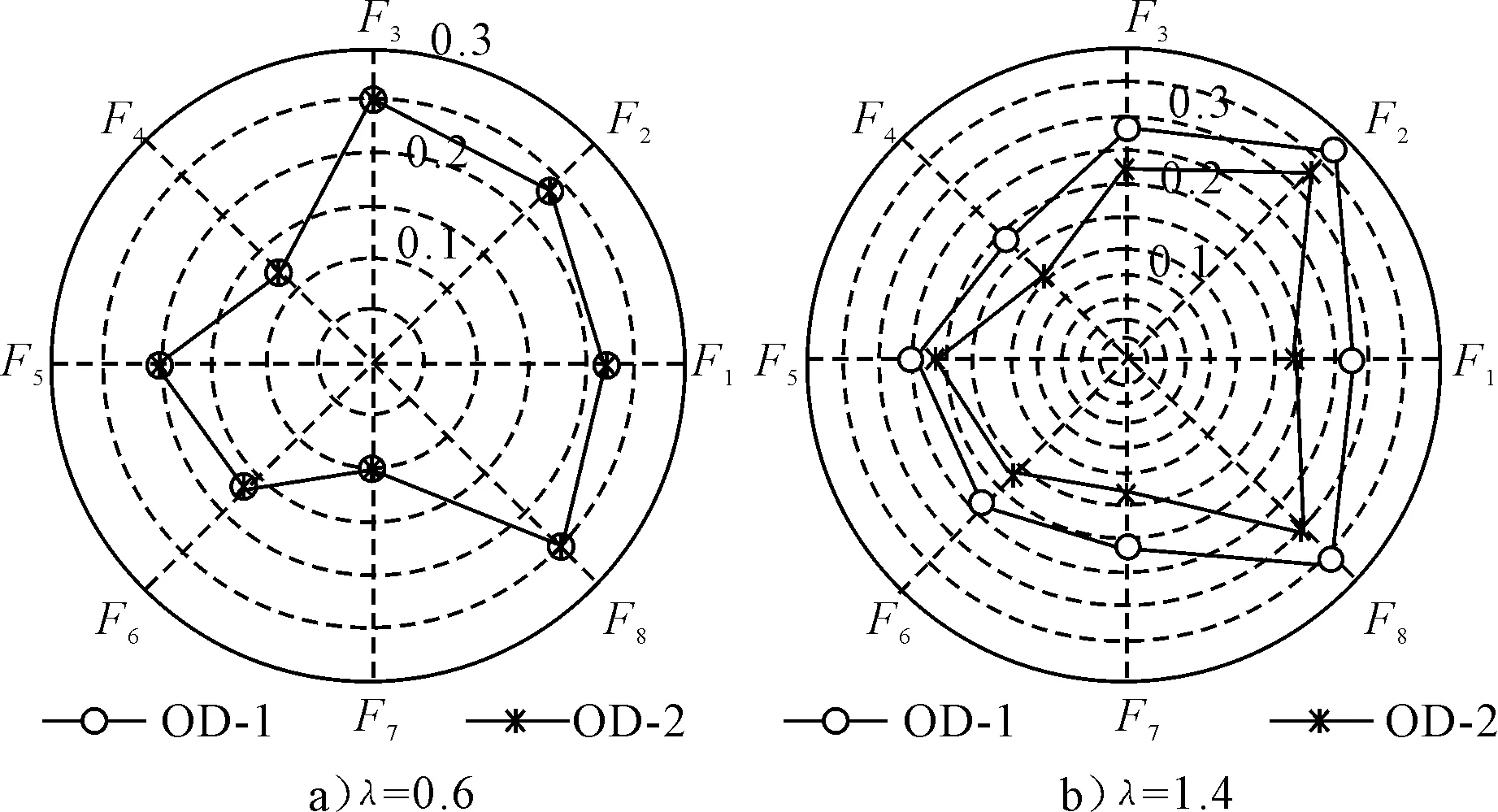
图6 北京地铁不同OD模式下的易损性

利用本文提出的模型，不仅可以计算出站点完全损坏时的易损性指标，利用参数η还可计算轨道交通站点部分损坏时的站点易损性指标。以站点F3与F6为例，图7为不同破坏水平下，站点的易损性指标的变化情况。由图7可知，站点破坏程度与易损性具有明显的正相关性，其次，站点破坏程度与易损性的呈现非线性关系.

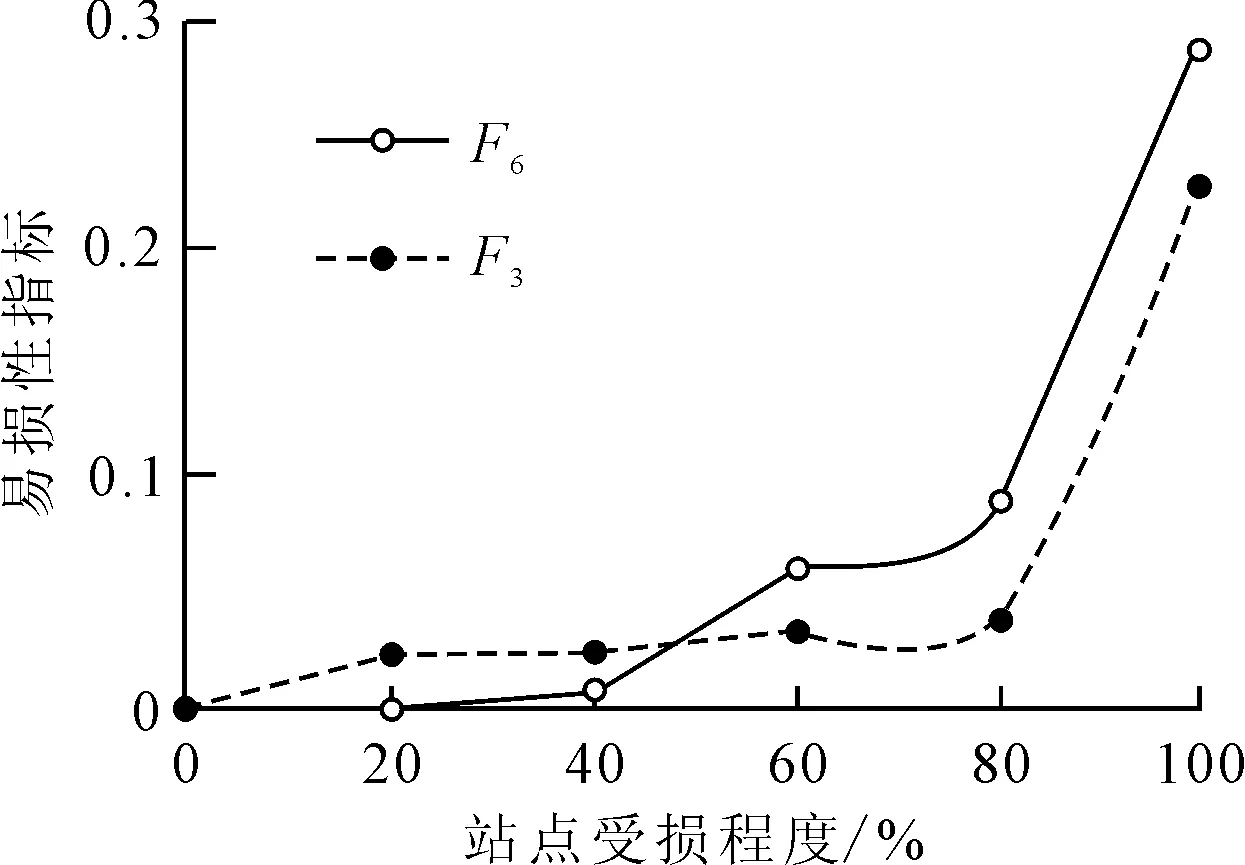
图7 不同破坏程度下的换乘站F3，F6易损性分析

5 结 论

1) 城市轨道交通的日常客流量规模与灾后站点遭破坏所引发的客流量重分配效应，都将影响各站点的易损性与重要性.

2) 当交通路网中的客流量规模较大时，交通需求模式变化将显著影响各个站点的易损性指标；而当交通路网中客流量规模较小时，交通需求模式对各站点的易损性影响不明显.

3) 由于各个站点的易损性指标，受到客流量规模与需求模式的影响，因此，在利用易损性分析结果进行站点重要性排序以及政策决策中，应充分考虑不同场景或突发事件下的客流量规模与需求模式变化，进行综合判断.

4) 城市轨道交通网络站点的被破坏程度与站点的易损性指标呈现非线性的正相关性.

[1] JENELIUS E,MATTSSON L G.Road network vulnerability analysis:conceptualization, implementation and application[J]. Computers, Environment and Urban Systems,2015,49(1):136-147.

[2] JENELIUS E, PETERSEN T, MATTSSON L G. Importance and exposure in road network vulnerability analysis[J]. Transportation Research Part A: Policy and Practice,2006,40(7):537-560.

[3] DESTE G, TAYLOR M. Modeling network vulnerability at the level of the national strategic transport network[J]. Journal of the Eastern Asia Society for transportation studies,2001,4(2):1-14.

[4] MATTSSON L G, JENELIUS E. Vulnerability and resilience of transport systems—a discussion of recent research[J]. Transportation Research Part A,2015,81(11):16-34.

[5] CRIADO R, HERNANDEZ B B, ROMANCE M.Efficiency, vulnerability and cost: an overview with applications to subway networks worldwide[J]. International Journal of Bifurcation and Chaos,2007,17(7):2289-2301.

[6] YIN H Y, XU L Q. Measuring the structural vulnerability of road network: A network efficiency perspective[J]. Journal of Shanghai Jiaotong University (Science),2010,15(6):736-742.

[8] CHEN A, YANG C, KONGSOMSAKSAKUL S, et al.Network-based accessibility measures for vulnerability analysis of degradable transportation networks[J]. Networks and Spatial Economics,2007,7(3):241-256.

[9] 张勇，屠宁雯，陶骏杰.道路交通网络脆弱性动态辨识方法[J].交通运输工程学报,2014,26(5):74-81.

[10] 刘思峰，万寿庆，陆志鹏.复杂交通网络中救援点与事故点间的路段重要性评价模型研究[J].中国管理科学,2009,17(1):119-124.

[11] 杨露萍,钱大琳.道路交通网络脆弱性研究[J].交通运输系统工程与信息,2012,12(1):105-110.

[12] NAGURNEY A, QIANG Q. A network efficiency measure for congested networks[J]. EPL,2007,79(3):380-395.

[13] RODRGUEZ N E, GARCA P, JUAN C.Measuring the vulnerability of public transport networks[J]. Journal of transport geography,2014,35(1):50-63.

[14] XU X Y, LIU J, LI H Y. Probabilistic model for remain passenger queues at subway station platform[J]. Journal of Central South University,2013,20(3):837-844.

[15] SI B F, ZHONG M, ZHANG H Z. An improved dial’s algorithm for logit-based traffic assignment within a directed acyclic network[J]. Transportation Planning and Technology,2010,33(2):123-137.

[16] DENG Y L, LI Q M, LU Y. A research on subway physical vulnerability based on network theory and FMECA[J]. Safety Science,2015,80:127-134.

[17] 林湛，蒋明清，刘剑锋.城市轨道交通客流分配的改进Logit模型及方法[J].交通运输系统工程与信息，2012,12(6):145-151.

Influence Study of Passenger Flow Capacity on the Vulnerability of the Urban Rail Transit Network

CAIHong1,2)ZHUJinfu1)XUTengfei3)

(CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China)1)(EconomyandManagementSchool,NanjingTechUniversity,Nanjing210094,China)2)(DepartmentofBridgeEngineering,SouthwestJiaotongUniversity,Chengdu610031,China)3)

Combining the Logit based Stochastic User Equilibrium and Generalized Travel Time model for the urban rail transit, the travel time between the stations in the unban rail transit network was analyzed. A vulnerability analysis for the urban rail transit network incorporating the transport capacity constraint was presented in this paper by introducing the Generalized Travel Time into the traditional topological approach. Based on the model, the vulnerability of network in different emergency could be analyzed quantitatively. Moreover, the influence of passenger flow capacity on the vulnerability of Beijing metro network in 2008 was studied. The results show that both magnitudes of OD demand and passenger flow reassigning effect among stations after disaster have influences on the assessment of vulnerability index and ranking of each metro station. Especially, when the metro network was busy, the change of OD demand patterns would impact on the vulnerability of stations distinctly. Thus, a nonlinear positive correlation between the damage level of metro stations and vulnerability were found.

unban rail transit network; vulnerability; logit algorithm; stochastic user equilibrium; congestion effect

U121

10.3963/j.issn.2095-3844.2017.05.018

2017-08-01

蔡虹(1978—)：女，博士生，讲师，主要研究领域为城市交通运输与规划

*2016年度江苏省高校哲学社会科学研究一般项目(2016JB630029)、2016年南京工业大学青年社科基金项目(qnsk2016014)、2016年教育部社科基金未立项扶持项目(ZX17442520001)、国家自然科学基金项目(71671089，71171110，71371097)资助