基于超级网络的空铁联合交通流分布模型*
2017-11-02戴福青庞笔照赵元棣
戴福青 庞笔照 袁 婕 赵元棣
(中国民航大学空中交通管理学院 天津 300300)
基于超级网络的空铁联合交通流分布模型*
戴福青 庞笔照 袁 婕 赵元棣
(中国民航大学空中交通管理学院 天津 300300)
针对城市间空铁旅客出行需求与交通供给运量不匹配造成运力闲置或运力不足的现状,研究了城市间空铁联合交通流分布问题.利用超级网络理论构建空铁联合运输超级路网,建立路网中节点和路段阻抗函数,在此基础上设计了基于路段综合阻抗的权重模型和交通流分布模型,利用Floyd算法对模型进行求解,以上海—北京为例进行了算例分析.结果表明,模型可对城市间空铁联合运输路网的交通流分布进行有效计算;通过与现行投入运量对比,有关部门可合理调配运力资源,优化路网运力分布,解决交通供给量与实际运力不匹配问题.
空铁联运;超级路网;交通流分布;阻抗函数;Floyd算法
0 引 言
空铁联合运输结合铁路站点多、运量大和航空远距离快速直达等优点必将得到全面发展.而空铁联合交通流分布是相关部门进行运力投放、运输线网规划以及合理配置运力资源的重要决策依据[1].
国内外学者对此进行了研究,Okumura等[2]从旅客出行便利性角度出发,利用遗传算法设计了最优空铁联运网络;Behrens等[3]建立嵌套混合Logit模型,分析了伦敦到巴黎航空和高铁市场旅客出行行为,结论表明出行费用和便利性影响旅客出行选择;Pellegrini等[4]从空铁联合路网规划角度,讨论了空铁联合运输系统的容量,为欧洲单一天空和单一高铁路网建设提供决策依据.刘祯根等[5]分析了交通分布-交通分配组合模型,并结合实例提出组合模型求解算法;朱法勇等[6]根据静态多路径分配思想,建立综合阻抗函数,研究并验证了铁路专线客流的分配模型;王素欣等[7]考虑交通拥挤程度,改进了BRP路阻计算方法;孟梦等[8]将超级网络理论引入城市道路交通研究领域,构造组合出行模式超级交通网络,并建立了数学模型.
然而,以上方法大多从局部讨论联运线路设计和换乘枢纽选择等问题,或单一研究铁路专线交通流的分布,缺乏对城市间空铁联合交通流分布的整体性研究.结合空铁联运线路复杂和旅客出行影响因素繁多两方面设计了一种空铁联合运输超级路网,在此基础上,建立了空铁联合交通流分布模型,并给出模型求解算法,最后用算例验证了模型的实用性和有效性.
1 空铁联运超级网络模型
高铁和航空作为两种运输方式在速度、旅客类型和出行费用等方面联系紧密,而普通铁路与上述二者差异较大.因此,仅研究高铁和航空旅客运输交通流在城市间的分布.
高铁和航空运输网络结构通常由节点及节点间的边组成,节点代表载运工具停靠点,边代表具有通行容量、通行时间及通行费用的运输段.随着高铁路网、航路网各自规模扩大且结构日益复杂,同时,旅客出行方式多样化又使得二者联系更加紧密,单一路网无法全面描述组合出行模式下的联合网络特征.因此,引入超级网络理论[9],建立包含高铁路网和航路网的超级网络.
基于超级网络及其扩展理论将图1a)所示空铁单一路网结构转化为图1b)空铁超级路网结构.
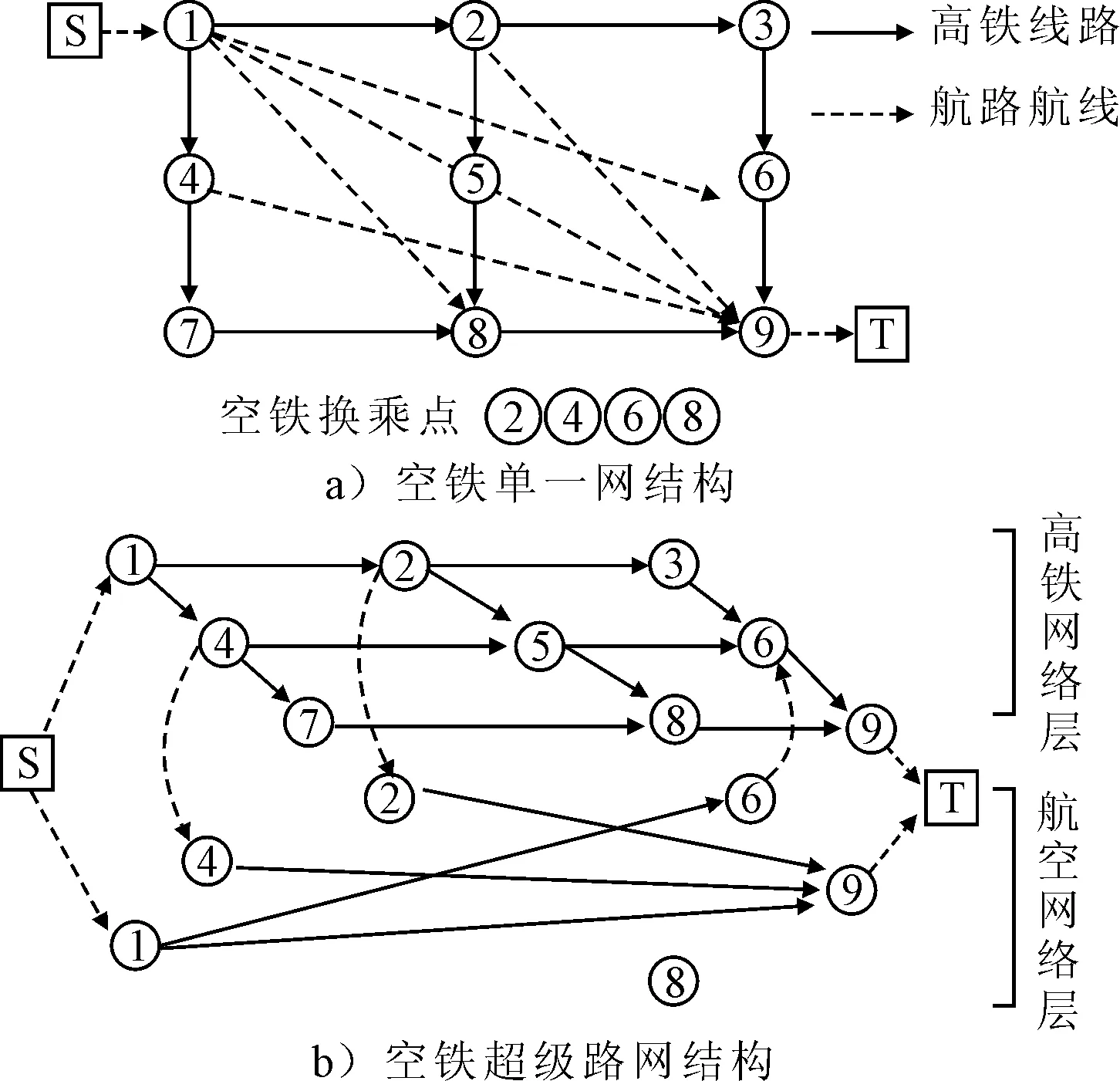
图1 空铁网结构
2 综合阻抗模型
2.1 路段阻抗模型
空铁超级路网中包含:高铁路段、航路段和换乘路段(高铁站和机场间路段).对于路段阻抗,在出行费用和出行时间基础上,引入引力场模型分析连接两个节点城市的路段阻抗.Tinbergen基于引力模型提出一个经济学模型[10],来分析两个经济体间的贸易流量,模型表示为
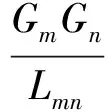
(1)
式中:Imn为引力值;Lmn为城市m和城市n之间距离;K为引力常数;Gm和Gn分别为城市m和城市n人均GDP.
人均GDP可以有效反映一个城市工商业、旅游等产业的活跃程度,影响交通运输业的发展,且人均GDP越大,旅客出行越注重时间成本,在引力场模型基础上改进路段阻抗函数,分析两个经济体之间的空铁交通流量.结合式(1)可得引力值倒数和路段通行时间构成时间成本阻抗;路段通行距离构成距离成本阻抗.路段阻抗函数表示为
(2)
式中:Dmnτ,Lmnτ和Vmnτ分别为节点m与n之间路段阻抗、距离(km)和平均通行速度,km/h,τ=1,2,3分别表示高铁路段、航路段和换乘路段的相应参数;μ为票价折扣率;φ和w分别为出行时间权重和出行费用权重;fT为路段单位时间费用,元/(人·h),fLmnτ为单位距离费用,元/(人·km).
2.2 节点阻抗模型
1) 不换乘节点阻抗 包括高铁直达和飞机直达经过的节点;高铁直达考虑过站停留时间ts;飞机直达无节点阻抗,因此,不换乘节点阻抗函数表示为
Dp=tsfT
(3)
式中:fT同上定义;Dp为高铁直达节点阻抗.
2) 换乘节点阻抗 包括空铁换乘、高铁换乘、飞机换乘三种模式.空铁换乘节点阻抗包含三个主要部分:出站时间、乘车时间和费用、进站等候时间;其中高铁出站时间和进站等候时间近似相等,机场候机时间与出机场摆渡车、等候提取行李等时间之和近似相等,它们之间关系见图2.

图2 空铁换乘节点阻抗关系
高铁和飞机换乘均为本场内换乘,节点阻抗中只含换乘时间成本,取高铁平均候车时间tC1,飞机平均候机时间tC2[11],tC1=0.5 h,ts=0.05 h,tC2=1 h.旅客中转换乘次数受出行时间、费用等因素影响且与出行距离密切相关,三种换乘方式对应换乘次数与出行距离关系见表1.

表1 换乘次数与出行距离关系
综上,建立换乘节点阻抗函数为
(4)
式中:fT同上定义;Dq为换乘节点阻抗;Lhc和Vhc分别为高铁站与机场之间距离(km)和换乘车辆平均行驶速度,km/h.
综合阻抗包括路段阻抗和节点阻抗,将相邻节点阻抗平均分配给连接相邻节点的路段,表示为
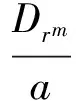
(5)
式中:D*mnτ为相邻节点m和n之间路段综合阻抗;Drm和Drn分别为节点m和n处的总阻抗,Dr=Dpxδ1+Dqxδ2,xδ1、xδ2为0-1变量且xδ1+xδ2=1;a和b分别为与节点m和n直接相连的路段个数.
2.3 最短线路阻抗
得到节点阻抗和路段阻抗,计算任意两个节点间的最短距离矩阵.其中,超级路网每条边的权值对应路段综合阻抗值.考虑到Floyd算法较Dijkstra算法对稠密图计算性能和计算结果更佳[12],适合空铁超级路网计算.该算法步骤如下:
1) 构造节点Vm一步到达节点Vn的阻抗矩阵D1=(D1mn)D1也是一步到达的最短距离矩阵.如果Vm和Vn之间无相连边,且不能换乘,则令路段阻抗Dmnτ=+∞.
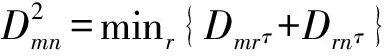
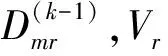
4) 比较矩阵Dk与Dk-1,当Dk=Dk-1时,即得任意两点间的最短距离矩阵Dk.
3 空铁联合交通流分布模型
3.1 路段权重模型
根据空铁超级路网和其中任意两点间最短距离矩阵,从起点S到终点T的方向依次计算每个路段的权重值.联合交通流按照路段对应权重进行分配.各路段初始权重W(m,n)τ与其对应阻抗成线性负相关,随路段数量增加单位路段权重减小,表示为
(6)
式中:Zr为路段数量;N为正整数.
(7)
式中:Ti为终点是i的路段起点集合,当达到终点T即i=T时,各路段权重计算完成.
3.2 交通流分布计算方法
根据路段权重计算交通流分布.首先将旅客出行总量按高铁、飞机和空铁联运三种出行方式对应权重进行分配;考虑载运工具单位运力性能(座位数)不同,进行归一化处理:
(8)
式中:M0为出行总量;Mτ为各出行方式从起点S到终点T的交通量总和;Gr为载运工具单位运力性能.
空铁联运交通量与高铁和航空交通量的平均增长率密切相关;同时还与票价成线性反比关系[13-15],空铁联运交通量增长关系式表示为
(9)
式中:M3为初始路段权重空铁联运交通流分布量,f(Mr)M3为空铁联运交通量与Mr(r=1,2)高铁和航空交通量增长率的函数关系.
得到三种方式交通量分布进行内部细分至各路段.从终点T到起点S的方向计算每个路段交通流分布量.节点n的交通量为E(m,n),m∈Ti,计算方程为
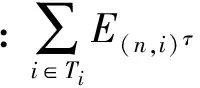
4 算例分析
选取上海至北京连线两侧各300 km范围内省会、直辖市及交通枢纽一级城市构建空铁超级路网,对联合交通流分布模型进行验证分析.
4.1 条件说明及参数标定
1) 计算交通流分布,暂不考虑路段和场站容量限制.
2) 空铁联运换乘一般只在起终点城市周边一定范围内进行,算例取起、终点换乘范围300 km.
3) 同一城市高铁站或机场数量2个及以上视为一个高铁站系统或机场系统,可得表2换乘路段距离.
4) 据2016年10月1日前开通的城际、高铁线路和航班运行线路,得表3高铁路段距离,表4飞行航段距离,结合表1得三种出行方式换乘次数:X=1,Y=1,Z=0,数据源自:2016版铁路运行图、2016版中国民航航路图.
5) 据各节点城市2015年人均GDP数据,见表5,算例取时间权重φ=0.5,费用权重w=0.5,引力常数k=10.路段单位时间费用fT由2015年底人均GDP换算得fT=28.75.
6) 取高铁、飞机和机场巴士平均运行速度分别为250,600和40 km/h;路段单位距离费用fLmn1=0.5,fLmn2=0.75,fLmn3=1.8;飞机平均运力180座/架;标准高铁列车CHR3定员610座/列;机场巴士30座/辆.

表2 空铁换乘路段距离 km
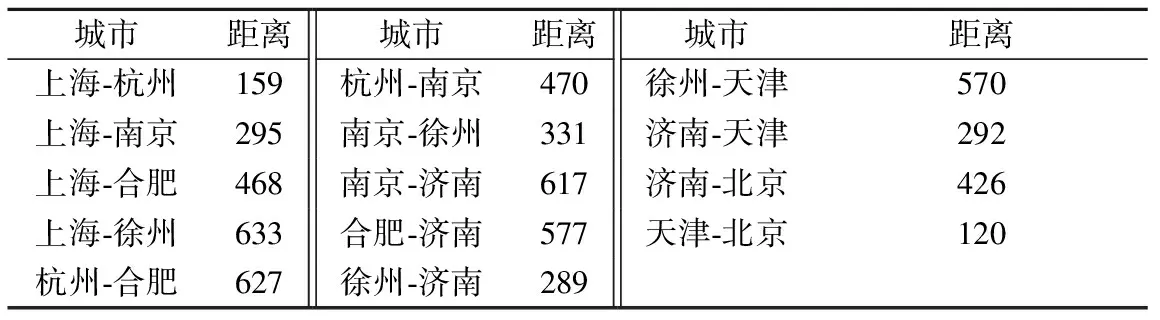
表3 高铁路段距离 km

表4 飞行航段距离 km

表5 节点城市年人均GDP 万元
4.2 模型求解
构建前文提到的城市对上海—北京空铁超级路网,根据表3得空铁换乘城市和高铁换乘城市.由式(5)计算各路段综合阻抗;路网中边的权值等于路段综合阻抗值,结合Floyd算法利用MATLAB编程计算得到任意节点间最短距离矩阵见表6.
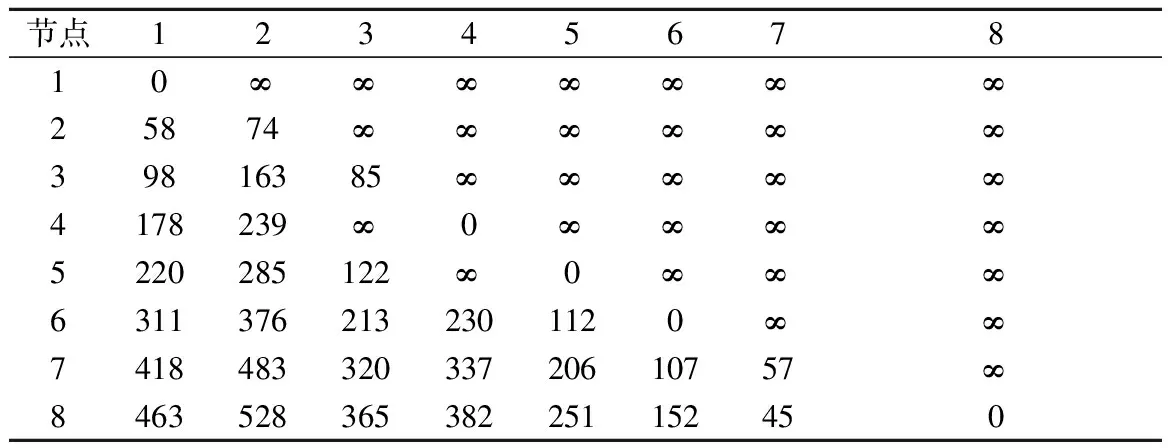
表6 任意节点间最短距离矩阵
现假设上海地区到北京地区旅客出行量M0为100 000人次,根据表6最短距离矩阵,结合交通流分布模型计算得到高铁、航空各路段权重比例和交通量分布见表7~8.
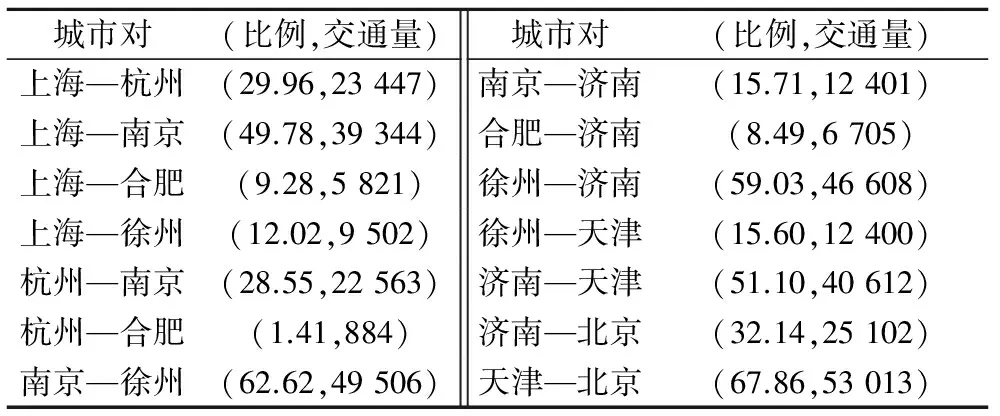
表7 高铁路段权重比例及交通量

表8 航空路段权重比例及交通量
结合表7~8数据可得城市对上海—北京空铁超级路网各路段权重、交通流分布图见图3.
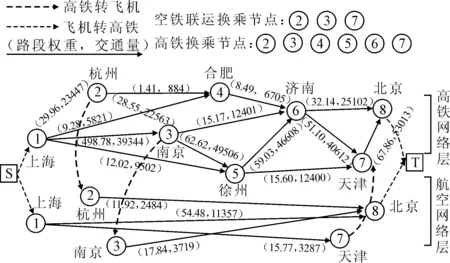
图3 空铁超级路网及各路段参数
表9为路段车次数量和交通量.
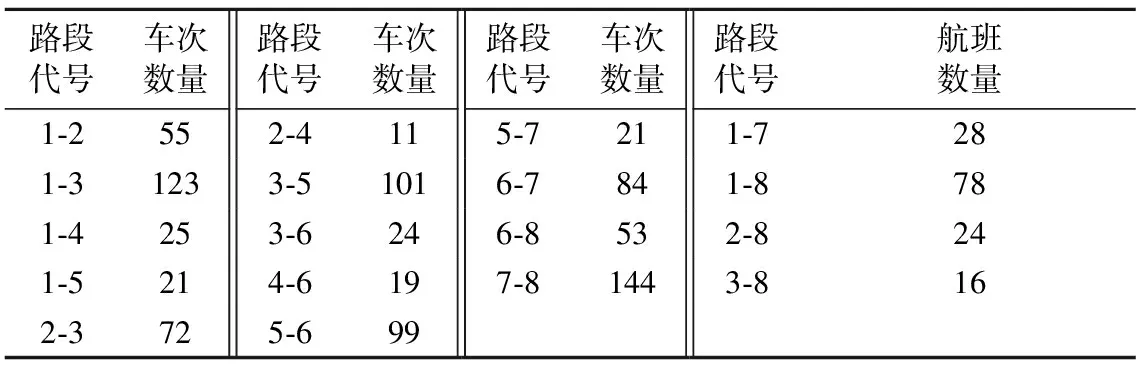
表9 路段车次数量和交通量
由表7~9数据,结合式(8)载运工具运力关系,可得路段车次与路段交通量关系见图4.
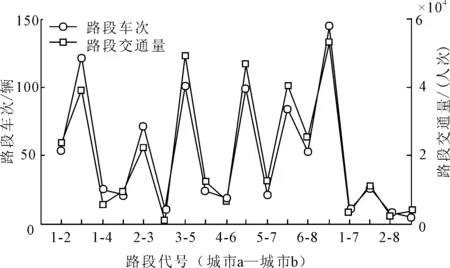
图4 路段车次数量与交通量关系
由图4可知,模型计算得各路段交通量分布与实际投入运力基本吻合.其中路段代号1~3对应上海到南京路段,投放车次比例大于路段交通量分布比例3.1%;路段代号3~5对应南京到徐州路段,交通量分布比例大于投放车次比例2.4%.据此可为有关部门规划交通路网和优化路段运力分布提供决策依据,其余路段分析过程同理.
4.3 交通流分布与票价折扣率μ的关系
飞机票价折扣随市场需求、节假日等因素动态变化,从费用角度影响旅客出行方式的选择,进而影响旅客出行量在航空和高铁的分布比例.从航空公司市场运营角度分析交通流在航空、高铁和空铁联运三种出行方式分布比例随飞机票价折扣率μ的变化关系.由式(2)μ越小,路段阻抗越小,路段分配交通量越大.取μ为0.1~1,结果见图5.
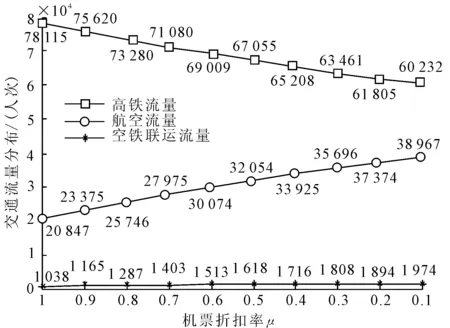
图5 票价折扣率与交通流分布关系
5 结 论
1) 针对城市间空铁旅客出行需求与交通供给运量不匹配的现状,综合考虑旅客出行成本、节点城市人均GDP等因素,建立了基于超级网络的空铁联合交通流分布模型.所提模型能有效得出城市间空铁联合交通流分布与现有供给运力之间的关系,为科学配置空铁运力资源、优化空铁联合交通网络提供理论支撑.
2) 从航空公司市场运营角度分析:旅客出行总量一定时,随飞机票价折扣增大,航空运输和空铁联运分配交通量增加,高铁分配交通量减少.
[1] 中华人民共和国交通运输部.“十三五”现代综合交通运输体系发展规划[Z].北京:中华人民共和国交通运输部,2017.
[2] OKUMURA M, TSUKAI M. Air-rail inter-model network design under hub capacity constraint [J]. Proceedings of the Eastern Asia Society for Transportation Studies,2007(7):180-194.
[3] BEHRENS C, PELS E. Intermodal competition in the London-Paris passenger market: high-speed rail and air transport [J]. Tinbergen Institute Discussion Paper,2012,71(3):278-288.
[4] PAOLA P, JOAQUIN R. Single european sky and single european railway area: a system level analysis of air and rail transportation [J]. Transportation Research Part A: Policy and Practice, Elsevier,2013(1):64-86.
[5] 刘祯根,邓卫.交通分布-交通分配组合模型研究[J].武汉理工大学学报(交通科学与工程版),2006,30(6):1031-1033.
[6] 朱法勇,王正彬.客运专线客流多路径分配模型与算法[J].交通运输工程与信息学报,2016,14(1):76-81.
[7] 王素欣,王雷震.BPR路阻函数的改进研究[J].武汉理工大学学报(交通科学与工程版),2009,33(3):446-449.
[8] 孟梦,邵春福.组合出行模式下多方式交通流分配模型与算法[J].吉林大学学报(工学版),2014,44(1):47-53.
[9] SHEFFI Y. Urban transportation networks: equilibrium analysis with mathematical programming methods [M]. New Jersey: Prentice Hall,1985.
[10] TINBERGEN J. Shaping the world economy: suggestions for an international economic policy[M]. New York:Twentieth Century Fund,1962.
[11] 钟绍林,王修华.北京西站客流集散特征调查[J].铁道运输与经济,2005,27(2):37-39.
[12] 熊伟.运筹学[M].北京:机械工业出版社,2014.
[13] 苏鑫.乘客对飞机票价的定价方法的影响[D].济南:山东大学,2016.
[14] 蔡晓春.城市轨道交通网络客流分配模型与计算方法研究[D].北京交通大学,2011.
[15] 苏娟.城市轨道交通客流分配研究[D].北京交通大学,2009.
The Air-rail Integrated Traffic Flow Distribution Model Based on Super-road Network
DAIFuqingPANGBizhaoYUANJieZHAOYuandi
(CivilAviationUniversityofChina,CollegeofAirTrafficManagement,Tianjin300300,China)
To deal with the increasing serious situation of the vacancy or the short of air-rail transport resources caused by the unmatched volume between passenger’s requirements and the given transport resources in city pairs, the problem of air-rail integrated traffic flow distribution was investigated. The air-rail integrated super-network was constructed by using super-network theory, and the impedance functions of node and path in super-network were established accordingly. Then the weight model and the traffic flow distribution model based on the integrated impedance of the path were designed, and the Floyd algorithm was used to calculate the model. Finally, sample city pairs were selected to be applied to the air-rail super-network model. The results show that the presented model can effectively calculate the volume of air-rail integrated traffic on super-road network. By comparing with the current traffic capacity, the relevant departments can allocate capacity resource reasonably and optimize the distribution of road network capacity. The mismatched problem of traffic supply and actual capacity will also be solved.
air-rail integrated transportation; super-road network; traffic flow distribution; impedance function; floyd algorithm
U113
10.3963/j.issn.2095-3844.2017.05.012
2017-08-10
戴福青(1962—):男,硕士,教授,主要研究领域为空域规划与飞行程序设计
*国家自然科学基金民航联合基金项目(U1533106)、中国民航大学研究生科技创新资助项目(Y17-17)资助
