用洛必达法则巧解函数含参问题

胡意荣

广东省新兴县第一中学 (527400)

用洛必达法则巧解函数含参问题

胡意荣

广东省新兴县第一中学 (527400)

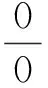
法则一：设函数f(x)、g(x)满足：

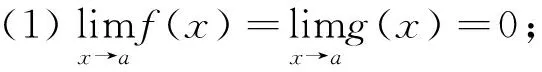
(2)在U°(a)内，f′(x)和g′(x)都存在，且g′(x)≠0；

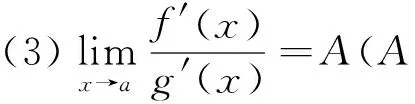
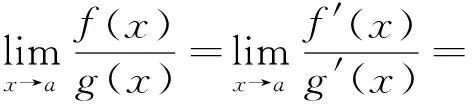
法则二：设函数f(x)、g(x)满足下列条件：

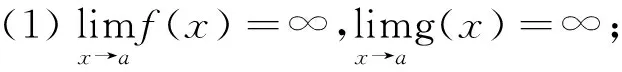
(2)在U°(a)内，f′(x)和g′(x)都存在，且g′(x)≠0；

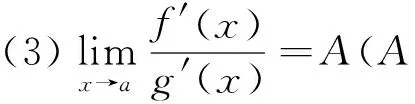
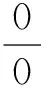
例1 (2016年全国新课标卷2文科第20题)已知函数f(x)=(x+1)lnx-a(x-1).

(Ⅰ)当a=4时，求曲线y=f(x)在(1,f(1))处的切线方程；

(Ⅱ)若当x∈(1,+∞)时，f(x)>0，求a的取值范围.

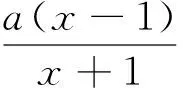
(1)当a≤2，x∈(1,+∞)时，x2+2(1-a)x+1≥x2-2x+1>0，故g′(x)>0,g(x)在(1,+∞)上单调递增，因此g(x)>0；

(2)当a>2时，令g′(x)=0得

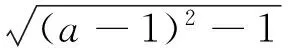
综上，a的取值范围是(-∞,2].

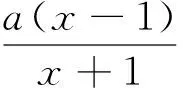
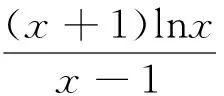
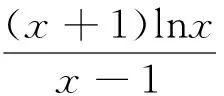
综上，a的取值范围是(-∞,2].

点评：通过对比上述两种解法，不难发现，解法一用的是分类讨论的方法，分类时要注意不重不漏，还要简洁，对解题者的要求较高；而解法二用的是分离参数法，通过分离参数、构造函数，再求导，最后用洛必达法则求极限值，思路清晰，避免了分类讨论的麻烦，可以看出洛必达法则在解决此类问题的优越性.

例2 已知函数f(x)=

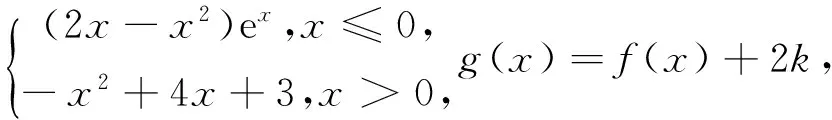
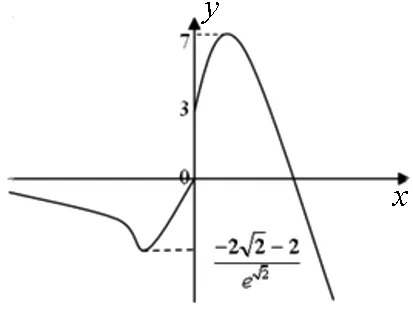
图1

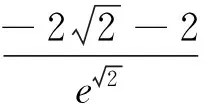
能利用洛必达法则求解参数取值范围的试题还有很多，这类试题也是近些年来高考中的热点.下面给出同类型的几道试题，供读者练习.

1.(2016年高考数学新课标Ⅰ文科第21题)

已知函数f(x)=(x-2)ex+a(x-1)2.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若f(x)有两个零点，求a的取值范围.

2.(2013年高考数学新课标Ⅰ理科第21题)

已知函数f(x)=x2+ax+b，g(x)=ex(cx+d)，若曲线y=f(x)和曲线y=g(x)都过点P(0，2)，且在点P处有相同的切线y=4x+2.

(Ⅰ)求a，b，c，d的值；

(Ⅱ)若x≥-2时，f(x)≤kg(x)，求k的取值范围.

3.(2011年高考数学新课标Ⅰ理科第21题)

(Ⅰ)求a、b的值；

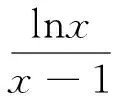
通过上述这些试题，不难看出，在函数问题中求解参数的取值范围时，如果能够分离出参数，把问题转化为恒成立问题，这时就可以利用导数求解所构造函数的最值，如果最值不存在，只有极限值，那么此时往往可以用到洛必达法则来求解，从而避开分类讨论的麻烦，达到提高解题效率的目的.