电导率与硫酸钠百分含量的回归方程探索

蒋小友　于望　吴军

摘要：探索了硫酸钠百分含量在0.0001%～0.5%、0.0001%～0.01%、0.01%～0.5%范围内与电导率之间的线性关系，通过研究两者的关系得出了回归方程，根据两者关系测算了电导率估算溶液的浓度，以方便生产生活。

关键词：回归方程；电导率；硫酸钠；百分含量

中图分类号：TS199

文献标识码：A文章编号：16749944（2017）18012302

1引言

回归分析＼[1～3＼]是用统计学研究变量间的相互关系的一种常用方法，通过最小二乘法＼[4，5＼]找出一条逼近两变量之间的线性关系式，从而通过测量容易的数据推导出不容易测量的数据，方便日常工作的开展。本文通过探索电导率与硫酸钠百分含量的回归方程的关系，得出电导率与浓度的百分含量的关系，通过硫酸钠百分含量与电导率的关系，推广到测出溶液的电导率即可以估算溶液的浓度。

2实验设计

本实验选择了0.0001%～0.5%、0.0001%～0.01%、0.01%～0.5%三个不同的硫酸钠浓度范围，配置硫酸钠溶液并监测其电导率数值，通过统计计算得到回归方程，并用F检验法进行检验＼[6，7＼]。检测仪器：多参数水质分析仪

3结果与讨论

3.1无水硫酸钠百分含量（0.0001%～0.5%）与电导率的关系

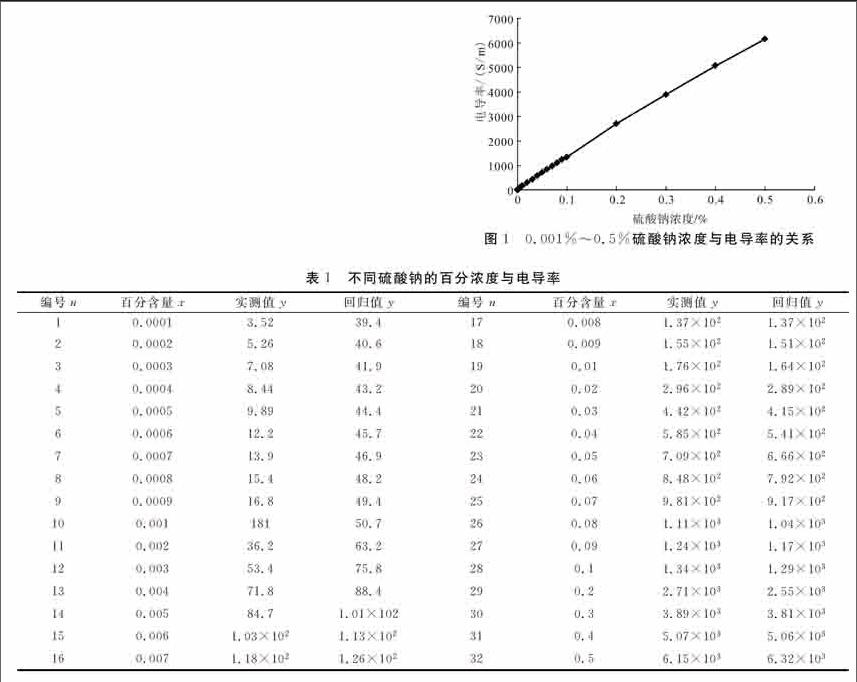
分别配置0.0001%至0.5%共32个不同硫酸钠的溶液并在常温25℃测定溶液的电导率，详见表1。

根据表1的数据绘制线形图如图1。

根据图1及表1，得出硫酸钠百分浓度0.001%～0.5%与电导率的回归方程为：y=38.14+1255980x，其中n=32，A=38.14，B=1255980，计算得到线性相关系数 r=0. 99926777。

3.2無水硫酸钠百分含量（0.0001%～0.01%）与电导率的关系

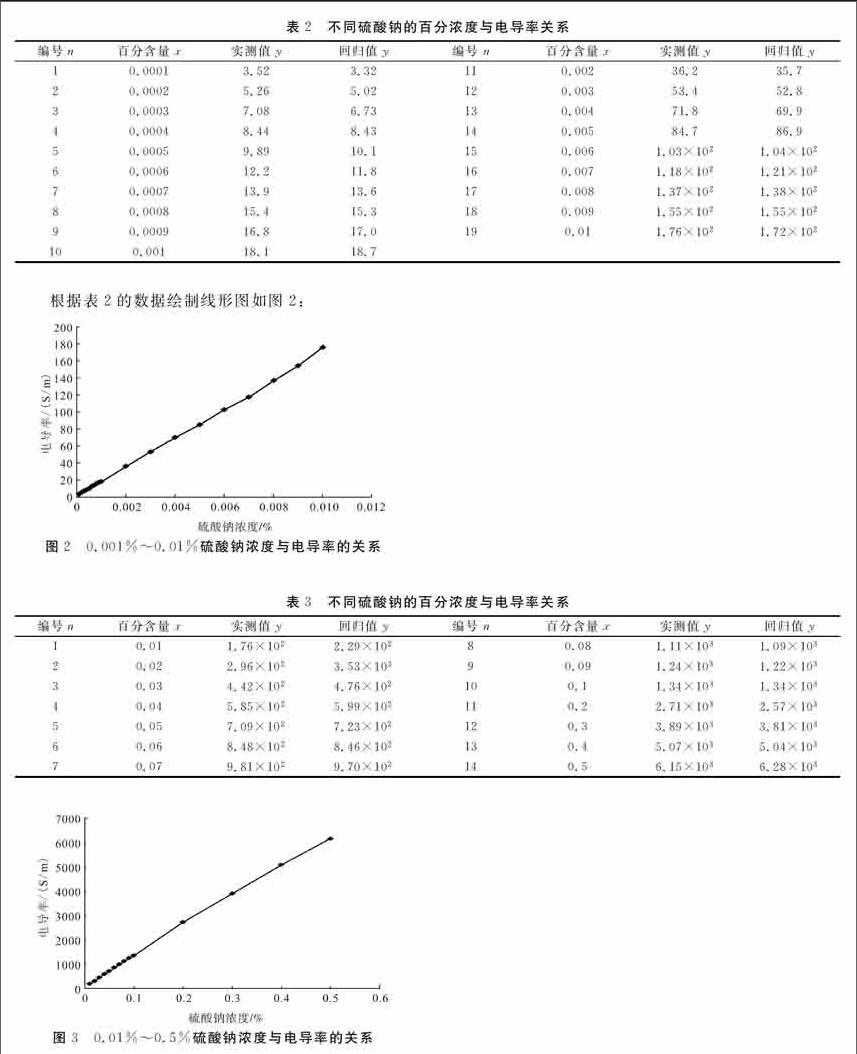
分别配置0.0001%～0.01%共19个不同硫酸钠的溶液并在常温25℃测定溶液的电导率，详见表2。

根据图2及表2，得出硫酸钠百分浓度0.001%～0.01%与电导率的回归方程为：y=1.61+1706064x，其中n=19，A=1.61，B=1706064，计算得到线性相关系数 r=0.99969430。

3.3无水硫酸钠百分含量（0.01%～0.5%）与电导率的关系

分别配置0.01%～0.5%共14个不同硫酸钠的溶液并在常温25℃测定溶液的电导率，详见表3。

根据图3及表3，得出硫酸钠百分浓度0.01%～0.5%与电导率的回归方程为：y=105.84+1234114x，其中n=14，A=105.84，B=1234114，计算得到线性相关系数r=0.99946029。

3.4回归方程的比较分析

（1）25℃下0.0001%～0.01%范围：

n=19，A=1.61，B=1706064，r=0.99969430。

回归方程为：y=1.61+1706064x

计算得到如下一些数据；

∑xy=6.712739，∑x2=6.712739 0.00038785，

∑y2=116242.62。

平均值X=0.00313158，Y=55.036315。

Lxx=0.0002015099，lxy=3.438077，lyy=58691.6965。

U=B·lxy=58655.79，Q=lyy-U=35.9025。

S2=Q/（n-2）=2.1119，s=1.453237，f= n-2=17。

（2）25℃下0.01%～0.5%范围：

n=14，A=105.84，B=1234114，r=0.99946029。

回归方程为： y=105.84+1234114x。计算得到如下一些数据；

∑xy=7345.74，∑x2=0.5785，∑y2=93409227。

平均值X=0.13928571，Y=1824.785714。

Lxx=0.30689287，lxy=3787.40796，lyy=46791426。

U=B·lxy=46740932.936，Q= lyy-U=50493.0636。

S2=Q/（n-2）=4207.7553，s=64.867，f= n-2=12。

（3）用F检验法检验S21和S22有无差异：

F=S2大/S2小=4207.7553/2.1119=1992.4〉〉2.38（F0.05，12，17=2.38）

两回归方程有显著差异，不能合并。

4结论

（1）无水硫酸钠百分含量（0.0001%～0.5%）范围内，回归方程：y=38.14+12559.80x。

（2）无水硫酸钠百分含量（0.0001%～0.01%）范围内，回归方程：y=1.61+17060.64x。

（3）无水硫酸钠百分含量（0.01%～0.5%）范围内，回归方程：y=105.84+12341.14x。

（4）回归方程为：y=1.61+17060.64x和回归方程为： y=105.84+12341.14x有显著差异，不能合并。

（5）通过探索硫酸钠的浓度与电导率的回归方程，可以类比其他溶液测出电导率通过对应的回归方程计算出溶液的浓度，为生产生活提供便利。

参考文献：

[1]

方开泰.实用回归分析＼[M＼]. 北京：科学出版社 ，1988.endprint

＼[2＼]王麗华. 回归分析在环境监测中的应用＼[J＼]. 包钢科技，2006（S1）.

＼[3＼]鲁铁定，陶本藻，周世健. 一元整体线性回归模型解算＼[J＼]. 西安科技大学学报，2009（2）.

＼[4＼]彭放，吴国平，方敏.经典回归直线的非唯一性研究＼[J＼]. 数学的实践与认识，2001（4）.

＼[5＼]梁家惠. 用最小二乘法进行直线拟合的讨论＼[J＼]. 工科物理，1995（3）.

＼[6＼]高峰，郭云.正态总体均值的F检验法＼[J＼].淮阴工学院学报，14（5）：6～7.

＼[7＼]李玉明，何文章； 王海军.F检验法临界值的计算＼[J＼]. 有色金属，1992（4）：39～41.

Regression Equation of Conductivity and Percentage of Sodium Sulfate

Jiang Xiaoyou， Yu Wang， Wu Jun

（Jieyang City Surface Treatment Ecological Industrial Park Co.， Ltd.， Jieyang 522000， China）

Abstract： This paper mainly explored the linear relationship between the percentages of sodium sulfate in the range of 0.0001%-0.5%， 0.0001%-0.01%， 0.01%-0.5% and conductivity. Through the exploration of the regression equation， the relationship between the two was estimated. The concentration of the solution was estimated according to conductivity estimation， which is convenient in production and life.

Key words： regression equation； conductivity； sodium sulfate； percentageendprint