某上承式拱桥减震控制理论分析

■陈炜华

(漳州市顺通路桥建设有限公司，漳州 363000)

某上承式拱桥减震控制理论分析

■陈炜华

(漳州市顺通路桥建设有限公司，漳州 363000)

上承式拱桥是一种常见桥型，其抗震性能较低，难以设计成延性抗震结构。本文尝试将阻尼器应用到拱桥的减震控制中，运用Midas软件进行有限元分析，通过比较分析以讨论较为合理的减震控制方案。

上承式拱桥 阻尼器 减震控制

1 引言

拱桥由于主拱圈轴压比较大，横向刚度较低，延性较低，难以设计成延性抗震结构。在地震作用下往往受到不可逆的破坏，采取适当的减震措施是控制拱桥地震响应一种经济有效的途径。本文试图在拱桥模型中加入阻尼器，以讨论阻尼器对拱桥减震控制中的适应性以及减震器的优化布置。

2 有限元模型及阻尼器参数

某上承式拱桥为单孔双曲拱桥，主拱圈为等截面无铰拱，净跨径为30.00m，净矢高为5.00m，净矢跨比F0/L0=1/6。桥面净宽约为7.0m，布置为1.2m人行道+4.6m车行道+1.2m人行道。拱圈厚度为50cm，由5拱4波组成。主拱圈两侧各3个腹拱，边腹拱为三铰拱，腹拱圈为预制混凝土试块拼装。

本文所采用的阻尼器是摩擦耗能阻尼器，由模管、钢棒、内圆筒和外圆筒组成，钢棒与模管紧密套合，其中钢棒的直径比模管的内径稍微大一点，以保证当钢棒滑移时在模管紧固力作用下产生恒定的摩擦力。这种摩擦耗能阻尼器与支撑构建串联使用时，在外荷载作用下的反应呈现理想弹塑性。经反复试算，摩擦耗能阻尼器支撑的参数为：刚度为1000kN/mm，屈服强度为7000kN。

图1 拱桥有限元模型

3 计算结果及分析

3.1 自振特性

经计算，桥梁的前3阶振型如表1所示。

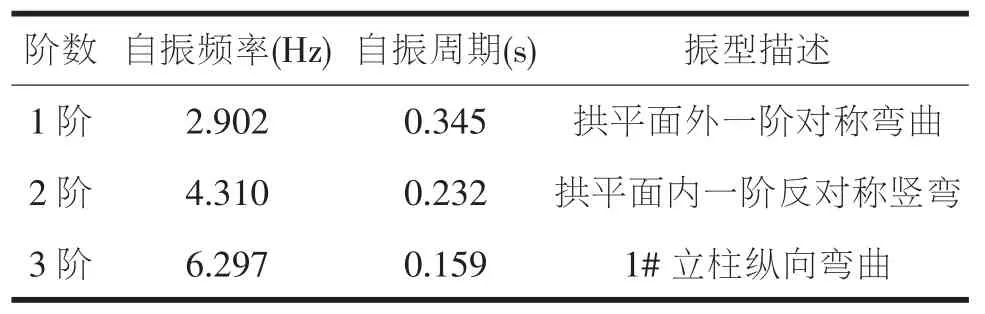
表1 前3阶振型及其描述

3.2 未设置阻尼器的地震响应

此次计算选用两条地震波 (EI-Centro波、Hollywood Storage波)作为时程分析的地震震动输入，为充分考虑阻尼器的作用，将上述地震波的峰值加速度均调整为0.4g。每个地震波输入时分别考虑两种工况：工况一仅考虑地震动顺桥向和横桥向输入，不考虑竖向地震波速；工况二为顺桥向、横桥向和竖向三个方向输入。拱顶及1/4拱截面的位移最大值如表2、表3所示。

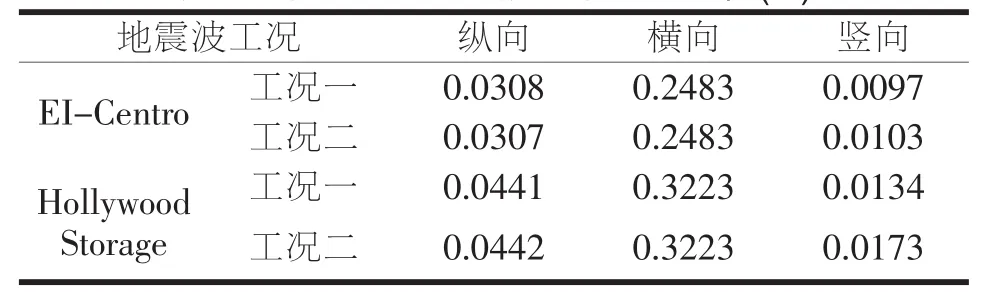
表2 未设置阻尼器拱顶最大位移值(m)

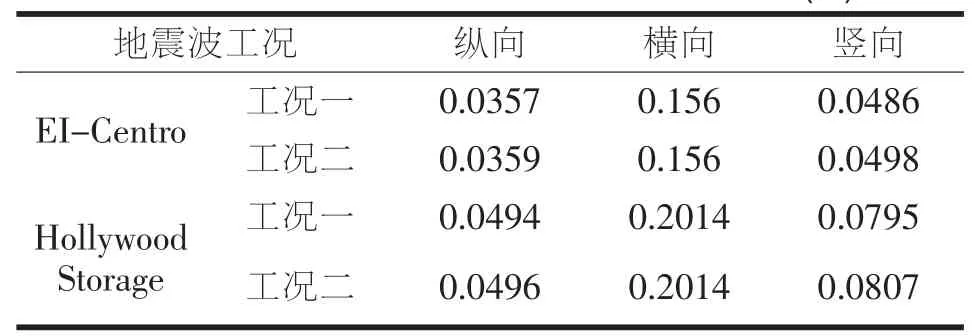
表3 未设置阻尼器1/4拱截面位移最大值(m)

3.3 阻尼器布置方案及设置阻尼器的地震响应

由表1～表3可知，该拱桥的面外刚度较低，横向位移响应较大。此次理论计算从拱脚至拱顶的两拱肋间的横撑间逐次对称增加阻尼器的数量(2，4，……，10)，分析对比阻尼器的优化布置方案及减震效果。

对设置不同数量阻尼器的计算模型进行地震响应分析，引入减震率μ，定义为：

其中：φa、φb分别为设置阻尼器前后的响应值。

拱顶位置及拱脚面外弯矩的减震效果见表4、表5。

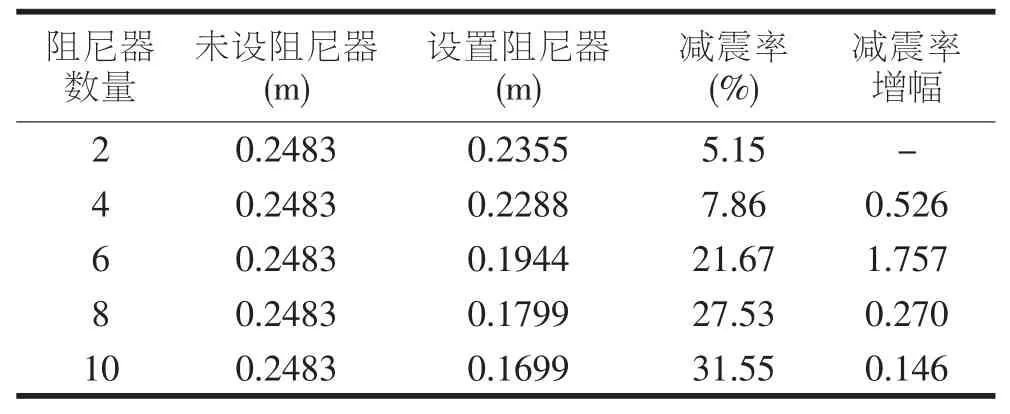
表4 拱顶横向位移减震效果

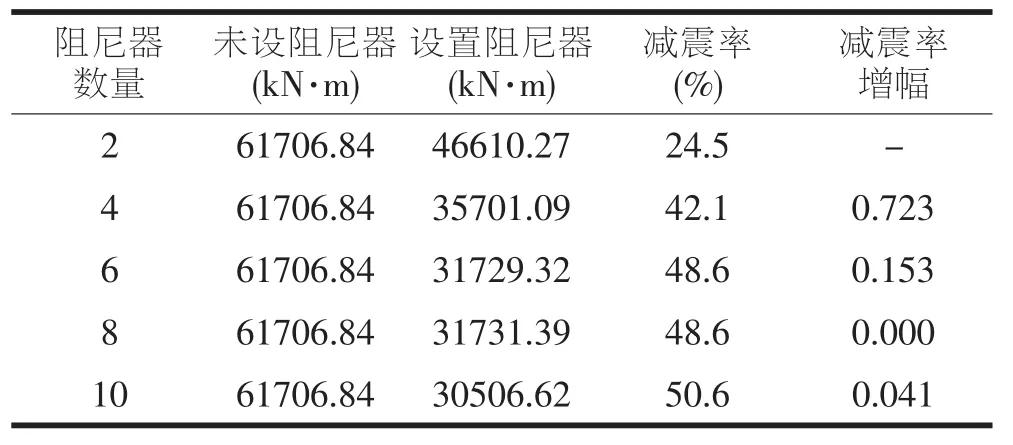
表5 拱脚面外弯矩减震效果

由表4、表5可知：

(1)拱顶横向位移减震率随着阻尼器数量的增加而增加，当其阻尼器数量由4个增加为6个时，减震率增幅最大，说明此时增加的阻尼器对拱顶位移控制效果最好；阻尼器数量由6个增加10个时，减震率增幅较平缓，说明在此阶段增加阻尼器数量对位移控制的影响相对较小。

(2)拱脚面外弯矩减震率随着阻尼器数量的增加而增加，当其阻尼器数量由2个增加为4个时，减震率增幅最大，说明靠近拱脚设置阻尼器对拱脚面外弯矩的控制效果最好；阻尼器数量由6个增加10个时，减震率增幅较平缓，说明在此阶段增加阻尼器数量对拱脚面外弯矩的影响相对较小。

4 结论

通过以上的比较研究可以看出：设置阻尼器能够有效减少拱桥的地震响应，在拱桥减震控制中具有较好的应用前景。在大震中，阻尼器通过摩擦耗能以消耗地震输入的能量，不禁可以减少拱顶的横向位移响应，而且可以较大程度的减小拱脚面外弯矩。阻尼器布设位置和数量对拱桥的减震效果具有较大影响，在采用时应对其进行优化，从而达到经济、安全的效果。

[1]李正英，等.粘滞阻尼器拱桥结构减震控制研究[J].振动与冲击，2007，26(1).

[2]范立础.桥梁延性抗震设计[M].北京：人民交通出版社，2001.

[3]周云.摩擦耗能阻尼减震结构设计[M].武汉：武汉理工大学出版社，2006.