基于遗传算法的加压滴灌系统管网优化设计

郭 铭

(辽宁江河水利水电新技术设计研究院，辽宁 沈阳 110003)

基于遗传算法的加压滴灌系统管网优化设计

郭 铭

(辽宁江河水利水电新技术设计研究院，辽宁 沈阳 110003)

滴灌系统干管设计是否合理，直接影响滴灌系统投资及运行费用，本文以滴灌系统年费用最低为目标，建立了滴灌系统管网优化模型，采用遗传算法对模型进行求解。应用结果表明：该模型及算法能够快速、准确地计算出管网优化方案及水泵优化扬程，适合滴灌系统管网的优化设计。

滴灌；管网优化；优化模型；遗传算法

加压滴灌系统的干管造价约占滴灌系统总造价的50%左右，直接影响滴灌系统投资，管网的水头损失也直接影响了滴灌系统的首部压力及其能耗。因此，进行滴灌系统输水管网优化设计研究，减少工程造价，降低系统运行费用，对滴灌工程经济效益的发挥具有重要意义。国内外学者对灌溉输水管网的优化设计进行了一些研究，并取得了一定成果，优化计算方法也从线性规划[1]、非线性规划[2]、动态规划[3]等传统方法，发展为采用遗传算法[4]、神经网络算法[5]等智能算法，解决了传统方法计算量大、优化精度低等缺点，但这些方法仍存在易陷入局部最优解等缺陷。本文在保证滴灌系统流量及压力的前提下，建立以滴灌系统年费用最低为目标的优化模型，采用遗传算法进行求解，得到了管网优化结果。

1 管网优化数学模型的建立及求解方法

1.1 目标函数

当管网首部压力未定时，管网优化设计既要考虑降低工程造价，又要考虑降低运行费用。减少干管管径可以减少工程投资，但会增加管网水头损失，增加系统运行费用；增加干管管径可以减少水头损失，但会增加工程造价。以管段管径和管网首部压力为决策变量，以滴灌系统年费用最低为目标，寻找工程造价和运行费用的平衡点，建立如下数学模型：

(1)

式中：F为管网年费用，元/a；t为工程使用年限，a；P为年维修费率，%；r为年利率，%；N为管网管段数；M为标准管径数,种；Cij为第i管段第j种管径的单价，元/m；Lij为第i管段第j种管径的长度，m；E为电价，元/(kW·h)；T为水泵年工作小时数，h；Q为水泵流量，m3/h；H为水泵扬程，m；η为水泵效率。

1.2 约束条件

各支管入口节点的实际工作压力不应低于该节点所需工作压力。

(2)

(3)

式中：Zb为水源水位，m；h为首部工程水头损失，m；I(k)为首部工程到第k支管入口节点所经过的干管管段数；Zk为k节点地面高程，m；Hz为支管入口所需压力，m;Jij为第i管段第j种管径的水力坡度，m/m;a为局部水头损失加大系数；f、m、b为水头损失计算系数；Qi为第i管段流量，m3/h；di为第i管段管道内径，mm。

管道实际工作压力不应大于管道承压力。

(4)

式中：Hc为管道承压力，m。

非负约束：

di≥0，H≥0

(5)

1.3 模型求解方法

采用遗传算法对模型进行求解。遗传算法是借鉴自然界生物遗传和变异而开发的一种全局优化概率搜索算法。它将问题的优化过程表示成基因的进化过程，将随机生成的初始解，通过选择、交叉、变异等一系列操作，最终得到问题的优化解。

(1)适应度函数构造。以目标函数构造适应度函数，将目标函数最小化问题转化为最大化问题。

(2)编码。模型的优化变量为di和H，di采用整数编码方式，H采用实数编码方式。

(3)遗传操作。首先对群体中的个体进行适应度评价，选择最好的个体作为父个体；其次是在交叉概率Pc控制下，将选择的父个体随机配对，并进行交叉运算，产生下一代个体；之后在变异概率Pm控制下，随机选择基因及基因位，并对其进行随机变异。

(4)如此反复，最终得到问题的优化解。

2 应用算例

以文献[6]中应用算例为例进行计算，管网布置如图1所示，管网采用聚乙烯管材，管道单价见表1，支管入口地面高程见表2，微灌系统分为3个轮灌组运行，轮灌组序号分别为1、4、7，2、5、8和3、6、9。模型中参数取值如下：r=7%，t=15 a，P=3%，E=0.6元/(kW·h)，T=370.8 h，Q=33 m3/h，η=0.6，Zb=11.4 m，a=1.05，h=7 m，Hc=0.8 MPa，支管入口压力水头为12.6 m，支管流量为11 m3/h，f=0.948×105，m=1.77，b=4.77。

图1 管网布置示意图

管径/mm506580100单价/(元·m-1)5.548.8011.8016.40

表2 支管入口地面高程

遗传参数设置：初始种群Z=50，交叉概率Pc=0.9，变异概率Pm=0.05，进化代数为100。将有关数据输入模型进行计算，得到管网优化结果见表3、表4。

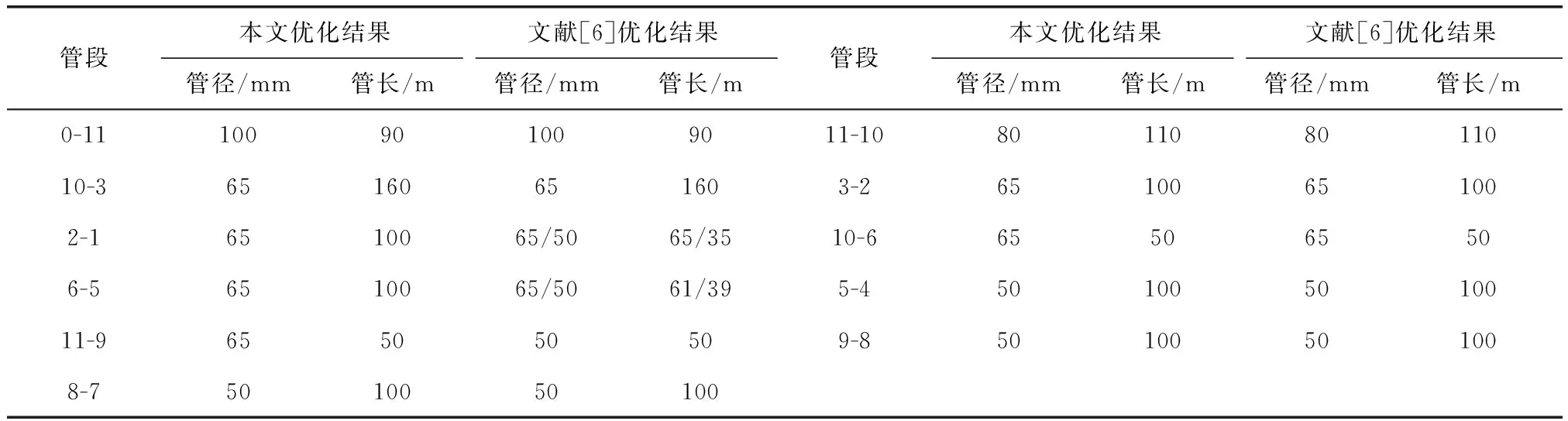
表3 管径管长优化结果

由表3可知，本文管径及管长的优化结果与文献[6]中优化结果基本一致，为施工方便，本文在固定管段间采用一种管径，以便减少安装及连接管件的费用。

由表4可知，本文计算的水泵扬程为36.14 m、滴灌系统年运行费用为2513.35元/a，与文献[6]中的水泵扬程为36.27 m、滴灌系统年运行费用为2467.86元/a的计算结果相似，但本文模型及算法简单易用，优化变量少，采用遗传进行求解精度及效率高，能够满足滴灌系统管网设计要求。

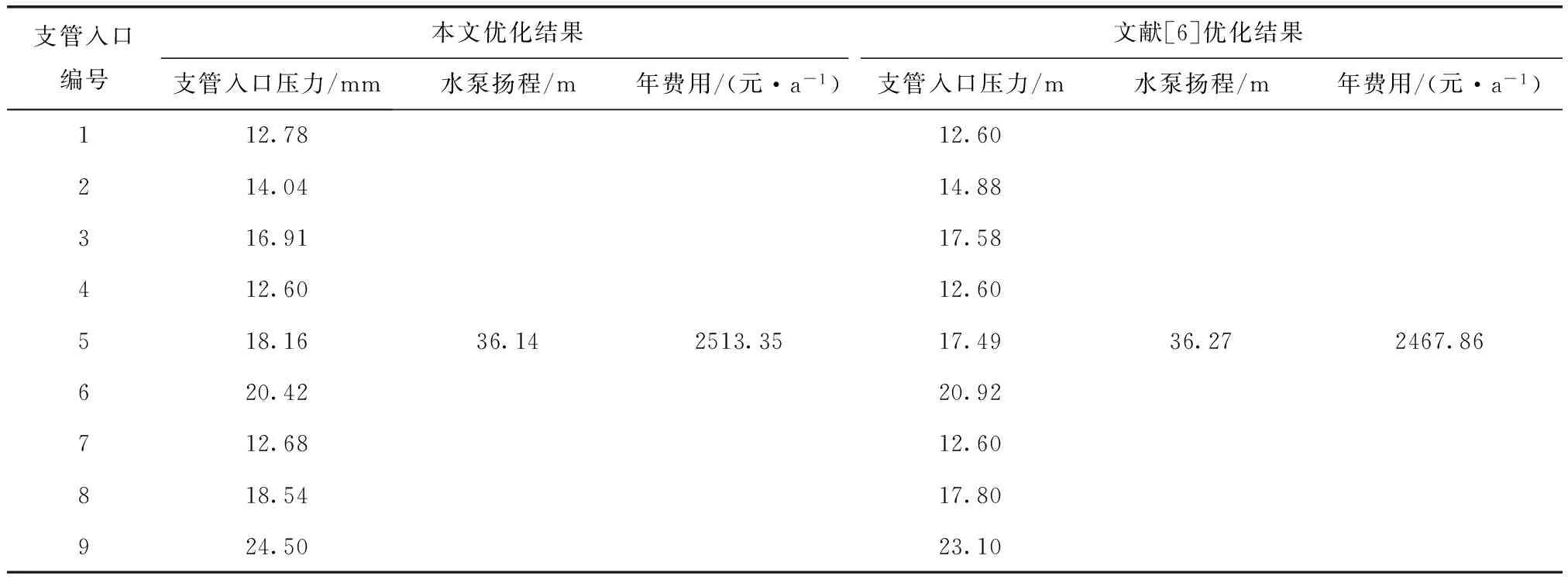
表4 节点压力及水泵扬程优化结果

3 结 论

以滴灌系统年费用最低为目标，建立了滴灌系统管网优化模型，采用遗传算法对模型求解，具有收敛速度快、算法稳定性高等优点，通过应用算例对模型进行了验证，并与以往研究结果进行比较，证明了该模型及算法能够快速、准确地计算出管网优化方案及水泵优化扬程。模型优化变量少，算法简单易用，适合滴灌系统管网的优化设计。

[1] Brendanl B,George K. Network linear programming as pipe network hydraulic analysis tool[J].Journal of Hydraulic Engineering, 1997,123(6):549-559.

[2] Cunham D,Sousa J.Water distribution network design optimization: simulated annealing approach[J].Journal of Water Resources Planning and Management,1999,125(4):215-221.

[3] 魏永曜，王雪珍．树状输配水管网的优化设计[J]．水利学报，1992，23(5)：9-18.

[4] 马孝义，范兴业，赵文举，等．基于整数编码遗传算法的树状灌溉管网优化设计方法[J]．水利学报，2008，39(3)：373-378.

[5] 周荣敏，买文宁，雷延峰，等．自压式树状管网神经网络优化设计[J]．水利学报，2002，33(2)：66-70.

[6] 白丹．微灌管网系统优化设计[J]．农业机械学报，1997，28(4)：63-68.

Optimal design of pipe network in pressurized drip irrigation system based on genetic algorithm

GUO Ming

(LiaoningRiverWaterConservancyandHydropowerDesignandResearchInstituteofNewTechnology,Shenyang110003,China)

The design of main pipe in drip irrigation system is reasonable or not affects the investment and operation cost of drip irrigation system directly, This paper regards the irrigation system cost minimum as the goal, establishes the pipe network optimization model of drip irrigation system and uses genetic algorithm to solve the model. The application results show that the model and algorithm can calculate the optimal scheme of the pipe network and the optimal pump head quickly and accurately, which is suitable for the optimal design of the pipe network of drip irrigation system.

drip irrigation; pipe network optimization; optimization model; genetic algorithm

S274.2

A

2096-0506(2017)09-0010-04

国家科技支撑计划(2014BAD12B04)；辽宁省农业科技创新团队项目(2014212003)

郭 铭(1983-)，男，辽宁鞍山人，工程师，主要从事灌溉排水理论与技术研究。E-mail:guoming27@163.com。