遗传优化核极限学习机的数据分类算法*

何 敏, 刘建伟, 胡久松

(湖南大学 电气与信息工程学院,湖南 长沙 410082)

遗传优化核极限学习机的数据分类算法*

何 敏, 刘建伟, 胡久松

(湖南大学电气与信息工程学院,湖南长沙410082)

为了提高核极限学习机(KELM)数据分类的精度,提出了一种结合K折交叉验证(K-CV)与遗传算法(GA)的KELM分类器参数优化方法(GA-KELM),将CV训练所得多个模型的平均精度作为GA的适应度评价函数,为KELM的参数优化提供评价标准,用获得GA优化最优参数的KELM算法进行数据分类。利用UCI中数据集进行仿真,实验结果表明：所提方法在整体性能上优于GA结合支持向量机法(GA-SVM)和GA结合反向传播(GA-BP)算法,具有更高的分类精度。

核极限学习机； 遗传优化； 交叉验证； 参数优化； 分类精度

0 引 言

分类问题是数据挖掘[1,2]领域中的重要研究内容,目前已有的数据分类方法如神经网络(neural network,NN)法[2,3]、贝叶斯网络方法[2,4]、支持向量机(support vector machine,SVM)法[2,5]、核极限学习机(kernel-based extreme learning machine,KELM)法等。其中KELM由于网络结构简单,学习速度快,泛化能力强等优点,在数据分类中具有很大的优势。

KELM[6]是Huang Guangbin在其所提出的ELM算法之上结合核函数所提出的改进算法。ELM在保证网络具有良好泛化性能的同时,极大提高了前向神经网络学习速度,并避免了以反向传播(back propagation,BP)神经网络为代表的梯度下降训练方法的许多问题,如容易陷入局部值、迭代量大等。KELM不仅有ELM算法的许多优势,同时结合了核函数,对线性不可分的模式进行非线性映射到高维特征空间从而实现线性可分,进一步提高了判断的准确率。然而,由于核函数的存在,导致了这种算法对参数设置具有敏感性。本文拟采用交叉验证(cross validation,CV)和遗传算法(genetic algorithm,GA)的方法对KELM参数进行优化,而后将优化参数应用到KELM算法中,并用KELM算法进行数据分类,同GA-BP[7]和GA-SVM[8]算法相比,具有更高的分类精度。

1 基本原理

1.1 GA原理

GA以自然选择和遗传理论为基础,将生物进化过程中适者生存规则与种群内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法[9,10],将问题参数编码为染色体,再利用迭代的方式进行选择,交叉以及变异等运算交换种群中染色体的信息,从而使种群代代进化到搜索空间中越来越好的区域,直至达到最优解点[11]。其主要步骤如下：1)确定寻优参数进行编码,编码时首先设置编码长度；2)随机产生初始种群；3)计算种群中每个个体的适应度函数值；4)形成匹配集。根据种群中每个染色体的适应度函数值,采用一定的方法,从种群中选出适应值较大的染色体；5)按某种复制规则进行繁殖，繁殖主要有2种方法：交叉和变异；6)若遗传代数达到给定的允许值或其他收敛条件满足时停止遗传,否则，返回步骤(3)。

1.2 KELM原理

KELM是一种单隐层前向神经网络(SLFN)的训练算法,SLFN模型可表示为[12]

f(x)=h(x)β=Hβ

(1)

式中x为样本输入；f(x)为神经网络的输出,在分类过程中其为类别向量；h(x),H为隐含层特征映射矩阵；β为隐含层输出层连接权重。在KELM算法中有

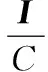
(2)

式中T为训练样本的类标志向量组成的矩阵；C为正规化系数；I为单位矩阵。

在隐含层特征映射h(x)未知的情况下,可将KELM的核矩阵定义如下[13]

ΩELM=HHT:ΩELMi,j=h(xi)h(xj)=K(xi,xj)

(3)

则可将式(1)变换为

(4)

使用径向基函数(RBF)为核函数,即

(5)

2 GA优化KELM原理

2.1 GA优化KELM参数方法

由式(4)和式(5)可以得到正规化系数C和核函数参数s是需要设定的参数,是影响KELM分类的重要因素。因此,对KELM参数优化,即是对正规化系数C和核函数参数s的优化。将KELM分类精度记为acc(C,s),参数C和s上界分别为a和b,下界均为0,则KELM参数优化模型为

maxacc(C,s)

st:C∈[0,a]

st:s∈[0,b]

(6)

即在给定区间内寻找一组C和s,使得KELM在所给数据上分类精度达到最大。本文采用7折交叉验证[14,15](7-CV),所得7个分类模型的平均精度作为遗传算法中个体的适应度。其中,交叉验证精度可用下式表达

(7)

图1 7折交叉验证与GA结合优化参数算法流程

2.2 GA优化KELM数据分类算法

本文采用7折交叉验证和GA优化算法对核极限学习机参数进行优化,从而得到优化参数C和s,而后将优化参数应用到KELM算法中进行数据分类。具体算法流程如下:

1)将样本按4︰1分为训练样本和测试样本,训练样本用于训练参数,测试样本用于分类精度测试；

2)对训练样本和测试样本进行归一化处理；

3)确定遗传代数、种群数量、交叉概率、变异概率以及参数C和s的变化范围；

4)采用7折交叉验证,按式(7)计算交叉验证精度acc作为遗传个体适应度,对KELM分类参数进行评价；

5)对种群进行选择、交叉、变异,得到新的种群,如果满足条件,则得到最大的分类准确率,否则,返回步骤(4)；

6)输出最优参数和最优模型,并用测试样本对获得最优参数的KELM算法进行分类精度测试。

3 实验设计与实验结果分析

3.1 实验设计

为验证本文所提方法的有效性,将GA-KELM,GA-SVM,GA-BP3种算法分别用于数据分类预测。其中,实验数据采用UCI标准数据集中的Segment,Iris,Diabetes数据集,按4︰1分为训练数据和测试数据。

实验中,首先对实验数据进行归一化处理,采用7折交叉验证与GA结合用于KELM参数优化,遗传代数为50,种群规模为30,交叉概率0.4,变异概率0.01,参数C范围[0,1000],参数s范围[0,2],适应度函数按式(7)计算,具体算法流程按照3.2所述。

3.2 实验结果分析

取20次预测实验的平均值作为数据分类精度,图2给出了3种算法在数据集上分类精度的对比,表1给出了3种算法在各数据下分类耗时对比。由图1可以看出,3种算法均可以进行数据分类,但GA-KELM的分类精度最高,GA-SVM次之,GA-BP较差。

图2 3种算法在数据集上分类精度对比

由表1可以看出在同样的数据样本下,3种算法的耗时各不相同,GA-KELM最少,GA-SVM次之,GA-BP最多。综上,GA-KELM是一种更加有效的数据分类算法。

表1 3种算法在各数据集上耗时对比

4 结束语

针对KELM数据分类精度易受正规化系数C和核函数参数s影响问题,提出了一种结合K折交叉验证(K-CV)与GA结合的KELM分类参数优化方法：将交叉验证所得多个模型的平均精度作为GA的适应度函数值,为KELM的参数优化提供评价标准,而后将GA优化所得参数应用到KELM算法中用于数据分类。为验证所提算法的有效性,文中将GA-KELM,GA-SVM,GA-BP 3种算法用来对UCI中Segment,Iris,Diabetes 3个数据集数据进行分类预测,并对 3种算法的分类精度和耗时进行了对比,结果表明,本文所提算法在分类精度和耗时上均优于其他2种算法,说明算法可靠有效。

[1] Han J,Kamber M.数据挖掘概念与技术[M].2版.范 明,孟小峰,译.北京:机械工业出版社,2007.

[2] 钱晓东. 数据挖掘中分类方法综述[J]. 图书情报工作,2007，3:68-71.

[3] 龚雪飞,徐 景,孙寿通,等.PSO-BP神经网络在多元有害气体检测中的应用[J].传感器与微系统,2015,34(2):154-156.

[4] Khanteymoori A R,Homayounpour M M,Menhaj M B.Advances in computer science and engineering[M].Berlin Heidelberg:Springer,2009:25-32.

[5] 陈中杰,蒋 刚,蔡 勇.基于SVM一对一多分类算法的二次细分法研究[J].传感器与微系统,2013,32(4):44-47.

[6] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine：Theory and applicant[J].Neurocomputing,2006,70(1/2/3)：489-501.

[7] 杨 卿,郭 斌,罗 哉,等.遗传优化神经网络在气密性检测中的应用[J].传感器与微系统,2011,30(2):132-134.

[8] 伊 鑫,李 辉,冯剑川.基于遗传优化SVM的通信信号的分类[J].信息化研究,2010,36(3):49-51.

[9] 雷英杰,张善文,李续武,等．Matlab 遗传算法工具箱及应用[M]．西安：西安电子科技大学出版社,2005.

[10] 周 明,孙树栋．遗传算法原理及应用[M]． 北京：国防工业出版社,1999.

[11] 唐朝晖,王 迅.基于遗传算法的大功率电机效率的在线测量[J].传感器与微系统,2012,31(9):132-135.

[12] Huang Guangbin,Zhou Hongming,Ding Xiaojian.Extreme lear-ning machine for regression and multiclass classification[J].IEEE Transaction on Systems Man and Cybemetics,2012,42(2):513-529.

[13] Huang Guangbin,Wang Dianhui,Lan Yuan,et al.Extreme lear-ning machines:A survey[J].International Journal of Machine Learning and Cybernetics,2011,2(2):107-128.

[14] Alippi C,Roveri M.Virtual k-fold cross validation:An effective method for accuracy assessment[C]∥The International Joint Conference on Neural Networks,2010:1-6.

[15] Chalimourda A,Scholkopf B,Smola A.Experimental optimal V in support vector regression for different noise models and parameter settings[J].Neural Networks,2004,17(1):127-141.

Geneticoptimizationkernel-basedextremelearningmachinedataclassificationalgorithm*

HE Min, LIU Jian-wei, HU Jiu-song

(CollegeofElectricalandInformationEngineering,HunanUniversity,Changsha410082,China)

In order to improve precision of data classification of kernel-based extreme learning machine(KELM),propose KELM classification parameter optimization method,GA-KELM,which combinesK-fold cross-validation(K-CV) and genetic algorithms(GA),the average precision of multiple models of resulting of CV training as GA fitness evaluation function value,provide evaluation criteria for parameter optimization of KELM ,and then the KELM algorithm is used to get the optimization parameters of GA for data classification.Using UCI dataset for simulation,results show that the proposed method is superior to GA-SVM and GA-BP algorithm on the overall performance,with a higher classification precision.

kernel-based extreme learning machine(KELM); genetic optimization; cross validation; parameter optimization; classification precision

10.13873/J.1000—9787(2017)10—0141—03

2016—09—26

中央国有资本经营预算项目(财企2013470号)；中央高校基本科研项目(2014—004)；国家自然科学基金资助项目(61172089)；湖南省科技计划资助项目(2014WK3001)；中国博士后科学基金资助项目(2014M562100)

TN 911.7

A

1000—9787(2017)10—0141—03

何 敏(1977-),女,博士,助理教授,主要研究方向为视觉特征检测、复杂系统优化控制。