基于指数阈值迭代法的高精度地震数据重建
2017-11-01张华,杨会,刁塑,刘军
张 华, 杨 会, 刁 塑, 刘 军
(东华理工大学省部共建核资源与环境国家重点实验室培育基地,江西 南昌 330013)
基于指数阈值迭代法的高精度地震数据重建
张 华, 杨 会, 刁 塑, 刘 军
(东华理工大学省部共建核资源与环境国家重点实验室培育基地,江西 南昌 330013)
地震勘探数据采集中,地震道缺失是不可能避免的现象。为了满足后续处理和解释的要求,缺失道数据重建是地震勘探数据处理中必不可少的预处理环节。为此,提出一种基于指数阈值迭代法的高精度重建方法进行叠前重建。引入能够刻画地震数据局部化特征的多尺度多方向二维曲波变换,采用阈值迭代法进行数据重建,并在迭代过程中采用软阈值算子去除由欠采样所引起的随机噪声干扰。同时在重建过程中针对传统阈值参数收敛速度较慢的缺点,提出了一种新的指数阈值参数公式,降低计算迭代次数和提高重建精度。理论数据的模拟表明,该方法重建效果显著,计算速度较快,应用于实际地震勘探资料,获得较好的重建效果。
曲波变换;软阈值;数据重建;阈值迭代法
张华, 杨会,刁塑,等.2017. 基于指数阈值迭代法的高精度地震数据重建[J].东华理工大学学报:自然科学版,40(3):253-260.
Zhang Hua, Yang Hui, Diao Su, et al.2017. High precision reconstruction of seismic data based on exponential threshold iteration method[J].Journal of East China University of Technology (Natural Science), 40(3):253-260.
在地震勘探中,受复杂地质条件和采集环境的影响,例如障碍物、湖泊、禁采区以及人工干扰等,导致所采集到地震数据通常不完整、不规则,出现大量的地震缺失道,难以满足后续处理以及资料解释的要求,降低了地震勘探的分辨率(高建军等,2011;陈晓等,2016;黄光南等,2016)。同时由于项目勘探成本的限制,不可能再到野外对缺失地震道进行补充采集和加密。但是在地下介质为连续性和可预测性的基础上,在室内可以采用高效率高精度的数据重建方法重建出缺失的地震道,满足高分辨率地震勘探的要求。另外一方面,这种高效率高精度的重建方法也可以主动指导复杂地区的地震数据采集,保证整个地震勘探的施工效率以及节省一定的野外成本。
目前,基于曲波变换的数据重建方法研究较多(徐卫等,2016;张华等,2013;Zhang et al., 2015),并且也发展到了三维数据重建,所采用的算法主要有阈值迭代法(Herrmann et al., 2008)、凸集投影算法(Zhang et al., 2013)及谱投影梯度法等(Berg et al., 2008)。一般来讲,该类重建方法参数设置简单且不需要地下速度结构信息,计算效率较快,精度高。而对于阈值迭代算法,参数设置尤为简单,并且重建效果也较为显著,然而由于采用了曲波变换,运算速度仍然较慢,从而使得该方法得不到广泛的应用。实际上,该方法运算速度快慢的关键问题之一在于阈值参数的选取,然而在以往文章中,无论是采用傅里叶变换还是曲波变换作为稀疏基,都没有详细的研究阈值参数对重建结果的影响,尽管在这些文章中都保证了在每次迭代过程中阈值不断减小,然而不同的下降阈值公式其收敛速度不一样。为此,本文在前人研究的基础上对不同的阈值参数公式进行研究,采用曲波变换作为稀疏表示基,提出了新的阈值参数公式,取得了满意的重建效果。
1 问题陈述
地震数据重建主要通过采样矩阵得到某未知信号在该矩阵下的线性测量值。为此,假设如下线性正演模型
yobs=Mf
(1)
其中yobs∈Rn表示不完整的地震数据;f∈RN,且N≥n,表示需要重建的完整地震数据;M∈Rn×N为采样矩阵,希望能由不完整的测量数据yobs恢复出完整的地震数据f。为此,采用多尺度多方向曲波变换对地震数据进行稀疏,假设曲波变换用C表示,则地震数据f在曲波域C中的稀疏表示是系数x,方程(1)可以写成
yobs=MCHx
(2)
其中H表示共轭转置矩阵,因此,需要采用一定的算法从随机缺失地震数据的稀疏系数x中重建出无假频的数据f,并且保证重建精度满足后续处理的要求。
2 阈值迭代算法
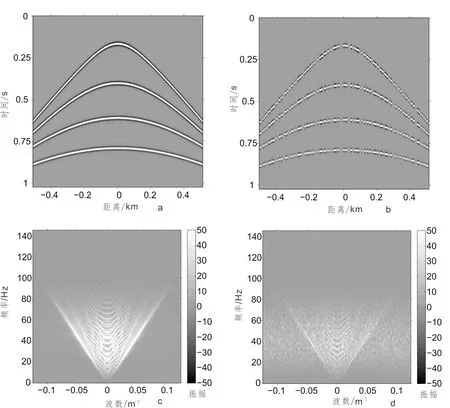
图1 原始模型采样及f-k频谱Fig.1 Original model and the frequency spectruma.理论模型;b.50%随机欠采样;c.理论数据f-k频谱;d.随机采样数据f-k频谱
要从测量信号yobs中恢复出原始信号的全部信息,直接的办法就是通过不断优化进行求解l0范数,而由于上式的求解是一个欠定的病态问题,不容易得到精确解。但在一定条件下,l1最小范数和l0最小范数可以得到同样的近似解。那么方程(2)就可以变为l1最小范数模型,即:

(3)
实际上,地震数据重建的关键技术之一,就是通过最小化策略求解上述欠定问题。为表述和求解方便,可将其写为以下形式

(4)
对于方程(4)的解,阈值因子λ的选用特别关键,因为它的作用直接影响到该方程中l1范数和l2范数两项之间的权重。因此,在数据重建过程中,阈值参数λ需要不断地促进变化,直到最终解满足一定的精度要求。为此,可以采用阈值迭代法进行求解(Candes et al., 2005),其迭代式如下:
xn=Sλ(xn-1+AT(y-Axn-1))
(5)
这里Sλ取软阈值函数,x初始值可以设置为零。该式在每次迭代过程中都会更新阈值,最小化(4)式中的二次方项,继而可通过阈值法投影到l1球上,不断收敛到方程(4)的解,直到满足精度要求,再对N次迭代后的系数xn做曲波反变换就可以恢复缺失道信息。

图2 线性和指数阈值重建结果及f-k频谱 Fig.2 Reuslts of different threshold parameter and frequency spectruma.线性阈值参数;b.指数阈值参数;c.线性阈值重建后的频谱d.指数阈值重建后的频谱
在解上述非线性问题过程中,首先需要保证阈值较大以强调稀疏促进的l1项,随着迭代次数增加,需要使l2项在求解过程中的占较大影响,为此,使阈值因子λ慢慢递减,通过不断的迭代过程,逐渐逼近真实解。因此,阈值参数的选取工作尤为重要。一般来讲,在阈值迭代过程中,阈值参数λ1满足,‖Cy‖∞=λ1>λ2>…>ε,式中ε为接近0的小值。常用的线性阈值参数λi可由下式确定:
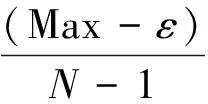
(6)
式中Max为|Cy|的最大值,即稀疏变换系数绝对值的最大值。
采用方程(6)所述的线性阈值公式最终可以重建出缺失道,然而在求解过程中,收敛速度较慢,从而导致该方法不能大规模工业生产应用。为此,本文提出按指数λ1规律衰减的阈值参数,使得阈值参数逐渐下降的幅度更大,保证了求解的精度,并且收敛速度更快,节省计算工作量,该阈值参数公式为:
3 理论模型
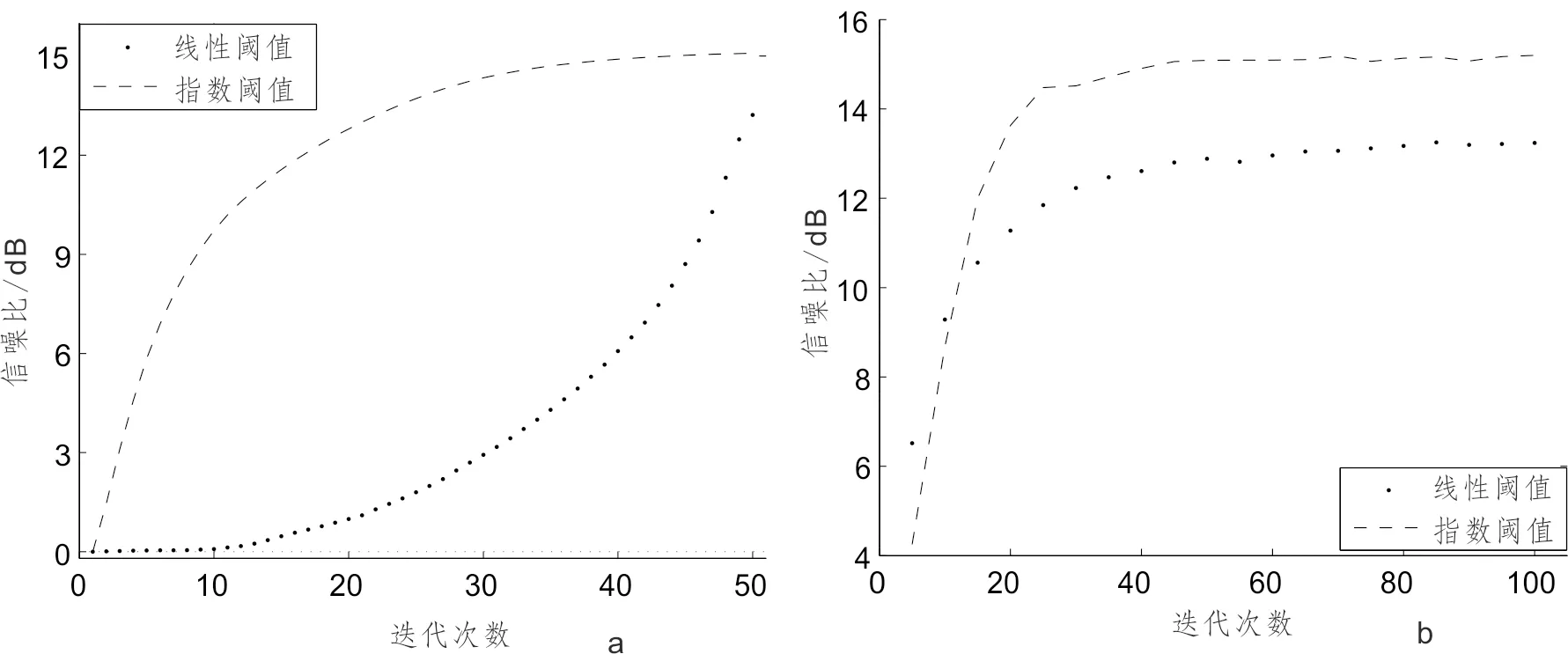
图3 迭代次数与信噪比关系曲线图Fig.3 The graph of SNR and iteration number after reconstructiona.迭代次数固定,每次迭代与信噪比图;b.最大迭代次数不同时,迭代次数与信噪比图
为了分析采用曲波变换后的指数阈值迭代法重建效果,定义信噪比公式SNR=20log10‖x0‖2/‖x-x0‖2,其中x0表示完整数据模型,x表示恢复结果,该值越高,表明重建精度越高。图1a为256道合成地震记录,该记录总共有4层地震反射波,每一层反射波能量有所差异,采样间隔为1 ms,道距为4 m,每道1 024个采样点,然后对其进行随机欠采样以模拟野外数据缺失过程。图1b为对模型数据进行50%随机欠采样后的缺失道地震数据剖面图,图1c为原始理论数据的f-k频谱,图1d为欠采样后的f-k频谱,从中可以看出随机欠采样会产生不相干的随机噪声,从而影响到了有效波的振幅能量,必须对其进行叠前重建,恢复缺失地震道能量,提高地震剖面的信噪比,满足后续处理的要求。为此,采用曲波变换作为地震信号的稀疏基,引入阈值迭代算法进行求解计算,分别采用上述线性阈值和指数阈值进行重建。图2a为采用线性阈值参数的重建结果,图2b为指数阈值参数重建的结果,重建后的信噪比分别为13.22 dB和15.08 dB,其中迭代次数都为50次,曲波变换的尺度数为5,方向值为16,图2c和图2d分别为其f-k频谱。从以上结果可以看出,线性和指数阈值参数都可以将缺失道信息有效地恢复出来,并且频谱能量与原始数据非常接近,能量损失较少。但是从计算时间和重建的精度来看,本文所提出的指数阈值参数计算效率快,并且重建后的精度高于线性阈值近2 dB。尽管如此,由于随机欠采样没有约束,采样点完全随机,造成局部连续缺失道较多,使得在地震同相轴弯曲较大的区域则重建精度不高,如图2b中的第一条反射波同相轴近道部分能量没有得到有效地收敛,局部误差较大,这种情况下需要利用其它空间方向的信息进行重建,以弥补单一方向的不足。
为了进一步比较线性阈值参数和指数阈值参数重建后精度以及它们的计算效率,再对图1b进行重建处理。图3a表示采用50次迭代时信噪比与迭代次数关系曲线图,它表示了每次迭代后两种阈值参数重建结果的信噪比,从图中可知指数阈值参数在每次迭代过程中重建后的信噪比都高,而线性阈值参数则信噪比相对较低。然后采用最大迭代次数5~100次进行分别重建,并且每次迭代次数都为5的倍数进行增加,从而计算这两种阈值参数分别重建后的信噪比,图3b为两种阈值参数每次最大迭代次数与信噪比关系曲线图,如果想要得到重建后信噪比为13 dB的计算结果,线性阈值参数需要经过至少迭代50次,从而使得计算速度慢,不能处理海量的地震数据。而本文提出的阈值参数只需迭代18次左右,节省一大半计算时间,对于处理海量的地震数据具有明显的优势。整体上来讲,随迭代次数的增大,这两种阈值参数重建后的信噪比都会增加,但重建后在相同的信噪比基础上,迭代次数太多显然浪费计算时间,所以,不论从计算时间还是从重建后的信噪比来讲,本文所提出的指数阈值参数公式具有较大优势。当迭代次数超过一定值时,信噪比的增量变化不大,因此为了提高计算效率,本文指数阈值参数在随后的重建处理中采用50次迭代。

图4 含噪地震数据及其重建结果(50%地震道缺失)Fig.4 Noisy seismic data and reconstruction result (50% missing)a.含噪理论模型;b.50%随机欠采样;c.由图4b重建结果;d.图4c与原始含噪模型误差
由于野外地震数据噪声一般比较发育,需要检验本文方法在噪声较为发育下的重建效果。为此,在原始数据中加入一定比例的高斯随机噪声以模拟野外含噪地震记录,其加噪结果如图4a所示。然后对其进行50%一维随机欠采样,从而生产了大量的含噪缺失道,如图4b所示,然后采用本文高精度指数阈值迭代法的对该含噪缺失道数据进行重建,检验在噪声较为发育情况下本文方法的重建效果。图4c为采用本文指数阈值参数迭代法的重建结果,重建后信噪比6.23 dB,含噪缺失地震道的全部信息都得到了较好的恢复,重建后的地震波同相轴非常连续,信噪比显著提高。图4d为重建后的地震剖面与原始加噪理论地震剖面的误差剖面图,从误差剖面图可以看出该剖面主要为噪声能量,表明重建前后的有效信息能量损失较小,有效波信号恢复效果较好,说明基于本文所提出的高精度指数阈值迭代法在含噪地震数据重建中具有较强的抗噪能力,满足处理实际资料的需要。
4 实际应用
为了检验本文方法的应用效果,特意对某区野外实际资料进行处理,图5a为实际地震单炮记录图,该地震数据道距25 m,采样率4 ms,180道接收。首先对原始单炮记录进行50%随机欠采样,欠采样结果如图5b所示,然后采用本文方法对野外缺失道地震数据进行高精度重建,其中迭代次数为50次,曲波变换的尺度数为5,方向值为16。图5c为本文方法重建后的结果,其信噪比为9.89 dB。在欠采样50%的情况下,本文方法重建效果较好,缺失道信息得到了有效的恢复,并且弱能量有效波也得到了较好的保护。图5d为重建后地震记录与原始单炮记录的误差剖面图,可以看出,除了在近道处误差相对较大外,其他区域有效波能量损失较少。为了进一步从频率域分析重建前后的能量损失情况,特意将其f-k频谱图进行显示(图6)。从图6中也可以看出,本文方法重建后f-k谱有效波能量损伤最小,效果显著。整体上来看,本文方法重建后地震波同相轴非常接近于原始实际地震记录,提高了地震记录的信噪比,完全可以满足高分辨率地震勘探的要求。

图5 野外数据重建过程(50%地震道缺失)Fig.5 Reconstruction result of the field data(50% missing) a.实际单炮记录图;b.随机欠采样记录图;c.本文方法重建结果;d.重建误差剖面
5 结论
本文采用曲波变换作为稀疏表示基,引入阈值迭代算法进行重建,取得了较好的重建效果。通过研究可知,在得到同样的重建精度时,传统线性阈值迭代的重建方法效果有限,所需计算时间较多。而本文采用指数阈值迭代的进行数据重建,则可以得到了高精度的重建效果。通过理论对比分析表明本文方法在相同迭代次数下能够得到更高的信噪比。而重建后达到相同的信噪比时,则所需要的迭代次数较少,节约了计算时间,从而使得本文方法具有参数设置简单、用时少、精度高等特点,并且在实际资料的应用中也得到了较好的重建效果。
从本文的重建结果可以看出,由于曲波变换能够反映地震信号的局部特征,更加稀疏的表示地震信号的波前特征,可以得到更好精度的重建结果,但是曲波变换冗余度高,与傅立叶变换相比,运算速度较慢,尽管本文提出了指数阈值参数公式,但在处理大量地震数据时还是会受到速度限制,因此也需要进一步优化算法,以达到工业化生产的需要。

图6 重建过程中的地震数据f-k频谱图Fig.6 The f-k spectrum of reconstruction processesa~c分别为图5a~5c的f-k频谱图
陈晓, 周磊, 于鹏, 等. 2016. 基于模拟退火算法的大地电磁和地震数据贝叶斯联合反演[J].东华理工大学学报:自然科学版,39(1):59-66.
高建军, 陈小宏, 李景叶. 2011. 三维不规则地震数据重建方法[J]. 石油地球物理勘探,46(1):40-46.
黄光南,邓居智,李红星, 等. 2016. 三维VSP地震初至波走时层析成像研究[J]. 东华理工大学学报:自然科学版,39(3):266-272.
徐卫, 张华, 张落毅. 2016. 基于复值曲波变换的地震数据重建方法[J]. 物探与化探,40(4):750-755.
张华, 陈小宏. 2013. 基于jitter采样和曲波变换的三维地震数据重建[J].地球物理学报,56(5):1637-1649.
Berg E D,Friedlander M P.2008. Probing the Pareto frontier for basis pursuit solutions[J]. SIAM J.on Scientific Computing,31(2):890-912.
Candes E J, Romberg J. 2005. Practical Signal Recovery from Random projections[J]. Proceedings of SPIE Computational Imaging III, 23(2):76-86.
Herrmann F J, Hennenfent G. 2008. 1Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 73(1):233-248.
Zhang H, Chen X H, Li H X. 2015. 3D seismic data reconstruction based on complex-valued curvelet transform in frequency domain[J]. Journal of Applied Geophysics, 113(6):64-73.
Zhang H, Chen X H, Wu X M. 2013. Seismic data reconstruction based on CS and Fourier theory[J]. Applied Geophysics, 10(3):170-180.
HighPrecisionReconstructionofSeismicDataBasedonExponentialThresholdIterationMethod
ZHANG Hua, YANG Hui, DIAO Su, LIU Jun
(State Key Laboratory Breeding Base of Nuclear Resources and Environment,East China University of Technology,Nanchang,JX 330013, China)
During the data acquisition of seismic exploration, the phenomenon of missing traces are unavoidable. In order to meet the requirements for subsequent processing and interpretation, missing data reconstruction is essential preprocessing steps in any seismic data processing chain. The data reconstruction method based on the exponential threshold iterative method has been introduced in the paper. Firstly, multi-scale and multi-directional curvelet transform to characterize the local features of seismic data has been introduced and the threshold iterative method is adopted. Meanwhile, a soft thresholding is introduced to remove the random noise arisen by the undersampling. Aiming at the disadvantage of slow convergence in traditional threshold parameter during the reconstruction process, an new exponential decreased threshold is also proposed and it can reduce iterations and improve reconstruction efficiency. The simulation results on synthetic seismic data showed that this method has a better effect and faster computation. At last, we apply this technology into real seismic data and obtain a good result.
curvelet transform; soft Threshold; data reconstruction; threshold iterative method
P631
A
1674-3504(2017)03-0253-08
2016-12-07
国家自然科学基金(41304097,41664006);江西省自然科学基金(20151BAB203044, 20171BAB203031, 20171BAB202028);江西省杰出青年人才资助计划(20171BCB23068)
张 华( 1979—),男,博士,副教授,研究方向为数据重建及规则化反演。E-mail: zhhua1979@163.com
10.3969/j.issn.1674-3504.2017.03.006
