海洋可控源电磁法2.5维有限元正演模拟研究

韦艳刚， 郭荣文， 刘 颖， 柳建新

(1.中南大学 地球科学与信息物理学院，长沙 410083;2.中国海洋大学 海洋地球科学学院，青岛 266003)

海洋可控源电磁法2.5维有限元正演模拟研究

韦艳刚1， 郭荣文1， 刘 颖2， 柳建新1

(1.中南大学 地球科学与信息物理学院，长沙 410083;2.中国海洋大学 海洋地球科学学院，青岛 266003)

为了消除源点的奇异性问题，在源点利用delta函数离散。设计一维的层状模型，验证海洋可控源 2.5D 有限元数值模拟算法的正确性和精度；考虑到在海中洋流、海底地形起伏变化大以及海底介质电性结构复的影响，海洋可控源电磁的发射源会发生倾斜、旋转、位置偏离测线，因此定义了任意取向的发射源。实际应用证明，发射源姿态变化以及不同发射频率和油气层参数,对海洋可控源电磁场响应都有很大地影响。

海洋可控源电磁法; 2.5维; 有限元; 发射源

0 引言

海洋可控源电磁法(controlled-source electromagnetic methods,CSEM)，是勘探海底油气资源和地质构造研究的一种海洋地球物理方法。在上个世纪80-90年代，海洋可控源电磁法在海洋地壳和上地幔等领域中得到广泛地应用[1-2]。在近十多年里，由于海洋可控源电磁法对高电阻率储层具有很强的探测能力，其在海洋油气资源和海底天然气探测中也发挥着重要的作用[3-4]。目前已有不少关于海洋可控源电磁法的文章被发表，在海洋可控源电磁法正演模拟方法研究的初期，主要以一维模型正演为主，但是1D正演方法不适合探测海底较为复杂的结构。对于三维模型,虽然Newman等[5]、Weiss等[6]使用交错网格有限差分法可以模拟三维不均匀结构模型，但是这种方法采用结构化网格，计算的精度和速度并不能满足当代的工作需求。

实际情况下，将三维问题转化为二维问题，大大减少计算机内存，提高计算速度，并且Ali Moradi Tenhrani等[5]分析了不同海底储层大小、不同埋藏深度和不同发射频率对2.5D和3D海洋电磁场的影响。结果分析表明，2.5D海洋可控源电磁响应与3D电磁响应的相对误差非常小，应用2.5D海洋可控源电磁法代替3D是具有合理性的，推动了2.5D海洋可控源电磁法的快速发展。

通过有限元法离散得到一个大型、稀疏、复系数对称线性方程组，求解大型稀疏线性方程组的方法有很多种，而很多学者经过广泛深入地研究[6-12]，Krylov子空间方法是最受欢迎的方法。Roland W.Freund等[13]提出了Quasi-Minnimal Residual(QMR)方法。这种方法基于Lanczos双共轭过程，核心思想是极小化处在Krylov子空间的解的残量范数的短递归方法。Weiss[14]首次将QMR法运用到3D电磁感应线性方程组求解,QMR法在迭代求解中数值能够平滑稳定收敛并且逼近解的准确残量范数，不需要显示系数矩阵的存储，因此减小了内存空间，大大提高线性方程组的求解速度。

在海洋可控源电磁法探测过程中，由于海底水流动性和仪器本身等问题，发射源容易发生旋转和倾斜，场源形态的变化均会对海洋CSEM数据产生影响。Streich等[15]认为发射源方位和位置偏差等对电磁场响应产生影响，因此我们引入了水平旋转角θ和倾角Φ来定义任意取向的发射源，分别讨论发射源发生旋转以及倾斜与无旋转倾斜时对探测油气层的影响。

笔者基于麦克斯韦方程组出发，推导出2.5D海洋可控源电磁法波数域电磁场的耦合微分方程；通过有限元法进行数值离散得到一个大型线性方程组，使用QMR法迭代求解。先设计一维的层状模型，验证海洋可控源 2.5D 有限元数值模拟算法的正确性和精度，并考虑电偶极子发生偏差与无偏差时误差。最后采用最优观测方式探索不同海底储层大小、不同埋藏深度和不同发射频率，对海底探测油气层的影响。

1 方法理论

1.1 异常场方程

为了消除源点的奇异性问题，在有限元中应用叠加原理，将电磁场分解由电偶源在一维水平层状(电导率σp)中产生的一次场(EP和HP)和由二维异常体(电导率为σs=σ-σp)产生的二次场(ES和HS)：

E=EP+ES,H=HP+HS

(1)

设计一个二维海洋地电模型，其走向方向假定为沿x轴,垂直向下的方向为z轴,与x轴相垂直的是y轴，水平电偶源位于海底上方海水中。假定时间因子为 e-iωt,似稳态情形下，二次场满足偏微分方程：

▽×ES=iωμ0HS

▽×HS-σES=σSEP

(2)

式中：E为电场强度(V/m);H为磁场强度(A/m);μ0=4π×10-7(H/m)为介质磁导率；ω为角频率；σ为介质电导率张量(S/m)

通过傅立叶变换，场可以转换为：

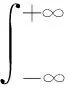
(3)

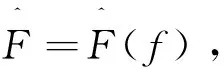
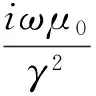
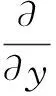
(4)

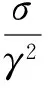
(5)

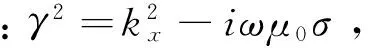
1.2 有限元方程

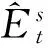
(6)

(7)

式中:n表示边界上的外法线单位向量；ny和nz分别表示沿着y轴和z轴的单位向量。

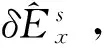
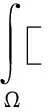
(8)

利用矢量公式

a▽·b=▽·(ab)-▽a·b

(9)

和散度公式

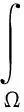
(10)

以及格林公式

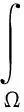
(11)

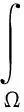
(12)

方程(8)则变成为

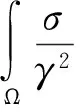
(13)

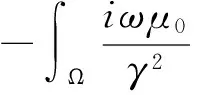
(14)

将求解区域分解成ne个三角单元，单元编号记为e=1、2、…、ne。方程(13)和方程(14)的积分则分解为各个单元积分之和：

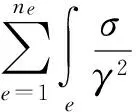
(15)

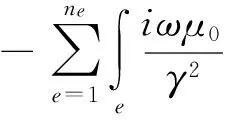
(16)

采用规则的矩形单元对模拟区域进行有限元离散，在单元积分内采用双线性插值,得到一个大型、稀疏、复系数对称线性方程组Ku=p，对其优化处理后采用QMR(Quasi-Residual-Method，拟最小残差法)迭代求解,分别得到总场和二次场各个分量。

2 源点奇异性处理

海洋可控源电磁法与大地电磁法最大的区别，在于引入人工源，源的处理一直是一个难点。在不需要源点附近增加网格数量的前提下，避免源点在远处产生奇异性，而获得高精度的有限元解，需要采用 HERRMANN[16-17]提出的伪δ函数来等效场源的作用，其中伪δ的函数表达式为式(17)。

(17)

其中:x为离散点坐标；x0为中心点坐标；参数τ是控制源分布宽度和幅值的参数。显然，使用伪δ函数描述源项，可使总体方程右端项不为“0”的节点增多，改善了总体方程组的不稳定性，可以精准地模拟场源的分布，提高计算精度。

3 任意取向发射源的定义

海洋可控源电磁法采用船载可移动水平电偶极子源在海水上方一定高度上匀速前进，由于海底洋流和电缆本身重量等问题,不可能达到精确的水平沿测线方向,会存在一定的偏差,因此发射源取向往往是任意的。

如图1所示,假设定义发射源水平旋转角θ为电偶极子源沿顺时针方向朝y轴旋转的角度,发射源倾角Φ为电偶极子源朝z轴正向偏离xoy面的角度。发射源沿x方向布置时(HED-x),此时为赤道装置(broadside 观测),激发的电场主要为x分量，y分量和z分量十分微弱，当发射源沿y方向布置时(HED-y),此时为轴向装置(inline 观测),激发的电场主要为y分量，x分量和z分量极微弱，发射源沿z方向布置时,倾角φ=90°,为垂直偶极源(VED)。

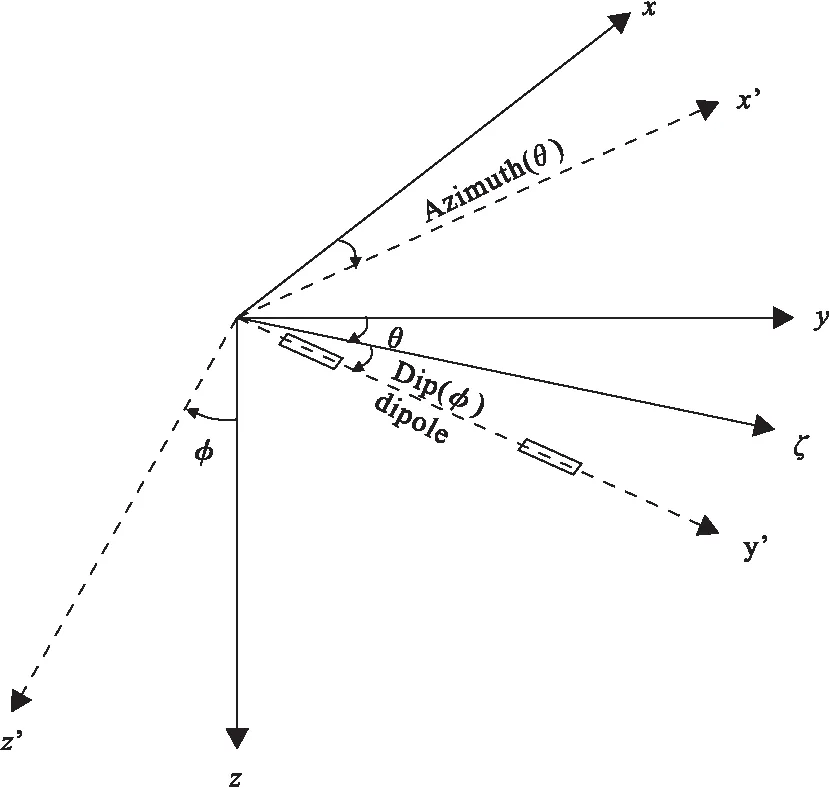
图1 电偶极子方位示意图Fig.1 The orientation of an electric dipole

4 数值计算

4.1 算法正确性检验—一维层状模型的计算

为了验证算法和程序的正确性，计算一个高阻储层的一维经典模型(Constable[21]),如图2所示,海水电阻率为0.3 Ω·m,海底深度为 1 000 m ;海底下方为 1 000 m 有一个厚度100 m电阻率为100 Ω·m的高阻油气薄层；油气层上方与下方均为岩层，其电阻率为1 Ω·m;电偶源布置于海底上方50 m处,长度为1 m,发射电流为1 A ,频率为0.25 Hz ;测线沿着y方向布置，测线长度为12 km，共有121个接收点,间隔为100 m均匀布置于海底。

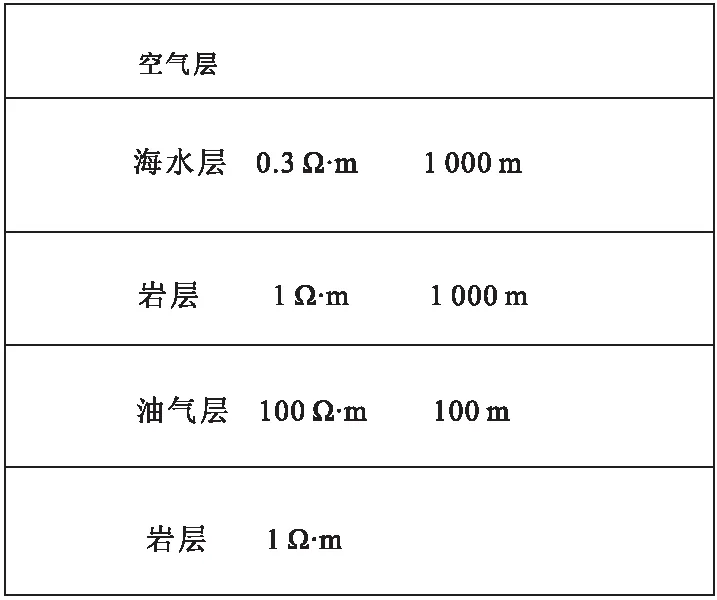
图2 1D层状模型Fig.2 1D layered model

计算结果如图3所示，将本文计算的电磁场分量的振幅、相位与水平层状模型的一次场解析解做对比，其中图3(a)、图3(b)、图3(e)、图3(f)分别为轴向装置(发射源沿y方向布置)所对应的Hx、Ey、Ez分量振幅相位及其误差，图3(c)、图3(d)、图3(g)、图3(h)分别为赤道装置(发射源沿x方向布置)所对应的Ex、Hy、Hz分量振幅相位及其误差。由于在海洋CSEM勘探中,发射天线通常由较长的导线构成，此时若仍将发射源看作电偶极子源，将导致在源点附近的电磁场计算结果存在明显误差。从图3(a)～图3(h)可以发现，与1D解析解算法相比，在收发距较小的情况下，电磁场分量的振幅及相位误差都比较大，但除在小收发距处外，各个分量振幅的相对误差都小于4%，相位绝对误差都小于5°，有限元解与解析解吻合得比较好，说明本文的算法和程序是正确的和有效的。通过计算和对比inline 观测与broadside 观测的电磁场响应，我们得到一个结论，inline 观测得到振幅相对误差和相位绝对误差比broadside 观测小，并且在偏移距较远时，都趋向于0，inline 观测为电磁场响应较优的观测方式。

4.2 发射源位置偏离对海洋CSEM响应的影响

由于发射源方向的任意性，为了研究发射源位置偏离对海洋CSEM响应的影响，采用图2 的一维层状模型进行模拟，分析不同水平旋转角和倾角海洋CSEM响应的影响。图4左边为倾角φ=0°，水平旋转角θ=90°、87°、85°、83°、81°得到的电磁场振幅值，右边以θ=90°，φ=0°为基准，水平旋转角偏差为3°、5°、7°、9°与水平旋转角无偏差的误差图。当发射源由y轴逐渐向x轴旋转时，点偶极矩在y轴上的投影越来越小，使得y方向上的电场分量越来越小。从图4右边发现，随着偏移距的增大，振幅的相对误差越来越小，但是水平旋转角偏离的角度越大，振幅的相对误差就越大，当水平旋转角偏离9°时，在收发距小于2 500 m时，y方向的电场和z方向的磁场的振幅相对误差都接近于10%，相比较而言，水平方向的磁场受角度的影响较小，因此在实际海洋CSEM勘探中，在小偏移距下水平旋转角偏离测线大于9°时，有必要将发射源进行调整或者计算时考虑误差的存在。

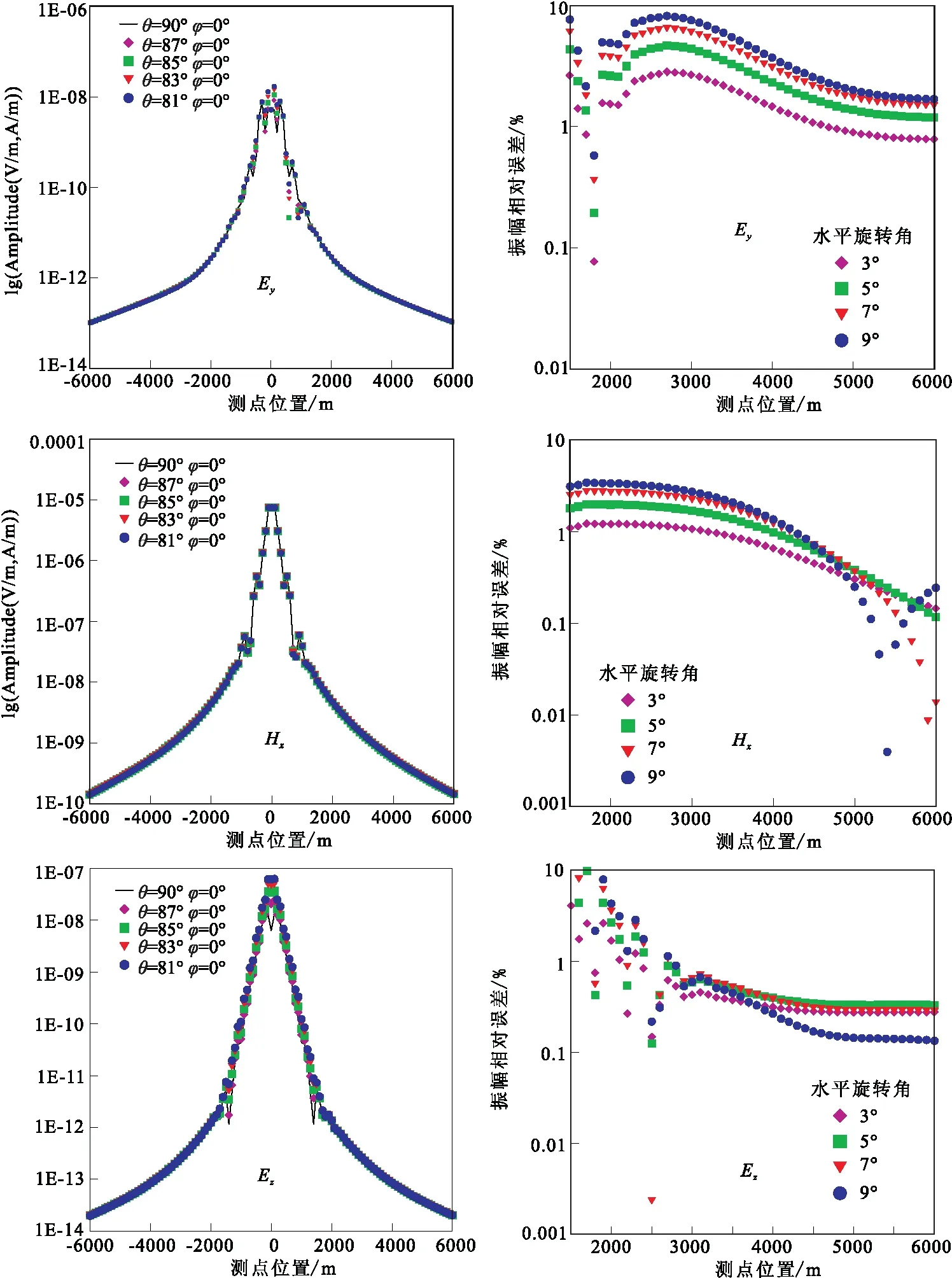
图4 1D模型不同水平旋转角振幅及振幅相对误差Fig.4 Different horizontal rotation angle amplitude and it’s relative errof of 1D model

4.3频率及油气层模型参数对2.5DMCSEM电磁响应的影响

模拟一个二维海洋地电模型。如图5所示，空气电阻率设为1012Ω·m，空气层下方有厚度为1 000 m的海水层，电阻率为0.3 Ω·m，海底埋深1 000 m处有一个电阻率为100 Ω·m的油气层，其长为4 000 m,高为100 m,在y轴上范围从-2 000 m到2 000 m,在z轴上的范围从1 000 m到1 100 m，围岩电阻率为1 Ω·m，发射源位置为海底上方50 m，y= 0 m处,在海底共有 121个接收站，分布范围在y轴上从-6 000 m到6 000 m,间隔为100 m。

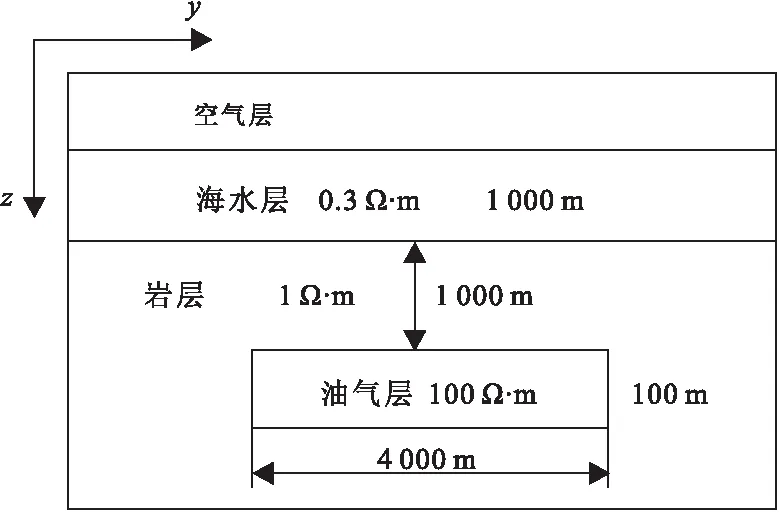
图5 2D油气模型Fig.5 The 2D reservoir model

在图5二维油气模型基础上，图6为inline 观测下y方向的电场在不同发射源频率,不同油气层的厚度,不同油气层的埋藏深度,不同油气层的水平长度振幅的相对误差，设计0.25 Hz、0.1 Hz、1 Hz三个发射频率，在图6(a)中发现，不同的发射频率电场振幅的相对误差不同，随着发射频率的增大，Ey振幅的相对误差也增大，在偏移距较小尤其明显，f=0.25 Hz所得到振幅的相对误差比较小，因此选择适当的频率对海洋可控源电磁法的观测有着重要的意义。在图6(b)～图6(d)中，在发射频率为0.25 Hz下，不同油气层的厚度，不同水平长度以及不同油气层埋藏深度的得到的y方向的电场的振幅相对误差接近吻合，因此，不同油气层的厚度，不同水平长度以及不同油气层埋藏深度，对2.5DMCSEM响应的影响不大。

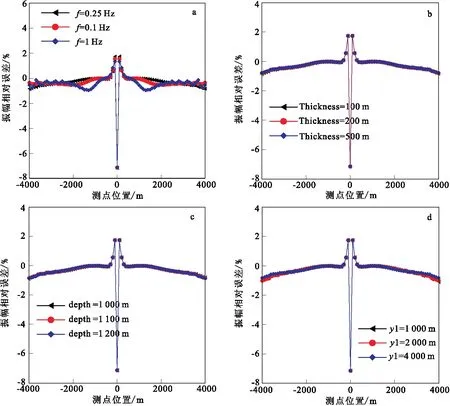
图6 在不同发射频率、不同埋藏深度和不同海底储层大小下Ey振幅相对误差Fig.6 Eymplitude relative error for different frequencies of the emitted field. different depths of the reservoir and different size of the reservoir(a)不同发射源频率；(b)不同油气层的厚度；(c)不同油气层的埋藏深度;(d)不同油气层的水平长度

5 结论与讨论

笔者详细推导了有限元2.5D海洋CSEM电磁场响应，采用叠加原理，并验证算法的正确性和有效性。在一维层状模型探测中，inline 观测较broadside 观测反应灵敏。

发射源位置的偏离对海洋可控源电磁响应影响较大，尤其是在收发距较小的情况，水平方向的电场振幅随着偏离角度的增大而增大，当偏离角度达到9° 时，振幅相对误差接近10%，在实际海洋CSEM勘探中，偏离角度较大时有必要考虑对海洋可控源电磁响应影响。

发射频率对海洋可控源电磁响应影响较大，针对海洋可控源电磁法的工作频率范围0.001 Hz ～10 Hz，设计0.25 Hz、0.1 Hz、1 Hz三个发射频率，在上述模型中，f=0.25 Hz是比较适当的发射频率，在海洋可控源电磁响应中选择适当的频率很重要。

[1] YOUNG P D,COX C S.Electromagnetic active source sounding near the East Pacific Rise[J].Geophysical Research Letters,1981(8):1043-1046.

[2] MACGREGOR L M, CONSTABLE S, SINHA M C. The RAMESSES experiment III: Controlled-source electromagnetic sounding of the Reykjanes Ridge at 57°45’57N [J]. Geophysical Journal International, 1998,135:773-789.

[3] EIDESMO,T.S.ELLINGSRUD,L.MACGREGOR,et al. Sea bed logging(SBL), a new method for remote and direct identification of hydrocarbon filled layers in deep water areas[J]. First Break,2002(20):144-152.

[4] CONSTABLE S, WEISS C J. Mapping thin resistors and hydrocarbons with marine em methods: Insights from 1D modeling[J]. Geophysical, 2006,(71): G43- G51.

[5] ALI MORADI TENHRANI, EVERT SLOD. Applicability of 1D and 2.5D marine controlled source electromagnetic modelling[J]. Geophysical Prospecting, 2013(61):602-613.

[6] LI Y, DAI S. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures[J]. Geophysical Journal International, 2011,185:622-636.

[7] SAAD Y,SCHULTZ MH.GMRES:A generalized minimal residual algorithm for solving nonsymmetric linear systems[J].SIAMJ. Sci.Stat.Comput,1986(7):856-869.

[8] ROL,W.FREUND,NOEL M.NACHTIGAL,QMR: a quasiminimal residual method for non-Hermitian linear systems[J].Numer,Math,1991,60:315-339.

[9] FREUND R W,HOCHBRUCK M.On the use of two QMR algorithms for solving singular systems and applications in Markov chain modeling[J].Numerical Linear Algebra with Applications,2010,1(4):403-420.

[10] A.ESSAI,WEIGHTED FOM.Gmres for solving nonsymmetric linear systems[J].Numer, Algorithms,1998(18):277-292.

[11] Z.H.CAO, X.Y.YU. A note on weighted FOM and GMRES for solving nonsymmetric linear systems[J]. Appl.Math.Comput,2004,151:719-727.

[12] SAAD Y. Iterative Methods for Sparse Linear Systems[M]. second edition, SIAM, Philadelphia,2003.

[13] FREUND R W. Nachtigal N M. QMR: a quasi-minimal residual method for non-Hermitian linear systems[J]. Numerische Mathematik, 1991, 60(1):315-339.

[14] WEISS C J. A Matrix: free Approach to Solving the Fully 3D Electromagnetic Induction Problem[J]. Seg Technical Program Expanded Abstracts, 2001, 20(1):1451.

[15] STREICH R,MICHAEL B.Electromagnetic fileds generted by finite-length wire sources:comparison with ponit dipole solutions[J].Geophysical Prospecting,2001,59(2):361-374.

[16] HERRMANN R B. SH-wave generation by dislocation source-A numerical study[J]. Bulletin of the Seismological Society of America,1979, 69(1):1-15.

[17] 张继锋,汤井田,喻言,等.基于二次插值的线源可控源有限元数值模拟[J].吉林大学学报,2009,39(5):929-935.

ZHANG J F, TANG J T, YU Y, et al. Finite element numerical simulation of controlled-source based on the quadratic interpolation line source[J].Jilin university journals,2009,39(5):929-935.(In Chinese)

2.5Dfiniteelementmodelingofmarinecontrolled-sourceelectromagneticfields

WEI Yangang1, GUO Rongwen1, LIU Ying2, LIU Jianxin1

(1.Central South University, School of Geosciences and Info-Physics，Changsha 410083，China;2.Ocean University of China, College of Marinca Geosciences, Qingdao 266003，China)

To eliminate singularity of source point, the delta function is used in discrete source point. We have designed a one-dimensional layered model to test the correctness and accuracy of marine controlled source's 2.5 D ( finite element method) algorithm. In the midst of the ocean currents, considering the influence of ocean current, fluctuation of seabed topography and electrical structure of seabed, the emission source of marine controlled electromagnetism will incline, rotate and deviate from the line. Therefore, we define the emission source with arbitrary orientation. The practical application shows that the variation of emission source attitude and the different emission frequency and reservoir parameters have great influence on the electromagnetic response of marine controlled source.

marine controlled-source electromagnetic method; 2.5 D; finite element; emission source

P 631.2

A

10.3969/j.issn.1001-1749.2017.05.01

2016-10-18 改回日期： 2016-11-07

国家自然科学基金(4167407965,4167408070)

韦艳刚(1991-)，女，硕士，主要从事海洋可控源电磁法研究，E-mail：1312877493@qq.com。

郭荣文(1980-)，男，副教授，主要从事电磁法勘探研究，E-mail：573377360@qq.com。

1001-1749(2017)05-0579-08