波流耦合下保守污染物迁移扩散的模拟研究

王平，邹文峰

（1.国家海洋环境监测中心，辽宁大连116024；2.大连中交理工交通技术研究院有限公司，辽宁大连116023）

波流耦合下保守污染物迁移扩散的模拟研究

王平1，邹文峰2

（1.国家海洋环境监测中心，辽宁大连116024；2.大连中交理工交通技术研究院有限公司，辽宁大连116023）

基于三维潮流和谱波浪模型，以及输移扩散模型和拉格朗日粒子追踪模型，构建了波流耦合下保守污染物的迁移扩散模型。模型基于非结构化网格，对近岸复杂岸线有很好的拟合，可用于大范围波流耦合计算。运用所建的耦合模型研究了旅顺港内外的潮流变化、波生流场、保守污染物输移、粒子运动、以及新水道对湾内污染物迁移的影响，模拟的潮流场与实测数据吻合较好。结果表明：潮流会在湾内近湾口处形成一逆时针涡，波浪对湾内影响较小，但波生流会改变湾口流场分布；在湾内处于涡中的水体潮流自净能力较强，而湾中及湾底则较弱，SE向波浪会降低湾内水体的自净能力；新潮流通道的开挖，会显著改善水体的自净能力，尤其对湾底浅水区域作用明显。

波流耦合；波生流；污染物迁移；Lagrange；数值模拟

在近岸海域，随着水深变浅，潮动力逐渐减弱，波浪的作用逐渐增强。波浪在近岸破碎引起的波生流成为近岸水动力环境的主要影响因素之一，对近岸海域污染物的迁移和扩散有很大的影响，建立波流联合作用下的近岸污染物迁移扩散研究模型已尤为必要。

近岸波流耦合计算，可以分成波浪和潮流单独计算以及两者影响参数相互传递两个过程。针对流对波浪的影响，Wei（2005）、张洪生（2007）和郑金海等（2008）分别利用含流缓坡方程和波能守恒方程模拟了流场作用下的波浪传播变化；而波浪对流的影响，研究均基于辐射应力理论进行，如Sun等（2009）和Tang等（2008）在矩形网格下实现了近岸波生流的模拟；Wu（1985）和唐军等（2010）在三角型网格下建立了波生流模型，波浪模型是基于椭圆形缓坡方程，其空间步长受制于波长的限制。

目前对实际海域的污染物迁移扩散的研究，大都只考虑潮流的影响，如王昆等（2010）对辽东湾海域中水体污染物的数值计算，王平等（2013）也单独考虑过潮流对大连湾保守污染物输运的作用，Shen（2007）和Doos等（2007）对不同海域的水体水龄以及示踪物输移时间的研究，上述研究对不同海湾中污染物迁移和水质变化有很好的模拟结果，但均未考虑波浪的影响。Tang（2008）等建立了近岸波生流模型并研究了污染物在波生流场中的运动规律，但未对实际海域进行研究；Sun等（2005）研究了渤海沿岸局部区域波生流场中的污染物输移规律，但未考虑耦合潮流的影响，且只是针对波生流下污染物输移方向的单一研究。

基于上述考虑，耦合三维潮流和谱波浪模型，同时结合拉格朗日粒子追踪法和输移扩散模型，建立了近岸波流耦合作用下保守污染物迁移扩散的数值研究模型。其中波浪模型基于波作用谱守恒方程，在空间上离散不受波长限制；耦合模型基于非结构化网格离散，对近岸复杂岸线能很好的拟合。利用该模型研究了波流耦合下旅顺港湾内外的潮流形态、波生流场、Lagrange粒子运动、保守污染物迁移规律以及新水道对湾内水体潮流自净能力的改变。

1 数值模式

1.1 近岸波浪模型

波浪计算控制方程为波作用守恒方程：

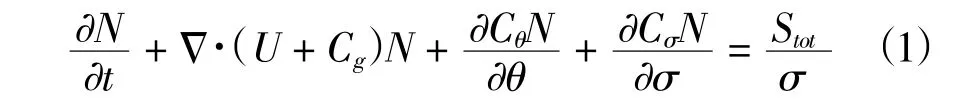
其中N=E/滓，E=籽ga2/2；方程左端第三项和第四项为能作用谱密度N在兹方向和滓方向的传播；右端为源汇项，可以包括波浪破碎，底摩阻等对能量的影响；谱波浪模型中的波浪破碎后的能量耗散模式参考Zheng（2008）构建的模式；而近岸的绕射效应则引入光程函数方程联立来计算：

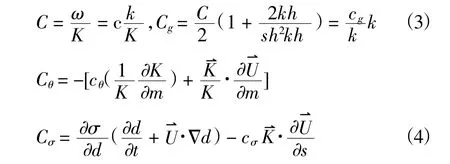
联立方程（1）～（4）得到包含绕射的波浪计算模式，该模式在空间上的离散不受波长的限制，可以用于大范围波流耦合计算。

1.2 三维潮流模型

流场计算基于三维水动力模型FVCOM（Chen，2003），同时引入三维波生时均剩余动量和波浪紊动掺混效应对水体的影响，在坐标系下控制方程如下：

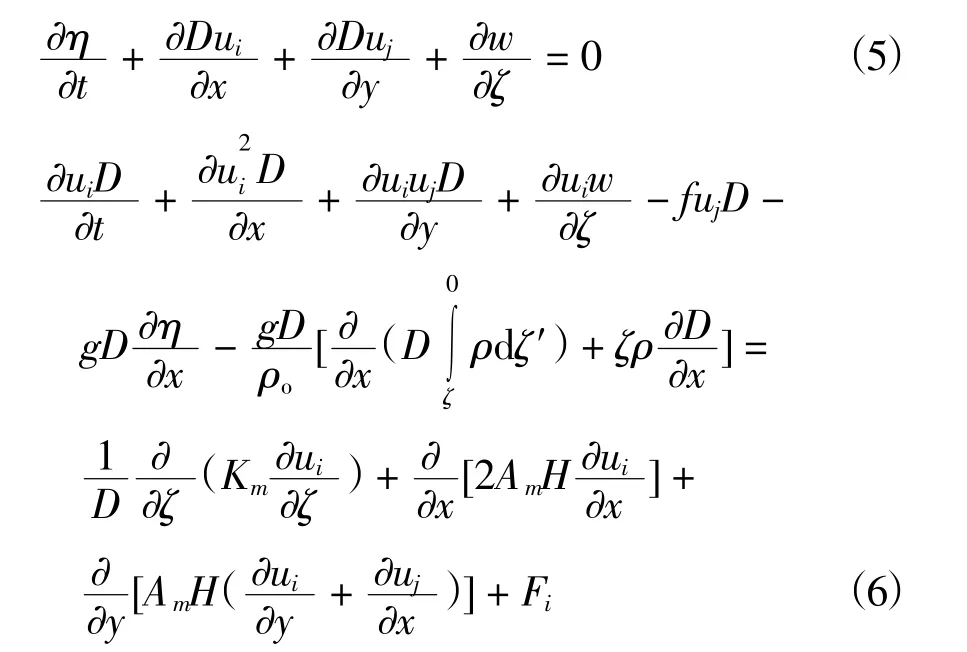
式中：i，j代表x，y方向，灼=（z-浊）/D，Km为波流共存的垂向紊动粘性系数；Am为波流共存的水平紊动粘性系数；Fx和Fy为波浪辐射应力项。对波流共同作用下的紊动系数采用Xia（2003）的方法，分别单独求解水流与波浪引起的紊动系数A和K，并将其线性叠加，表述为：

波浪引起的水平紊动系数Aw计算采用Larson-Kraus公式计算，式中umax为波浪底部质点最大流速，姿为无因次系数；垂向紊动系数采用ЪaЩкИpobp公式，见式（8）。流场引起的水平紊动系数采用Smagorinsky公式计算，见式（9）；垂向紊动系数Km则采用Mellor-Yamada紊流闭合模型计算。

波浪辐射应力项采用Zhang（2004）推导的利用波能E等参数计算，具体形式如下：

1.3 污染物迁移模型

为研究湾内污染物的输移规律，首先利用输移扩散模型研究湾内保守污染物的滞留率，其次采用拉格朗日粒子追踪模型研究湾内污染物的迁移轨迹。输移扩散模型采用滓坐标下的输运方程作为控制方程：

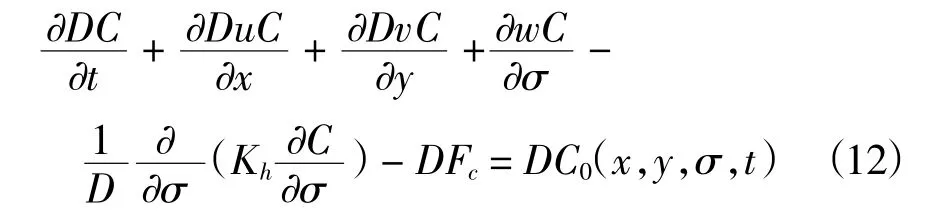
其中：C为任意时刻浓度，C0为初始浓度，Kh为垂向湍流扩散系数，DFc为扩散项。

1.4 离散方法

基于三角形网格，波浪场采用有限体积法对波作用守恒方程进行离散；对光程函数方程采用网格中心格式的有限体积法离散。时间离散采用欧拉向前格式，空间采用格林公式将面积分转为线积分，具体形式如下：

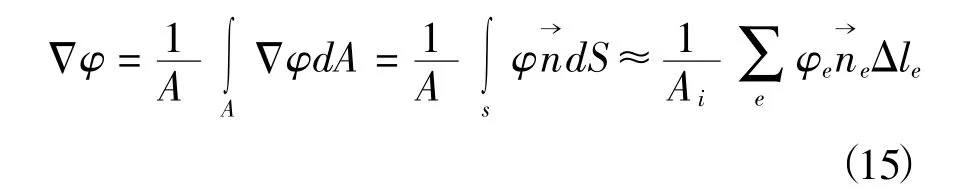
对方程（1）分四步离散求解，空间离散采用单元中心顶点格式的有限体积法在控制体内积分；波谱在频率方向上采用FCT离散方法（Boris，1973）；在传播方向上的离散采用二阶隐身Crank-Nicolson差分方法；源项对波谱的影响采用二阶隐式中心差分离散求解。方程（2）采用网格顶点格式的有限体积法在控制体内积分，空间求导采用将面积分转化为线积分，并将线积分写成各控制边求和的形式，具体离散格式见Wang（2014）的研究。

三维潮流场、输移扩散模型以及粒子追踪模型的控制方程离散见Chen（2003）的研究，而对于辐射应力项同样采用单元中心顶点格式的有限体积法在控制体内积分，同时用格林公式将面积分转换为各控制边上的求和形式，具体形式见公式（16）和（17）。

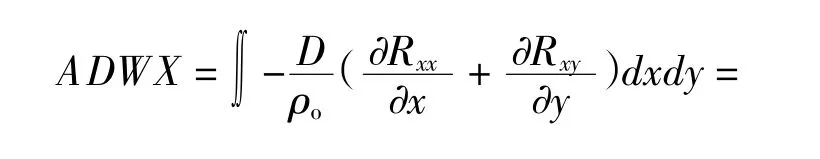
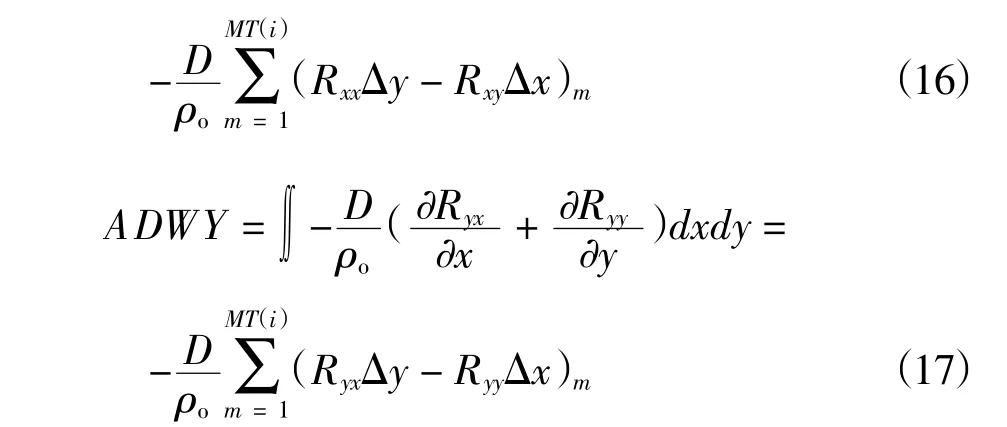
流场和波浪的耦合过程分为，流场和波浪单独计算以及参量相互传递两个过程。其中流场为波浪提供流速和水位参量，而波浪场则为流场提供辐射应力项和紊动系数。流场和波浪场在完成每一步计算后以及下一步计算开始之前进行参量传递，最终实现波流的相互耦合计算。

2 模式的验证及应用

旅顺港地处黄、渤海要冲，港湾内水深1～5 m，湾内水体通过一狭长水道与外海相通，见图1（a）。港湾为几乎全封闭海域，湾内受外海波浪的影响较小；但水道从外海到湾口逐渐变窄，水深逐渐变浅，当外海波浪传至湾口时会发生浅化破碎，进而形成波生流，其对湾口附近流场及污染物的输移均会产生影响。因此研究波浪和潮流共同作用下旅顺港湾内污染物迁移扩散规律十分必要。

2.1 波流耦合的计算及验证

模型计算采用非结构化三角形网格，在湾内区域对网格进行加密，见图1（b）；垂向分10个滓层。空间最小步长为100 m，时间步长为5.0 s。潮流计算从2011-5-25至2011-6-26止，其中包含6月4日的一次大潮过程和6月10日的一次小潮过程；波浪计算一次SE向（大连地区的常见浪向）来浪过程，有效波高为2.5 m，周期为8 s，采用Jonswap谱。

图1 旅顺港水深及计算区域网格图

为了研究波浪及波生流对潮流的影响，先单独计算波浪传播过程。得到全域的波高分布及波生流场分布见图2（a）和（b），从图中看出波浪破碎后会在近岸产生波生流场。由于湾口成喇叭形状，波浪破碎后在湾口两侧形成沿岸流，并在湾口中间形成裂流，进而会对湾口流场以及湾内的水体交换产生影响。

考虑潮流的影响时，先单独计算潮流过程，后在耦合波浪与潮流同时计算。潮流作用下的涨急和落急过程见图3（a）和（b）。从流场图看出，单独潮流作用下，由于旅顺港湾口处老虎尾的挑流作用，在湾内近湾口处形成一逆时针方向的涡，随着潮位的涨落该涡呈周期性变化，其强度在0.30～0.60 m/s变化；湾底由于水深较浅，水动力较弱，流速强度为0.05～0.20 m/s。

波流耦合情况下的流场分布见图4（a）和（b），耦合波浪作用后，波浪破碎后会在浅水区形成沿岸流及裂流等。由于湾口变窄及地形的影响，湾口处存在较大的沿岸流及裂流，其值在0.1～0.25 m/s之间，与潮流场相比波生流的作用范围较小，但量级在近岸基本一致，且由于波生流的作用方向基本不变，其较周期性的潮流对近岸污染物的输运影响可能更大。

计算得到两种情况下的湾内测点潮位和流速过程线对比验证结果见图5；从对比结果可见模型能很好的模拟湾内的水动力变化过程，波浪对潮位的影响较小，可忽略不计；对湾口附近流场（P1点）有明显的影响，但对湾内流场（P2、P3点）影响较小。一般流场的现场观测是在三级海况以下进行的，此时的波高应在1.25 m以下。由于没有现场的波浪观测资料，为获得较好的对比结果，本文入射波的波高为2.5 m，因而计算得到的波流耦合下P1的流速结果较实测值要大。

由于旅顺港湾底有大片低潮时露出水面的浅滩，模式中采用干湿判断来处理漫滩过程，并使用一个最低水深来判断网格点是否参与计算，因此不可避免会造成湾中水体的不守恒，因而模式计算得到的P2和P3点的结果和实测值不是完全吻合。

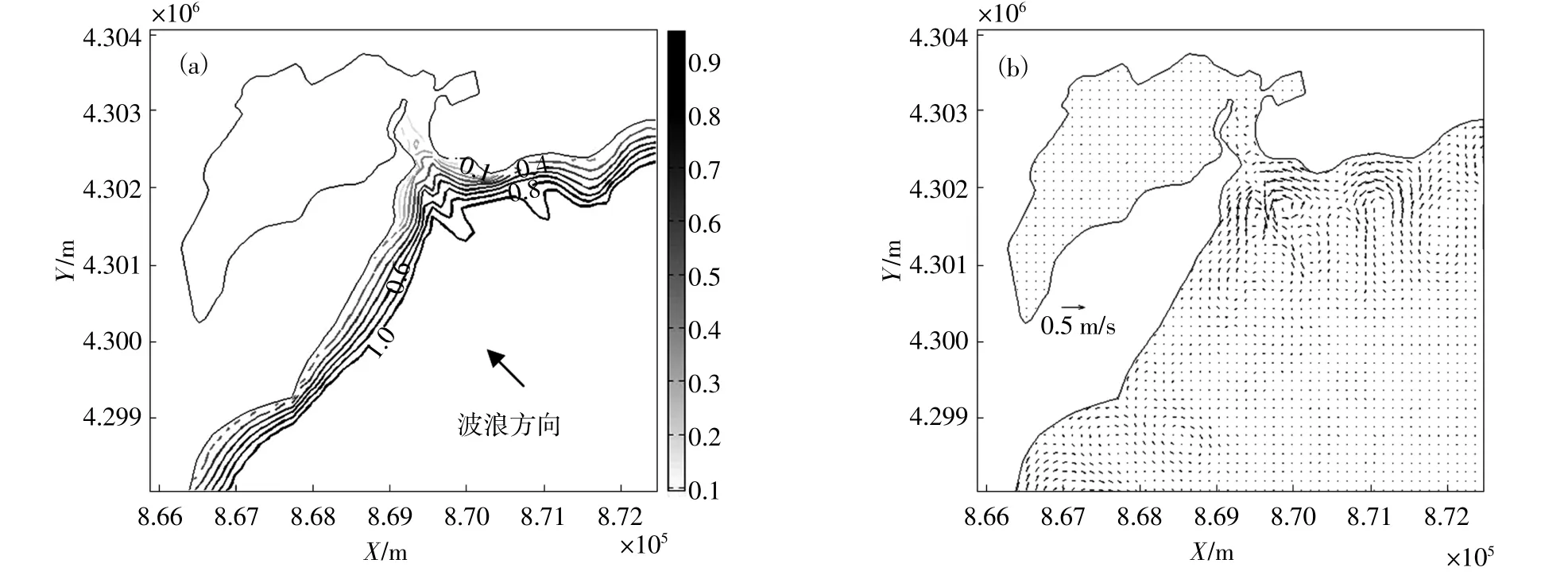
图2 未耦合潮流的全域波高及波生流场分布

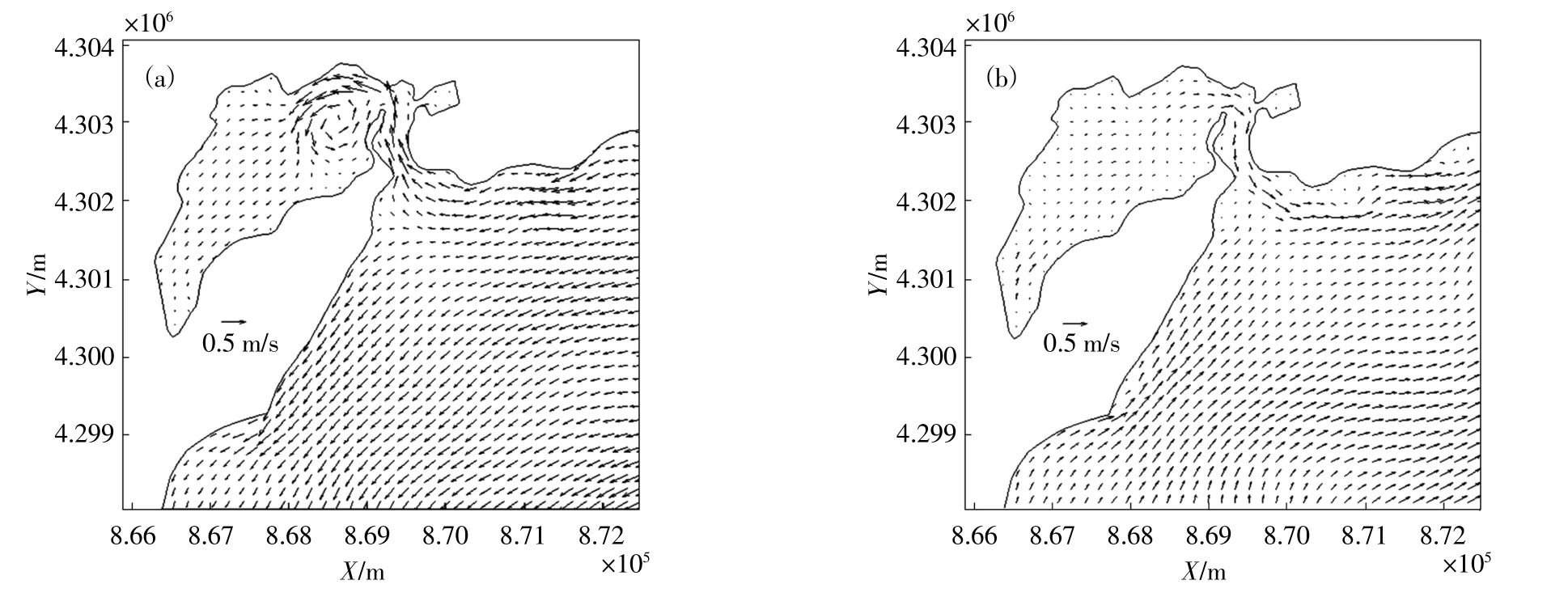
图3 大潮时未耦合波浪场的涨急和落急图

图4 大潮时耦合波浪场后涨急和落急图

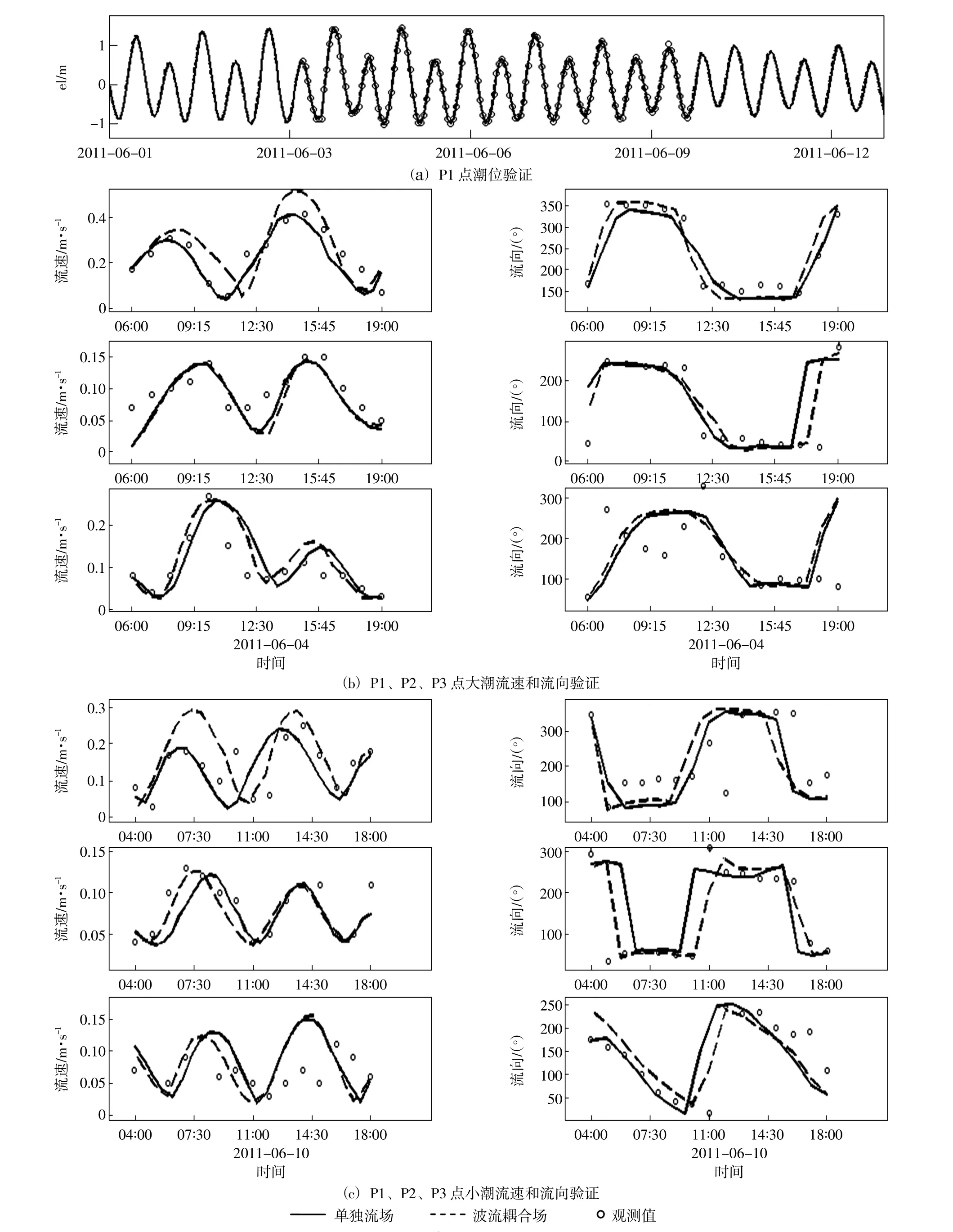
图5 不同站点潮位和流场过程线验证

波浪破碎引起的波面水滚（Zheng，2009）作用会导致表面能量的向岸传递，进而造成波生流的空间分布的变化，但由于本文中波浪破碎的区域水深较陡，波浪破碎过程较快，破碎水滚造成的波生流空间差异较小，且较潮流的作用该差异变化对整体流场影响不大，因此本文中未考虑破碎水滚对波生流空间的影响。

2.2 湾内污染物的输移扩散过程

为研究湾内水体的潮流自净能力，在波流耦合模型的基础上结合拉格朗日粒子追踪模型，从而得到湾内粒子的运动轨迹。在湾内平均展布800个粒子释放点。粒子位置每个小时输出一次，模拟粒子在旅顺港湾内及其附近海域30天（60个潮周期）内的运动。模拟得到粒子在第10、20、30、40以及60个潮周期时的位置变化，如图6。从不同时刻的粒子位置分布可以得到，位于涡内（即湾口附近）的粒子能很快运动出湾外，而湾底的粒子则在湾内滞留时间较长。

经济全球化时代，没有爱国主义，国家就可能会被削弱、被肢解。经济全球化从多方面冲击着民族国家：在经济上，国家之间的经济联系和利益攸关性越发增强，处于弱势地位的发展中国家面临经济主权和安全的巨大挑战；在政治上，国际组织和区域一体化的发展，使民族国家的国家主权受到一定削弱；在文化上，世界上许多国家(尤其是第三世界国家)的民族文化受到了西方国家文化的巨大冲击。

图6 湾内粒子不同时刻位置图

为研究湾内不同污染物排污位置对水体环境的影响，在水动力模块上结合污染物输移扩散模型。在湾内选取2个典型排污点，在单独完成6个潮周期的水动力计算后，分别在湾内每个排污点上释放浓度为1的示踪剂作为初始污染物浓度，污染物连续释放至第20个潮周期后停止，污染物随水体发生迁移和扩散。完成60个潮周期的计算后，得到任一时刻湾内污染物垂向平均浓度分布，其中第30和60个潮周期时刻的污染物浓度见图7。

通过计算Lagrange粒子在湾内的滞留率，以研究波浪作用在湾内粒子输移的影响，波流耦合前后湾内粒子数变化见图8（a）；同时计算不同时刻保守污染物在湾内的滞留率，判断污染物在湾内不同区域排放时对湾内整体水环境的影响，两种情况下污染物在湾内滞留率的变化见图8（b）。

从图8可知，相对于1点，2点释放的保守污染物较难迁移出湾外，主要由于1点靠近湾口且在水动力较强的涡内；而耦合波浪的作用，会削弱潮流对湾内粒子以及保守污染物的迁移能力。

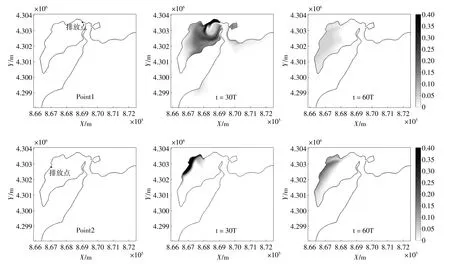
图7 不同时刻湾内示踪剂浓度分布

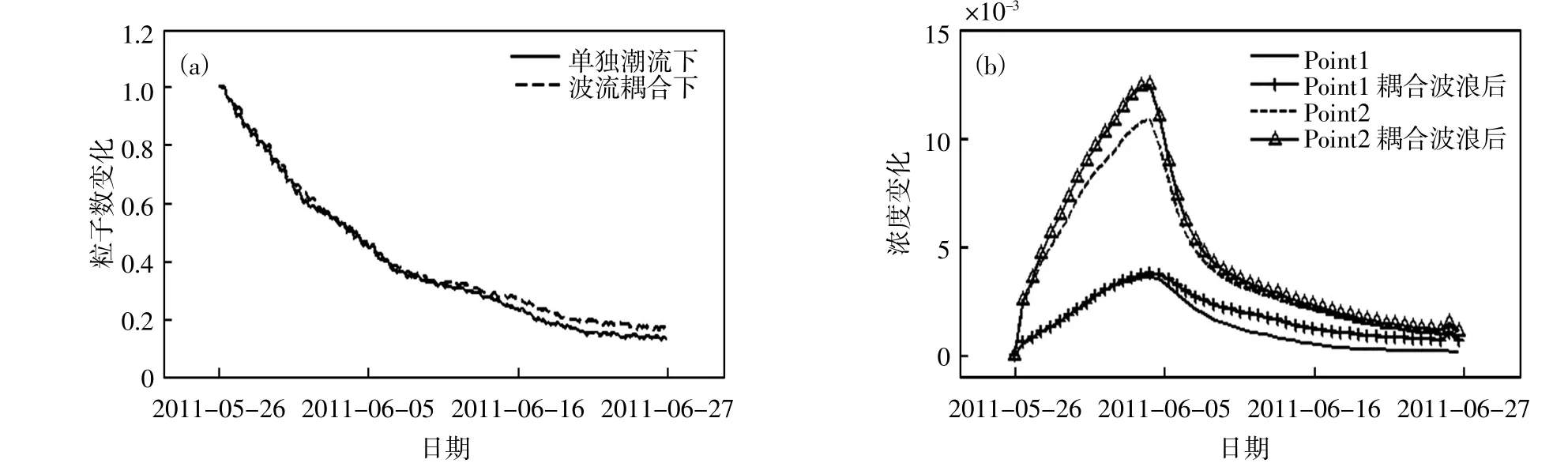
图8 湾内粒子数及示踪剂浓度变化

2.3 新水道对污染物输移的影响

为提高湾内水体的交换能力，在现有湾口潮流通道的基础上，开挖一条新的潮流通道，通道宽100 m、深2 m。模型计算后得到通道开挖后的涨急和落急流场，见图9（a）和（b）。

为了研究新潮流通道对湾内水环境的影响，同时计算了湾内粒子迁移过程以及保守污染物输移过程，计算工况和2.2节中相同，得到第10、30和60个潮周期时刻的粒子位置分布，见图10。图11（a）和（b）分别为新水道开挖前后示踪粒子和保守污染物在湾内的滞留率对比。

从图中可知，新潮流通道开挖会大大缩短湾底附近粒子迁移出湾外的时间，对湾底浅水区域的水体交换能力有显著改善；对分别在1和2号位置排放的保守污染物向外迁移也均有明显的促进作用。

图9 新水道开挖后大潮时的涨急和落急图

图10 工程后的粒子不同时刻位置图

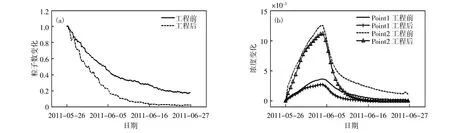
图11 工程前后湾内示踪粒子数及示踪剂浓度变化

3 结语

基于非结构潮流模型及波浪模型，构建了近岸波流耦合下保守污染物的输移扩散研究模型，模拟了旅顺港湾内外的潮流形态、波生流场、保守污染物的迁移扩散过程以及新水道开挖对湾内污染物迁移扩散的影响。主要结论为：

（1）潮流会在湾内近湾口处形成一强度较大的逆时针涡，但湾内中部和底部潮动力较弱；波浪对湾内的影响很小，但SE向波浪破碎会在湾口处形成沿岸流和裂流，波生流场的存在会改变湾口附近潮流场的分布，对湾内流场影响不明显。

（3）新潮流通道的开挖能明显促进湾内污染物的向外输移；对湾内浅水区域的作用较明显，对湾口及湾中部水体也有相应的改善能力。

Boris J P,Book D L,1973.Flux corrected transport玉，SHASTA，a fluid transport algorithm that works.J Comp Phys,11(1):37-39

Chen C,Liu H,Beardsley R C,2003.An unstructured grid,finitevolume,three-dimensional,primitive equations ocean model:Application to coastal ocean and estuaries.J Atm&Oceanic Tech,20(1):159-186.

Doos K,Engqvist A,2007.Assessment of water exchange between a discharge region and the open sea-a comparison of different methodological concepts.Estuarine,Coastal and Shelf Science.74(4):709-721.

Shen J,Wang H V,2007.Determining the age of water and long-term transport timescale of the Chesapeake Bay.Estuarine,Coastal and Shelf Science.74(4):585-598.

Sun T,Tao J H,2005.Experimental and numerical study of waveinduced long-shore currents on a mild slope beach.China Ocean Engineering,19(3):469-484.

Tang J,Shen Y M,Qiu D H,2008.Numerical study of pollutant movement in waves and wave-induced long-shore currents in surf zone.Acta Oceanologica Sinica,27(1):122-131.

Wang P,Zhang N C,2014.A large-scale wave-current coupled module with wave diffraction effect on unstructured mesh.Sci China-Phys Mech Astron,57:1331-1342.

Wei C,Vijay P C,Zeki D,2005.On the modeling of wave-current interaction using the elliptic mild-slope wave equation.Ocean Engineering,32(17):2135-2164.

Wu C S,Liu P L F,1985.Finite element modeling of nonlinear coastal currents.JournalofWaterway,Port,Coastal,andOcean Engineering,111(2):417-432.

Xia H Y,Xia Z W,Zhu L S,2004.Vertical variation in radiation stress and wave-induced current.Coast Eng,51(4):309-321.

Zhang D,2004.Numerical simulation of large-scale wave and currents.Singapore:National University of Singapore.

Zheng J H,Mase H,Demirbilek Z,et al,2008.Implementation and evaluation of alternative wave breaking formulas in a coastal spectral wave model.Ocean Engineering,35(11-12):1090-1101.

Zheng J H,Tang Y,2009.Numerical simulation of spatial lag between wave breaking point and location of maximum wave-induced current.China Ocean Engineering,23(1):59-71.

唐军,魏美芳,2010.非结构化网格下近岸波生流数值模拟.海洋学报,32(6):41-46.

王昆,王年斌,2010.辽东湾海域水体污染物输运的数值模拟.水动力学研究与进展,25(4):493-498.

王平,张宁川,2013.大连湾保守污染物迁移三维模型及应用.海洋通报.32(2):265-274.

张洪生,赵红军,丁平兴,等,2007.非均匀水流水域波浪的传播变形.水力学报,39(3):325-332.

郑金海,Hajime Mase,2008.波流共存场中多向随机波浪传播变形数学模型.水科学进展,19(1):78-83.

Numerical simulation and study of the conservative pollutant migration under wave-current coupling action

WANG Ping1,ZOU Wen-feng2

(1.National Marine Environmental Monitoring Center,Dalian 116023,China；2.CCCC&DLUT Institute of Transportation Technology Co.Ltd,Dalian 116024,China)

Based on the three-dimensional hydrodynamic model,coupled with spectrum wave module,the Lagrangian particle tracking model and convection-diffusion model,a coupled model is established to simulate conservative pollutant migration under coexisting wave-current.The usage of unstructured grid provides great flexibility for simulating the tide,wave and pollutant transport in the area with complex geometries,and the model can simulate the wave-current coupling process in the large-scale area.The tidal current field,wave-induced current,conservative pollutant migration,particle motion and the influence of a new waterway on pollutant migration are simulated and researched by the coupled model.By verification,the results of present model agreed well with the field observed data.The results show that a tidally-induced vortex exists behind the bay mouth,and the wave has little impact in the bay,but wave-induced current will make the flow field change outside the mouth；the self-purification capacity of conservative pollutants in the vortex is better than that in the middle and bottom of the bay,and the water self-purification capacity will be decreased by SE wave action in the bay；the new waterway will strengthen the water self-purification capacity,especially in the bottom of bay.

wave-current coupling;wave-induced current;contaminant migration;Lagrange;numerical simulation

P731.2

A

1001原6932（圆园17）05原园568原10

10.11840/j.issn.1001-6392.2017.05.013

2016-05-12；

2016-07-29

海洋公益性行业科研专项（200905007；201505019）；国家自然科学基金（51709054）。

王平（1988-），助理研究员，主要从事海洋动力学研究，电子邮箱：wping0503@163.com。

邹文峰，硕士。电子邮箱：wfzou@126.com。

（本文编辑：袁泽轶）