考虑裕量损失函数的预测控制新架构
2017-11-01周衍彤罗雄麟
周衍彤 罗雄麟 许 锋
(中国石油大学(北京)地球物理与信息工程学院)
考虑裕量损失函数的预测控制新架构
周衍彤 罗雄麟 许 锋
(中国石油大学(北京)地球物理与信息工程学院)
在常规预测控制性能指标函数的基础上加入一个表征操作变量空间变化情况的裕量损失函数,提出一种考虑裕量损失函数的预测控制新架构,并推导其优化求解过程。同时,通过稳态最优值分析新架构保留操作变量空间的效果,并采用稳态分析在预测控制中加入裕量损失函数对控制效果的影响。最后,通过实例仿真证实了新算法的有效性。
连续搅拌反应器 模型预测控制 裕量损失函数
由于实际的化工过程系统存在慢时变、大滞后、干扰及周期性等不确定因素[1],为保障系统的实际应用与安全性,工艺人员在长周期工艺设计初期通常为变量预留了一定的裕量。在动态操作优化过程中,操作控制会消耗操作变量的可操作空间[2,3],虽然工艺人员已经为操作变量设计了裕量,但是控制人员在进行操作时希望令单次控制中操作变量消耗的空间尽可能地少,不仅可以为长周期过程工艺内以后的控制留下更多的操作空间和余地,将控制的“好处”缓慢地释放,而且可以将操作点控制在工艺裕量限以下,保障生产可靠和安全。预测控制由于其区间控制[4,5]和多变量控制的特点,可以实现在工艺生产操作优化的动态控制过程中减少操作变量的空间损耗。为此,提出一种在常规预测控制性能指标函数中考虑裕量损失函数的预测控制新架构。国内外学者针对预测控制做了大量的研究,有许多通过改进预测控制性能指标函数以改进预测控制性能的研究成果。文献[6,7]和文献[8]分别提出在预测控制的性能指标中引入终端约束来保证预测控制系统的稳定性;文献[9]在常规预测控制性能指标中加入静态目标,在满足基本控制要求的基础上进一步实现系统的经济指标等。
对预测控制中的裕量研究,文献[10]通过在长周期化工过程的动态优化中采用预测控制,为设计变量进行裕量设计;文献[11]研究了先进控制条件下化工过程的操作裕量和控制系统性能之间的关系。上述在预测控制中讨论的裕量,都是研究长周期过程工艺通过动态优化进行裕量设计的。
为了说明在预测控制中考虑裕量损失函数的正确性与科学性,笔者对在预测控制中考虑裕量损失函数的方法论的产生、存在意义及其必然性[12]进行深入剖析。从实际应用角度,深入探讨考虑裕量损失函数的预测控制与常规预测控制相比节省操作变量空间的效果,并分析为了在控制中少消耗操作变量的空间对控制带来的影响。笔者研究了所提方法在预测控制的短周期动态过程中考虑操作裕量的变化情况。
1 裕量损失函数
在化工过程中,对于存在约束的系统,为避免在边界操作点由装置和工艺本身的不确定因素带来的约束破坏性,将操作点移到约束边界内,移动后的操作点与约束边界之间的距离即为裕量[13]。要想实现在单次控制中令操作变量消耗的空间尽可能地少,需要定性表征操作变量消耗空间的情况,为此引入操作裕量的概念。根据裕量的定义,将操作裕量定义为操作变量的操作点与约束边界之间的距离(图1)。当操作变量的操作点与约束边界之间的距离减小时,操作裕量减小,过程可操作空间减少,控制消耗的裕量越多;当操作变量的操作点与约束边界之间的距离增大时,操作裕量增大,过程可操作空间增大,控制消耗的裕量越少。
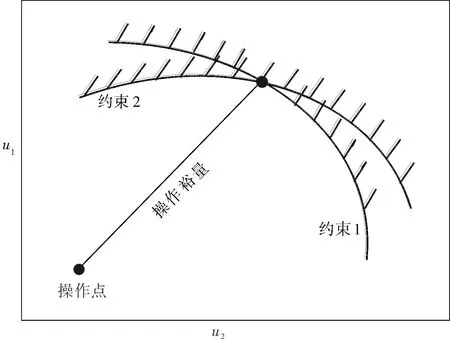
图1 操作裕量示意图
为定量考虑动态控制中操作裕量的变化情况,构建一个表示操作变量操作点u与约束边界之间距离的函数,并定义为裕量损失函数。二范数是具有“长度”概念的函数,通常用来表示两点或向量矩阵之间的直线距离,因此裕量损失函数fML的数学表达式记为:
fML=‖u-uH‖2
式中uH——操作变量的约束上界。
2 考虑裕量损失函数的预测控制
2.1 新架构
常规预测控制是一种基于优化的控制算法,它通过某一性能指标的最优来确定未来的控制作用[14],为了在预测控制的动态过程中实现增大操作裕量并减少控制消耗裕量,在性能指标中加入裕量损失函数改进常规预测控制的结构,最终将优化问题转换为二次规划进行求解。
常规预测控制的性能指标函数通常可以写成二范数的形式:
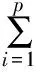
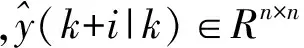
优化求解预测控制的性能指标函数,转换为二次规划的标准形式后,成为求目标函数的极小值,所以在预测控制中引入的裕量损失函数fML_MPC记为负值形式:
fML_MPC=-‖u-uH‖2
因此,考虑裕量损失函数的预测控制的优化性能指标为:
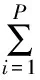
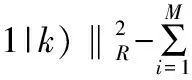
(1)
其中,S≥0为裕量损失函数的权重。
自此,提出考虑裕量损失函数的预测控制(Model Predictive Control with Margin Loss,MLMPC)新架构。
2.2 优化求解过程
假定预测控制采用的线性时不变离散状态空间模型增量化之后的形式如下:
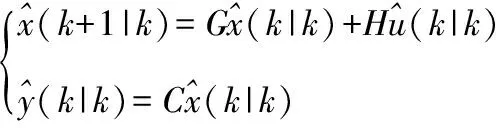
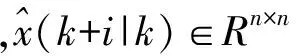
假设系统状态可测,采用矩阵和向量形式表示对输出的预测,即:
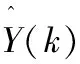
(2)
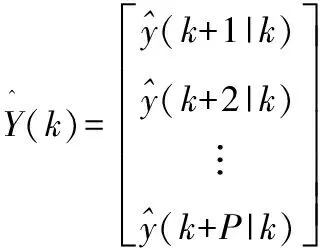
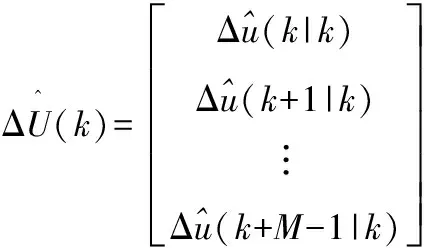
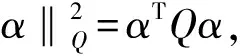
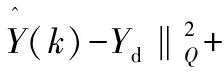
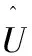
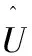
(3)
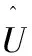
考虑系统关于输入、输入变化量和输出的约束:
umin≤u(k)≤Δumax
Δumin≤Δu(k)≤Δumax
ymin≤y(k)≤ymax
则前述考虑裕量损失函数的预测控制优化问题可最终表述为如下标准二次规划形式:
Ψ=2⎣SΔUTQSΔU+R-ETSE」
Θ=2{-[Yd-Y0(k)]TQSΔU-U1TSE}
d1=[umax-u(k-1),umax-u(k-1),…,umax-u(k-1),-umin+u(k-1),-umin+u(k-1),…,-umin+u(k-1)]T
d2=[Δumax,…,Δumax,-Δumin,…,-Δumin]T
d3=[ymax-y0(k+1),…,ymax-y0(k+P),-ymin+y0(k+1),…,-ymin+y0(k+P)]T
3 控制效果分析
引入常规预测控制的优化问题(4),通过优化求解式(4)可以得到常规预测控制的最优解:
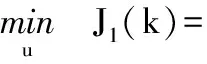
s.t.u=G-1y
(4)
Su≤T
式中G——稳态增益矩阵;
S、T——约束系数矩阵。
同理,求解式(5)可以得到与常规预测控制参数相同的考虑裕量损失函数的预测控制的最优解:
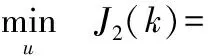
s.t. u=G-1y
(5)
Su≤T
那么有定理1存在。
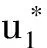
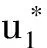
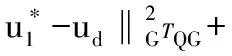
(6)
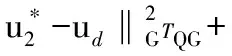
(7)
式(6)和式(7)相加可得:
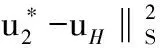
(8)
定理1得证。
4 考虑裕量损失函数的预测控制对控制效果的影响分析
考虑裕量损失函数的预测控制可以在控制的动态过程中实时增大操作裕量,减少单次控制中操作变量消耗的空间,但是与此同时会对被控变量跟踪给定值造成一定的影响。为定量探讨考虑裕量损失函数的预测控制对控制效果的影响,需对考虑裕量损失函数预测控制的稳态情况进行分析。但是,对于存在约束的系统,由于约束的存在难以求解解析解,导致针对控制系统进行稳态分析比较困难。然而,对于同一个控制系统,在无约束情况下的稳定性是在相同控制参数下有约束控制系统稳定的必要条件[15]。同时,在存在约束的预测控制中考虑裕量,通常都会使过程在约束可行域内运行。因此,为了分析考虑裕量损失函数预测控制的稳态情况,可以分析在无约束条件下控制系统的闭环特性,将得到的最优控制作用带入闭环方程中,并判断稳态解的情况。
当被控过程的离散状态空间模型为:
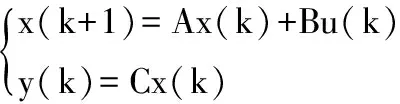
(9)
其中,系统状态变量x(k)∈Rn×n,系统输入变量u(k)∈Rm×m,系统输出变量y(k)∈Rr×r;系统状态矩阵A∈Rn×n、输入矩阵B∈Rn×m、输出矩阵C∈Rr×m。
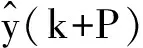
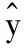
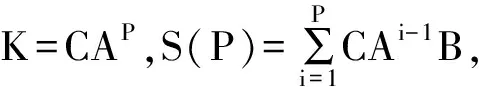
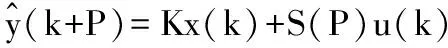
(10)
为了便于分析最终输出达到稳态的跟踪效果,将裕量损失函数用输出形式表示为:
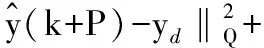
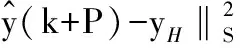
(11)
其中,yH为操作变量约束上界对应的输出变量的值,S′为输出对应的裕量损失函数的权重。由于Δu(k)=u(k)-u(k-1),将式(10)代入式(11),有:
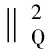
=const+uT(k)ST(P)QS(P)u(k)+2uT(k)ST(QP)Kx(k)-yd)+uT(k)Ru(k)-
2uT(k)Ru(k-1)-uT(k)ST(P)S′S(P)u(k)-2uT(k)ST(P)S′(Kx(k)-yH)
则有:
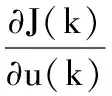
2ST(P)S′(Kx(k)-yH)=0
得到控制最优值,并进行z变换可得:
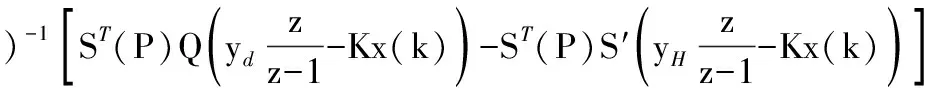
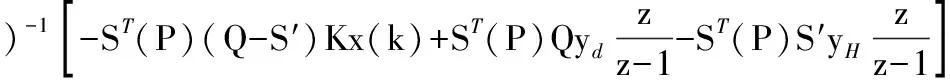
(12)
假设实际过程也遵循式(9),则对式(9)做z变换,有:
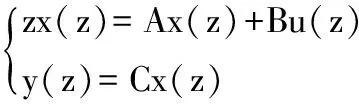
(13)
将式(12)代入式(13),可得:
y(z)=C[zI-A+B(ST(P)QS(P)+R-Rz-1-ST(P)S′S(P))-1ST(P)(Q-S′)K]-1·
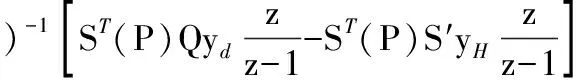
(14)
为判断稳态情况,对式(14)使用终值定理并进行推导:
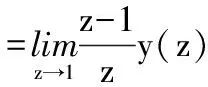
=C[I-A+B(ST(P)QS(P)-ST(P)S′S(P))-1(ST(P)(Q-S′)K]-1·
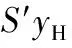
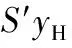
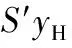
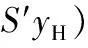
(15)
其中,Gm(z)表示模型的传递函数,则有C(I-A)-1B=Gm(1)。由式(15)可得:
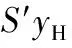
(16)
矩阵(Q-S′)非奇异是输出变量存在稳态解的必要条件。由式(16)可以看出,输出变量的稳态值为输出期望值yd与工艺裕量值yH之间的函数。因此,在考虑裕量损失函数的预测控制中,当权重Q和S′都不趋近于零时,输出的稳态值为输出期望值与操作变量约束上界对应的输出变量的值之间的函数,不能准确无误地跟踪期望值,会有一定的损失。然而,预测控制区间的控制思想可以令被控变量跟踪期望值在一定范围内即可满足控制。因此,控制人员在采用考虑裕量损失函数的预测控制进行控制时,需要合理选择裕量损失函数的权重,在实现减少单次控制中操作变量消耗空间的同时,要确保被控变量在给定的区间范围内。
5 仿真与示例
为验证笔者所提方法的正确性,采用文献[17]中的非等温连续搅拌反应器系统(CSTR)进行仿真分析。其中y1、y2分别表示反应器的浓度与温度,u1、u2分别表示进料浓度和冷却液流量。
其线性离散状态空间模型如下:
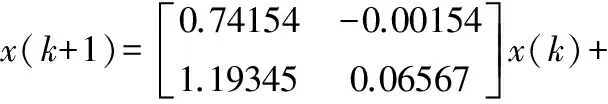
(17)
s.t. -1.5≤u1≤6,-1.5≤u2≤2
-1≤y1≤3,-1≤y2≤2
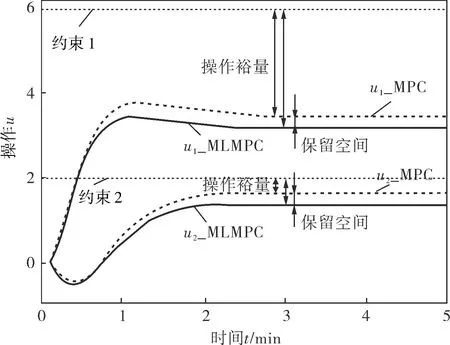
a. 操作变量的响应
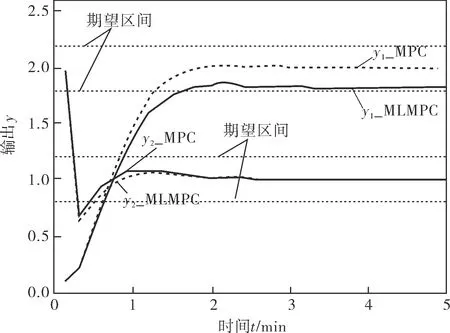
b. 输出变量的响应
6 结束语
通过在常规预测控制的性能指标函数中加入一个能够表示操作裕量变化情况的裕量损失函数,构建了考虑裕量损失函数的预测控制新架构,推导了考虑裕量损失函数的预测控制的优化求解过程,并通过稳态最优解分析了考虑裕量损失函数的预测控制保留操作变量空间的效果,同时分析了在预测控制中考虑裕量损失函数对控制效果的影响。考虑裕量损失函数的预测控制可以在控制的短周期动态控制过程中实时地实现保留操作变量的空间,不仅可以有效缓解边界效应,保障装置和生产的安全性,同时可以令控制的“好处”缓慢释放,为后续的操作优化留出更多的空间和余地。
[1] 何伟,鲁明,李国强,等.SNCR脱硝系统的广义预测控制[J].石油化工自动化,2016,52(1):38~41.
[2] Xu F,Jiang H R,Wang R,et al.Influence of Design Margin on Operation Optimization and Control Performance of Chemical Processes[J].Chinese Journal of Chemical Engineering,2014,22(1):51~58.
[3] 罗雄麟,许锋.过程控制与工艺设计一体化:催化裂化装置动态机理建模与控制分析设计[M].北京:科学出版社,2008.
[4] 罗雄麟,周晓龙,王书斌.输入变量关联约束对约束优化控制的影响特性分析[J].自动化学报,2012,39(5):679~689.
[5] 左信,袁璞.区域预估控制初探·工业过程模型化及控制[M].广州:华南理工大学出版社,1992.
[6] Kwon W H,Pearson A E.A Modified Quadratic Cost Problem and Feedback Stabilization of a Linear System[J].IEEE Trans Automat Control,1977,22(5):838~842.
[7] Kwon W H,Pearson A E.On Feedback Stabilization of Time-varying Discrete Linear Systems[J].IEEE Trans Automat Control,1993,38(10):1512~1516.
[8] Michalska H,Mayne D Q.Robust Receding Horizon Control of Constrained Nonlinear Systems[J].IEEE Transactions on Automatic Control,1993,38(11):1623~1633.
[9] 萧明波,钱积新.预测控制中静态目标的实现[J].控制理论与应用,1997,14(3):313~317.
[10] Sanchez-Sanchez K B,Ricardez-Sandoval L A.Simultaneous Design and Control under Uncertainty Using Model Predictive Control[J].Industrial & Engineering Chemistry Research,2013,52(13):4815~4833.
[11] 许锋,罗雄麟.先进控制条件下化工过程操作裕量与控制性能分析[J].化工学报,2012,63(3):881~886.
[12] 罗雄麟,周衍彤.预测控制的哲学思想分析及其新架构的提出[J].化工进展,2017,36(3):783~790.
[13] Narraway L T,Perkins J D,Barton G W.Interaction between Ptocess Design and Process Control:Economic Analysis of Process Dynamics[J].Journal of Process Control,1991,1(5):243~250.
[14] 席裕庚.预测控制[M].北京:国防工业出版社,1993.
[15] 袁璞.生产过程动态数学模式及其在线应用[M].北京:中国石化出版社,1994.
[16] 袁璞.单值预估控制[J].中国石油大学学报(自然科学版),1992,16(5):100~109.
[17] Sanchez-Sanchez K B,Ricardez-Sandoval L A.Simultaneous Design and Control under Uncertainty Using Model Predictive Control[J].Industrial & Engineering Chemistry Research,2013,52(13):4815~4833.
NewFrameworkofModelPredictiveControlConsideringMarginLossFunction
ZHOU Yan-tong, LUO Xiong-lin, XU Feng
(CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum)
Basing on the performance index function of conventional predictive control, a margin loss function which representing the space variation of operating variables was added; and a new framework of model predictive control algorithm which considers margin loss function(MLMPC) was proposed and its optimization solution was derived. At the same time, having the steady optimal value used to analyze the effects of saving the space of operating variables and that of adding margin loss function to the predictive control. Finally, an example simulation is given to illustrate the effectiveness of this new algorithm.
continuously-stirred reactor, model predictive control, margin loss function
TQ021.8;TP273
A
1000-3932(2017)09-0823-07
2017-03-15,
2017-06-19)
周衍彤(1991-),硕士研究生,从事过程控制的研究。
联系人罗雄麟(1963-),教授,从事控制理论与过程控制、化工系统工程及机器学习等的研究,luoxl@cup.edu.cn。
