这个三角形是等腰直角三角形吗？

南京市金陵中学仙林分校中学部九（11）班 江博熠

这个三角形是等腰直角三角形吗？

南京市金陵中学仙林分校中学部九（11）班 江博熠

在学习轴对称图形的时候，老师跟我们讲了如何在一个等腰直角三角形内构造一个新的等腰直角三角形，我听完很感兴趣.于是我也构思了一个等腰三角形问题，但却无法证明，莫非我构思的新三角形不是等腰直角的？我静下心来，想到老师曾说过，要证明结论不成立，正面证明比较困难，往往要用到反证法.所以我决定尝试一下.

首先，我把问题又重新梳理了一遍：

如图1，在直角△ABC中，AB＝AC，D为BC的中点，且P为CD中点.EP∥AC，作PE的垂直平分线QO.那么△EQP是等腰直角三角形吗？如果是，请证明.

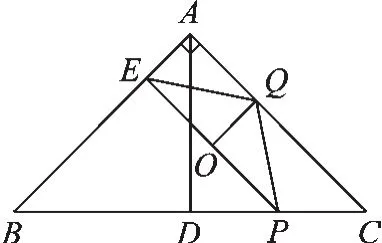
图1

第一步：证明△EQP是等腰三角形.∵QO垂直平分EP，∴QE＝QP.

第二步：过点O作BC平行线FG交两直角边于F、G（如图2），由于EP//AC，易证△EFO、△QOG、△AFG均为等腰直角三角形.

第三步：如图2.

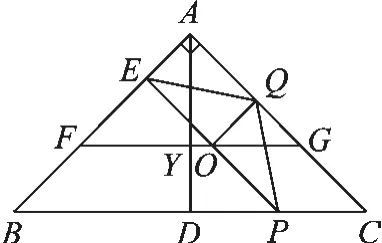
图2

①设AD与FG交于Y点，假如△PQE为等腰直角三角形，那么∠QEO=45°，又因为 QO⊥PE，∴∠EQO=45°,∴∠OEQ=∠OQE=45°，OQ=OE.

②由于∠AEF 为平角，可知：∠AEQ=45°，∵∠BAC=90°，∴∠AQE=45°，所以∠AEQ=∠AQE=45°,因此AE=AQ.

③根据全等的证明容易知道，△EFO、△QOG、△AEQ、△OEQ都是等腰直角三角形且彼此全等.∴FO=GO,也就是说点O和点Y重合.

第四步：由于Y点与O点重合（如图3），所以△OPD为等腰直角三角形.因为点P为CD中点，设PC=DP=1；由于 PE//AC，∴∠OPD=∠C=45°；易知△ACD、△ODP均为等腰直角三角形，所以AD=CD=2，OD=AO=1.

第五步：如图3，在△AEO中，EO＜AO，∴EO＜1.同时在△ODP中，OP＞OD，∴OP＞1.

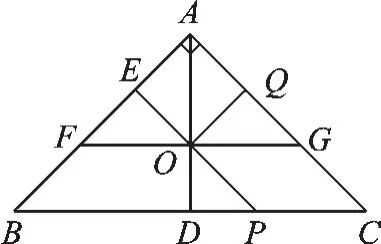
图3

所以OP＞1＞OE，因此点O不是线段PE的中点，和问题的条件矛盾.

教师点评：江博熠同学构思了如图的一个等腰△EQP，但是△EQP是不是直角的呢？他经过长时间的思考没证明出来，于是他改变主意：莫非△EQP不是等腰直角三角形吧！要证明结论不成立，正面证明比较困难，我们往往要用到反证法，江同学的这个思路我们要学习.江博熠同学刚开始思考的时候有不少漏洞，但他能静下心来，把条件梳理清楚，用理性的思考解决了问题.他的经历也告诉我们：思想和方法往往不是一蹴而就的，而是在深思熟虑之后才能够逐步产生.

（指导教师：郝四柱）