RCS测试中的低散射载体设计及仿真分析

梁 爽，刘庆杰，聂 暾，郭 文，张 斌

(成都飞机工业(集团)有限责任公司技术中心，成都 610092)

RCS测试中的低散射载体设计及仿真分析

梁 爽，刘庆杰，聂 暾，郭 文，张 斌

(成都飞机工业(集团)有限责任公司技术中心，成都 610092)

在雷达散射截面(RCS)测试中，低散射载体的设计结果取决于被测目标的RCS量级;为进行细节性隐身设计，获得台阶与缝隙排除载体干扰后的RCS水平，提出一种在台阶与缝隙RCS测试中的低散射载体设计方法;采用多层快速多极子算法，对低散射载体相邻曲面连接方式、台阶与缝隙在载体上的位置、前缘尖削度、倒圆半径对散射特性的影响进行仿真分析;仿真计算结果表明，控制载体表面曲率的变化、加大前缘尖削度、减小拼接曲面倒圆半径能有效降低载体前向散射水平，由于载体曲面一侧的散射水平低于平面一侧散射水平，台阶与缝隙特征应位于曲面上；对RCS测试中低散射载体设计具有指导意义。

雷达散射截面；多层快速多极子算法；低散射载体；电磁散射；隐身设计

0 引言

利用RCS减缩技术可有效降低飞机被雷达探测的概率，降低飞机的敏感性，从而提高飞机的生存力[1]。在隐身飞机研制过程中，需进行大量的室内和外场RCS测试，以进行隐身部件参数的选择和仿真计算结果的验证，如由于制造工艺的限制和使用维护要求，飞行器表面存在大量的缝隙和台阶，需通过大量的隐身测试对缝隙宽度和台阶高度等参数进行选择。飞行器各隐身部件的尺寸一般在1～5 m之间，若将其用于RCS测试，一方面由于尺寸大于一般暗室的静区尺寸而无法测试，另一方面部件的RCS可能大于预测试材料或细节特征的RCS，从而导致预测试材料或细节特征的RCS堙没于部件RCS之中而无法体现[2]，如前述的台阶和缝隙属于弱散射源，采用常规的隐身部件对其进行测试时，台阶和缝隙带来的RCS贡献便体现不出。设计低散射载体是最有效的解决上述问题的方法，将预测试材料或细节特征结构安装于低散射载体之上，由于低散射载体的散射水平低于被测目标1～2个量级，从而可体现出被测目标的RCS，同时也减小了测试目标的体积，便于测试时安装定位和降低制造成本。

文献[3]设计钻石型低散射载体，用于测试螺钉、铆钉、缝隙等电磁缺陷对其RCS的影响。文献[4]采用金属平板载体，通过RCS测试分析，得到了缝隙电磁散射随缝隙宽度、间距的变化规律和极化特性。文献[5]从理论上分析了缝隙的后向散射规律，并设计准菱形平板载体，进行不同几何参数的台阶和缝隙的RCS测试。文献[6]设计了分析倾斜双垂尾电磁散射规律的低散射载体，用于分析尾翼不同参数对其RCS的影响。

采用高精度快速RCS仿真分析算法，对测试台阶与缝隙的不同几何参数的低散射载体进行RCS仿真计算分析，总结低散射载体的设计方法及散射规律。

1 仿真算法选择

低散射载体(也称为低RCS载体)是用于RCS测试时装载测试目标或测试特征，并具有低于被测目标或特征1～2散射量级的一类载体。在设计低散射载体时，需要进行大量的仿真分析，使设计的载体具有较低的散射水平，因此，对仿真算法的计算速度和精度具有较高的要求。

高频近似方法都是标量波方程典型解的应用，具有计算效率高的优点，但由于其进行了一些近似处理(远场近似、切平面近似)[7]，不能精确模拟目标的表面电流，常用于进行散射水平较高的目标RCS预估，对散射水平较低的一类目标其结果会与真实值之间存在较大的误差。

常规的积分方程法(如矩量法)作为一种严格的数值方法，具有计算结果精度高的优点，但计算量大导致其计算效率较低，且收敛性差，长期以来都仅仅用于简单外形目标的RCS计算分析[8]。

采用电场积分方程和磁场积分方程组合的混合场积分方程[9]：

-an×n×Ei(r)+(1-a)ηn×Hi(r)

式中,L(J)=-Es，Es为散射电场强度；K(J)为表达式J(r)×G在S外表面去极点区域后的主值积分；n为S外表面单位外法矢；J为电流强度；Ei(r)为入射电场强度；Hi(r)为入射磁场强度；r为原点到计算点的距离；α、η为系数。

利用多层快速多极子方法[10-13]，将上述积分方程转化为矩阵方程，将传统矩量法O(N2)量级的计算复杂度降至O(NlogN)量级，相应O(N2)量级的存储量降至O(N)量级，在保证计算精度的同时大大降低了计算量和存储量。

低散射载体由于其散射水平较低且外形通常不能用简单的曲面方程加以描述，在设计过程中对其RCS的预估采用多层快速多极子方法，在确保仿真计算精度的同时提高仿真效率。

2 仿真模型及流程

2.1 仿真模型及状态定义

台阶和缝隙是隐身飞机上普遍存在的一类弱散射源，单个台阶和缝隙对全机RCS的影响会堙没于全机各强散射源当中，但全机上存在的若干台阶和缝隙对整机RCS的影响却不可忽视，因此需设计低散射载体，用于台阶和缝隙散射规律及RCS减缩措施的研究。

设计的测试台阶与缝隙特征的低散射载体是一个由平面与曲面组成的半枣核状流线体，如图1所示。前端及后端较尖锐，用于减小入射波正对前向及后向入射时一定角域内的镜面散射和行波散射。外形扁平，减小侧向散射峰值。载体长度1 600 mm，宽度720 mm，高度170 mm，关于通过横向对缝和纵向对缝的平面对称。

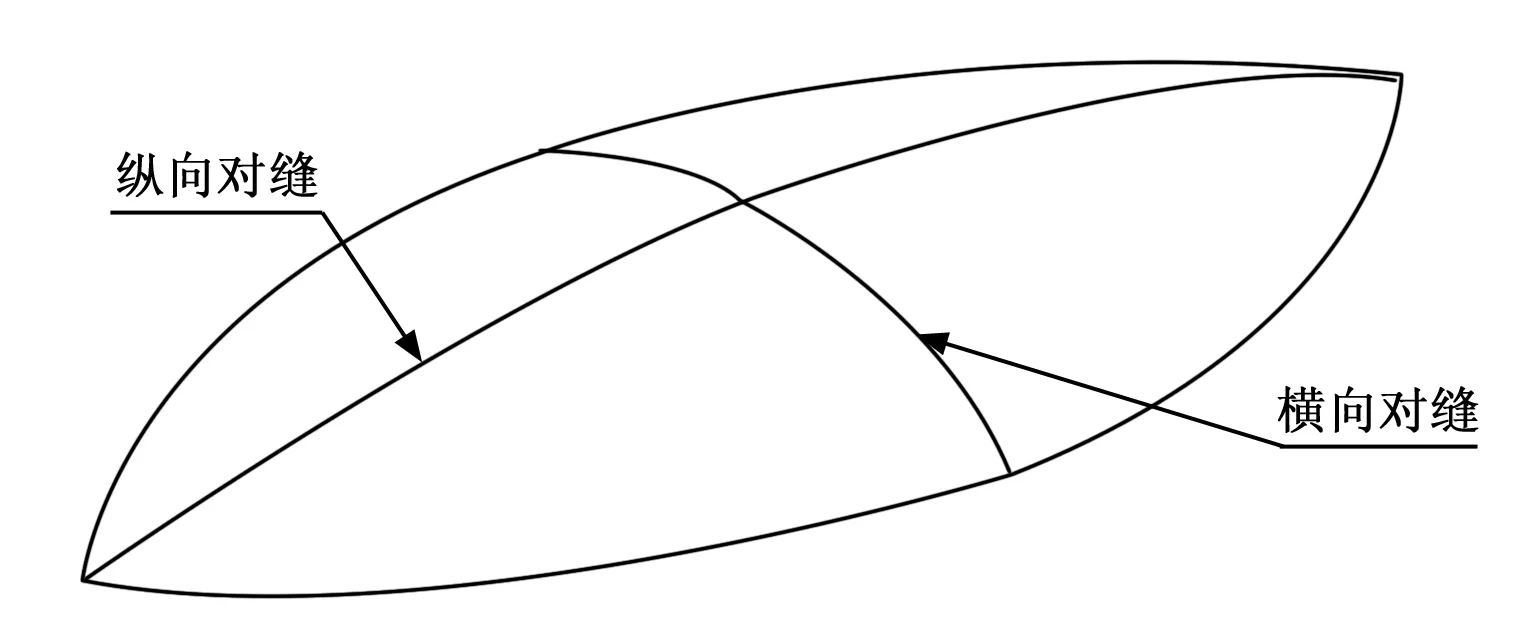
图1 低散射载体外形

仿真计算状态定义如图2所示。其中方位角在载体的平面内定义，规定电磁波沿着载体前向垂直入射为0°方向，沿着载体左右两侧入射分别为90°和-90°方向。俯仰角在载体纵向对称面内定义，规定电磁波沿着载体前向垂直入射为0°方向，沿着曲面一侧法向入射为-90°方向，沿着平面一侧法向入射为90°方向。

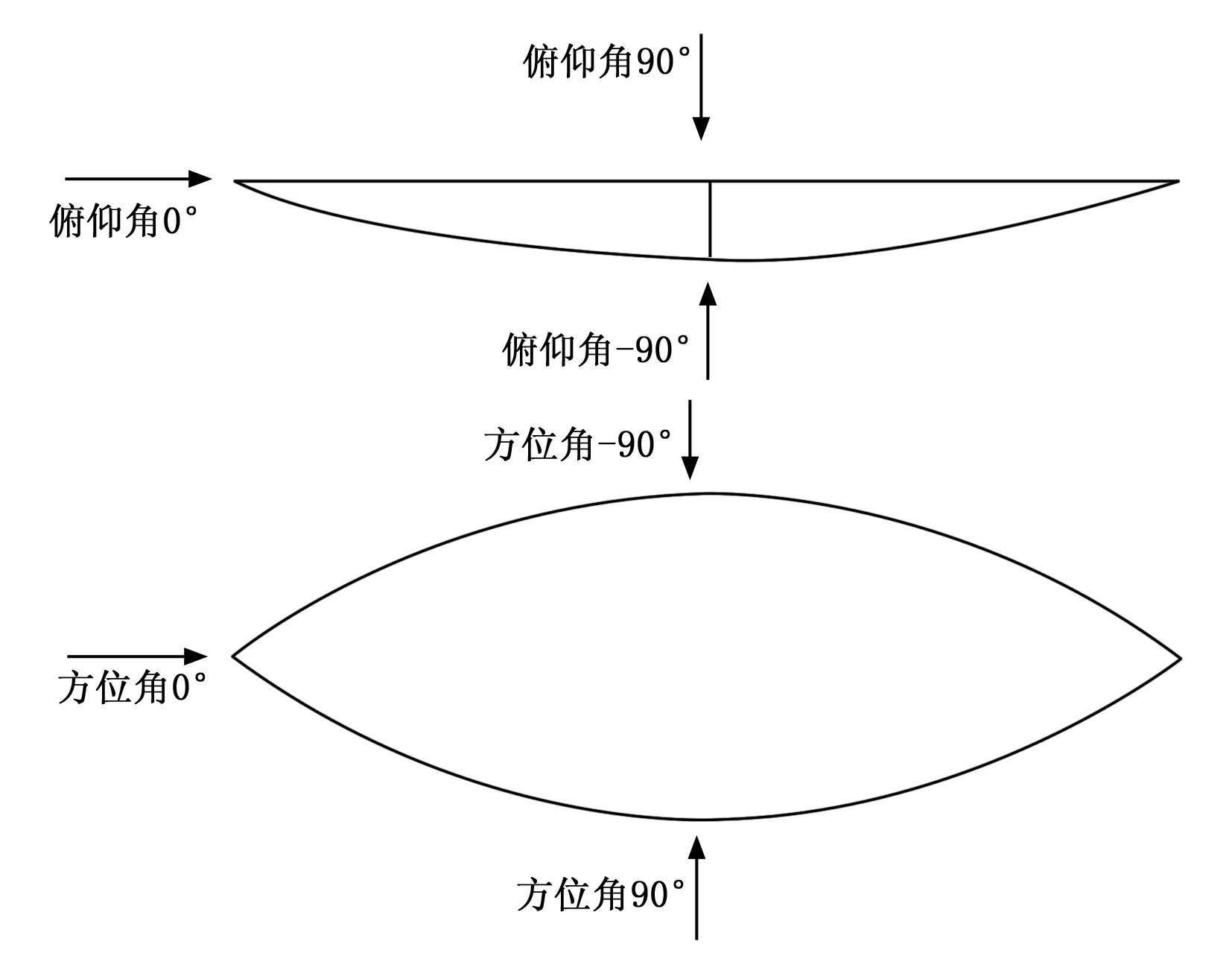
图2 仿真计算状态

由于低散射载体的电尺寸位于高频区时其表面细节才会对RCS造成影响以及此时即使在较小的角度范围内RCS曲线也会有较强的振荡，入射波频率设置为X频段，方位角和俯仰角步长取较小值0.1°，以捕捉细微的入射角度变化对载体RCS的影响。极化方式的定义为当电场方向位于方位角平面内时为水平极化，电场方向垂直于方位角平面时为垂直极化。

2.2 仿真流程

仿真计算流程如图3所示。首先是利用CAD软件对低散射载体进行几何建模，然后用网格剖分软件将其剖分为三角面元网格，并对网格质量(纵横比、内角、最长边/最短边比值、法向等)进行检查与优化，对达不到质量要求的网格进行重新剖分，再设置仿真参数(频率、极化、姿态角、单站求解、双站求解等)，开始仿真计算和后处理，为加速迭代过程，采用混合基的积分方程。当设计的载体满足预期的散射量级要求时，结束仿真计算，否则修改CAD模型，重新开始仿真流程，直到低散射载体的散射水平满足预期的散射量级要求为止。

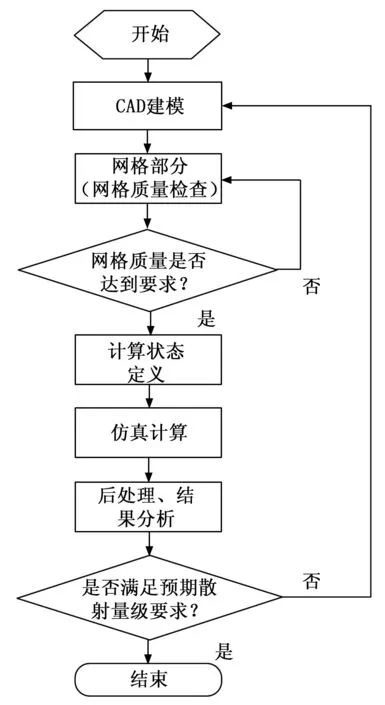
图3 仿真计算流程

3 仿真结果分析

3.1 相邻曲面连接方式对载体散射特性的影响

低散射载体在外形几何设计时已消除大部分入射角度下的二面角、镜面反射等强散射源，因此需着重对弱散射源进行减缩。当入射电磁波在机体表面激起的电流传导到台阶与对缝时，由于电不连续会导致表面电流传导形成阻碍，形成新的弱散射源。与纵向对缝相比，飞行器表面横向对缝激起的后向散射峰值会反射到飞行器的前向，对其前向RCS影响较大，因此分别将图1所示载体相邻曲面横向对缝设计为相切连续和曲率连续，研究曲面之间不同连接方式对散射特性的影响。由于飞行器表面台阶与缝隙等电磁缺陷主要对水平极化下的RCS贡献较大[2]，因此只仿真计算了水平极化下不同连续性特征的RCS，见图4。

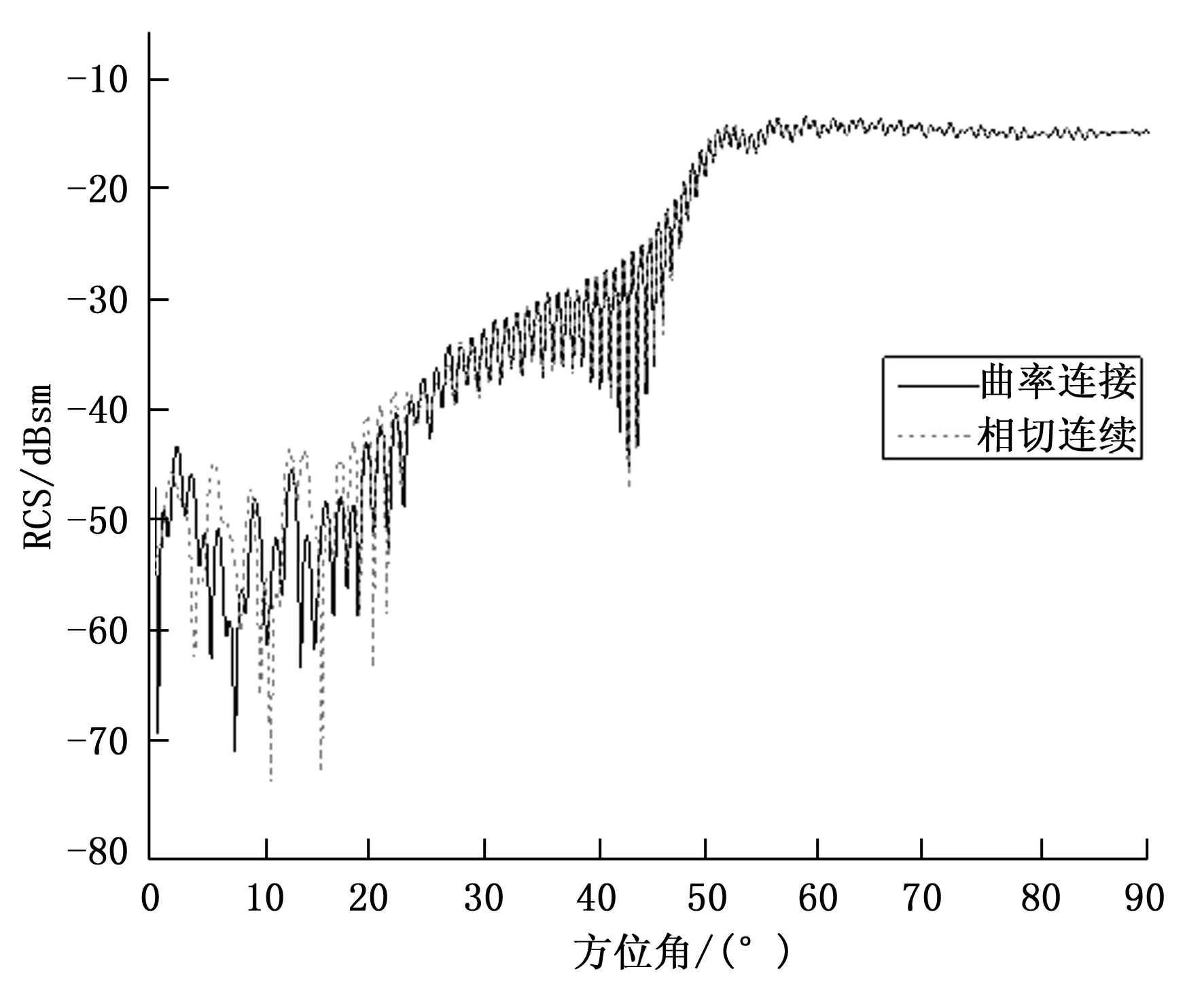
图4 不同曲面连接方式对低散射载体散射特性的影响(水平极化)

通过对图4中数据进行分析，由于采取了外形隐身设计措施，设计的低散射载体在头向0～30°方位角范围内RCS低于-30 dBsm，在0～20°方位角范围内RCS更是低于-40 dBsm，处于较低的散射水平。在0～30°方位角范围，不同曲面连接方式RCS差异较大，横向对缝为相切连续的载体在多数方位角下的散射峰值高于横向对缝为曲率连续的载体，在30～90°方位角范围内，由于不同连接方式造成的电不连续散射源的散射主要集中在前向角域内，此时占主导地位的散射源为曲面的漫反射，因此两者基本吻合。通过均值计算，横向对缝为相切连续的载体在头向0～30°方位角范围内RCS均值为0.000068 m2，横向对缝为曲率连续的载体在0～30°方位角范围内RCS均值为0.000065 m2，优于横向对缝为相切连续的载体。同时，不同曲面连接方式对载体RCS的影响主要体现在前向一定的角域内，在角域外(侧向)影响不大。

3.2 台阶与缝隙在载体上位置

将低散射载体设计成平面加曲面构成的形式，主要考虑的因素是在微波暗室测试时平面易于在转台上安装、定位以及精确控制测试角度。平面与曲面具有不同的RCS特性，需在俯仰方向内对载体进行RCS仿真，以便确定台阶与缝隙在载体上的位置。图5是载体俯仰方向的RCS散射特性，其中-90°俯仰角对应于入射波垂直于曲面最高点法线入射，90°俯仰角对应于入射波垂直平面法向入射，-90～0°俯仰角范围对应于入射波照射到曲面上，0～90°俯仰角范围对应于入射波照射到平面上。

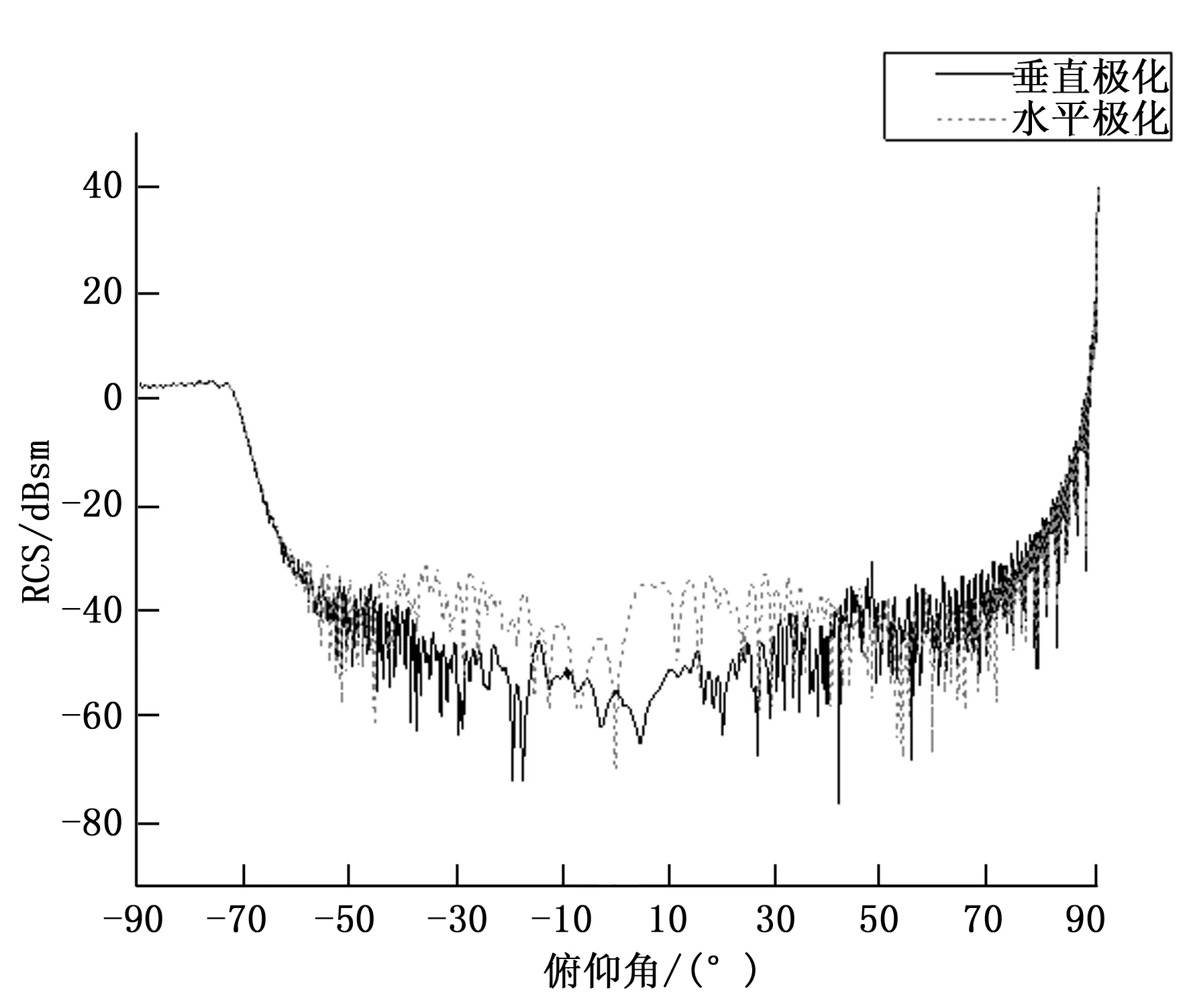
图5 载体上曲面与平面RCS散射特性(水平与垂直极化)

通过对图5中数据进行分析，在垂直平面和曲面的法向入射的情况下，平面的峰值较大，水平极化和垂直极化下达到30 dBsm左右，这是金属平板产生的强镜面反射回波，在入射波偏离垂直入射方向后，RCS峰值迅速下降到较低水平：在70°俯仰角时下降到-30 dBsm；曲面的散射峰值在水平极化和垂直极化下为0 dBsm左右，在入射波偏离垂直入射方向后，RCS峰值仍在一定俯仰角(-90～-70°)范围内维持在0 dBsm的散射水平，这是由于曲面散射具有散射峰值不高(较平面的镜面反射而言)，但在大部分方位角范围内由于漫反射其RCS维持在一定的散射水平的特点决定的。

由于当雷达波以掠入射(俯仰角-10°～10°范围)角度照射到飞行器上时，会激起缝隙和台阶造成的RCS激增，因此应重点关注掠入射时低散射载体上平面与曲面的不同散射特性。由图5可见，掠入射时水平极化下平面的散射水平大于曲面的散射水平，垂直极化下两者的散射水平相当。经过均值计算，掠入射时水平极化下曲面一侧(对应俯仰角-10～0°)的均值为0.00001717 m2，平面一侧(对应俯仰角0～10°)的均值为0.00024 m2，较曲面散射大一个量级，垂直极化下曲面一侧(对应俯仰角-10～0°)的均值为0.00000405 m2，平面一侧(对应俯仰角0～10°)的均值为0.000002978 m2，两者处于同一个量级。台阶、缝隙应处于曲面一侧，以更好地体现出台阶、缝隙取不同几何参数值时对载体RCS的影响，同时也更符合飞行器表面为曲面构成的工程实际。

3.3 前缘尖削度对散射的影响

载体前缘尖削度，定义为在载体前缘点与载体曲线相切直线的后掠角(见图6)。载体前缘尖削度对前向散射的影响，类似于机翼后掠角对飞机前向RCS的影响，主要用于将前向RCS散射峰值偏移到前向一定散射角域外，以降低前向散射水平。为找出载体前缘尖削角度对其散射水平的影响，仿真计算了水平极化和垂直极化下典型尖削角度(分别为45°和35°)的载体RCS特性曲线，如图7所示。

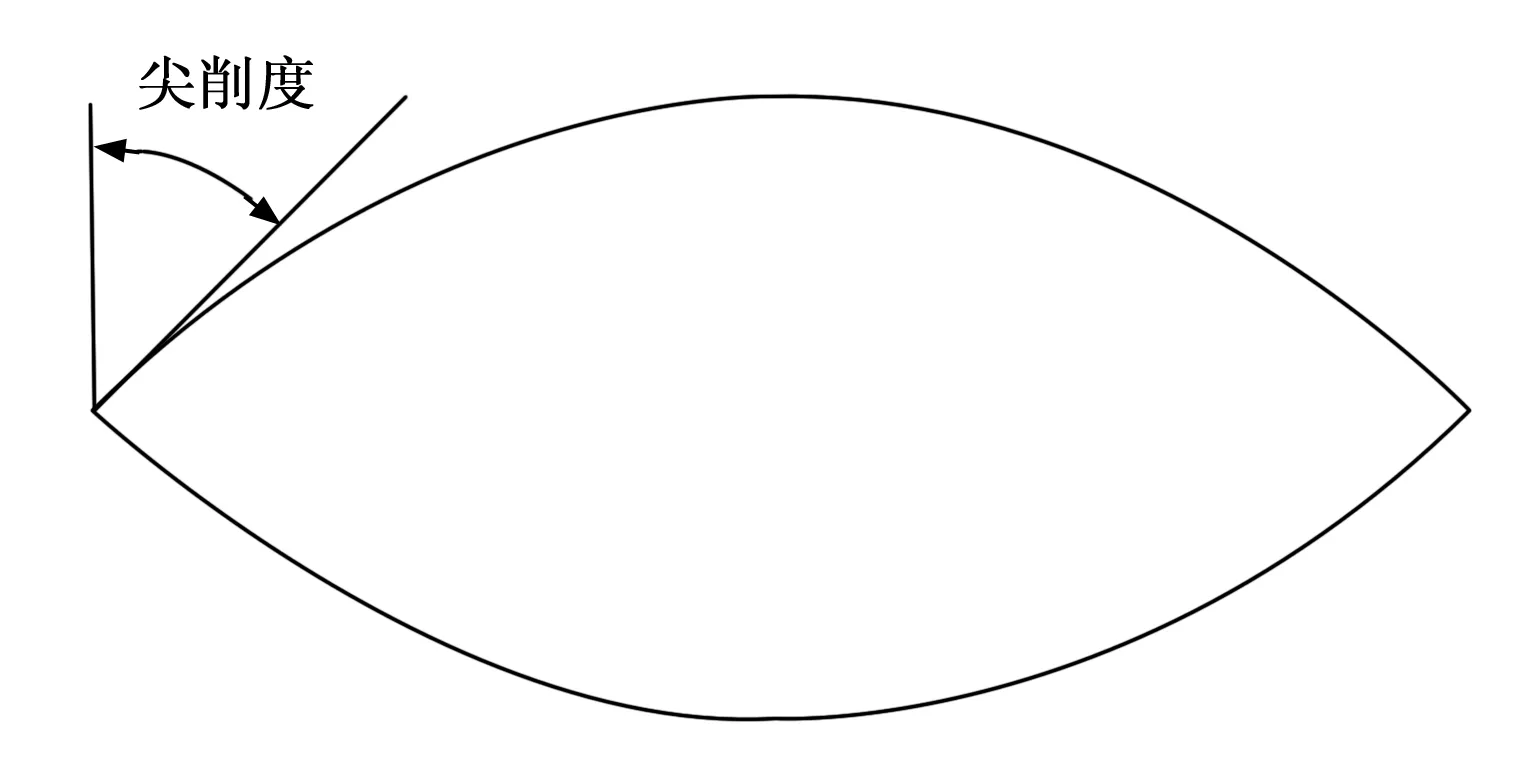
图6 尖削度定义

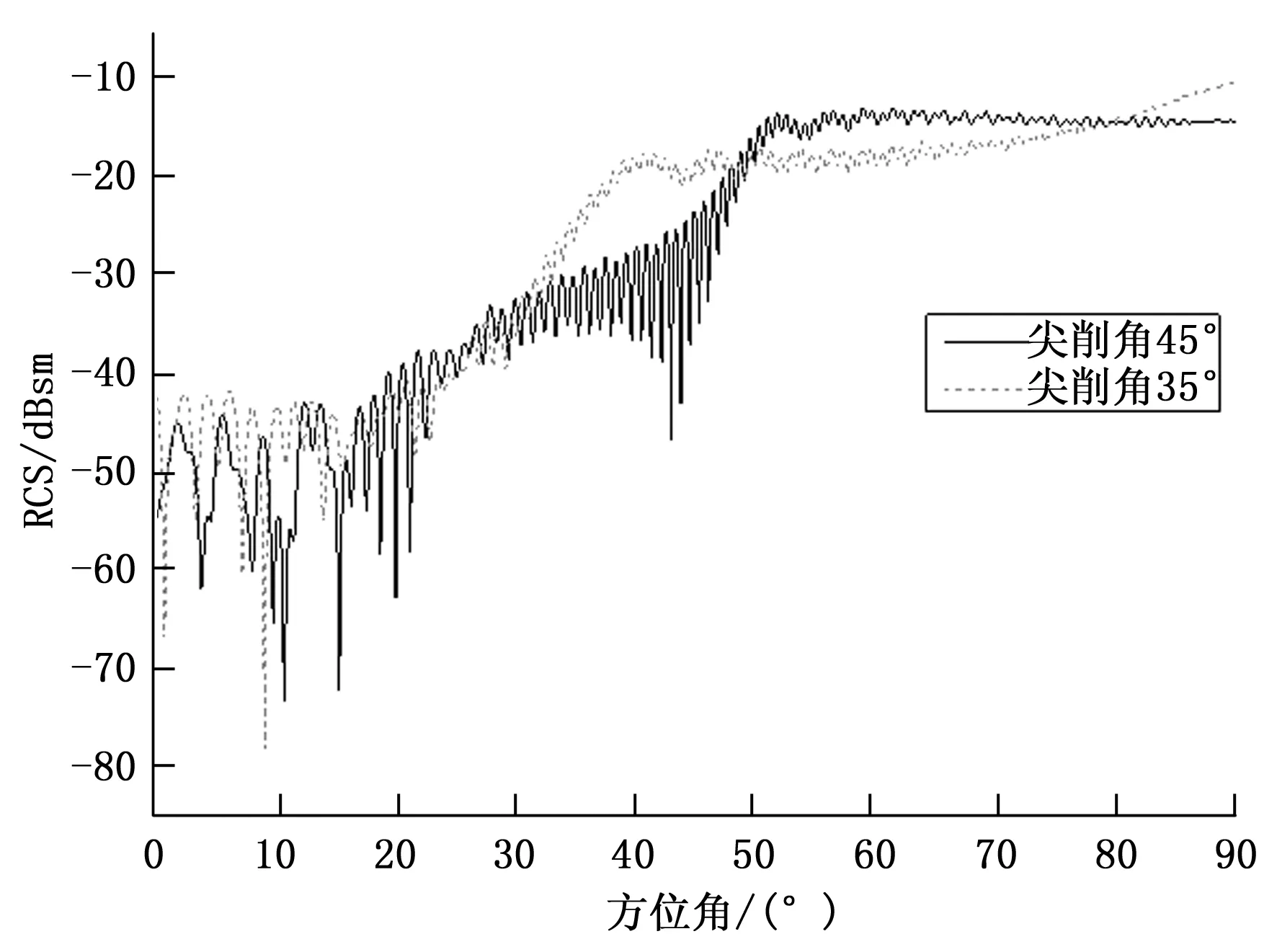
(a)尖削度45°和35°散射特性(水平极化)

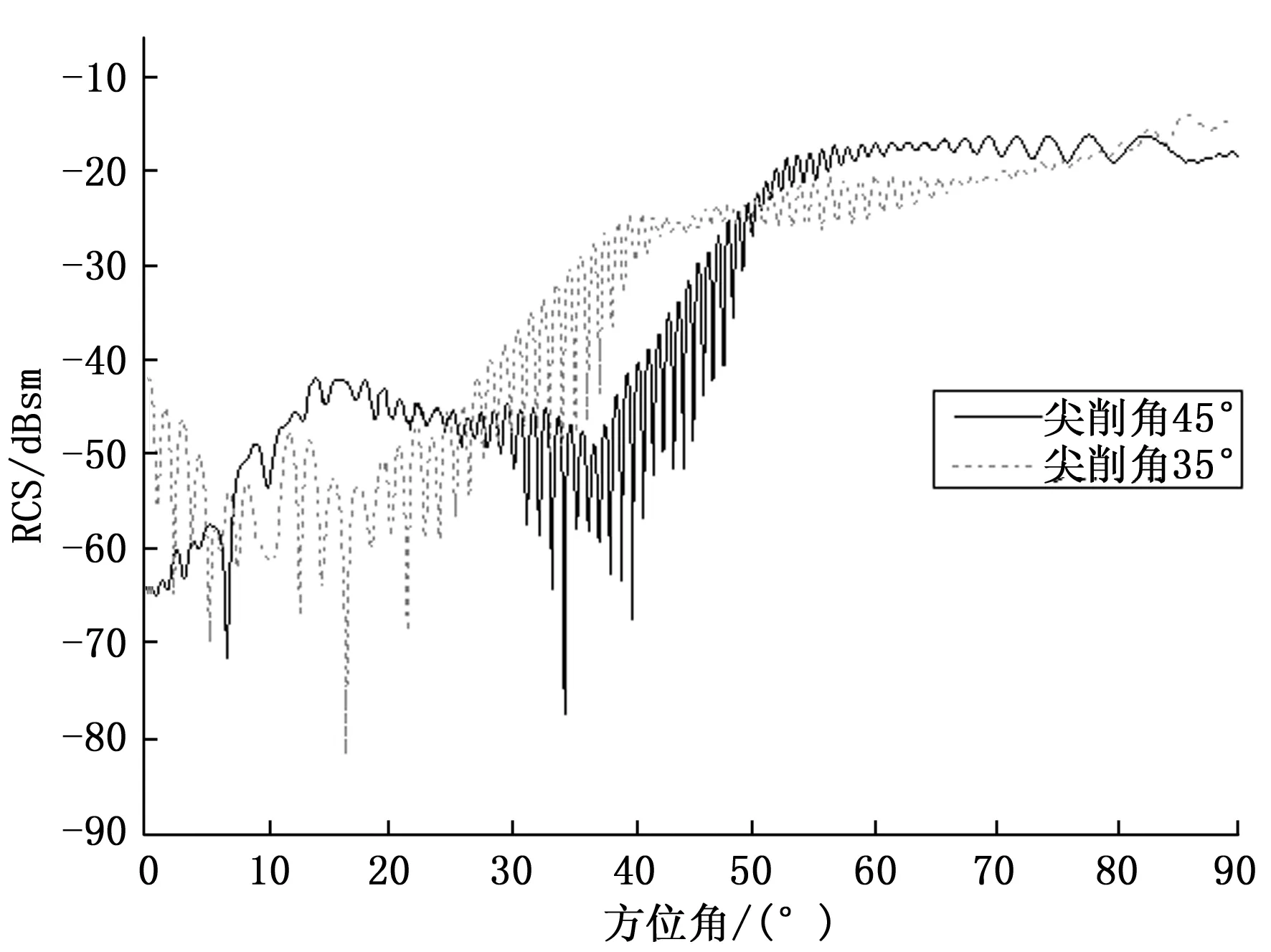
(b)尖削度45°和35°散射特性(垂直极化)图7 散射特性图

通过对图7中的数据进行分析，在水平极化下0～50°方位角范围内，尖削度为45°的载体散射水平在大部分方位角下普遍低于尖削度为35°的载体散射水平，其中，前者的RCS均值为0.0011 m2，后者的RCS均值为0.0034 m2。

垂直极化下0～50°方位角范围内，尖削度为45°的载体散射水平与尖削度为35°的载体散射水平各有高低：0～10°方位角范围内，尖削度为45°的载体散射水平低于尖削度为35°的载体散射水平，10～25°方位角范围内，尖削度为45°的载体散射水平高于尖削度为35°的载体散射水平，25～50°方位角范围内，尖削度为45°的载体散射水平又低于尖削度为35°的载体散射水平，导致垂直极化下不同方位角范围内不同尖削度载体散射水平各有高低的原因是由于不同散射源的相互耦合，从而导致在不同方位角下占主导地位的散射源在不断的变化。经过均值计算，垂直极化下0～50°方位角范围内，尖削度为45°的载体的RCS均值为0.0002 m2，尖削度为35°的载体的RCS均值为0.0008 m2。在50～90°范围内，由于外形隐身设计的特点，前向散射水平的降低带来了侧向散射水平的升高，导致两个极化下尖削度为45°的载体散射水平普遍高于尖削度为35°的载体散射水平。由于现代隐身飞行器主要强调的是突防时前向隐身能力，故载体的设计也应采取较大的尖削角度。同时加大尖削度对载体前向角域内RCS减缩对水平和垂直极化均适用。

3.4 倒圆半径对其RCS的影响

载体曲面和平面连接处由于制造工艺的限制，一般以倒圆进行过渡。倒圆半径应尽可能小，以降低其边缘绕射对载体散射水平的影响。为对比不同棱边半径对载体RCS的影响，仿真计算了尖锐棱边R0 mm与半径R10 mm的棱边载体的RCS方位角特性如图8所示。

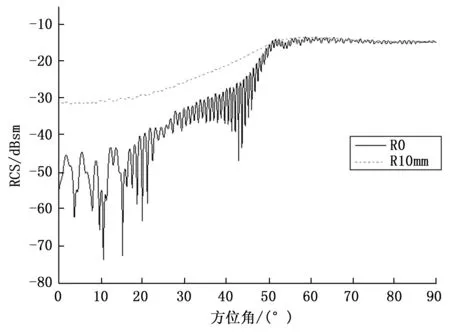
(a)尖锐棱边载体和棱边倒圆半径R 10 mm载体散射特性(水平极化)

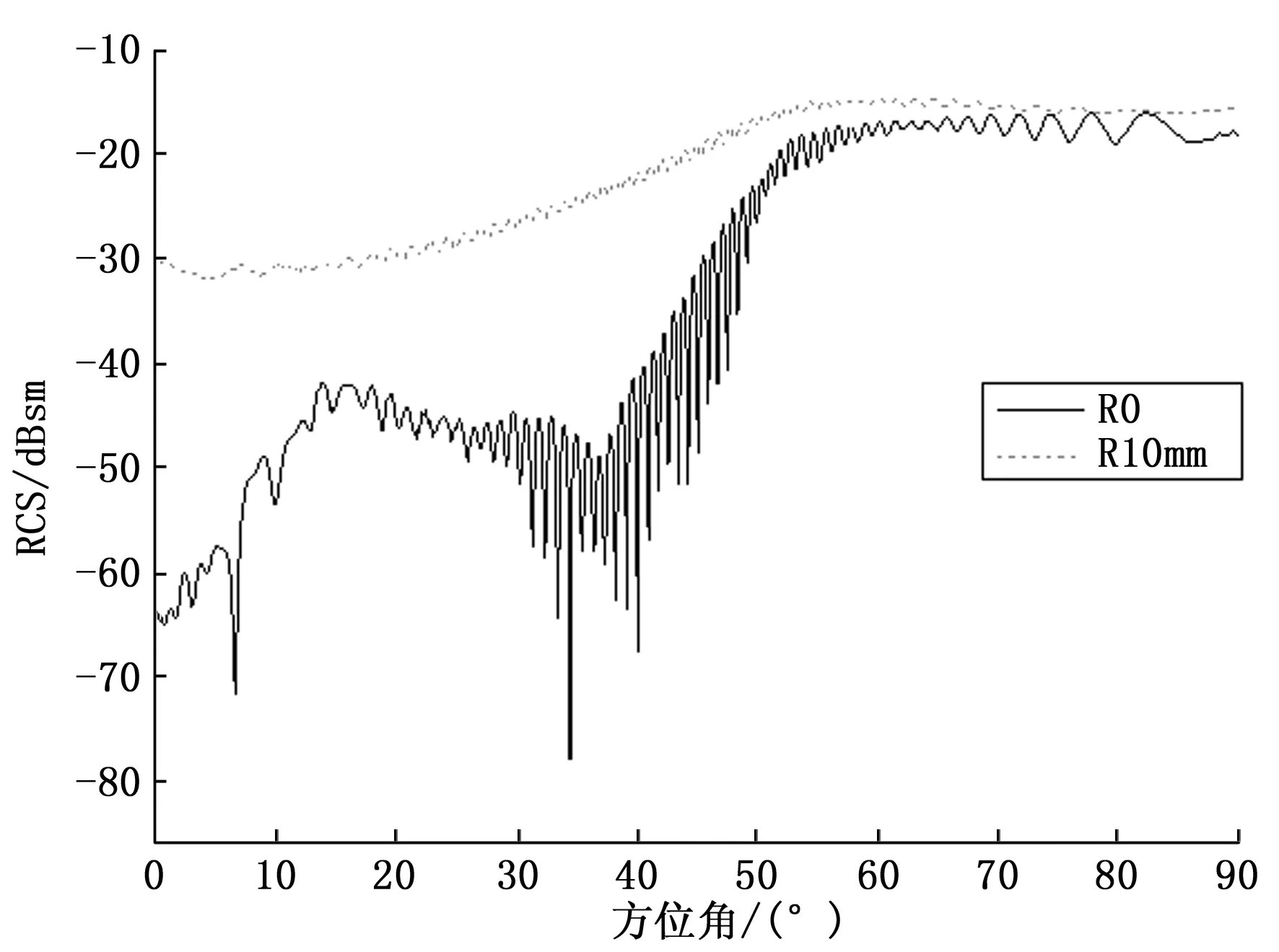
(b)尖锐棱边载体和棱边倒圆半径R 10 mm载体散射特性(垂直极化)图8 散射特性图

通过对图8中数据进行分析，两个极化下在0～50°方位角范围内，棱边半径R10 mm的载体其散射水平普遍大于尖锐棱边的载体，同时由于棱边的漫反射导致其RCS曲线没呈现出剧烈的振荡特性，RCS随方位角的变化不敏感，50～90°方位角范围内，入射波以较大的入射角入射时。两者的RCS曲线较为接近。经过均值计算，在0～30°方位角内水平极化下，棱边半径R0 mm的载体和棱边半径R10 mm的载体其RCS均值分别为0.000068304 m2和0.001178579 m2，垂直极化下分别为0.000024167 m2和0.001114341 m2，两个极化下棱边半径R10 mm的载体比棱边半径R0 mm的载体RCS均值大两个量级。考虑到制造工艺的因素，倒圆半径应尽可能小，以减小棱边的漫反射造成的RCS剧增。

4 结束语

基于多层快速多极子算法对不同连接方式、尖削度、倒圆半径的低散射载体进行了仿真分析。仿真计算结果表明，在X波段水平极化和垂直极化下，设计的低散射载体在0～30°方位角范围内RCS低于-30 dBsm，0～20°方位角范围内RCS低于-40 dBsm，掠入射时低于-30 dBsm，处于较低的散射水平，可用于台阶、缝隙类目标RCS测试。

设计低散射载体应注意遵循以下准则：

1)为减低前向散射水平，载体的横向对缝应设计成曲率连续；

2)台阶与缝隙应位于载体上的曲面一侧；

3)为减低前向散射水平，应尽可能加大前缘尖削度，将散射峰值偏移到前向关注的角域外；

4)减小连接曲面之间的倒圆半径，以降低其边缘绕射。

[1] 张 考，马东立.军用飞机生存力与隐身设计[M]. 北京：国防工业出版社，2002.

[2] 桑建华.飞行器隐身技术[M]. 北京: 航空工业出版社, 2013.

[3] 桑建华，周 海. 飞行器表面电磁缺陷及雷达吸波材料应用[J]. 航空材料学报，2003，23(2)：51-55.

[4] 黄沛霖，刘战合. 飞行器表面缝隙电磁散射特性研究[J]. 航空学报，2008，29(3)：675-680.

[5] 桑建华，张宗斌，王 烁. 低RCS飞行器表面弱散射源研究[J]. 航空工程进展，2012，3(3)：257-263.

[6] 张 扬，艾俊强，王 健，等. 倾斜双垂尾L频段电磁散射特点分析[J]. 电讯技术，2015，55(11)：1260-1265.

[7] 李永俊.电磁理论的高频方法[M]. 武汉：武汉大学出版社, 1999.

[8] 袁浩波，高屾林，李 兵，等.一种高精度求解磁场积分方程的高阶矩量法[J]. 西安交通大学学报，2013，47(12)：61-65.

[9] 张宗斌，陈益邻，高正红. 三维复杂目标求解的多层快速多极子方法[J].南京航空航天大学学报，2007，39(2)：222-226.

[10] 黄小忠，曹伟华，杜作娟，等.高频电大尺寸飞机目标的矩量法分析[J]. 计算机仿真，2012，29(5)：37-41.

[11] 满明远，雷振亚，谢拥军，等.电大目标散射问题的预修正多层快速多极子分析[J]. 西安电子科技大学学报(自然科学版)，2012，39(2)：133-137.

[12] 邹 昕. 电大尺寸复杂目标RCS快速求解的方法[J]. 西安工程大学学报，2013，27(2)：193-197.

[13] 董 健，庞 晨，温沙蒙，等.基于并行MLFMA算法的大规模电磁场并行数值仿真计算软件[J]. 计算机工程与科学，2013，35(3)：31-37.

Design and Simulation of Low Scattering Carrier in RCS measurement

Liang Shuang,Liu Qingjie,Nie Tun, Guo Wen, Zhang Bin

(AVIC Chengdu Aircraft Industrial (Group) Co.,Ltd.,Technical Center,Chengdu 610092,China)

The design results of low scattering carrier are determined by the scattering level of measured object. In order to implement detailed stealth design and obtain the scattering level of steps and gaps, the design methods of low scattering carrier used for RCS measurement of steps and gaps were proposed.Multilevel fast multipole algorithm (MLFMA) was appliedand the impacts of combination manner of adjacent surface, location, tapering ratio, and fillet radius on the scattering level were analyzed. The simulation results demonstrated that it could effectively reduce scattering level to reduce curvature fluctuation, increase tapering ratio, and reduce fillet radius. The steps and gaps should be located in the surface instead of the plane due to the fact that the scattering level of the surface was less than that of the plane. The method is of guidance meaning for the design of low scattering carrier in RCS measurement.

radar cross section (RCS); multilevel fast multipole algorithm (MLFMA);low scattering carrier;electromagnetic scattering;stealth design

2017-04-21；

2017-05-14。

梁 爽(1982-)，男，四川自贡人，工学硕士，工程师，主要从事飞机总体设计和隐身设计方向的研究。

1671-4598(2017)08-0104-04

10.16526/j.cnki.11-4762/tp.2017.08.027

V218

A