基于能量流动双PWM协调控制

丁博文，范 波,2，廖志明，郭 宁，张炜炜

(1.河南科技大学 信息工程学院，河南 洛阳 471023； 2.中信重工机械股份有限公司，河南 洛阳 471039；3.洛阳卡瑞起重设备有限公司，河南 洛阳 471023)

基于能量流动双PWM协调控制

丁博文1，范 波1,2，廖志明3，郭 宁1，张炜炜1

(1.河南科技大学 信息工程学院，河南 洛阳 471023； 2.中信重工机械股份有限公司，河南 洛阳 471039；3.洛阳卡瑞起重设备有限公司，河南 洛阳 471023)

基于双PWM结构，根据系统能量流动分析系统在能量平衡状态和能量不平衡状态下系统各部分间的能量关系，并建立双PWM结构能量数学模型；针对系统输出能量与消耗能量不平衡时造成的直流母线电压波动以及输出功率不匹配的问题，建立关于直流母线电压以及网侧电流d轴分量的约束条件，保证系统能量能够平滑变化；采用约束条件对整流器电压外环以及功率内环进行修正，用以实现整流侧输出能量与逆变侧消耗能量的快速平衡，达到双PWM结构间协调控制的目的；根据仿真结果表明，系统在电机功率突变时，能够实现能量的快速平衡，并且能够减少直流母线电压波动，减少网侧谐波分量和直流侧电容。

能量流动；约束条件；能量平衡；协调控制

0 引言

随机新能源技术和交流变频技术的发展，双PWM变换结构在整流侧与逆变侧的电路相似，采用适合的控制策略能够实现系统高功率因数输出，以及直流电压可调，抑制网侧谐波等，所以越来越被国内外专家学者关注，尤其在新能源领域和交直交变频技术领域有广泛应用[1]。

双PWM变换结构可分为整流侧和逆变侧，对于整流侧控制方法许多种。大致可分为：直接功率控制(Direct Power Control，DPC)，直接电流控制(Direct Current Control，DCC)和模型预测控制(model predictive control，MPC)等[2]。直接功率控制采用的是PWM整流器d-q坐标系下功率数学模型，并且由于该控制方法具有结构简单，响应速度快，固定开关频率等优点被广泛应用于整流侧,文献[2]采用直接功率控制，在功率内环采用PI控制器控制，控制无功功率为0。而直接电流控制与直接功率控制不同之处在于系统内环为电流内环直接控制系统的有功电流于无功电流。直接电流控制也具有响应速度快的优点，但结构相对复杂，在应对负载功率突变时有一定的局限性[4]。文献[5]采用模型预测控制与直接功率控制和直接电流控制不同之处在于系统内环采用模型预测算法替代了PI控制器，虽然模型预测算法简化了系统的结构，降低了系统的设计难度，但是往往存在一定的静差难以消除，并且对系统各部分参数较为敏感。为了体现系统的各部分之间的能量关系并且综合各个控制方法的优缺点，所以本文整流侧采用直接功率控制。

而对于双PWM控制方法也有许多种，如：独立控制策略，主从控制策略等。独立控制策略就是将整流器与逆变器视为对立结构独立控制。这种控制方法较为简单，设计难度较小但是鲁棒性不强。而主从控制策略，就是将逆变器作为主要控制部分而把整流器视为从属部分，根据逆变器输出信息来控制整流器。负载功率前馈就是一种典型的主从控制策略，文献[6]使用负载功率前馈，将负载功率前馈至整流侧，实现整流器输出功率的提前调节。而文献[8]采用控制电容电流的方法实现电容在负载功率突变时刻消耗的功率接近于0，达到抑制直流母线电压波动的目的，但是本质上仍旧是主从控制。

虽然对双PWM结构的控制方法有许多种，但是其本质都是基于电流数学模型或者是基于功率数学模型，并没有从能量的角度分析双PWM变换结构。双PWM变换结构的优点之一就是能够实现能量的双向流动，从能量角度更能够说明引起系统输出输入功率不平衡的原因，从而加以控制。文献[9]虽然给出来了系统各部分之间的功率关系，但是并没有说明系统各部分能量间的关系。

因此本文整流侧采用直接功率控制，而对于整个双PWM变换结构，推倒其各部分之间的能量关系，建立系统能量数学模型。根据数学模型设定约束条件对整流器功率内环，和电压外环进行矫正，保证整流侧与逆变侧的协调控制。最后通过搭建仿真模型进行试验来对其有效性进行验证。

1 d-q旋转坐标系下双PWM结构功率数学模型分析

1.1 d-q坐标系下PWM整流器功率数学模型分析

PWM整流器拓扑结构如图1所示。

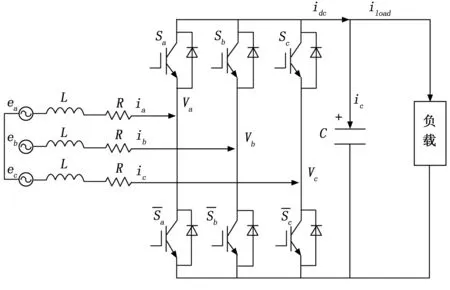
图1 三相电压型PWM整流器主电路

图1中，ea、eb、ec为网侧电动势，Lg为网侧滤波电感，R为网侧电阻，Cdc为直流侧电容，Sx为功率开关器件开关信号，Va、Vb、Vc为PWM整流器输入电压。

设网侧电动势为es，则在两相α-β静止坐标系下，可得eα=escosωt、eβ=essinωt。若α-β静止坐标系以同步角频率ω旋转，则成为d-q旋转坐标系，令电源电动势与d轴重合并结合瞬时功率理论可得d-q旋转坐标系下瞬时功率表达式为：

p=edid

(1)

q=-ediq

(2)

由文献[10]结合式(1)、(2)可得d-q旋转坐标系下PWM整流器功率数学模型。

(3)

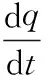
(4)

(5)

式中,p，q为PWM整流器输出的有功功率与无功功率，ω为电源旋转角频率，ed，eq为电源电动势d-q轴上的分量，vd，vq为PWM整流器在d-q轴上的输入电压分量，pdc为直流侧功率，pload为负载功率。

1.2 m-t坐标轴下三相异步电动机数学模型

对电机控制的方法有许多种，比如：直接转矩控制、转子磁链定向控制等。本文采用了按照转子磁链定向的控制方法，转子磁链定向控制方法是将逆变器与三相异步电机视为一体，采用矢量控制，将转子磁链与d-q旋转坐标d轴重成为新的旋转坐标系，可称为m-t轴坐标系，该坐标系旋转速度为定子磁链的同步角频率ω1。由文献[12]可得m-t坐标系下的三相异步电动机数学模型。

m-t坐标系下三相异步电机电压方程：

(6)

m-t坐标系下三相异步电机磁链方程为：

(7)

m-t坐标系下三相异步电机转矩方程为：

Te=npLm(istirm-ismirt)

(8)

m-t坐标系下三相异步电机运动方程：

(9)

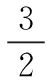
根据三相异步电机数学模型设计三相异步电机按照转子磁链定向控制结构，如图2所示。

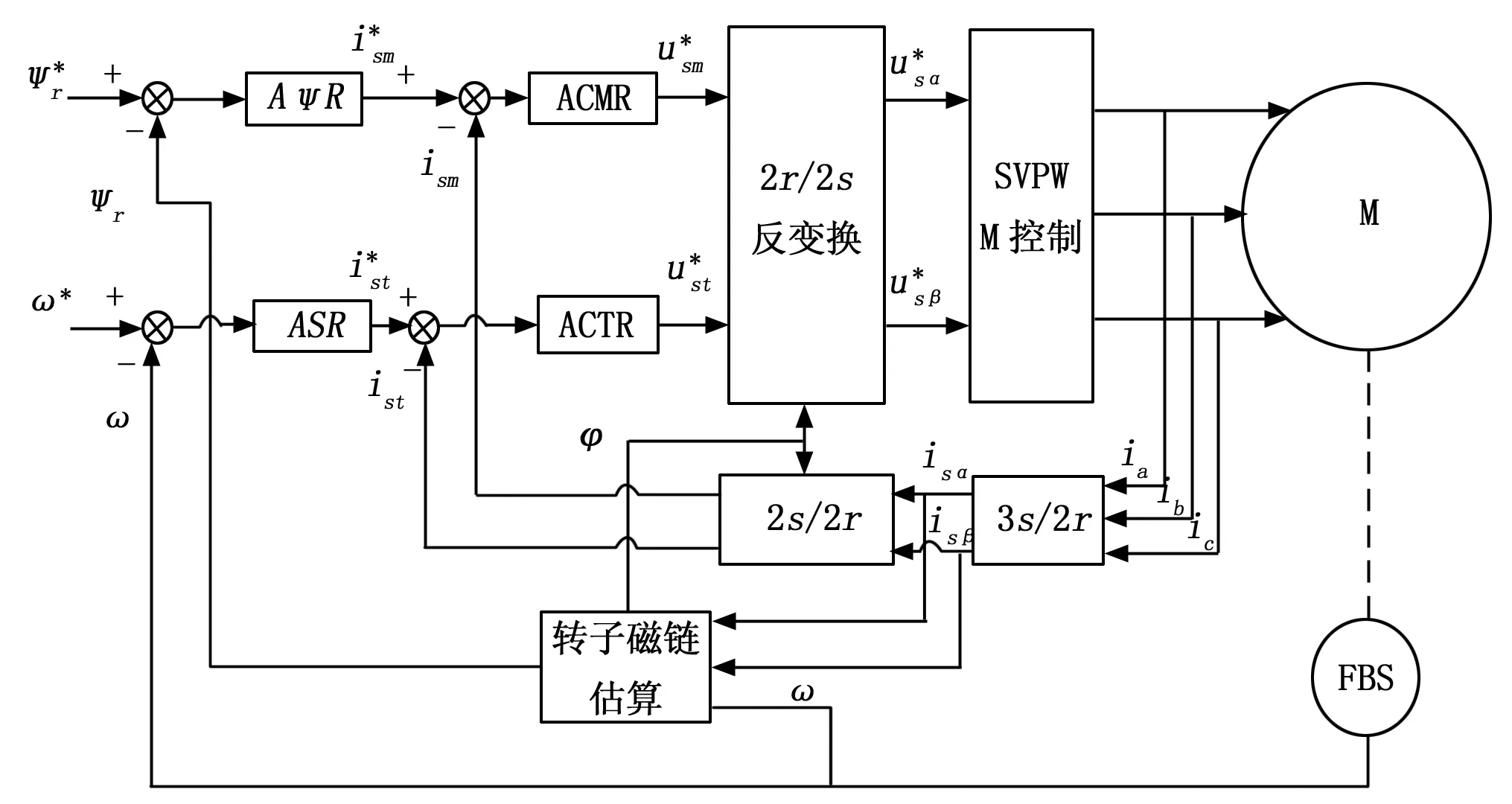
图2 三相异步电机转子磁链定向控制结构图

图中，AψR为转子磁链控制器，ASR为转速控制器，ACMR为磁场电流控制器，ACTR为转矩电流控制器，FBS为转速传感器。根据控制结构图可知，通过控制励磁电流ism和转矩电流ist就能够实现对电机转速和转子磁链的控制。根据前文所述的PWM整流器功率数学模型，负载功率Pload=udciload。本文采用转子磁链定向的方法控制电机，负载电流iload在m-t旋转坐标系下被分解为励磁电流ism和转矩电流ist。所以可以假设负载电流iload在空间上也是以同步角频率旋转，如图3所示。

图3 m-t坐标系下负载电流

故针对系统采用转子磁链定向方法时，负载电流可表示为：

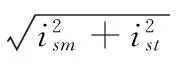
(10)

2 双PWM控制结构能量数学模型分析

2.1 双PWM控制结构能量数学模型

双PWM控制结构中的能量可分为4个部分，分别为：网侧滤波电感中储存的能量、网侧电阻的耗能、直流侧电容存储的能量以及负载侧电机的耗能。故根据能量平衡原理可得：

P=PL+PR+PC+PM

(11)

P为网侧输出的总功率，PR为网侧电阻功率，PL为网侧滤波电感功率，PC为直流侧电容功率，PM为负载电机消耗的功率。PWM整流器采用直接功率控制，使系统的无功功率为0。在d-q旋转坐标系下，无功电流iq为0。所以电网输出电流在d-q旋转坐标系下为id。网侧滤波电感功率为：

(12)

将式(12)一阶倒数离散化为：

(13)

式(13)中，Ts为系统采样周期。故可用式(13)表示一个采样周期能量变化。对于n个采样周期电感能量可表示为：

(14)

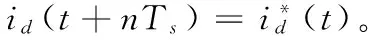
(15)

直流侧电容功率为：

(16)

同理将式(16)一阶倒数离散化并求n个系统采样周期电容能量为：

(17)

网侧电阻功率为：

(18)

对式(18)积分，积分上限为t+nTs，求得n个系统采样周期，网侧电阻的耗量。

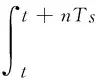
(19)

负载三相异步电机功率为：

Pload=udciload

(20)

同理可得n个系统采样周期，异步电机耗能为：

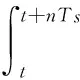
(21)

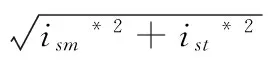
电网输出功率为P，那么同理可得n个系统采样周期电网输出的能量为：

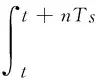
(22)

那么根据上文分析，可得系统从t时刻至t+nTs的能量变化为：

ΔE=E(t+nTs)-E(t)=EL+ER+EC+Eload

(23)

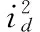
(24)

即网侧输出的能量全部被网侧电阻和负载电机吸收，符合能量平衡原理。

2.2 双PWM控制结构能量失衡控制原理分析

根据式(24)可知系统处于稳态时，系统能量的输入与输出之间的关系。这种关系能够适用于系统大部分时间。但对于交-直-交变频调速控制系统而言，交流电机经常会出现刹车制动，转速突变，转矩突变等情况，而在这钟情况下，系统就不再是稳态，系统需要一定的时间进行调节恢复至稳态。所以分析系统从变化时刻至恢复至稳定时刻的各部分之间的能量关系是很有必要的。

假设t时刻由于负载电机功率突变导致系统处于能量不平衡状态，系统经过nTs的时间恢复至稳态。根据前文所述得到系统不平衡状态的数学关系式为：

(id*-id)edTs=Lg(id*2-id2) +Cdc(udc*2-udc2) +

RTs(id*2+id2) +Ts(udc*iload*+udciload)

(25)

整理式(25)可得：

(2)合同主义的立法，即需征得生母的同意之立法。在英国，依据1989年《儿童法》，任意认领的生效要件是:夫妻双方达成协议;协议必须“采用规定的形式”(in the prescribed form);向法院登记。“法院的功能是行政性的，而非司法性的;法院在登记时并不调查儿童的福利。”㉑在德国，“承认自己为父的男子，须按照规定的形式作出单方的、无需受领的意思表示。承认父的身份必须获得母的同意(《德国民法典》第1595条第1款)。”㉒另一方面，根据“承认”而“被认定为父的男子，有可能并非子女的生父。为了矫正这种偏差，法律允许通过法院裁判撤销父的身份”㉓。

Cdcudc2-Tsudciload-Cdcudc*2-Tsudc*iload*=

(RTs-Lg)id2+idedTs-id*edTs+Lgid*2+RTsid*2

(26)

f(udc) =Cdcudc2-Tsudciload-Cdcudc*2-Tsudc*iload*

(27)

Cdc为正值，且存在实根。故该函数存在极小值，即当直流母线电压满足：

(28)

在这个约束条件下，逆变侧能量变化率最小，同样整流侧的能量变化率也是最小。

将该约束条件式(28)代入式(26)可得：

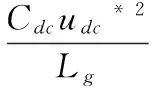
(29)

(30)

(31)

(32)

根据式(28)、(32)可知，系统直流母线电压与网侧电流d轴分量与负载电流有直接关系。并且可根据该约束条件对整流器电压外环和功率内环进行修正。实现系统能量平滑调节的目的。

3 仿真分析

在上述理论研究的基础上，在Simulink仿真平台上搭建双PWM仿真模型。仿真参数：整流器相电压有效值220 V，网侧电感Lg=15 mH，直流侧电容Cdc=8 000 uF，直流母线电压指令值udc*=700 V，采样频率f=5 000 Hz。逆变器输出频率50 Hz。三相异步电动机容量5 000 VA，，采样频率帆f1=5 000 Hz，转子电感Lr=0.002 H，转子电阻Rr=0.816 Ω，定子电感Ls=0.002 H，定子电阻Rs=0.435 Ω，电动机转速指令值800 rad/s，磁链指令值1。

由于双PWM控制结构可以分为整流侧和逆变侧两部分，为了验证仿真的准确性，所以首先用电阻替代逆变侧的电机和逆变器验证在约束条件下，对PWM整流器功率内环和电压外环的修正的有效性。然后将电阻替换成为逆变器和电机构成双PWM结构经行仿真实验，验证系统整体性能。

对比分析PWM整流器采用直接功率控制时，采用约束条件的系统与不采用约束条件的系统在负载功率变化时的性能。PWM整流器控制结构分为功率内环和电压外环。所以可以在功率内环有功功率控制环节进行修正以及在电压外环对电压经行修正。负载为400Ω电阻，在0.2 s时，负载突变为200 Ω。如图4所示。

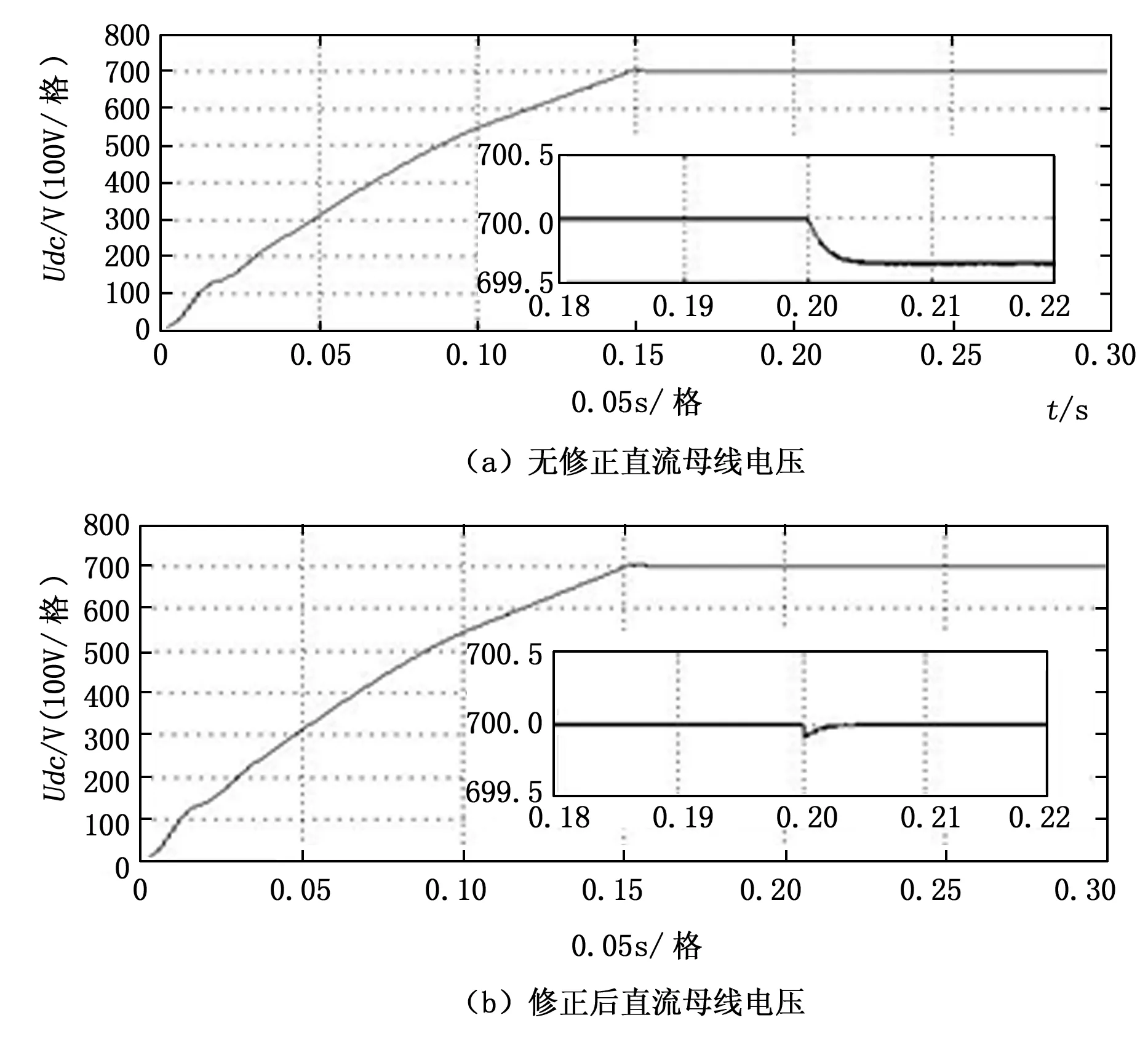
图4 负载功率突变直流母线电压波形图

图4(a)为电压外环采用PI控制器并且并未采用约束条件的控制系统，0.2 s时负载功率突变，直流母线电压压降约为0.3 V，但直流母线电压存在静差难以调节。图4(b)为采用约束条件对电压外环和功率内环进行修正，在0.2 s时负载功率突变，直流母线电压压降几乎可以忽略不计，并且不存在静差，系统能够快速回到稳态。

电网侧谐波分量以及功率因数同样是衡量系统性能的一个重要指标。以网侧a相为例，如图5所示。

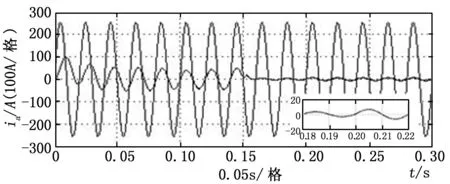
图5 网侧a相电流电压

图5中，当系统稳定，网侧电压、电流能够实现同相位。并且在负载功率突变时刻，电压并未出现明显畸变，能够平滑过度。这就说明系统能够实现高功率因数输出，并且谐波分量较小。功率因数如图6所示。

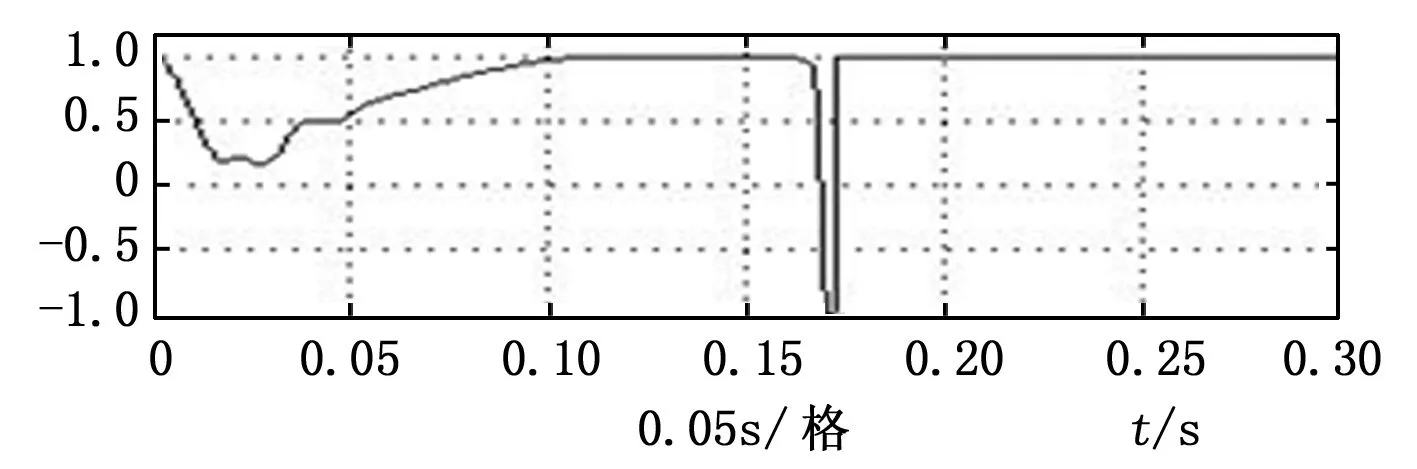
图6 系统功率因数

由图6所示，当系统稳定后，能够实现单位功率因数输出。

根据上述对PWM整流器电阻负载的仿真结果可以说明采用约束条件对系统进行修正是能够消除直流母线电压的静差，抑制直流母线电压的波动,同时能够减少网侧谐波分量。故本文对双PWM控制结构进行仿真分析。系统在0.4 s时，电机转矩突变为20 N·m。对比分析采用约束条件的控制系统与不采用约束条件的控制系统性能。双PWM直流母线电压波动如图7所示。

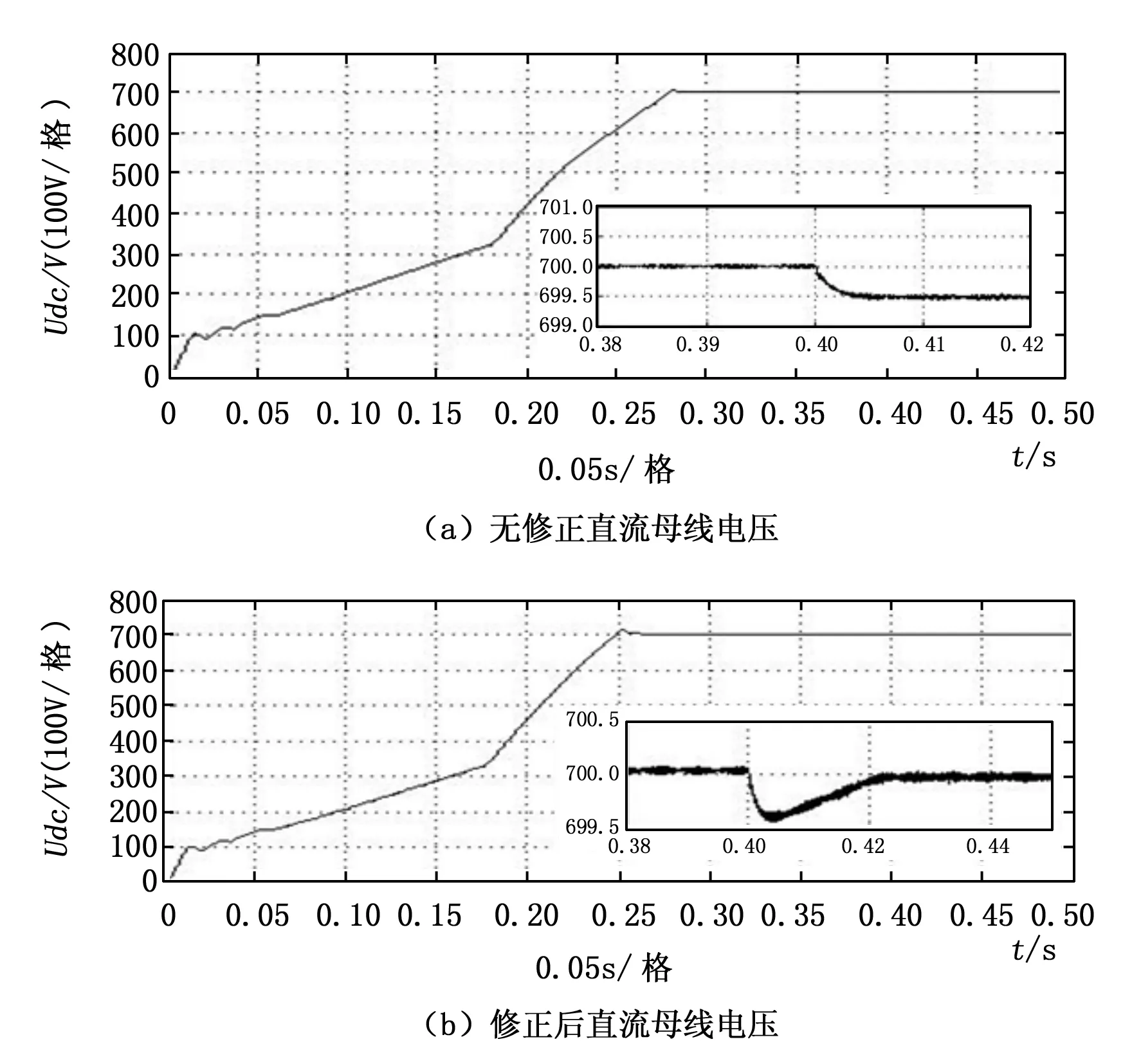
图7 电机转矩突变直流母线电压波形图

根据电压波动图可知，采用约束条件对系统进行修正是能够消除由于电机功率突变导致的静差，但相对于前文所述的纯电阻负载，系统调节时间有所增加。将突变后电机转矩升至40 N·m，同时减少系统直流侧电容为2 000 uF。直流母线电压如图8所示。

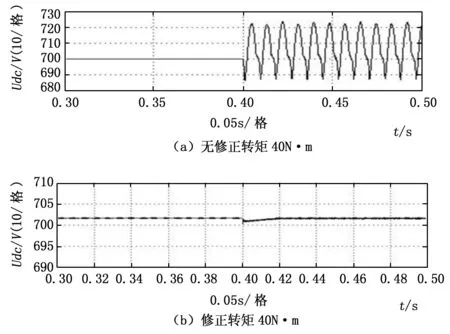
图8 电机转矩40 N·m直流母线电压波形图

由图8可知，电机转矩突变为40 N·m，同时减少直流侧电容。系统在无修正的情况下，直流母线电压大范围波动。采用约束条件对系统修正，当转矩突变为40 N·m，由于减少了直流侧电容，修正参数出现一定误差，造成约为2 V的静差，但是系统直流母线电压仍旧能够维持稳态。

无论采用哪种控制方法都能够保证三相异步电机电机的正常运行。但采用约束条件对系统进行修正时，由于三相异步电机类似于阻感负载，直接从直流母线上获得负载电流波动较大。故可根据式(10)得到负载电流。

电机转子磁链如图9所示。

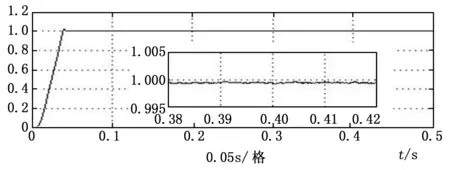
图9 电机转子磁链波形图

由图9可知电机转子磁链很快趋于稳态，并且电机转矩变化并未对电机磁链造成影响，三相异步电机可以部分等效为直流电机加以控制。但是由于三相异步电机励磁电流与转矩电流间存在一定的耦合性，所以磁链会存在一定的静差，但对系统影响不大。励磁电流与转矩电流如图10所示。

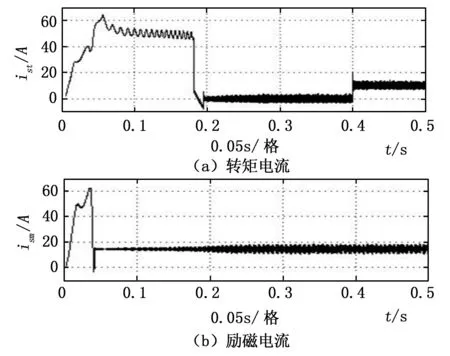
图10 励磁电流与转矩电流

由图10可知，系统励磁电流很快就趋于常量，建立电机内部磁场。但由于电流间的耦合性，0.2 s时，电机转速趋于指令值时，转矩电流突降，励磁电流也会随之受到影响，波形毛刺增多，转子磁链产生静差。

电机转速如图11所示。

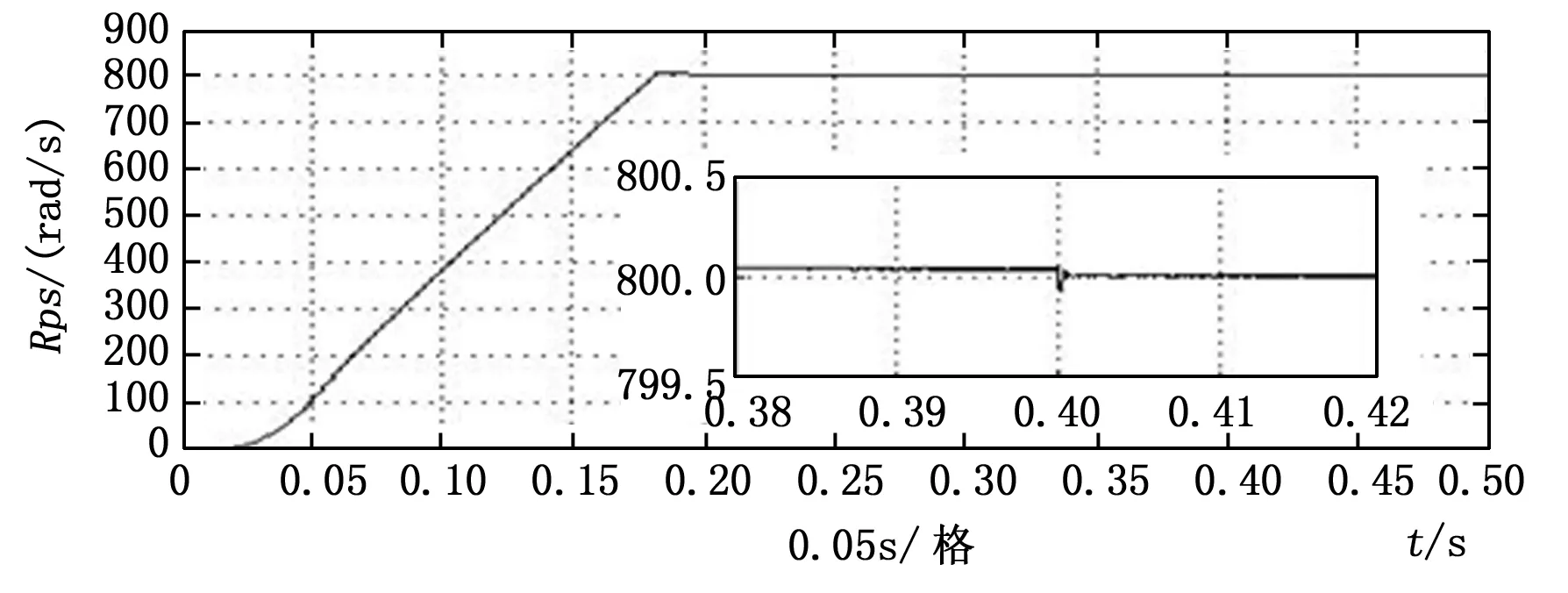
图11 电机转速

电机转速约在0.2 s时趋于指令值，系统存在约为0.1转的静差可忽略不计。在0.4 s时，电机转矩增大，电机转速降约为0.1转也可忽略不计。故在电机功率允许范围内，转矩突变对电机转速的影响不大。

4 结束语

本文详细分析了双PWM结构能量流动的特点，并从能量流动角度建立一段时间内系统能量变化的数学模型。在该数学模型的基础上建立约束条件使电机功率突变前后能量能够以平滑的方式进行调整，从而达到抑制直流母线电压波动，减少谐波分量的目的。根据仿真结果表明，采用约束条件对整流侧功率内环以及电压外环进行修正是能够抑制电压波动，减少网侧电流谐波分量，同时能够减少直流侧电容容量，保证电机的正常运行，实现双PWM协调控制。

[1] 郑 征, 徐 奔. 双PWM变频器电容电流反馈控制的研究[J].电气传动自动化，2011,33(6):1-5.

[2] 苏晓东, 焦 姣. 基于瞬时功率理论的电压型PWM 整流器研究[J]. 电力电子技术, 2010, 44(10): 54-56.

[3] 刘秀翀, 张化光, 褚恩辉, 等. 三相电压型PWM整流器功率控制方法[J]. 电机与控制学报, 2009, 13(1): 48-49.

[4] 石健将, 李荣贵, 张 平, 等. 基于新型电压电流双闭环控制的轴带发电机PWM整流器研究[J].电工技术学报，2014. 29(6): 189-194.

[5] 罗德荣, 姬小豪, 黄 晟, 等. 电压型PWM整流器模型预测直接功率控制[J].电网技术，2014, 38(11): 3111-3114.

[6] 李昆鹏, 万健如, 宫 成, 等. 双PWM变换器一体化控制策略[J]. 电机与控制学报, 2013, 17(4) : 72-78.

[7] 王秋梅, 尹 赟, 宋文祥. 双PWM 变换器功率前馈控制方法[J]．电气传动自动化，2013，4(35): 15-18.

[8] 戴 鹏, 朱方田, 朱荣伍, 等. 电容电流直接控制的双PWM 协调控制策略[J].电工技术学报，2011,26(1):176-141.

[9] 肖 雄, 张勇军, 王 京, 等. 基于全响应功率补偿的电压型 PWM整流器直接功率控制[J].电工技术学报，2015, 4(30): 113-119.

[10] 黄 静, 杨柏旺, 吴志清, 等. 基于负载功率前馈的PWM整流器控制策略[J]. 电力电子技术, 2014, 48(11): 61-64.

[11] 张 兴, 张崇巍. PWM整流器极其控制[M]. 北京：机械工业出版社.

[12] 阮 毅, 陈伯时. 电力拖动自动控制系统[M].北京：机械工业出版社.

[13] 张 帆, 刘跃敏, 范 波, 等. 三相电压型PWM整流器模型预测直接功率控制[J].计算机测量与控制， 2016, 24(9): 122-129.

Double PWM Coordinated Control Based on Energy Mathematic Model

Ding Bowen2, Fan Bo1,2, Liao Zhiming3, Guo Ning2, Zhang Weiwei2

(1.College of Electrical Engineering, Henan University of Science and Technology,Luoyang 471023, China;2.CITIC Heavy Industries Co., Ltd. Luoyang 471039, China; 3.KRC Crane Equipment Co.,Ltd.Luoyang 471023, China)

Based on double PWM structure, analyses each part of system energy relationship on the basis of system energy flow theory when system in the energy balance state and unbalance state and build energy mathematic model of double PWM. In order to solve the problem that the DC bus voltage fluctuation and the system output power not matches the system input power dues to the system output energy not matches the system input energy, build constraint condition of DC bus voltage fluctuation and grid-side current component in the d axis. The condition can ensure the system energy smoothly varies. Using constraint condition to correct voltage outer loop and power inter loop, realize the output energy of rectifier side can fast match with the loss energy of inverter side. So the double PWM structure can ensure each part coordinated control of system. According to results of simulation, the system can realize system energy fast in balanced state and reduce DC bus voltage fluctuation when the power of load motor suddenly varies. This method also can reduce the harmonic current and capacity of the DC side capacitors.

energy flow; constraint condition; energy balance; coordination control

2017-02-14；

2017-03-10。

国家自然科学基金资助项目(U1404512，61473115)；河南省重点攻关项目(162102210200)。

丁博文(1991-)，男，河南洛阳人，硕士研究生，主要从事电力电子与电气传动方向的研究。范 波(1975-)，男，河南洛阳人，副教授，硕士研究生导师，主要从事大容量功率变换与高压交流调速系统方向的研究。

1671-4598(2017)08-0058-06

10.16526/j.cnki.11-4762/tp.2017.08.016

TP319

A