基于最大长度序列的绝对位移精密检测方法

李 强，杨德华，费 飞，王敬东，王海涛

(南京航空航天大学 自动化学院，南京 210016)

基于最大长度序列的绝对位移精密检测方法

李 强，杨德华，费 飞，王敬东，王海涛

(南京航空航天大学 自动化学院，南京 210016)

为了检测精密机构的微小位移，根据位移编码与机器视觉技术，提出一种基于最大长度序列(Maximum Length Sequence—MLS)的绝对位移检测方法;该方法设计了基于MLS的绝对位移检测的视觉靶标方案，采用基于灰度叠加及二值化方法进行图像处理和靶标绝对位置识别；研究了基于拟合相位的精密定位方法，实现一维绝对位移的精密检测，并进行实验验证;实验结果表明，该方法可有效实现一维绝对位移检测，定位精度在±2 μm范围内，具有良好的重复性和鲁棒性，且无须视觉标定。

最大长度序列；绝对位移检测；视觉检测；灰度；拟合；相位

0 引言

在精密机构运行中，机构的微小位移是试验关注的重要数据之一，及时掌握此参数具有重要的实际意义[1]。对精密机构位移的测量，最常用的方法是采用位移传感器和基于激光测量的方法，位移传感器基于接触式测量，在特定场合下应用受到限制，基于激光测量的方法仪器昂贵，经济性在实际应用中受到限制[2]。将机器视觉用于精密机构检测，是当前发展的热点。国外Benjamin V Orozco和Victor G Garduno利用结构光技术对半径约为11 mm的球体和旋转约为130°的刚体分别进行测量[3]；Brent Carlson利用单CCD相机对望远镜光学镜精密机构进行多自由测量，其在2～12m的范围上测量精度可以达到200 μm[4]；国内张淑平等人利用双目法对六自由度大载荷实验平台进行了测量，其大线位移测量误差约3 mm[5]；陈若珠等人基于机器视觉技术的振动台试验变形位移测量误差在1.5 mm左右[6]；天津大学的张子淼等采用一种新的算法通过单相机和5个预设参考点计算出监测结构的位移，位移测量精度可以达到0.1 mm[7]。就目前所知的文献来看，基于单目、双目和结构光的非接触位移检测方法的精度尚有待提高。

将伪随机序列应用于位置测量领域也是近年研究的热点问题。日本电子通信大学Hirata等人研究了基于伪随机码的高灵敏度距离和位置检测专利[8]。上海交大唐恒博提出了基于m序列的轨道机器人高鲁棒定位方法[9]，北京交通大学王阳等人提出了基于伪随机数的光电轴角编码器，用于检测绝对角位移[10]。借鉴编码和译码的思想，并基于视觉技术，提出一种基于最大长度序列(Maximum Length Sequence - MLS)编码的位置靶标的非接触测量方法，应用于绝对位移的测量。

1 最大长度序列及其视觉靶标设计

常用的绝对式位移检测元件一般采用格雷码以避免自然二进制码存在的相邻位移示值突变造成的粗大测量误差的现象。采用传统二进制码设计的靶标编码也存在明显缺点，线位移编码器通常采用的纵向排列格雷码编码，标识每个位移的靶标必须由独立的一列n位序列组成，且每列序列无法为相邻位移的编码重复使用。

MLS序列由二进制伪随机数产生,对应于n位二进制伪随机数的最大长度序列总长为MLS=2n-1位。其最大的特点可为本测量方法利用的是：在其中任何位置的连续n位均是不重复的二进制数，即其中的任何一个n位二进制数的首尾n-1位均由其相邻的n位二进制数所共享而重复使用。据此，采用确定尺寸的靶标和确定尺寸的间距，利用MLS来设计绝对位移检测靶标编码。图1所示为n=6的最大长度序列，共63位；图中，以白条码代表“1”和以黑条码代表“0”时的对应的靶标图案。显然，基于MLS设计的一维绝对位移视觉靶标编码同图所示横向排列的二进制码类似，但是均匀连续排列，并且任一位置的n个靶标序列首尾n-1个靶标被相邻位移的n位靶标序列所重复使用。

图1 最大长度序列条码靶标

例如，最左边的6位子序列是“100000”，移动1位对应的子序列为“000001”，并且该序列任意所有的连续6位子序列都是唯一的，读取一个6位子序列(由CCD相机视觉成像后经过图像处理获得)，对应与靶标唯一确定的位置。首先将靶标定位在被测对象上，通过识别靶标图像位移就可以实现对被测对象的绝对位移检测，被测对象的位移，即靶标的位移。显然，这种靶标的检测精度只能达到每个条码的宽度，后文采用拟合相位的方法进行精密位移检测。

最大长度序列靶标也可以采用其他形式,本文采用了如图2所示的靶标设计。在黑色背景上设置两种不同长度的白色条带为有效靶标编码，即通过白条编码的长度不同区分“1”和“0”，较长的白条长度名义上设计为较短的两倍。白条编码名义宽度设计为w=1 mm，每两白条编码之间间隔等宽，也为w=1 mm，即白条编码图像本身黑白颜色名义变换周期为2w=2 mm。此靶标可看作每两位编码中间插入了全黑条码作为周期，因此也被称作插入周期条码的六位最大长度序列靶标。此条码经过适当的识别算法，可以得到更加精密的位移信息。

图2 插入周期的最大长度序列靶标

2 靶标图像处理和位置识别

对CCD相机拍摄的靶标图案的图像处理主要涉及两方面，一是图像的二值化，采用Otsu二值化算法进行处理。由于可能存在照明不均匀的效果，因此应该对图像中靶标进行区域分割并逐一进行二值化处理。二是可能存在畸变的图像中靶标图案的分割及其中心位置修正。可采用逐步搜索的方法搜索各靶标并进行分割，但将十分耗时。因此选取CCD相机视场中心像质最好的区域覆盖被测目标靶标矩阵，从而获得最好的靶标阵列图像。

当对一幅处理后靶标图像采样时，设每行每列的像素个数为M和N，则图像的像素总数为M×N,就构成了一个M×N的实数矩阵式(1)：

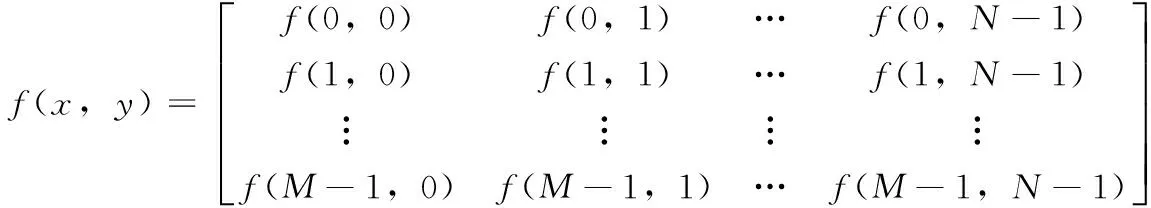
(1)

式中，二维点阵列中的每一个点的灰度值f(j,i)由采样得到，然后在经过二值化得到的灰度值(0或1),将每列像素点的灰度值求和，得到每列像素灰度叠加值g(i):

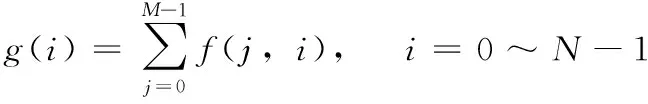
(2)

由g(i)即可分辨出相机采集的图像黑白条码，并可识别出其对应的二进制子序列，从而了解其在靶标MLS序列中的位置，即对应被测对象的绝对位置。

3 精密定位方法——相位拟合

采用图2的6位MLS靶标设计，CCD相机采集的其图像如图3所示。显然，不采用适当方法进行在分析处理，这种靶标的检测精度只能达到黑白颜色变换周期(下文简称编码周期)的一半，即为w=±1 mm。将图3每一列的所有像素的灰度值相加,可得到靶标图像的每列的灰度叠加值g(i)，如图4所示的短横线。可以直观地识别出从左边起第一个二进制子序列为100000。显然，该曲线是以靶标编码周期为周期的方波，其周期和相位信息采用一阶傅里叶变换，即正弦/余弦拟合可以获得，正是相位拟合信息反映本方法的位移定位信息。

G(x)=Asin(x+φ)+B

(3)

式中，G为灰度，φ为相位，A为幅值，B为直流分量，即背景。对灰度叠加值采用正弦拟合：可得到如图4所示的正弦曲线，而该曲线的相位可提供更精密的位移信息。

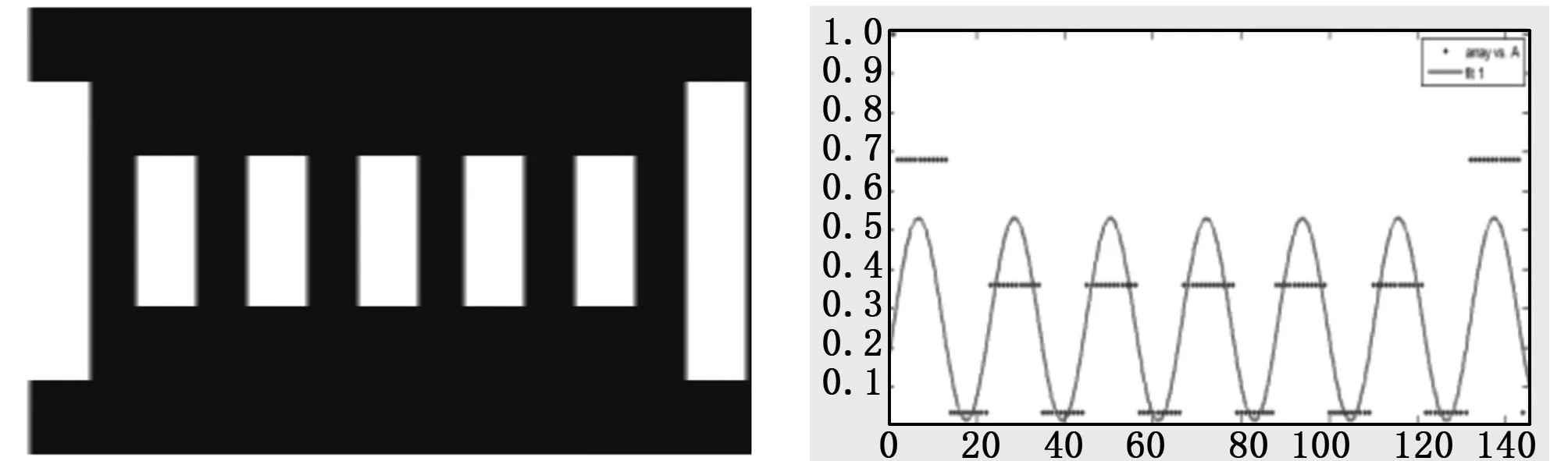
图3 靶标截图 图4 正弦拟合曲线

如图5和图6所示CCD相机采集的两幅靶标图像信息，前n(n=6)位对应的靶标子序列分别为111110和010101，根据最大长度序列编码特性，定位在被测对象上的靶标发生了a(此时a=5)个编码周期的位移。

图5 靶标编码111110 图6 靶标编码010101

经正弦拟合处理得：

G1(x)=A1sin(x1+φ1)+B1

(4)

G2(x)=A2sin(x2+φ2)+B2

(5)

则：

S≈[a+(φ2-φ1)/2π]·L

(6)

式中，S为位移，L为编码周期。

由于靶标采用固定宽度条码组成，CCD相机一旦获取了靶标图像，其图像像素对应的物理尺寸即确定，而图像的畸变可采用适当图像处理方法进行校正。运用此方法时，CCD相机无需标定。测量过程中，热变形等环境因素对相机外参数的作用将直接影响检测方法的测量精度；而相机内参数的变化对检测方法的测量精度无影响。又由于采用简明的二值化图像处理方法和相位拟合定位方法，靶标图案的照明不均匀性变化对测量精度的影响可得到有效抑制，具有良好的环境适应性和鲁棒性。

4 实验

4.1 实验平台

实验平台包括CCD相机、镜头、光源、支架、靶标以及位移平台。

CCD相机选用Mightex BCD-BG04-U工业相机，其具备分辨率高、检测灵敏度高、低噪声、低功耗和高可靠性等很多优点。镜头选取与相机匹配的COMPUTAR的镜头，该镜头具有很好的分辨率，非常适合对精准度要求比较高的测定。光源采用LED前向多点照射的方式保证光照的均匀性。支架主要是起到固定的作用，确保图像传感器的空间位置不发生任何的相对变动，安装时借助水平仪保证镜头垂直于靶标图案。

为验证本方法的位移检测精度，与大恒光电精密平台GCD-20进行对比试验。GCD-20平台采用GCD-0401电动台控制器，该控制器是一款USB转CAN总线联网通讯的紧凑型控制器，其内部采用高性能CPU芯片控制和驱动电动平移台。该控制器具有上位机自动控制、手动控制、急停和限位、多维顺序、脉冲信号输出等功能，可单独或联网使用，最多支持15路多维级联。GCD-0401控制器可控制GCD-20电动平台运动，同时设定控制器运行参数，其中包括启动速度，启动系数，单步精度等,本实验设置其控制精度为0.001 mm。

使用Mightex BCD-BG04-U工业CCD相机采集靶标图像，通过RS232与计算机通信，计算机上位机驱动程序控制CCD相机参数，并将相机采集的图像进行处理。因实验为准静态环境，曝光时间取100 ms。为获取最优质图像信息，根据靶标与相机镜头之间的距离，设置相机分辨率为640*480。

综合考虑靶标清晰度和制造误差，靶标条码宽度设为1.000 mm，将其固定在直线平移平台上。图7为硬件平台，上位机控制运动平台带动靶标平移，CCD相机采集靶标图像并上传至PC端，上位机对其进行图像处理，提取位移信息。

图7 硬件平台

4.2 实验流程

首先将靶标定位在精密运动平台GCD-20上，通过计算机控制运动平台平移某段固定长度S1。CCD相机采集靶标图像并上传至计算机。使用前文所述的图像处理算法和正弦拟合思想，上位机分析位移前和位移后的靶标图像，计算位移S2，对比S1与S2得出实验误差。

4.3 实验测试

图8为平移前CCD相机采集的靶标图像，控制运动平台平移10.521 mm，图10为平移后采集的靶标图像。

图8 平移前的靶标图像

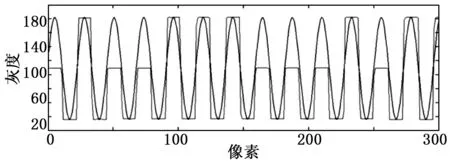
图9 靶标平移前的正弦拟合曲线

靶标编码序列前n位：110100

正弦拟合得到灰度曲线方程:

y1=A1sin(0.2765x+4.7102)+B1

(7)

图10 平移后的靶标图像

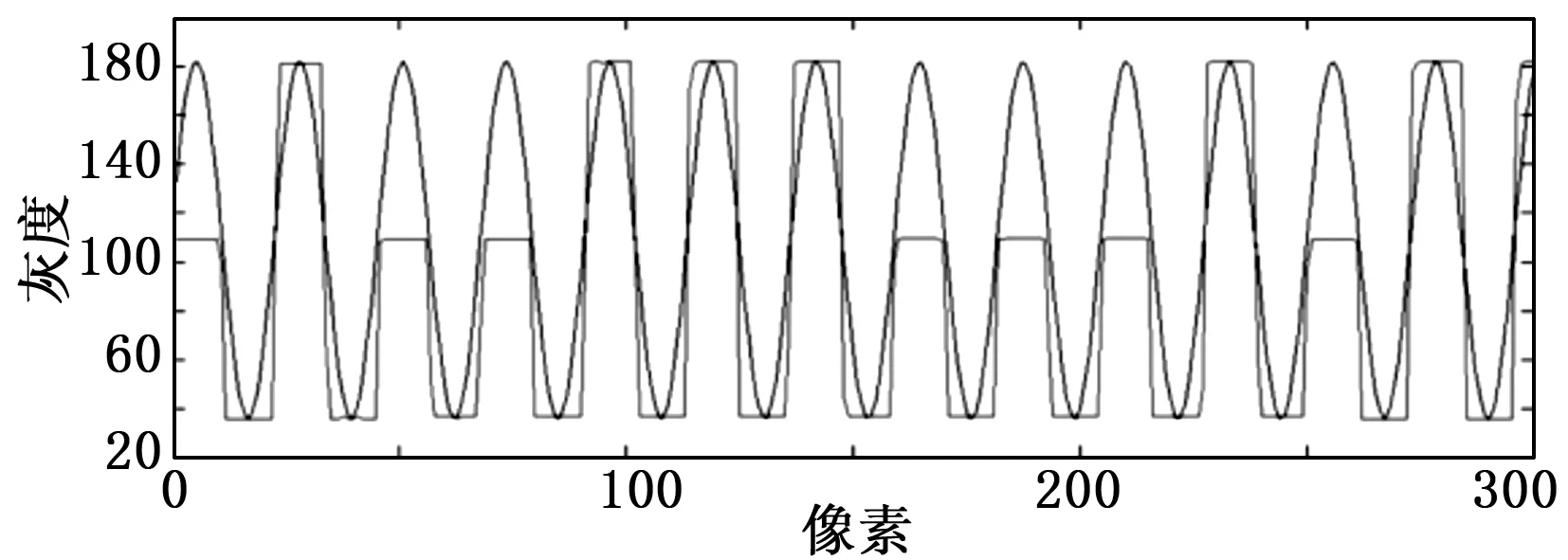
图11 靶标平移后的正弦拟合曲线

靶标编码序列前n位：100111

正弦拟合得到灰度曲线方程：

y2=A2sin(0.2764x+0.06)+B2

(8)

参照图1MLS编码序列相差6位，故a=6；

由式(6)换算位移：S=[6+(0.06-4.7102)/2π]×2=10.519，误差为2 μm。

4.4 重复测量精度

根据上述实验方法，利用GCD-20精密运动平台和本方法作对比测试。选取8组位移，并对每组位移做6次实验来进行重复精度定位。如表1所示，一维精密位移检测误差精度控制在±2 μm，具有可重复性，体现了该实验系统良好的鲁棒性。

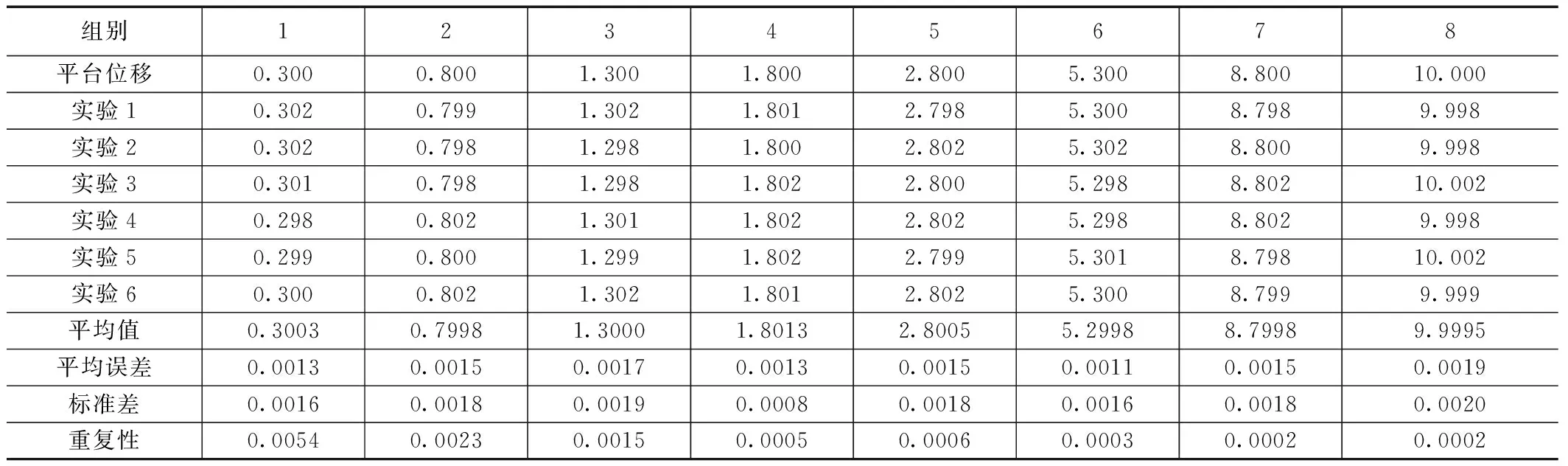
表1 对比测试结果 mm

5 结束语

基于最大长度序列靶标方案，采用机器视觉，实现了高精度一维绝对位移检测。采用二值化和灰度叠加的方法对靶标图像进行处理和绝对位置编码识别，并根据拟合相位提取靶标图像精密位移信息实现了靶标识别和精密位移的检测。一维平移精密检测系统稳定可靠，获得了满意的测量结果和精度，检测精度达±2 μm，并具有可重复性。本方法采用单相机测量，相机无需标定，检测系统结构简单，工作效率高，且环境适应性和鲁棒性良好，具有广阔的应用前景。为进一步提高精度，关于相机失焦、环境温度和光照均匀性等方面的影响值得进一步深入研究。

[1] 于乃功,黄 灿,林 佳. 基于单目视觉的机器人目标定位测距方法研究[J].计算机测量与控制,2012,(10):2654-2656,2660.

[2] 王炜辰. 三维激光测量仪的关键技术研究[D].长春：吉林大学,2015.

[3] Brent Carlson. Geometry Study and Simulation of a Laser-Free Surface Measurement Technique for the Large Adaptive Reflector[R]. 1998.

[4] Orozco B V， Garduo V G. Structured laser light and coordinate measuring systems integration for 3d metrology[A]. Proc. of SPIE[C]. 2005, 5776: 618-629.

[5] 张淑平. 基于视觉的并联机器人位姿检测方法研究[D].上海：东华大学,2010.

[6] 陈若珠,赵 珊. 基于机器视觉技术的振动台试验变形位移测量方法研究[J]. 计算机测量与控制,2016,24(6):56-59.

[7] 张子淼,王 鹏,孙长库. 单目视觉位姿测量方法及数字仿真[J]. 天津大学学报,2011,(05):440-444.

[8] Hirata SeiichironakajimaNobuoidaShogohojoHarumas. Ultra-sensitive system for measuring distance or position [P]. 国外专利:WO2011043091,2011-04-14.

[9] 唐恒博. 轨道机器人的高鲁棒定位方法[D].上海:上海交通大学,2013.

[10] 王 阳. 基于单码道绝对位置编码的光电式轴角编码器[D].北京:北京交通大学,2007.

[11] 杨德华, 费 飞, 李开宇,等. 一种基于视觉的位置检测编码靶标及系统 [P].中国专利：201510201768.X, 2015-04-24.

[12] Johnson N, Mohan K J, Janson K E,et al.Optimization of incremental optical encoder pulse processing[A]. 2013 International Mutli-Conference on Automation, Computing, Communication, Control and Compressed Sensing (iMac4s)[C]. 2013: 769-773.

[13] Zago L，MirsadSarajlic， Chevalleya F，et al. Metrology system for the calibration of multi-dof precision mechanisms[A]. Modern Technologies in Space- and Ground-based Telescopes and Instrumentation II[C].2012.

[14] 周文举. 基于机器视觉的在线高速检测与精确控制研究及应用[D].上海:上海大学,2014.

[15] 张浩鹏. 视觉检测系统的若干关键问题研究[D].哈尔滨:哈尔滨工程大学,2013.

[16] 李 徽，杨德华，翟 超. 六自由度机构位姿的单相机照相测量研究. [J] 光学技术, 2010，36(3)：344-349.

Precision Displacement Detection Method Based on Maximum Length Sequence

Li Qiang，Yang Dehua，Fei Fei，Wang Jingdong，Wang Haitao

(College of Automation Engineering, NUAA, Nanjing 210016, China)

In order to detect the tiny displacement of the precision mechanism, according to the theory of displacement coding and machine vision technology,the MLS-based visual target schemes are figured out. Based on the algorithms of gray superposition and image binarization,the image of visual targets is processed and the target absolute position is then recognized. Further, the precise positioning is studied based on a phase-fitting method, and thereby, the precision measurement of one-dimension absolute displacement is realized with experimental verification carried out. The preliminary experiment results confirms that the MLS-based absolute displacement detection method is effectively capable for one-dimension absolute displacement detection with a positioning accuracy falling in the range of ±2 μm, and exhibits excellent repeatability and robustness, as well as the sound advantage of being free of visual calibration of the CCD camera.

maximum length sequence; absolute displacement detection; vision detection; gray level; sine fitting; phase

2017-02-23；

2017-04-02。

国家自然科学基金项目(U1531110)。

李 强(1988-)，男，湖北荆州人，硕士研究生，主要从事光电精密检测方向的研究。杨德华(1973-)，男，安徽当涂人，教授，硕士研究生导师，主要从事精密检测方向的研究。

1671-4598(2017)08-0032-04

10.16526/j.cnki.11-4762/tp.2017.08.009

TH741

A