针对SIFT及其变体的图像匹配性能比较

栾广宇，黄操军，陈争光，曹洪军

针对SIFT及其变体的图像匹配性能比较

栾广宇，黄操军，陈争光，曹洪军

（黑龙江八一农垦大学信息技术学院，大庆 163319）

由于尺度不变特征变换算法（SIFT）及其变体（PCA-SIFT、GCSIFT、SURF、ASIFT）在图像匹配应用的广泛性，总结各自特点及比较它们性能具有实际的意义。首先系统地分析了SIFT及其变体，然后在尺度和旋转变化、光照变化、模糊变化、仿射变化四种图像情况评估了它们的性能。实验结果表明在尺度和旋转变化上SIFT执行最好；在光照和模糊变化上GCSIFT执行最好；在仿射变化上ASIFT表现最好；在所有情况下PCA-SIFT性能总是第二和SURF性能最差。

特征匹配；SIFT；PCA-SIFT；GCSIFT；SURF；ASIFT

图像匹配的目的是寻求同一场景的两幅图像特征之间的对应关系。在实际应用中，两幅图像之间存在着平移、尺度、旋转、亮暗、视角等差异，这给图像匹配算法带来了挑战性。许多国内外研究人员都在专注图像匹配的性能改善，并提出了各种算法[1-3]。基于特征的图像匹配算法可分为全局特征的匹配算法和局部特征的匹配算法，并广泛地被应用于许多领域，如农业机器人采摘、运动跟踪、对象识别等。相对于全局特征匹配算法，局部特征匹配算法具有更好的稳定性。局部特征匹配算法包括特征的检测和描述两部分。特征检测应具备高重复率特征和快速检测，而特征描述应具备低维数描述。1999年David G.Lowe在尺度空间理论基础上提出了局部特征描述算法 SIFT （Scale invariant feature transform）[4-5]。SIFT算法主要包括关键点检测、描述符建立、特征匹配三步骤。该算法具有良好的稳定性和不变性，并且其局部关键点包含大量的信息。由于它的独特优势，许多研究人员主要改善描述符建立和关键点检测来提高其性能。从描述符建立角度，SIFT使用了128维向量来描述每个关键点，而这种高维度会使特征匹配速度很慢。2004年Y.Ke[6]采用主成分分析法代替SIFT中的直方图方法。这种改进的方法被称为PCASIFT（Principal component analysis SIFT），该算法减少了描述关键点的维数。另外，SIFT仅考虑局部信息而忽略了全局信息。2005年E.N.Mortensen[7]提出了带全局纹理的SIFT描述符，即GCSIFT（Global contextSIFT）。从关键点检测角度，2006年H.Bay[8]提出了SURF（Speeded up robust features），其非常相似 SIFT但它的每步采用不同的方法，即SIFT的增强版。2009 年 J.M.Morel[9]提出了 ASIFT（Affine SIFT），其采用仿射变换参数。对SIFT及其最为关注的四个变体进行了较为深入地分析。为了评估它们的性能，我们在不同的情况下进行实验，比较其匹配正确率。最后我们讨论了它们各自优缺点。

1 SIFT及其变体

1.1 SIFT算法

对于图像匹配，SIFT算法所提取的特征点具有尺度和旋转不变性。为了实现尺度不变性，SIFT利用高斯差分函数作卷积，这样就得到了不同尺度图像：

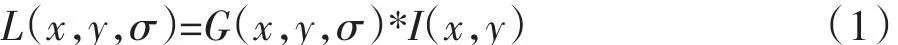
式中 I（x，y）表示输入图像，G（x，y，σ）是尺度可变高斯函数，σ为尺度因子。然后，同一分辨率下相邻图像相减得到高斯差分金字塔。高斯差分函数是一种对高斯拉普拉斯算法的改进：

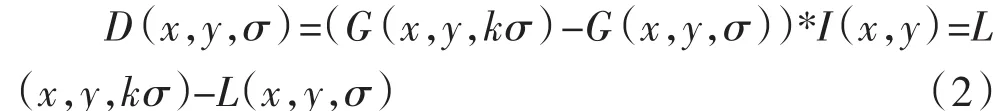
其中k表示同一组相邻两层尺度值的比例系数。每个点与其邻近的26个像素进行比较，该26个像素包括同层的8个相邻像素和上下相邻层的9个像素。如果点是最小值或最大值，则该点的位置和尺度被保留下来。这样，就可以得到高斯差分尺度空间的所有极值点及其位置。然后去掉低对比度和不稳定的边缘点，在每个局部极值点的尺度下，SIFT计算其邻域的梯度模和方向：

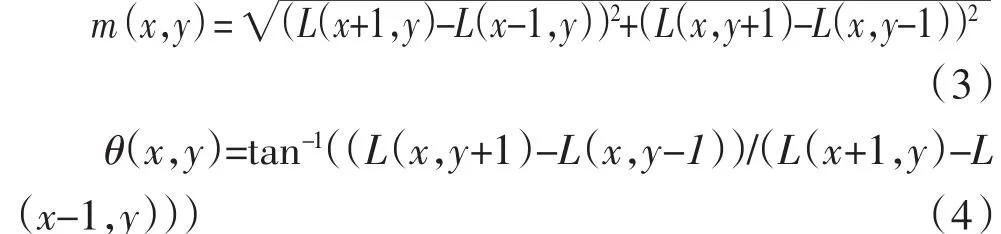
SIFT利用梯度方向直方图统计邻域内像素的梯度信息，并将0°～360°的邻域梯度直方图划分成36柱。关键点的主方向被定义为直方图的峰值。然后，SIFT以关键点为中心选择一个16×16区域。将这个区域划分为4×4的子区域并求和每个子区域的梯度强度。SIFT利用每个子区域的8个方向产生一个8维向量。因此，SIFT从这16个子区域得到一个128维特征。

1.2 PCA-SIFT算法

主成分分析（PCA）是一种有效地和广泛地被使用的数据降维技术。它利用正交变换将原始相关的随机矢量转化为一个不相关的新随机矢量。PCASIFT利用PCA替代SIFT的梯度直方图方法。它的描述过程被分为投影矩阵产生和描述符建立两个子步骤。在降维的过程中，一个输入矢量在关键点为中心的41×41邻域里有水平和垂直两个方向的梯度映射，可生成一个2×39×39=3 042维向量。在投影矩阵产生后，计算PCA-SIFT的描述符。这样就产生一个新的矢量，其比SIFT的矢量小很多。

1.3 GCSIFT算法

GCSIFT将全局纹理信息引入SIFT，这样可获得大范围曲率形状信息的描述器。对于每个被检测的关键点，建立一个向量。该向量由局部特征的SIFT描述器和全局纹理向量两部分组成。其关键点描述子通常地为188维。该全局纹理向量用于区分相似局部特征。GCSIFT的向量数学表达式：

其中L是SIFT的128维向量，G是60维全局向量，ω是相对权重系数。相似于SIFT局部描述器的产生，全局纹理也由直方图产生。GCSIFT需要计算每个像素的最大曲率，该最大曲率被定义为海森矩阵的最大绝对特征值。GCSIFT建立每个关键点的对数极坐标并将一个以图像对角线的长度为直径的圆分成多个区域，再计算每个关键点的角度和径向距离的离散值。这样，就计算出一个曲率图像。

1.4 SURF算法

SURF的基本思路类似SIFT，但SURF使用不同的方法来定位检测和描述符生成。由于图像数据库中存在大量的数据，并且SIFT耗时很高，Bay提出SURF来提高极值点的检测和描述效率。其使用Hessian矩阵进行检测，可具有一定的速度和精度的优势。Hessian矩阵判别局部极大值：

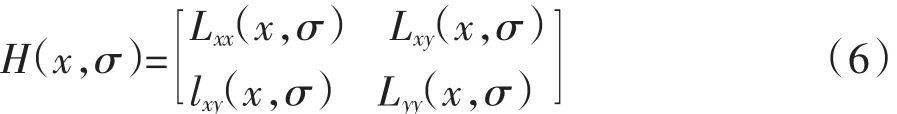
式中Lxx（x，σ）、Lxy（x，σ）和Lyy（x，σ）表示特征点在x点和y点处二阶高斯偏导数。同时，采用一种积分图像算法代替SIFT高斯金字塔的构造。在描述阶段SURF将每个极值点的邻域划分为多个4×4子区域，再计算每个子区域的Haar小波响应。每个响应都有一个4维向量。这样，所有子区域的64维特征描述每个关键点。

1.5 ASIFT算法

SIFT对于仿射变化图像不能执行很好。为了改善这种情况的性能，ASIFT模拟摄像机光轴旋转，并根据视点变化采用一个图像仿射变换模型，其表达式为：

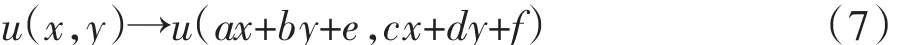
在上述的仿射模型中，假设相机是远离被测对象。从另一方面，相机的运动可能会导致被测对象的成像变形。经度角产生于被测对象的法平面和相机光轴的映射平面。ASIFT增加旋转变换的图像，再根据 x 方面上倾斜变换操作 u（x，y）→u（tx，y）得到一系列仿射图像。通过改变一定范围的经度角和纬度角，可实现旋转变换和倾斜变换。然后，ASIFT检测关键点，并建立仿射图像描述。在匹配阶段，对比SIFT，ASIFT不仅检测更多的特征点而且也有相对较少的误匹配点。

2 实验结果与分析

为了测试 SIFT、PCA-SIFT、GCSIFT、SURF、ASIFT五种算法的性能，针对尺度和旋转变化、光照变化、模糊变化、仿射变化四种图像情况，采用Mikolajczyk数据库（http：//www.robots.ox.ac.uk/～vgg/data/data-aff.html）。

2.1 尺度和旋转不变性的比较

第一组实验对象是“Boat”的6幅图像，该组图像给出6幅不同尺度和旋转的图像。图1（a）、（b）给出了“Boat”的第1幅和第6幅图像。实验进行第1幅图像与其他各幅图像匹配。图1（c）给出了第1幅与其他5幅之间五种算法的匹配正确率。从图1（c）可知，PCA-SIFT、SIFT在第 2、3幅上具有相同的性能，PCA-SIFT在第6幅上执行最好，SIFT保持基本一致。而GCSIFT和ASIFT具有较低的匹配率，ASIFT的匹配正确率对于第6幅是最低的。SURF的匹配结果基本上是最差的。

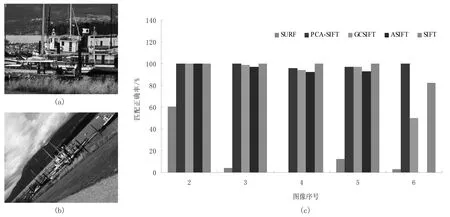
图1 尺度和旋转“Boat”数据的匹配对比实验（a）第1幅图像（b）第6幅图像（c）第1幅与其他5幅之间五种算法的匹配正确率Fig.1 Matching experiment of“Boat” data under scale and rotation variance（a） the first image（b） the sixth image（c）the matching correct rate of the five algorithms between the first image and the other five images respectively

2.2 光照不变性的比较

第二组实验对象是“Leuven”的图像，Mikolajczyk数据库的“Leuven”图像是以第3幅图像为原始图像，并用该幅图像通过增加和减少亮度产生8幅不同的亮度图像。 图 2（a）、（b）给出了“Leuven”原始图像的亮度增加图像（+50）和亮度减少图像（-50）。 图 2（c）给出了原始图像与其产生的8幅之间五种算法的匹配正确率。从图2（c）可知，这五种算法的结果在无亮度变化时是最好的，并且他们的结果随着亮度增加和减少呈下降趋势。GCSIFT、PCA-SIFT、SIFT的匹配结果很相似。ASIFT和SURF执行得都不好。

2.3 模糊不变性的比较

第三组实验对象是“Bike”的图像，Mikolajczyk数据库的“Bike”图像是以第1幅图像为原始图像，并用该幅图像通过模糊半径产生8幅不同的模糊图像。图 3（a）、（b）给出了“Bike”的原始图像和第 8 幅模糊图像。实验进行原始图像与其产生的8幅图像匹配。图3（c）给出了原始图像与其产生的8幅之间五种算法的匹配正确率。从图3（c）可知，这五种算法的结果基本上都呈现下降趋势。GCSIFT、PCA-SIFT具有相当的性能。SURF的匹配率始终是最差的。

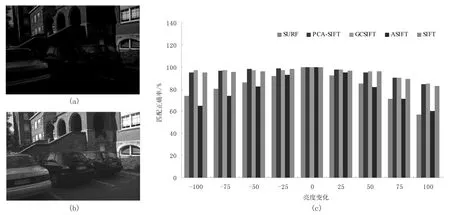
图2 光照“Leuven”数据的匹配对比实验（a）原始图像的亮度增加图像（+50）（b）原始图像的亮度减少图像（-50）（c）原始图像与其产生的8幅之间五种算法的匹配正确率Fig.2 Matching experiment of“Leuven” data under illumination variance（a） the illumination image increasing 50 brightness intensity from the original image（b） the illumination image decreasing 50 brightness intensity from the original image（c）the matching correct rate of the five algorithms between the original image and the 8 generated images respectively

图3 模糊“Bike”数据的匹配对比实验（a）原始图像（b）第8幅模糊图像（c）原始图像与其产生的8幅之间五种算法的匹配正确率Fig.3 Matching experiment of“Bike” data under blur variance（a） the original image（b） the eighth generated blur image（c）the matching correct rate of the five algorithms between the original image and the 8 generated images respectively

2.4 仿射不变性的比较

第四组实验对象是“Graffiti”的图像，该组图像给出 6 幅不同仿射的图像。 图 4（a）、（b）给出了“Graffiti”的第1幅图像和第6幅图像。图4（c）给出了第1幅与其他5幅之间每种算法的匹配正确率。从图4（c）可知，ASIFT的匹配正确率在各个角度都是最好的， 接着是 PCA-SIFT和 SIFT。SIFT、PCA-SIFT、GCSIFT、ASIFT对于小于30度的视点角度变化都能执行很好，而且随着角度变化的增大，它们的性能开始下降。对于小于40度的视点角度变化SURF是最差的，而对于大于50度的视点角度变化SURF比SIFT、PCA-SIFT、GCSIFT 都好。

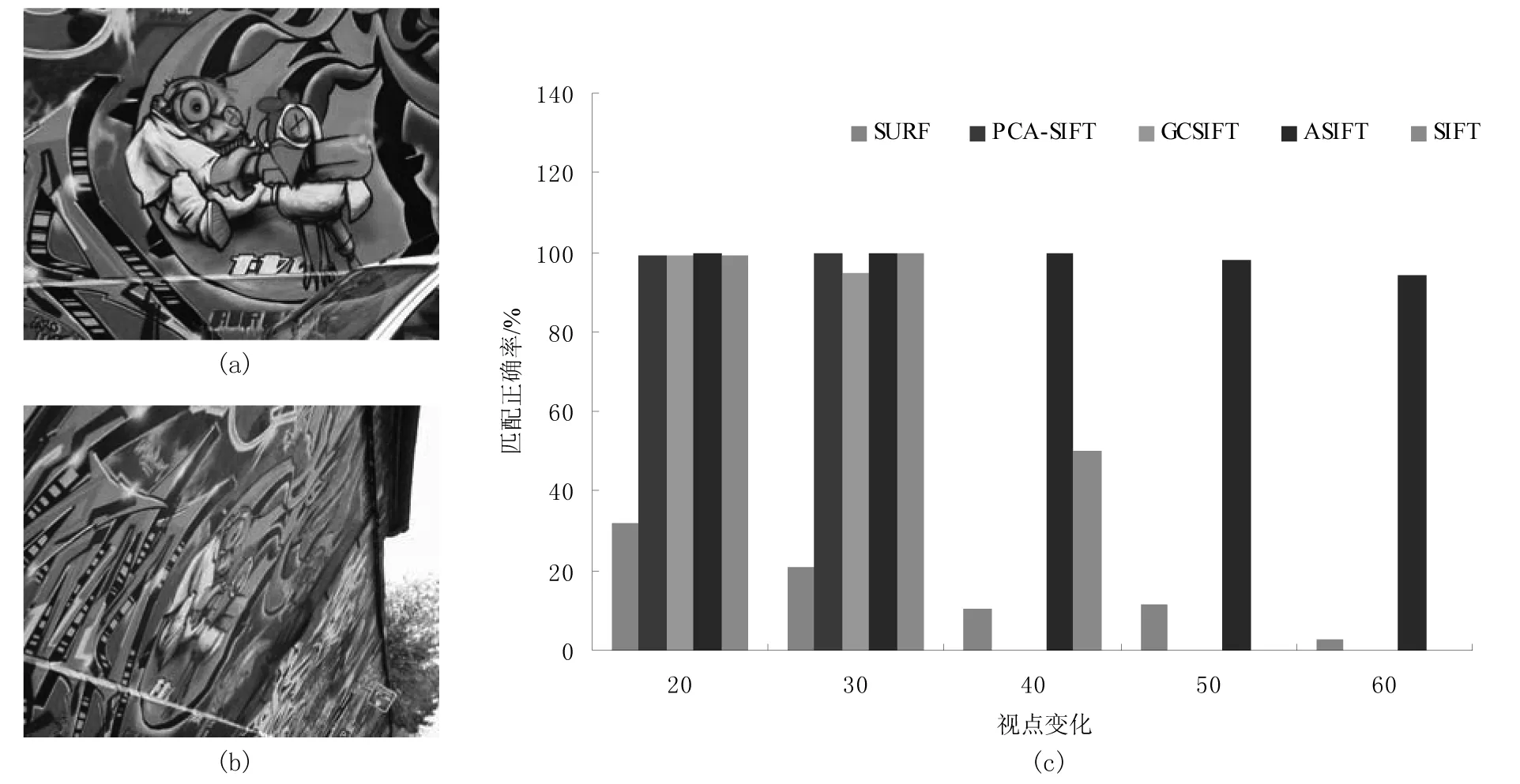
图4 仿射“Graffiti”数据的匹配对比实验（a）第1幅图像（b）第6幅图像（c）第1幅与其他5幅之间每种算法的匹配正确率Fig.4 Matching experiment of“Graffiti”data under affine variance（a） the first image（b） the sixth image（c）the matching correct rate of the five algorithms between the first image and the other five images respectively

3 结论

系统地分析了基于尺度空间的图像局部特征五种算法：SIFT、PCA-SIFT、GCSIFT、SURF、ASIFT。在不同的实验情况下评估了它们的性能：SIFT在尺度和旋转变化上表现最好，GCSIFT在光照和模糊变化上表现最好，ASIFT在仿射变化上表现最好，PCA-SIFT在所有情况下性能总是第二和SURF在所有情况下性能最差，从而可用于选择不同情况的最佳算法。

［1］ 白廷柱，侯喜报.基于SITF算子的图像匹配算法研究［J］.北京理工大学学报，2013，33（6）：622-627.

［2］ 袁修孝，陈时雨，张勇.利用PCA-SIFT进行特殊纹理航摄影像匹配［J］.武汉大学学报，2016，41（9）：1137-1144.

［3］ 朱焕，马文静，盛永生，等.多尺度各向异性小波收缩图像分割算法在玉米病斑特征提取时的应用［J］.黑龙江八一农垦大学学报，2016，28（2）：136-140.

［4］ Lowe DG.Object recognition from local scale invariant features［C］//In Proceedings of the 7th IEEE International Conference on Computer Vision，1999，IEEE，2：1150-1157.

［5］ Lowe DG.Distinctive image features from scale-invariant keypoints［J］.International Journal of Computer Vision，2004，60（2）：91-110.

［6］ Ke Y，Sukthankar R.PCA-SIFT：A more distinctive representation for local image descriptors［C］//In Computer Vision and Pattern Recognition（CVPR 2004），2004，IEEE，2：506-513.

［7］ Mortensen EN，Deng H，Shapiro L.A SIFT descriptor with global context ［C］//In ComputerVision and Pattern Recognition（CVPR 2005），2005，IEEE，1：184-190.

［8］ Bay H，Tuytelaars T，Gool LV.SURF：Speeded up robust features［C］//In Computer Vision-ECCV 2006：9th European Conference on Computer Vision，2006，Springer，Part II：404-417.

［9］ Morel J M，Yu G.ASIFT：A new framework for fully affine invariant image comparison［J］.SIAM Journal on Imaging Sciences，2015（2）：438-469.

Performance Comparison of SIFT and its Variants for Image Matching

Luan Guangyu，Huang Caojun，Chen Zhengguang，Cao Hongjun
（Heilongjiang Bayi Agricultural University，Daqing 163319）

Due to strong ability of SIFT and its variants （PCA-SIFT，GCSIFT，SURF and ASIFT） for image matching，that summarizing their characteristics and comparing their performance is meaningful.This paper first systematically analyzes SIFT and its variants.Then，it evaluates their performance of the five algorithms in different situations that are scale and rotation change，illumination change，blur change and affine change.The experimental results show SIFT performs the best under scale and rotation change，GCSIFT performs the best under illumination change and blur change，ASIFT performs the best under affine change，PCASIFT is always the second and SURF performs the worst in different situations.

feature matching;SIFT;PCA-SIFT;GCSIFT;SURF;ASIFT

TP391

A

1002-2090（2017）05-0106-05

10.3969/j.issn.1002-2090.2017.05.025

2016-11-26

黑龙江省教育厅科学技术研究项目（12541584）。

栾广宇（1978-），女，讲师，哈尔滨工业大学毕业，现主要从事电气工程、图像处理、自动化检测等方面的教学与研究工作。