高速公路凹形竖曲线路段防眩设施高度计算及应用

赵晓娟

（山西省交通科学研究院，山西 太原 030006）

0 引言

眩光是指因视野中亮度分布不适宜，或在空间、时间上存在极端的亮度对比，从而引起视觉不舒适和可见度降低的视觉条件[1]。有关资料统计表明，眩光是导致夜间行车安全的一个重要因素。因此，防眩问题受到了越来越多的关注。特别是在公路纵坡较大、竖曲线半径较小的凹形竖曲线路段夜间行车交通安全隐患极大，其主要原因为防眩高度不足。

在防眩高度研究方面，我国《公路交通安全设施设计》（JTG/T D81—2006）[2]根据不同车型组合提出了直线路段防眩设施高度的计算公式；肖代全[3]等计算了不同道路横断面和交通组成条件下的防眩植物高度，并利用几何方法推导出凹曲线路段防眩植物的高度修正值；孟利强[4]从理论上提出在凹竖曲线路段应采用较高大植树防眩，增加防眩设施高度的解决方案；杨建江[5]等人从道路纵断面建立空间数学模型，推导出高速公路凹、凸曲线防眩板高度函数，但是其公式推导前提是相向两车均处在最内侧车道，这与实际的最不利情况有所偏差。

从当前研究看，防眩高度研究一是没有考虑最不利车道与车型组合情形或者考虑有所偏差，二是研究条件为发出眩光车辆与受眩光影响车辆同时出现在凹曲线内，并未考虑平直路段与凹曲线的衔接部分。基于此本文首先通过分析平直路段防眩最小高度，推导出最不利车道组合与车型组合。然后在最不利车道、车型组合条件下，根据发出眩光车辆、防眩设施位置、受眩光影响车辆3点是否在凹曲线内，建立了一般意义下的凹曲线防眩高度计算模型。最后通过实例分析，计算需要修正防眩高度的凹曲线半径临界值，为高速公路防眩设施设计提供了理论依据。

1 平直路段防眩高度

在平直路段，防眩设施的最小高度可按驾驶员刚好不受对向车道眩光影响这一几何关系进行计算。由图1可推算：

式中：H为防眩高度，m；h1为汽车前照灯高度，m；h2为驾驶员视线高度，m；B1、B2分别为车行道上车辆距防眩设施中心线的距离，m，B=B1+B2。

在平直路段，前照灯越高，越容易照射到对向车道，驾驶员视线高度越高，越容易受到眩光影响，因此从车型组合的角度来看，最不利的情况是大型车车灯导致的大型车驾驶员眩光。另一方面，由式（1）可知，在h1、h2确定的情况下，防眩高度取决于B1/B的大小，也就是说眩光源车辆距道路中线越远，受眩光车辆距道路中线越近，对防眩高度的要求越高。但根据《公路交通安全设施设计》[2]，相会两车横距（B）达到14 m时，相会两车的灯光不会使驾驶员产生眩目影响。由《公路路线设计规范》（JTGD20—2006）[6]可知，当眩光源车辆位于3车道，受眩光车辆位于1车道时，两车横距一般为14～16 m，此时无眩光影响。因此在确定防眩设施高度时，需考虑的最不利情况为1车道上的大型车驾驶员受对向位于2车道上大型车车灯的眩光。

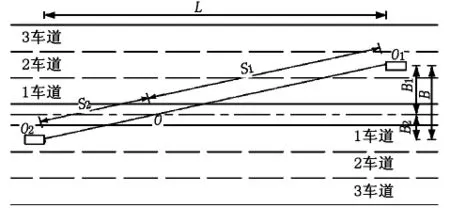
图1 平直路段防眩平面示意图

设车道宽度为a，中间带宽度为b，假设车辆在行车道中线行驶，由图1可知，

式中：S1为眩光源车辆与防眩设施直线距离，m；S2为受眩光影响车辆与防眩设施直线距离，m；k为常数。

将式（2）代入式（1），防眩高度H为：

2 凹形竖曲线防眩高度

凹曲线一般分为圆曲线和抛物线两种，根据《公路路线设计规范》（JTG D20—2006）[6]的推荐，本文取抛物线作为研究对象。下面以竖曲线起点为原点建立坐标系，分两种情形（两车均位于凹形竖曲线内和1辆车位于凹形竖曲线内）确定竖曲线内任意一点O的防眩高度。

2.1 情形一 两车均位于凹形竖曲线内

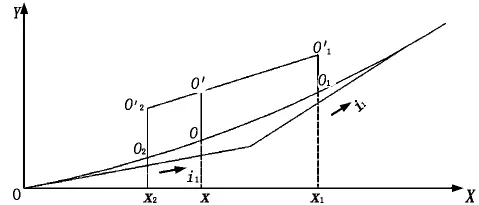
图2 凹形竖曲线路段防眩高度模型

如图2所示。x为竖曲线上任意一点O在坐标系中X轴上的投影值；x1、x2分别为发出眩光大型车与受眩光影响大型车在X轴上的投影值。根据竖曲线上任一点的高程改正值计算公式，O1、O2的纵坐标为：

若一个项集中包含多个关系的项，其频数的定义一般会被定义为项集在连接后的查询表中的出现次数。这种定义方式很容易导致统计偏斜问题。

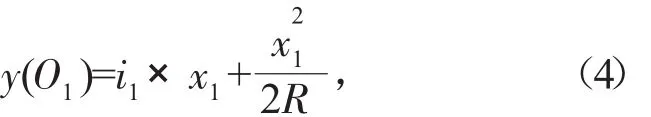
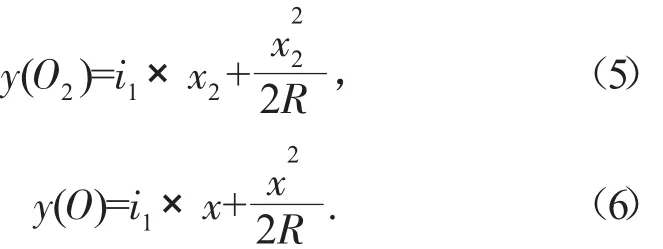
O1'、O2'的纵坐标为：

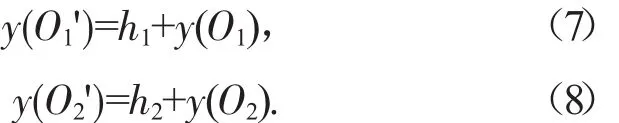
式（4）～（8）中：R 为竖曲线半径；y(O1)为受眩光影响大型车在竖曲线上的纵坐标；y(O2)为眩光源大型车在竖曲线上的纵坐标；y(O)为防眩设施在竖曲线上的纵坐标；y(O1')为大型车驾驶员视线的纵坐标；y(O2')为大型车车灯的纵坐标。

由图2可推出：

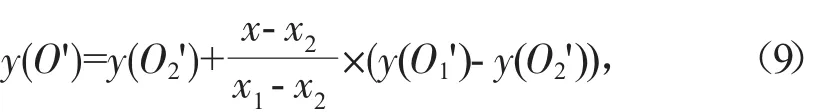
由式（2）可得：

则防眩高度H为：

2.2 情形二 一辆车位于凹形竖曲线内

当受眩光大型车（或发出眩光大型车）位于直坡段，所求点O位于竖曲线时；

防眩高度H为：

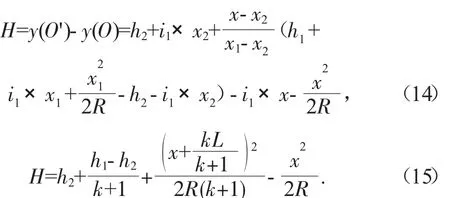
当受眩光大型车（或发出眩光大型车）与所求点O位于直坡段，发出眩光大型车（受眩光大型车）位于竖曲线时，

防眩高度H为：

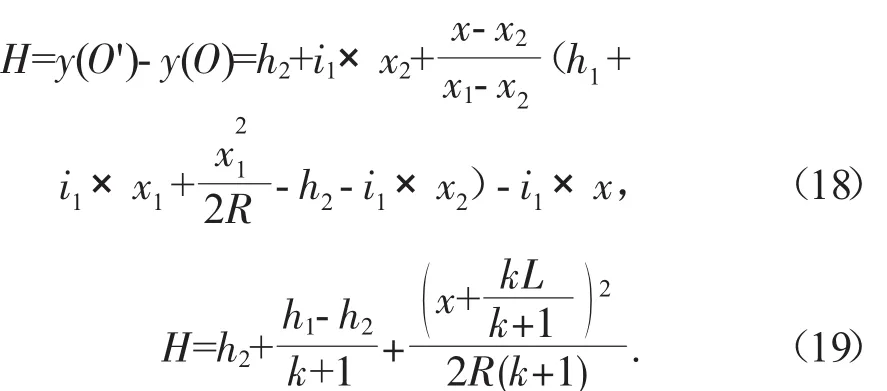
3 应用研究

以山西某双向四车道高速公路（设计速度采用80 km/h，路基宽度24.5 m）其中一段凹曲线为例，中间带宽3 m，车道宽3.75 m，竖曲线半径为7500 m，前后纵曲线的坡度分别为-3.2%和2.1%。按照前述计算方法，普通路段防眩高度H=1.678 m。

应用前述计算公式，以竖曲线起点为坐标原点，通过MATLAB建立计算模型，得到竖曲线及竖曲线前后各点防眩结果图，见图3。

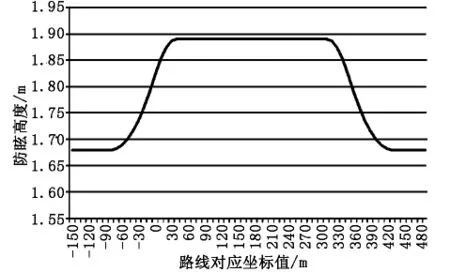
图3 凹形竖曲线路段防眩高度

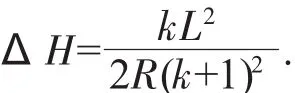
令ΔH≤0.122时，凹曲线路段与平直路段统一设置高度为1.7 m的防眩设施。也就是说，凹形竖曲线的临界半径值为12870 m，当凹形竖曲线半径R≤12870 m时，防眩设施高度需要进行高度修正设计。需要注意的是，在平直路段与需要进行高度修正的凹曲线路段之间，应设置渐变过渡段，避免突变给驾驶员造成不适。根据《公路交通安全设施设计》[2]，同时为方便产品加工以及施工安装，可将防眩设施按0.05 m的高度间隔采用50 m的过渡段长度进行过渡。

4 结论与建议

a）本文首先通过分析平直路段防眩设施最小高度，推导出高速公路（不论车道数）平直路段基于道路横断面的防眩设施高度计算公式以及最不利车道与车型组合。

b）在最不利车道与车型组合条件下，根据发出眩光车辆、防眩设施位置与受眩光影响车辆3点是否在凹曲线内，建立了一般意义下的凹曲线防眩高度计算模型，并且推导出相应的防眩高度计算表达式。

c）凹形竖曲线路段防眩高度的变化规律为从凹形竖曲线前开始逐渐增大，然后保持不变，最后又逐渐减小到普通值。

e）在平直路段与需要进行高度修正的凹曲线路段之间，可将防眩设施按0.05 m的高度间隔采用50 m的过渡段长度进行过渡，避免突变给驾驶员造成不适。

f）本文从纵断面角度进行了防眩高度的研究与应用，对平曲线路段以及平纵组合路段的防眩高度以及效果有待进一步研究。