基于遗传BP神经网络反演楔体参数的研究

张雨，贾静，韩庆邦，姜学平，单鸣雷，朱昌平



基于遗传BP神经网络反演楔体参数的研究

张雨，贾静，韩庆邦，姜学平，单鸣雷，朱昌平

(河海大学物联网工程学院，江苏常州213022)

为了获得未知楔体的参数，建立了遗传算法和反向传播(Back Propagation，BP)神经网络结合的反演模型。仿真得到不同角度、密度、杨氏模量下楔体导波的频散曲线。采用反对称第一阶模态相速度数据作为遗传BP神经网络反演模型的输入变量；利用遗传算法改进BP神经网络获得优化的初始权值和阈值，并对BP神经网络进行训练；最后将实测的楔体一阶模态相速度代入训练好的网络进行参数反演。结果表明，通过该反演模型可同时反演出楔体的角度、密度、杨氏模量，并且较单一BP神经网络具有收敛速度快、精度高的优点。

反演；楔体导波；频散；BP神经网络；遗传算法

0 引 言

楔形零件在生产和生活中十分常见，例如斜面垫块、斜面压块、金属楔子等。图1为简化的楔体模型。由于外部压力和使用环境湿度、温度的变化，楔体的尖端会产生磨损，引起楔尖角度的变化，楔体的锈蚀也会对楔体零件的质量产生影响。确定楔形零件的角度以及材料参数，及时更换相同型号的楔体零件对于保障工业生产的安全具有十分重要的意义。

楔体弹性导波，简称楔波，是由Lagasse等[1]通过数值模拟发现的沿着楔体顶端传播的导波。楔波的传播方向如图1所示，在理想的无限尖的楔体中，楔波主要以对称模态和反对称模态存在。其中反对称模态综合了Lamb波和Rayleigh波的特性，其相速低(相速度远小于Rayleigh波速度)、能量集中在楔尖以及频散等特征使其在无损检测与评价等方面具有很好的应用[2]。受楔体结构的影响，楔波在传播过程中会形成多模态和频散，频散特征是对楔体结构进行评估和检测的重要标准。目前关于楔波的频散只有一些近似理论和数值模拟工作，还没有基于弹性力学的确切解。

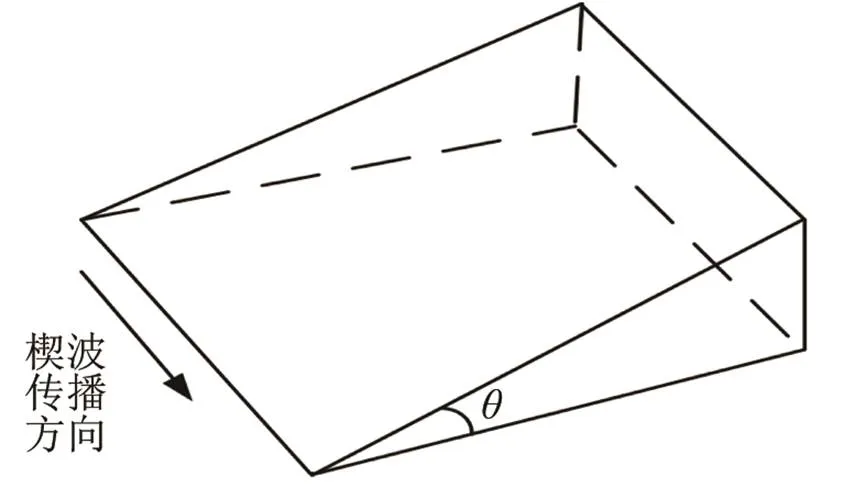
图1 简化楔体模型

楔波的频散隐含楔体的角度、材料参数等信息，但是近似理论不能建立两者之间的联系，使用近似理论得到的频散反演楔形零件的角度、材料参数具有较大的难度。

人工神经网络具有极强的容错性、自组织和泛化能力。它是一种“黑匣”式的映射，无需明确两者间的确切关系，非常适合解决非线性复杂问题[3]。将楔波的第一阶模态相速度作为神经网络的输入，对应的角度、材料参数作为输出训练网络，训练好的网络可以用来解决楔体参数的反演。单一的神经网络具有收敛速度慢、训练时间长、精度低的缺点[4]。本文使用遗传算法对神经网络进行改进。利用遗传算法对神经网络的权值、阈值进行优化，采用优化后的权值、阈值对神经网络进行训练，建立遗传BP神经网络反演模型。最后，将实验结果代入反演模型，得到实验楔体的角度、密度、杨氏模量。该结果可以为研究楔体的参数对楔波频散的影响提供理论依据。

1 楔波频散特性

现有的关于楔波的理论只有McKenna提出的薄板近似理论[5]和Krylov的几何声学近似理论[6]。Mckenna将楔体看成厚度不均的薄板，对理想楔体进行了研究，但是该近似理论不适用于大角度楔体的计算。Krylov的几何声学理论估算了理想的无限尖的楔体中楔波的相速度的近似关系，其结果表明沿楔尖方向传播的楔波模态数目及其传播速度均依赖于楔尖角度，楔尖角度越小，可传播的楔波模态数量越多。但是几何声学理论对于楔波的一阶模态不适用。

Lagasse使用数值计算方法计算了无限大理想楔体的相速度与楔尖角度的关系，并给出了相速度经验公式如式(1)所示[1]。

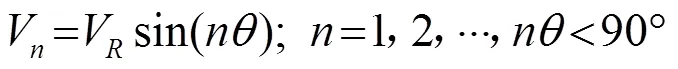
Lagasse给出的经验公式是无频散的，实际中，楔体不可能做到无限尖，另一方面楔体顶端或多或少会出现一些缺陷，这些都会使楔波在传播过程中产生频散，此时使用经验公式是不准确的。但是根据Lagasse的经验公式，可以估计楔波的模态数，相速度和楔尖角度、材料参数的关系。据此可以建立一阶模态相速度和材料参数的正演关系式：

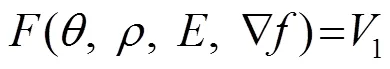
根据建立的正演公式使用COMSOL软件进行仿真，获得不同参数下楔波的频散。图2是仿真楔体楔尖为=24°、密度=7 800 kg/m3、杨氏模量=190 Gpa、6 μs时刻楔尖沿轴方向的位移变化。沿楔波传播方向取点阵列，得到时间位移矩阵。对矩阵进行二维傅里叶变换[7]，即可得到如图3所示楔波的频散曲线。图3的频散曲线包含三个模态；A1A2A3模态，A1为楔波的反对称第一阶模态。

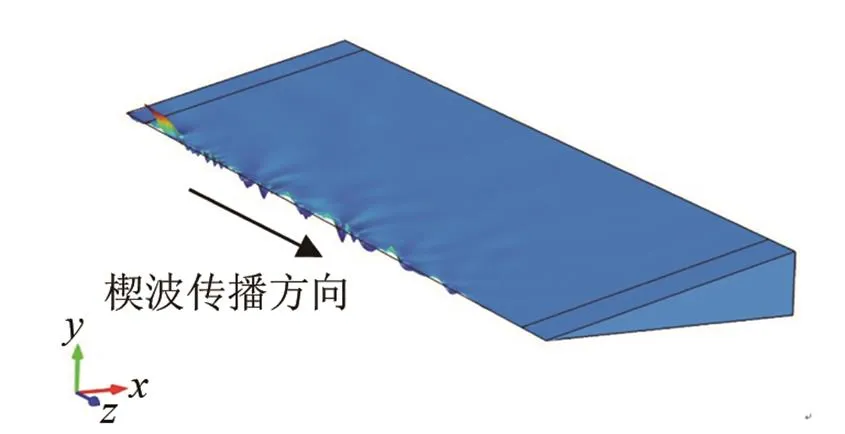
图2 仿真模型6 μs时刻的楔尖位移

Fig 2 The displacement of wedge tip at the time of 6 μs in simulation

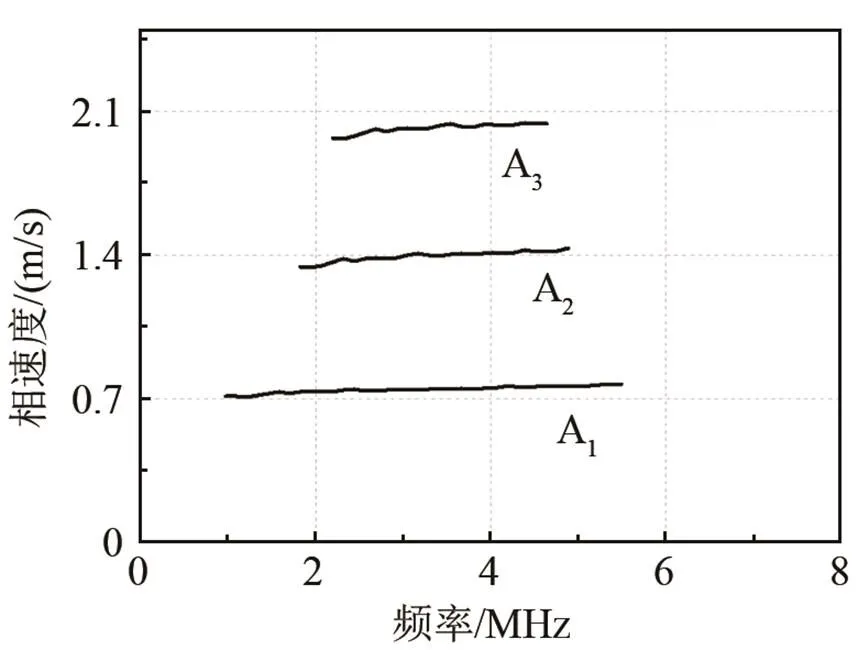
图3 仿真模型频散曲线

本文的研究目标是由频散曲线反演得出楔体参数，即通过1得到楔体的三个参数、。仿真不同参数下的楔体，得到楔波反对称第一阶模态相速度数据集作为输入，对应的楔体参数集作为输出，训练遗传BP(Back Propagation)神经网络，即可得楔体参数和第一阶模态相速度之间的关系。对实验样品进行楔波一阶频散相速度的提取，代入到训练好的遗传BP神经网络，可反演得出实验楔体的参数。

2 遗传BP神经网络

BP神经网络是一种多层前馈神经网络，是目前应用最广泛的一种神经网络[8]。3层BP网络的拓扑如图4所示，包括输入层、一个隐含层和输出层。BP神经网络使用梯度下降算法调整权值和阈值。由于在调节权值过程中没有考虑前一时刻的梯度方向，学习过程会发生震荡，收敛缓慢。遗传算法(Genetic Alogorithm，GA)是一种全局优化搜索迭代算法。GA通过遗传算子模拟遗传过程中的选择、交叉、变异三个过程，对种群个体逐渐择优保留，最终获得最优个体，常应用于BP神经网络最优权值、阈值的搜索[9]。将GA和BP神经网路结合可以克服BP神经网络的缺陷，加快网络训练速度，以及提高网络的反演精度。

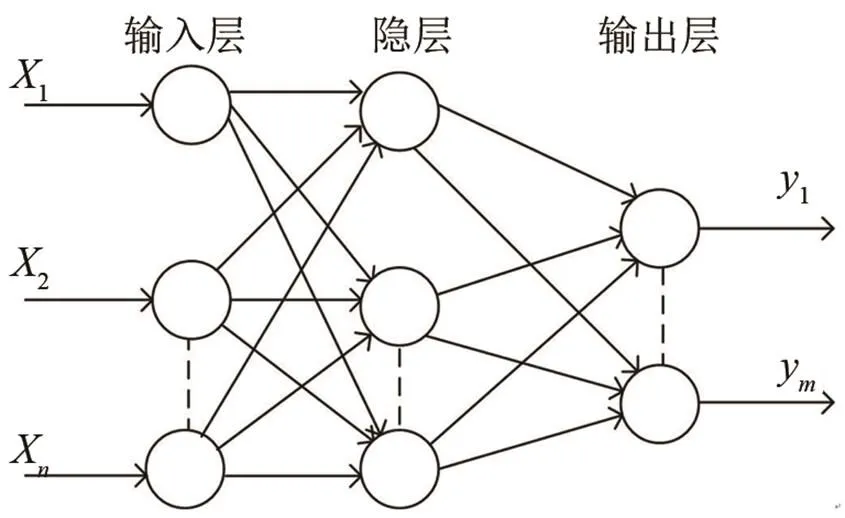
图4 3层BP神经网络

遗传算法优化BP神经网络的步骤如下：

(1) 建立BP网络，确定输入、输出神经元的个数，隐层数量，以及训练误差等。遗传算法编码权值、阈值，设定种群规模，种群初始化。

(2) 计算适应度函数，采用BP网络的绝对误差的倒数作为适应度函数。

(3) 进化过程，通过选择、交叉、变异三个操作，获得最优的个体。

重复步骤(2)~(3)，直到满足终止条件，获得最优个体的解码，作为BP神经网络的初始权值、初始阈值，算法流程如图5所示。

在进行训练前，需要对输入以及输出数据进行归一化处理，以防止数据超出隐层传递函数的值域限制。遗传算法需要合理设置种群数量以及进化的次数。种群数量小会降低算法的性能，种群数量太大，算法的效率会降低。这里选择种群数量为100，进化代数为200。交叉概率决定了种群中个体的更新速度，交叉概率太大，容易造成适应度高的个体被淘汰，交叉概率太小，容易降低搜索的速度。本次模型的交叉概率设为0.5，变异概率设为0.09。根据多次测试神经网络，隐层节点设为25比较合理，输入层和隐层之间、隐层和输出层之间的转移函数分别设为tansig型函数和pureline函数。设置BP神经网络的绝对误差为0.01。

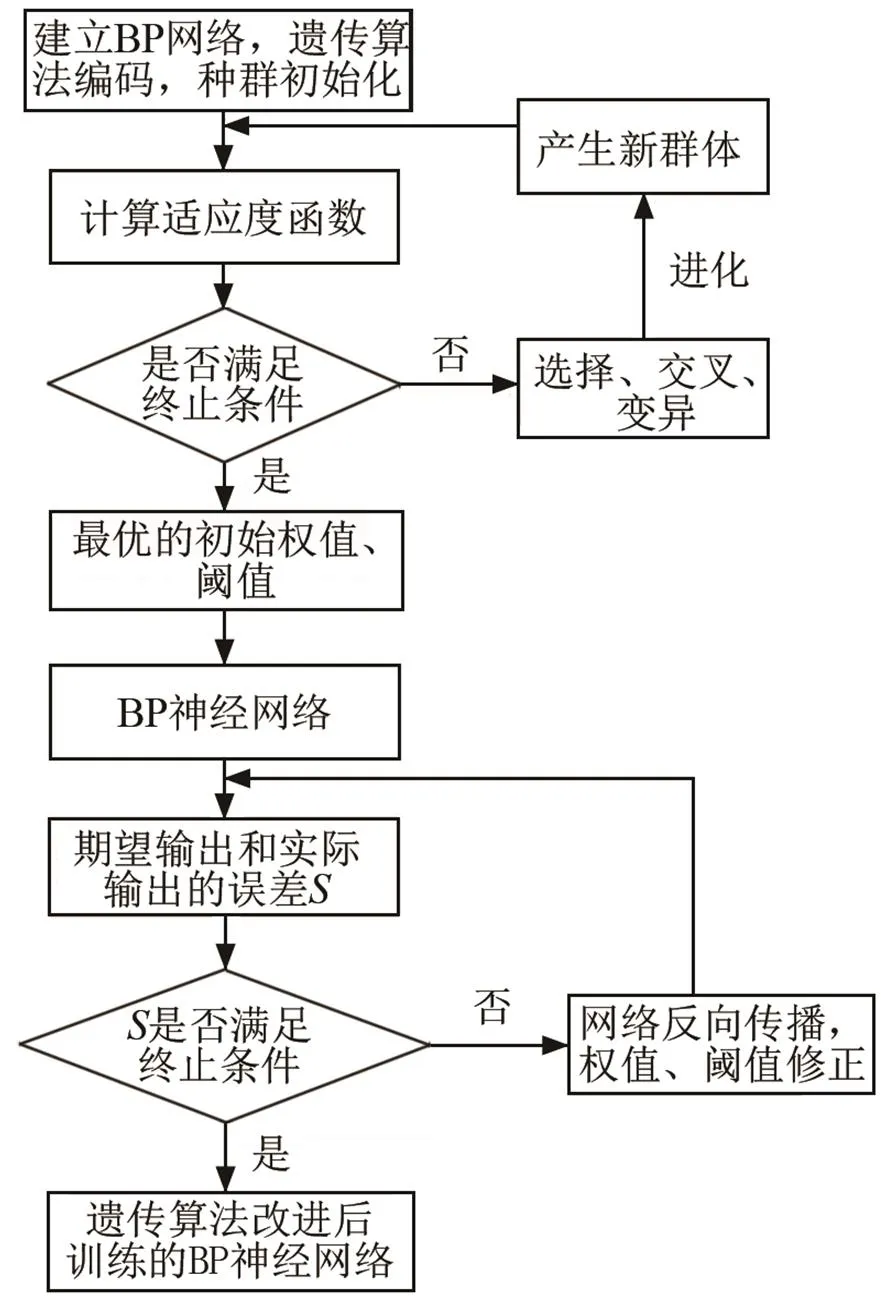
图5 遗传BP神经网络流程图

3 楔体参数反演

建立200组仿真模型，选取每一组模型频散数据A1模态在=1~6 MHz的数据点集合作为反演模型训练的输入数据，对应的参数集作为输出，进行网络训练。为了验证遗传BP神经网络反演模型的精度，选择10组数据对其进行性能测试。网络性能测试结果如图6所示。

测试样本反演得到的楔体的角度、密度、杨氏模量的相对误差分别在0~3%、1%~3%、2%~4%之间，参数反演精度较高。对实验室中的5组楔体分别进行参数反演，实验中采用基于光干涉法的光学检测实验装置对样品进行楔波检测[10]。实验装置如图7所示。

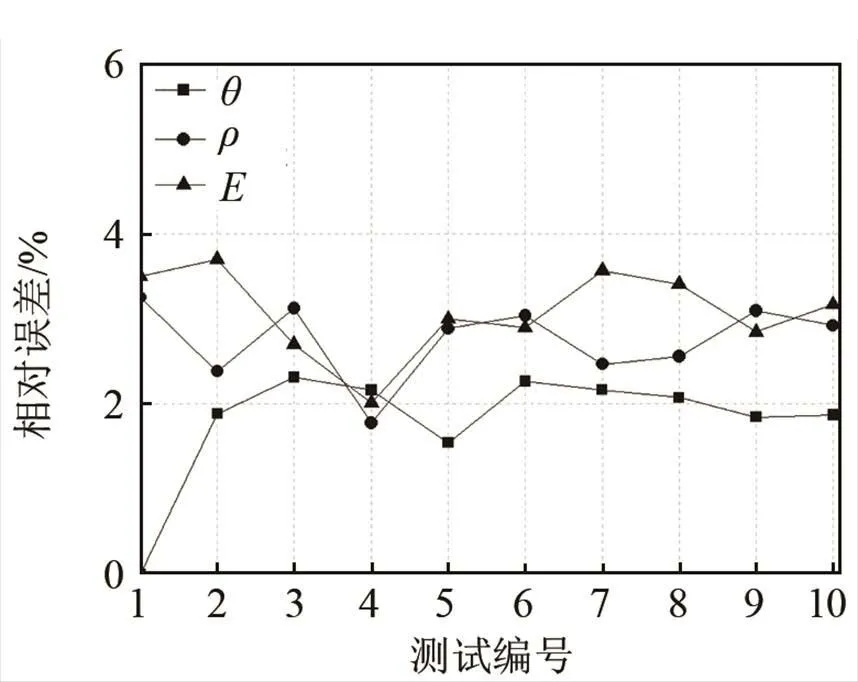
图6 遗传BP神经网络反演性能测试

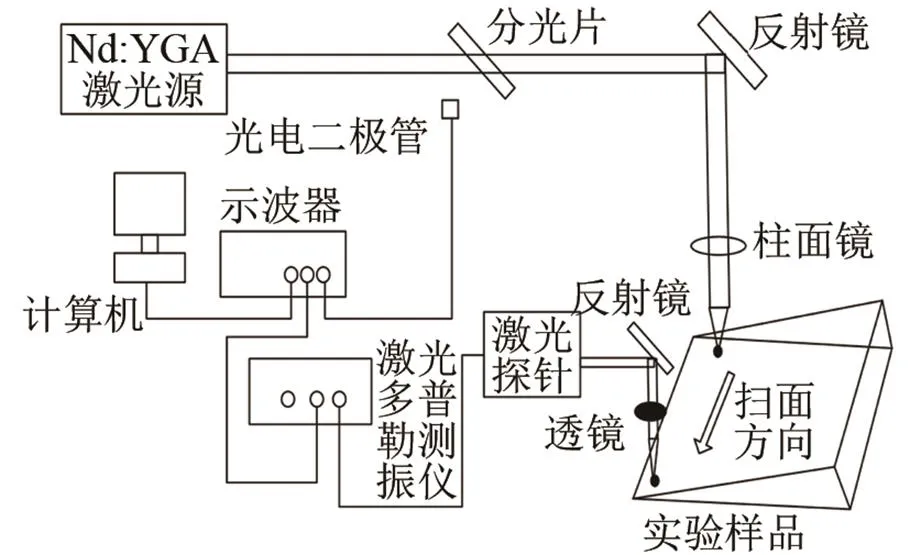
图7 楔波激发与接收实验示意图

激发部分采用Nd:YAG激光器，发射的波长为1 064 nm、脉宽7 ns、最大单脉冲能量为700 mJ的激光作为激发光源。辐照在楔体表面的激光能量被控制在热弹机制激发超声波的范围内，以避免材料表面损坏。脉冲激光通过分光片，部分反射光被光电二极管接收，传送到示波器作为触发信号。透射光由焦距为150 mm的柱面镜聚焦到样品表面。通过控制精密电控平移台，使激光线源沿楔尖方向移动扫查。探测光经过反射镜反射，焦距为150 mm的柱面镜聚焦到样品表面，通过感知样品表面反射的散射光的频移并转换为电信号输入示波器，实现声电转换，探测超声信号。图8为检测某一样品得到的位移-时间波形，对时域波形按照上述方法进行处理，可得到楔波的频散曲线，选取第一阶模态相速度代入训练好的反演模型，进行楔体楔尖角度、密度、弹性模量三个参数反演。

采用单一BP神经网络反演模型进行三个参数的反演，由表1可知反演的相对误差均较大，精度较低。

采用遗传BP神经网络反演模型进行参数反演，反演误差如图9~11所示。

由图9可知遗传BP神经网络和BP神经网络反演角度的相对误差分别在4%~10%之间，图10中两种模型反演密度的相对误差分别在5%~9%之间，图11中两种模型反演杨氏模量的相对误差分别在2%~7%。遗传BP神经网络反演三个参数的相对误差均小于BP神经网络，遗传BP神经网络的反演精度较之单一BP神经网络要高。楔体三个参数反演的相对误差较之图6测试遗传BP神经网络时的反演误差大，这是因为训练遗传BP神经网络反演模型的数据是通过仿真数据获得，在仿真条件下，反演模型建立的楔体参数和反对称第一阶模态相速度的关系非常精确，而实验数据和仿真数据之间存在着误差，导致实验样品反演的误差增大。

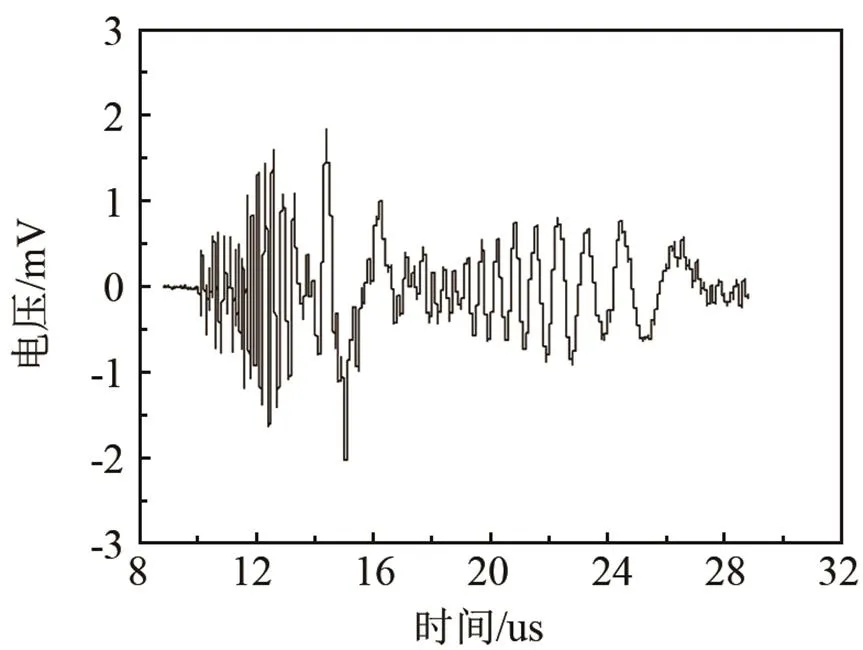
图8 楔波时域波形图

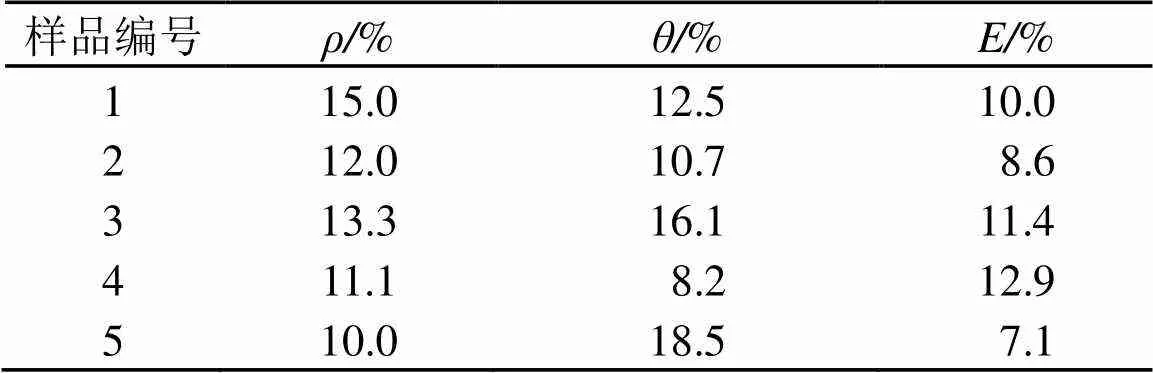
表1 BP神经网络反演楔体参数相对误差

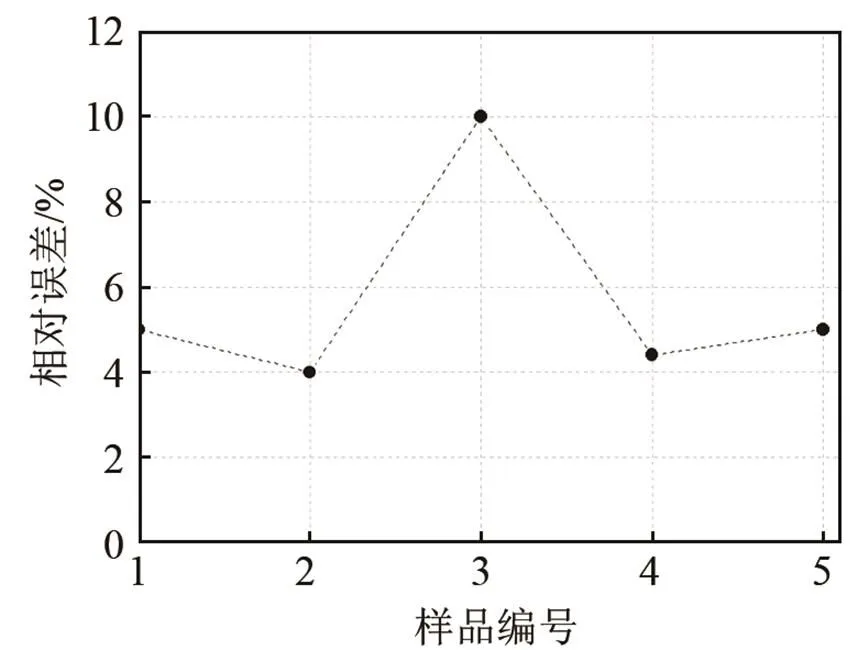
图9 遗传神经网络反演楔体角度相对误差

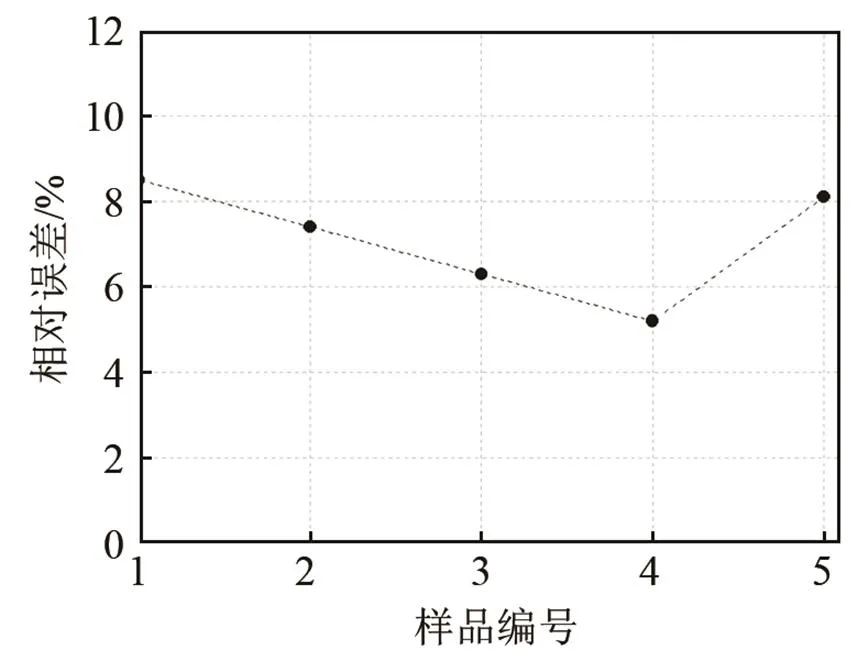
图10 遗传神经网络反演楔体密度相对误差

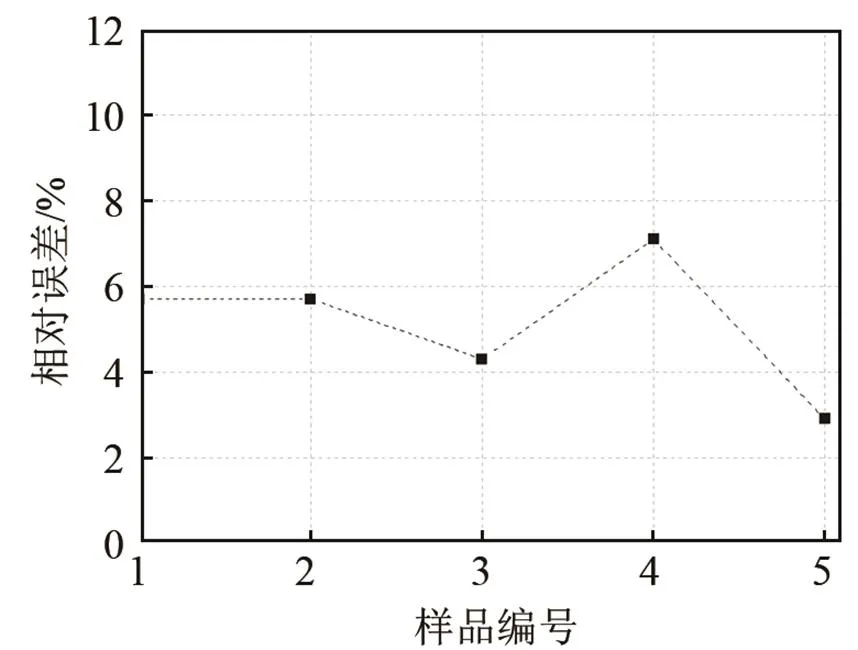
图11 遗传神经网络反演楔体杨氏模量相对误差

表2给出了两种模型下训练达到收敛所需的训练时间。

表2 两种模型训练时间

通过表2对比发现，在进行神经网络学习训练时，遗传BP神经网络达到收敛的所需时间远小于BP神经网络，网络收敛快，反演效率高。

4 结论

本文使用COMSOL软件仿真得到不同参数下对应的楔波频散数据, 将一阶模态相速度代入到遗传BP神经网络，训练遗传BP神经网络，得到楔体角度、密度、杨氏模量和反对称一阶模态相速度之间的关系，建立了楔体参数反演模型。采用基于光干涉法的光学检测实验装置对实验室中的楔体进行楔波检测。获得了实测楔体楔波频散数据，将实测数据代入反演模型，反演得到了样品楔体的角度、密度、样式模量三个参数，其相对误差均低于单一BP神经网络模型，反演精度较高。使用遗传BP神经网络反演楔体的参数，在实际应用是可行的，具有一定的工程价值。

[1] Lagasse P E, Mason I M, Ash E A. Acoustic surface waveguides - analysis and assessment[J]. IEEE Transactions on Sonics & Ultrasonics, 1973, 20(2): 143-153.

[2] Edwards R S, Dutton B, Clough a R et al. Enhancement of ultrasonic surface waves at wedge tips and angled defects[J]. Applied Physics Letters, 2011, 99(9): 094104-1-094104-3.

[3] 余凡, 赵英时, 李海涛. 基于遗传BP神经网络的主被动遥感协同反演土壤水分[J]. 红外与毫米微波, 2012, 31(3): 283-288. YU Fan, ZHAO Yingshi, LI Haitao. Soil moisture retrieval based on GA-BP neural networks algorithm[J]. Journal of Infrared and Milimeter Waves, 2012, 31(3): 283-288.

[4] 赵娟, 高正明. 基于BP神经网络的盲均衡器设计[J]. 声学技术, 2013, 32(3): 141-145. ZHAO Juan, GAO Zhengming. Design of a blind equalizer based on BP neural networks[J]. Technical Acoustics, 2013, 32(3): 141-145.

[5] Mckenna J, Boyd G D, Thurston R N. Plate theory solution for guided flexural acoustic waves along the tip of a wedge[J]. IEEE Transactions on Sonics & Ultrasonics, 1974, 21(3): 178-186.

[6] Krylov V V, Pritchard G V. Experimental confirmation of the propulsion of marine vessels employing guided flexural waves in attached elastic fins[J]. Journal of Fluids and Structures, 2007, 23(2): 297-307.

[7] Alleyne D, Cawley P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals[J]. J Acoust Soc Am, 1991, 89(3): 1159-1168.

[8] 李宏斌, 徐楚林, 温周斌. BP神经网络在扬声器异常音检测中的应用[J]. 声学技术, 2014, 33(6): 522-525. LI Hongbin, XU Chulin, WEN Zhoubin. The application of BP neural network in loudspeaker’s Rub & Buzz detection[J]. Technical Acoustics, 2014, 33(6): 522-525.

[9] 张学磊, 冯杰. 一种用于匹配场反演的遗传算法[J]. 声学技术, 2015, 34(5): 462-466. ZHANG Xuelei, FENG Jie. A new genetic algorithm for matched-field inversion[J]. Technical Acoustics, 2015, 34(5): 462- 466.

[10] JIA J, SHEN Z, SUN K. Study of the impact of truncations on wedge waves by using the laser ultrasound technique[J]. Applied Optics, 2015, 54(24): 7406-7412.

Research on genetic BP neural network based wedge parameter inversion

ZHANG Yu, JIA Jing, HAN Qing-bang, JIANG Xue-ping, SHAN Ming-lei, ZHU Chang-ping

(College of Interhet Of Things Engineering, Hohai Universitg, Changzhou 213022, Jiangsu, China)

In order to obtain the material parameters of an unknown wedge, an inversion model based on back propagation neural network combined with genetic algorithm is established. The wedge wave dispersion curves with different angles, density and young modulus are obtained by simulation. The phase velocity of the first mode in the anti-symmetrical flexural modes is chosen as the inputs of the established model. Genetic algorithm is introduced to get the optimized initial weight and threshold. Then the optimized results are taken to train the BP neural network.The first mode data measured from samples are used as the inputs of the network that has been trained to get the inversion results. It is found that the inversion model can be used to inverse angle, density and young modulus simultaneously. Compared with the single BP neural network, combining genetic algorithm has the advantages in fast convergence speed and high precision.

inversion; wedge waves; dispersion; BP neural network; genetic algorithm

TB551

A

1000-3630(2017)-01-0001-05

10.16300/j.cnki.1000-3630.2017.01.001

2016-05-04;

2016-07-18

国家自然科学基金(11574072, 11274091)、江苏省重点研发计划(BE2016056)、河海大学中央高校基金项目(2015B04714, 2015B04614)资助项目。

张雨(1991－), 男, 江苏徐州人, 硕士研究生, 研究方向为通信与超声技术。

韩庆邦, E-mail: hqb0092@163.com。