燕云水电站重力坝坝基渗透稳定影响分析

徐 彬，卢发周，李岩松

（1.南京市水利规划设计院股份有限公司，南京 210022；2.淮安市水利勘察设计研究院有限公司，江苏 淮安 213001）

燕云水电站重力坝坝基渗透稳定影响分析

徐 彬1，卢发周1，李岩松2

（1.南京市水利规划设计院股份有限公司，南京 210022；2.淮安市水利勘察设计研究院有限公司，江苏 淮安 213001）

以拟建燕云水电站重力坝为例，采用有限元法计算了坝基在水位下降过程中的应力应变特性，研究了在水位下降过程中坝基破坏模式、抗滑稳定系数、渗流场和坝基垂直有效应力分布等4个方面的变化趋势。结果表明：上游水位下降对该重力坝坝基破坏模式影响显著，上游水位较高时为表层滑动，死水位时为浅层滑动；水位下降还将导致重力坝抗滑稳定系数增大，坝基最大渗流速度和渗漏量也逐渐降低，坝基防渗墙底部最大垂直有效应力逐渐增大，坝趾垂直有效应力则逐渐减小，坝踵应力水平均较低，不存在受拉现象，满足规范要求。研究成果对工程建设的顺利开展有一定指导意义。

水电站；重力坝；有限元法；坝基渗流；稳定系数

1 工程概况

规划拟建燕云水电站位于四川省阿坝州松潘县燕云乡境内，属岷江河右岸一级支流开发的第一级，电站主要任务是防洪和发电。电站由首部枢纽、输水系统、厂区枢纽三大部分组成。水库总库容82万m3，属小（2）型水库，为碾压混凝土重力坝。大坝坝轴线长125m，最大坝高25m，坝顶宽4.5m，背坡1∶0.7，迎水面垂直。为了防止坝基渗流，设计了混凝土防渗墙，深入透水性较弱的新鲜基岩2m。

在大坝设计过程中，由于考虑了重力坝坝体上游不同水位工况下坝基底部岩体内的渗流作用，特别是进行地基承载力计算时需同时考虑孔隙水压力的影响，这给大坝设计过程中的稳定性验算带来困难。为此，本文提出采用有限元法为计算方法，从该重力坝坝体的破坏模式、抗滑稳定系数、渗流场分布和坝基垂直有效应力分布等4个方面分析上游不同特征水位时重力坝的应力应变特性，为该重力坝工程的设计和后期施工提供借鉴和参考。

2 渗流理论、模型构建及计算工况

2.1 渗流理论

根据达西（H.Darcy）［1-3］在垂直圆管中装砂进行的渗透试验，发现渗透量Q除了与断面面积A直接成正比外，其正比水头损失hw，反比于渗径长度L，渗透坡降J为hw与L的比值，引入决定土粒结构和流体性质的一个渗透系数k，则达西渗透定律为：

2.2 模型构建

计算选取该工程水电站重力坝最大设计断面进行建模分析，断面最大坝高25m，坝顶宽4.5m，背坡1∶0.7，迎水面垂直。为克服重力坝模型边界效应的影响，设置重力坝模型坝基长55m，高16m，模型包含3种岩体材料，表层为碎石土，中部为微透水泥岩层，底部为新鲜砂岩层。本文初始应力考虑自重应力，由于缺乏初始地应力资料，故暂不考虑岩层中的初始地应力。

先在CAD中建立好模型，再导入有限元软件PLAXIS.V.B中进行计算，岩体材料模型为修正摩尔—库伦模型，考虑了岩体间非线性特性，修正的摩尔—库伦弹塑性模型可以模拟应力增量随应变逐渐减小的硬化现象，更符合实际情况。

为保证计算结果准确可靠，对模型进行有限元网格划分时，将坝体与坝基及防渗墙附近岩体网格进行加密处理，模型含778个单元，7426个节点，如图1。

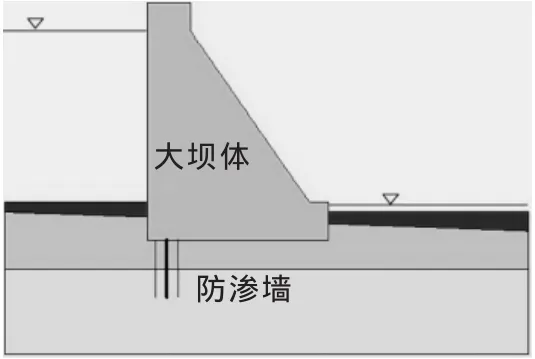
图1 重力坝模型

依据工程地质勘查岩芯取样及室内试验结果，得到重力坝模型各部分有限元计算力学参数。一般情况下岩石渗透系数很小，常规计算可以忽略不计。但由于本文主要研究对象是重力坝坝基的渗透稳定，因此需考虑坝基岩石的渗透作用。根据燕云电站现场钻孔的压水试验结果，可以获得重力坝坝基各岩层的吕荣值（q），吕荣值可定义为1MPa压力作用下1m试段内每分钟注入1L水量（L/min）。根据压水试验的吕荣值，换算得到坝基各岩层的渗透系数。由于本文研究对象为坝基，因此暂不考虑大坝坝体的渗透性。重力坝和坝基有限元计算力学参数如表1。

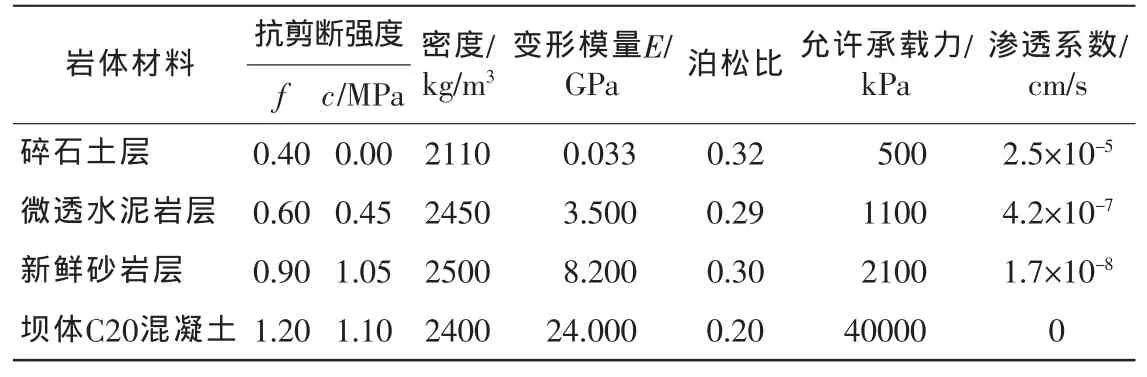
表1 重力坝和坝基有限元计算力学参数

重力坝坝基模型中设有防渗墙，位于坝踵下游1m，深度5m，单独采用PLAXIS软件中的板单元进行模拟，为弹塑性材料，且具有不透水性质，重力坝坝基中的防渗墙厚度1m。软件中板单元两侧设置界面单元，用于模拟防渗墙与岩体间的相互接触作用［4-7］。

2.3 计算工况

重力坝坝基稳定计算工况主要包括上游蓄水位从校核洪水位开始，下至设计洪水位、正常蓄水位和死水位等4种水位工况。4种不同工况上、下游水位设置如表2。

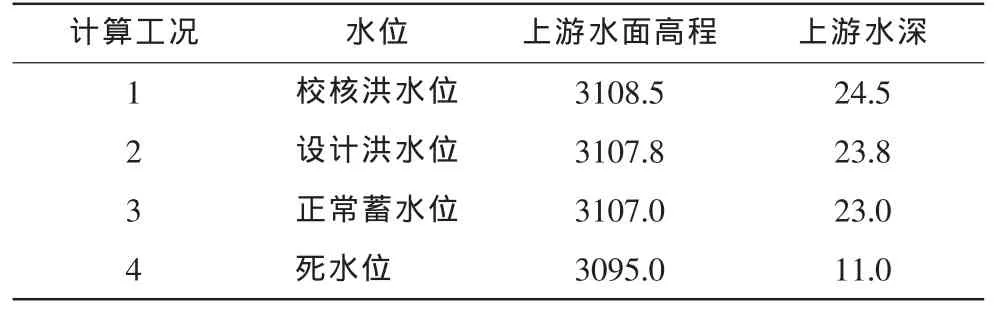
表2 各计算工况水位设置 单位：m

3 结果分析

3.1 破坏模式及稳定

随着重力坝上游水位的逐渐下降，静水压力和坝基扬压力随之减小，重力坝坝基抗滑稳定性也将随之改变。文中采用PLAXIS软件中自带的有限元强度折减法［11-13］（极限破坏板块）计算，得到了重力坝上游水位从校核洪水位降低至设计洪水位、正常蓄水位和死水位时坝基的破坏模式，结果如图2。

分析发现：①当校核洪水位、设计洪水位和正常蓄水位3种水位时，重力坝坝基的破坏模式基本相同，滑裂面为折线形，滑裂面起于上游坝踵以上5m处，终止于从下游坝基，剪切出口距离坝趾10m，且均属于表层滑动；②当水位降低至死水位时，滑裂面为圆弧形，圆弧起于上游坝踵以上2m处，中间与泥岩层和砂岩层分界线相切，从坝趾下游10m处剪出，此时的重力坝坝基破坏模式属于浅层滑动。

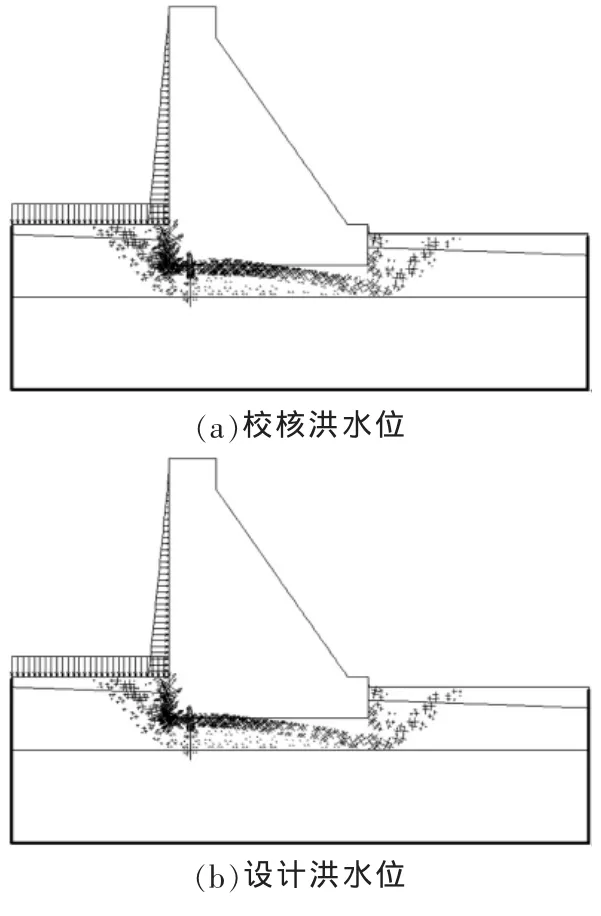
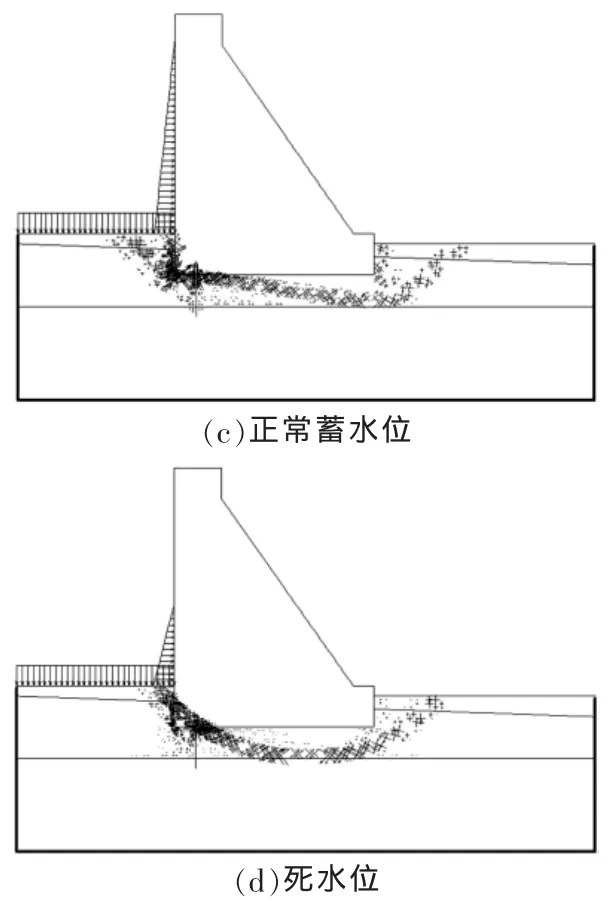
图2 坝基极限破坏模式

由于本工程地质上不存在软弱结构面时，故在计算过程中未发生深层滑动问题，与实际情况一致。

综上表明：上游水位下降对于重力坝坝基破坏模式存在显著影响，上游蓄水位较高时为表层滑动，上游蓄水位较低时为浅层滑动。为定量表述不同工况下重力坝坝基的稳定性大小，根据重力坝坝基极限破坏时有限元法稳定计算结果，得到了4种特征水位下重力坝的抗滑稳定系数，如图3。

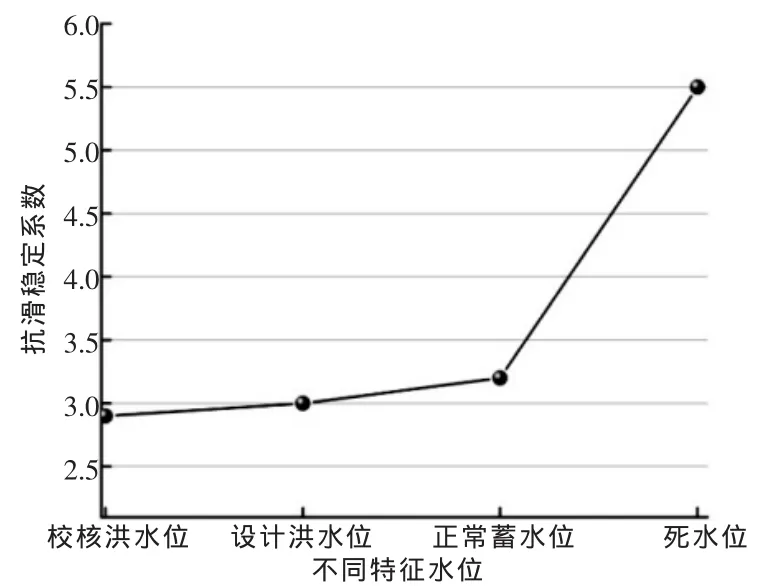
图3 抗滑稳定系数

分析可知，随着上游水位降低，重力坝抗滑稳定安全系数有增大的趋势，在校核洪水位时稳定系数为2.89，大于DL5018—1999《碾压混凝土重力坝设计规范》（下文简称规范）允许值［2.8］，水位降低至设计洪水位和正常蓄水位时安全系数分别为3.05和3.18，大于规范允许值 ［3.0］，而在死水位时安全系数为5.06。

造成以上结果，是随着重力坝上游蓄水水位的下降，坝体受水平向右的推力也同时减小，相应的扬压力和渗流力也相应减小，故重力坝坝基抗滑稳定性大大提高，抗滑稳定系数逐渐增大。

3.2 渗流

图4给出了水位下降过程中坝基渗流流速分布情况。从图4和图5可以看出，大坝坝趾位置的渗流流速最大，且水位的下降将导致最大渗流流速的减小，校核洪水位时最大渗流速度9.72×10-6m/d，设计洪水位时最大渗流速度9.55×10-6m/d，正常蓄水位时最大渗流速度9.39×10-6m/d，死水位时降至4.22×10-6m/d。说明随着重力坝上游蓄水位的降低，坝基最大渗流速度也逐渐降低。

进一步分析图5中的渗流路径，可以发现渗流轨迹线绕过防渗墙，渗径得到延长，有效的降低了坝趾附近的单宽渗流量，说明本次设计的防渗墙是合理的。

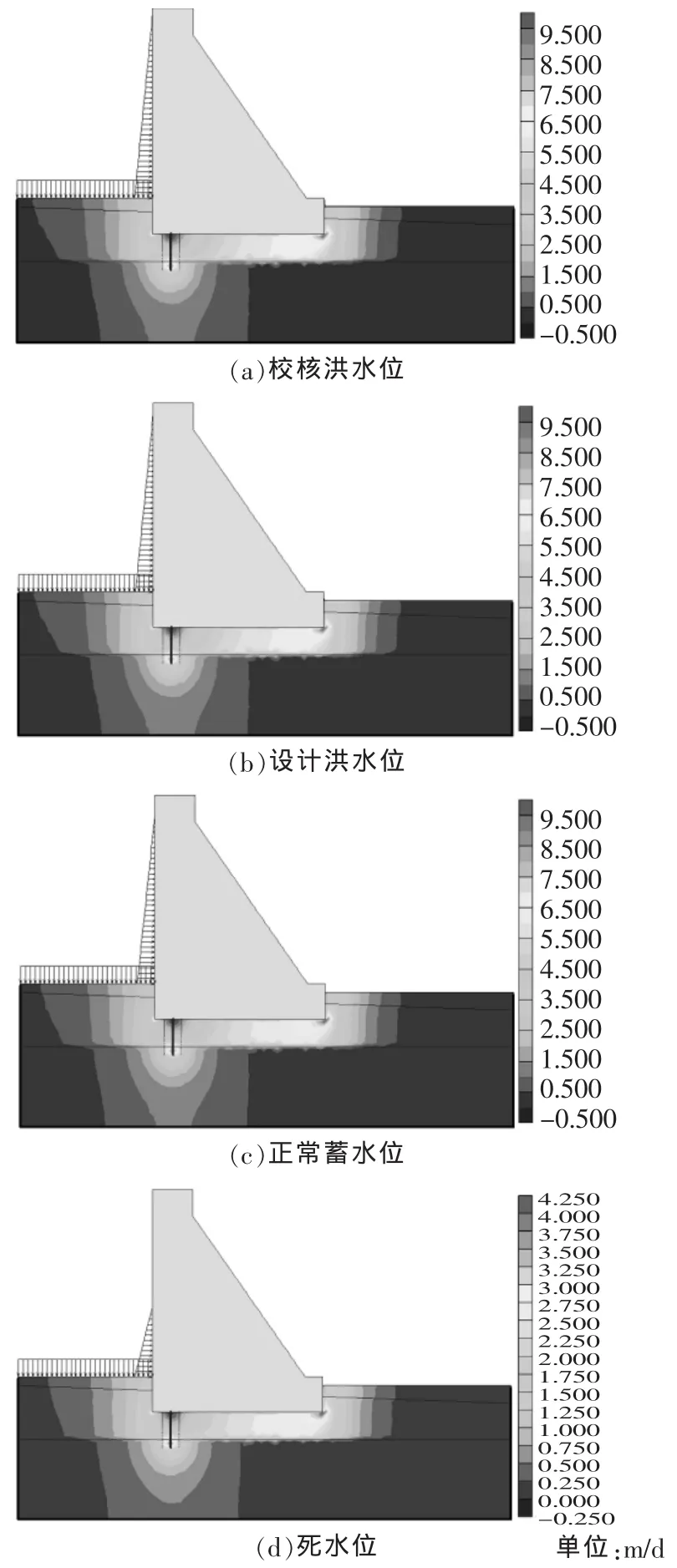
图4 不同特征水位坝基渗流流速

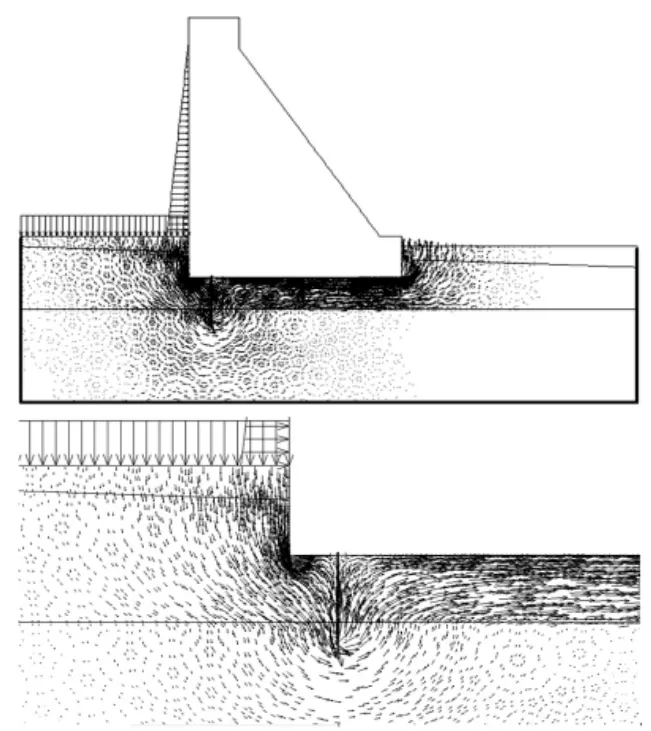
图5 正常蓄水位时坝基渗流矢量

3.3 应力

重力坝坝基应力计算主要计算各岩层的垂直应力，并与地基允许承载力进行比较。由于各工况均考虑了水压力作用的影响，地基岩土内存在孔隙水压力，故应力计算按照有效应力进行设置。本文规定有效应力中拉应力为正，压应力为负。

图6给出了4种特征水位下重力坝坝基的垂直有效应力分布情况，可知各工况时最大的垂直有效应力均分布在防渗墙底部一定范围内岩体上，说明设置的防渗墙可有效传递坝体的应力至新鲜砂岩层，从而降低了中部泥岩受力。

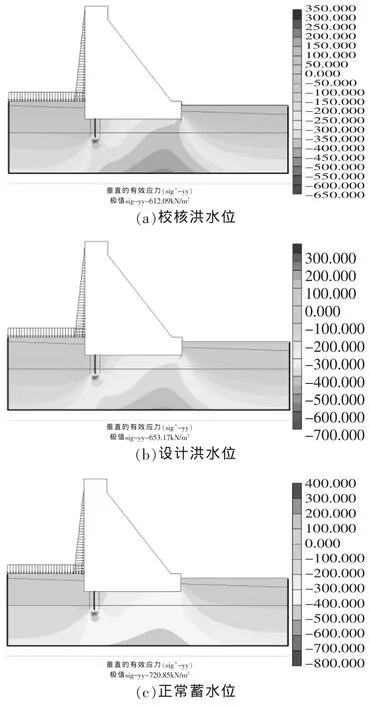
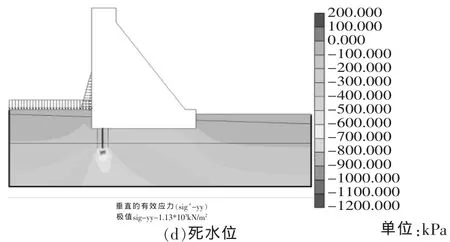
图6 不同特征水位坝基垂直有效应力

（1）在校核洪水位时，最大垂直有效应力612.09kPa，坝底部最大垂直有效应力位于坝趾，为450kPa，越往上游压应力越小。

（2）在设计洪水位时，最大垂直有效应力653.17kPa，坝底部最大垂直有效应力位于坝趾，为400kPa，越往上游压应力越小。

（3）在正常蓄水位时，坝基防渗墙底部最大垂直有效应力增大到720.85kPa，坝底部最大垂直有效应力区位于坝趾以上4m长的区域，为350kPa。

（4）当上游水位降低至死水位时，坝基防渗墙底部最大垂直有效应力增大到1.13MPa，远远大于以上3种工况，但小于砂岩的允许承载力2.1MPa，故设计满足地基承载力要求。

分析结果表明：随着上游蓄水位的逐渐降低，坝基防渗墙底部最大垂直有效应力逐渐增大，坝趾垂直有效应力则逐渐减小，坝踵应力水平均较低，但不存在受拉现象，满足规范要求。

4 结语

本文选取拟建燕云水电站重力坝为计算案例，研究了重力坝在上游蓄水位下降过程中坝基破坏模式、抗滑稳定系数、渗流场分布和坝基垂直有效应力分布等4个方面的变化趋势，得到以下结论：

（1）上游水位下降对于该重力坝坝基破坏模式影响显著，上游水位较高时为表层滑动，降低至死水位时为浅层滑动，水位下降将导致重力坝抗滑稳定系数增大。

（2）随着重力坝上游蓄水位的降低，坝基最大渗流速度和渗漏量也逐渐降低。渗流轨迹线绕过防渗帷幕，渗径得到延长，有效地降低了坝趾附近的单宽渗流量。

（3）随着上游蓄水位的逐渐降低，坝基防渗墙底部最大垂直有效应力逐渐增大，坝趾垂直有效应力则逐渐减小，坝踵应力水平均较低，但不存在受拉现象，满足规范要求。

（4）验证了燕云水电站重力坝在不同水位下的渗透稳定性均满足规范要求。

［1］毛昶熙.渗流计算分析与控制［M］.北京：中国水利水电出版社（第二版），2003.

［2］赵振兴，何建京.水力学［M］.北京：清华大学出版社，2010．

［3］DRUCKER D C，PRAGER W.Soil mechanics and plastic analysis in limit design［J］.Quarterly of Applied Mathematics，1952，10（2）：157－165.

［4］汪亚超，方国宝，陈小虎，等.混凝土重力坝抗滑稳定实时分析方法［J］.人民长江，2013，44（20）：37-41.

［5］卢坤林，朱大勇.武都水库坝基深层抗滑稳定性评价中BD角的合理取值［J］.水利水电科技进展，2012，32（3）：35-38.

［6］吴杰芳，张林让，陈震.混凝土重力坝深层抗震抗滑稳定分析研究［J］.长江科学院院报，2010，27（6）：58-61.

［7］田娟娟.基于有限元强度折减法的复杂地基重力坝抗滑稳定分析［J］.甘肃水利水电技术，2016，52（5）：26-30.

［8］王河，王志鹏，李永刚.基于有限元超载—折减综合法的重力坝深层抗滑稳定性分析［J］.水电能源科学，2016，34（2）：65-68.

［9］孙伟，庞俊蕊，苏龙，等.重力坝深层抗滑稳定强度折减弹塑性有限元法［J］.人民黄河，2014，36（1）：107-108.

［10］ZIENKIEWICS O C，HUMPHESON C，LEWIS R W.Associated and non-associated visco-plasticity and Plasticity in soil mechanics ［J］.Geotechnique，1975，25（4）：671-689.

［11］刘树林，强菲，聂守智.勉县地质灾害分布与影响因素的相关性分析［J］.水利与建筑工程学报，2017，15（1）：165-170.

［12］赵川，刘小容.碎石土压重对基坑边坡稳定性影响数值模拟［J］.水利科技与经济，2016，22（12）：57-59.

［13］宋丹青.水库蓄水对库岸边坡稳定性的影响［J］.水资源与水工程学报，2015，26（5）：192-196.

Influence research on foundation stability of a concrete gravity dam of water level drop of Yanyun Hydropower Station

XU Bin1，LU Fa-zhou1，LI Yan-song2
（1.Nanjing Water Conservancy Planning Design Institute Co，Ltd，Nanjing 210022，China；2.Huaian Water Survey and Design Institute co.，LTD，Huaian 213001，China）

In order to study the foundation stability influence of gravity dam when upstream water level dropped，taking the Yanyun hydropower station dam as an example，the stress and strain characteristics of dam foundation in the process of water level decline is calculated by finite element method，we research four aspects of change trends during the water level decline：dam failure mode，the anti sliding stability，seepage field and the stress distribution of dam foundation vertical effective stress.The results show that the upstream water level decreased has significant influence on the dam foundation failure mode，the surface is sliding when the upstream water level higher，the shallow is sliding when at the dead water level；water level decline will lead to increase the anti sliding stability coefficient of gravity dam，dam foundation seepage and leakage rate is gradually reduced，the maximum vertical effective stress gradually increase at the bottom of the dam foundation impervious wall，the dam toe vertical effective stress decreases，the dam heel stress level was low，but there is no tension phenomenon，can meet the requirements of specification.The research results have certain guiding significance for the smooth development of engineering construction.

hydropower station；gravity dam；finite element method；seepage；stability factor

TV642.3

B

1672-9900（2017）05-0088-05

2017-07-27

徐 彬（1981-），男（汉族），江苏靖江人，工程师，主要从事水利工程项目管理工作，（Tel）18662707149。

（责任编辑：王艳肖）