高青县河网断面优化对调蓄能力的影响
2017-10-26余泽旻徐玉良
余泽旻,贾 超,徐玉良
(山东大学 土建与水利学院,济南250061)
高青县河网断面优化对调蓄能力的影响
余泽旻,贾 超,徐玉良
(山东大学 土建与水利学院,济南250061)
为研究河网断面优化对调蓄能力的影响,选取山东省淄博市高青县典型水环境区域,建立以纳维—斯托克斯方程和圣维南方程为基础的河网水动力模型,模拟高青县现有河网遭遇20年一遇洪水,研究区内河道水位响应情况,部分河段过水能力不足,洪水溢出,针对这些河段进行断面优化,再次模拟优化后的河网在洪水条件下的水位响应情况,基本满足行洪能力。研究结果表明,断面优化能够有效地改善河网调蓄能力,并针对区域洪涝防治工作提出有效防控措施,为提升城市防洪能力和生态功能提供有价值的科学技术支持。
高青县;河网;断面优化;调蓄;数值模拟
伴随社会经济快速发展,对水资源依赖度前所未有的紧密,水资源短缺、洪涝灾害等水问题严重威胁人民生产生活安全。同时自然环境受到人类活动的影响,城镇化进程加速,导致河流数量与面积持续减少,河网水系大幅萎缩,连通性阻断,调蓄能力减弱,河网结构简单化,此引发的洪涝灾害、水质恶化等问题 也日趋严重[1]。袁雯等[2]基于 数理统计的 方法,探讨了水面数量和河流结构等指标参数对河网调蓄能力的可能影响,并提出估算河网调蓄能力的方法。程江等[3]研究发现,水系衰减导致上海地区河道槽蓄容量较百年前减少80%,城市河网调蓄能力明显削弱。王柳艳等[4]研究表明,水系衰减对河网蓄泄功能产生较大影响,使得河网年平均水位和汛期水位均呈现上升趋势,洪涝风险增大。Zhang等[5]探讨了河网水系复杂程度与城市洪水频次的关系。王跃峰等[6-9]基于REW(Representative Elementary Watershed)概念与水位Hurst指数值,构建河网结构参数与调蓄能力的关系式,揭示了水系变化对河网调蓄能力的影响。然而,这些方法大多基于实际监测数据,选取水文指标参数,采用数值计算的方法对河网的调蓄能力进行分析研究,对于洪水期间河网水位实时响应情况的研究尚有不足。
鉴此,本文以山东省淄博市高青县典型水环境区域为例,建立以纳维—斯托克斯方程和圣维南方程为基础的河网水动力模型,采用数值模拟的方法,模拟研究区遭遇20年一遇洪水时,河道水位的响应情况,并针对行洪过流能力不足的河段进行断面优化,研究断面优化对调蓄能力的影响,为水网的规划与重建,调整水系结构,具有一定的指导意义。
1 理论及技术方法
选取山东省烟台市高青县典型水环境区域,建立以纳维—斯托克斯方程和圣维南方程为基础的河网水动力模型,反演在保证居民基本用水要求时,引黄闸引流的基础水流量,以及在高青县现有河网的基础上,预测遭遇20年一遇洪水时,研究区内河道水位响应情况,并对区域洪涝防治工作提出有效防控措施,为研究区开发建设过程中的水安全保护提供科学技术支持。
采用纳维—斯托克斯方程 (Navier-Stokes equation)描述黏性不可压缩流体动量守恒的运动方程。假设流体连续,不包含形成内部空间的空隙,如溶解气体的气泡等。假设用到的全部物理场如压强、速度、密度及温度等可微分。

采用一维圣维南方程组求解河网水动力模型。以Abbott六点中心隐式差分方法对圣维南方程进行数值离散,应用“追赶法”求解差分方程。计算过程中在每个网格点非同时计算水位、流量值,而是按照顺序交替进行计算。每个实测断面位置为水位计算点,两个水位计算点中点处为流量计算点。

式中 x为距离坐标;t为时间;A为过水断面面积;Q为流量;h为水位;q为旁侧入流量;c为谢才系数;R为水力半径;g为重力加速度;为动量修正系数。
采用小流域设计暴雨推理公式计算水网的设计洪峰流量。

式中 Qp为设计洪峰流量;Sp为设计频率暴雨雨力;为流域汇流时间;n为暴雨递减系数;F为流域面积;为洪峰流量径流系数。
2 工程分析
2.1 研究区概况及模型建立
研究区位于山东省淄博市高青县,地处黄河下游冲积平原,地形较为平坦,总地势西北高、东南低,自然比降1/7500,受半湿润半干旱大陆季风气候影响,研究区内降水年际变化较大,多年平均降水量563.6mm,平均蒸发量1628.5mm,降雨与蒸发年内分配不匀。相对湿度63%。多年平均气温12.4℃。研究区内水系较为丰实,黄河与小清河是高青县主要客水资源,支脉河、北支新河贯穿境内腹地,4条大中型河道及众多支流、干二排、干四排、杜姚沟等主排水沟要沟渠构成高青县的灌排网络。
为解决研究区水网存在的湖、河、沟、渠、湿地相互间未形成完善的体系、水资源开发利用程度不足,河网调蓄能力欠佳等诸多问题,以研究区主要大中型河道及沟渠为骨架,建立研究区河网计算模型,如图1。
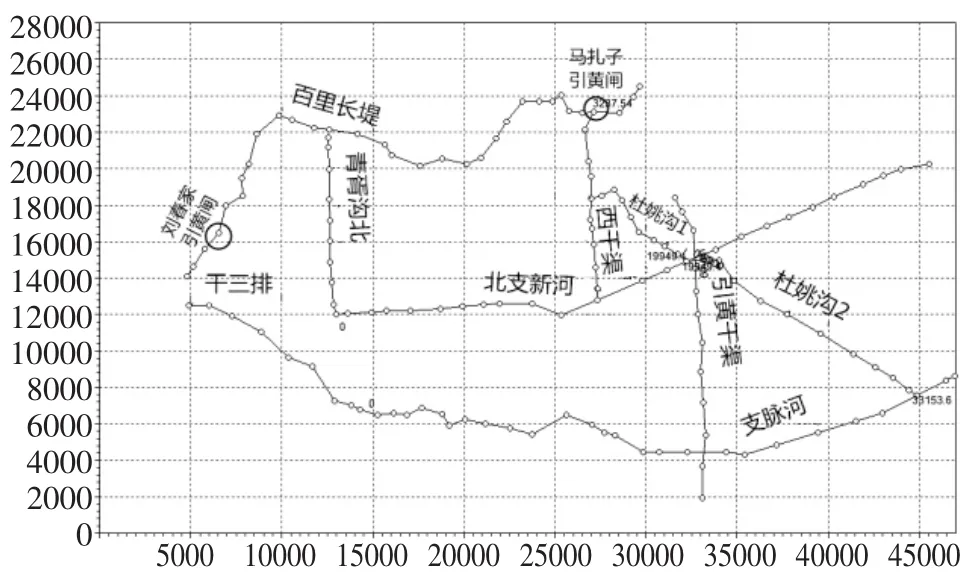
图1 研究区河网模型
2.2 相关参数
根据河道现状、规划要求及现有设计资料,每隔一定距离取一河道断面,作为计算节点,各河道断面参数如表1。
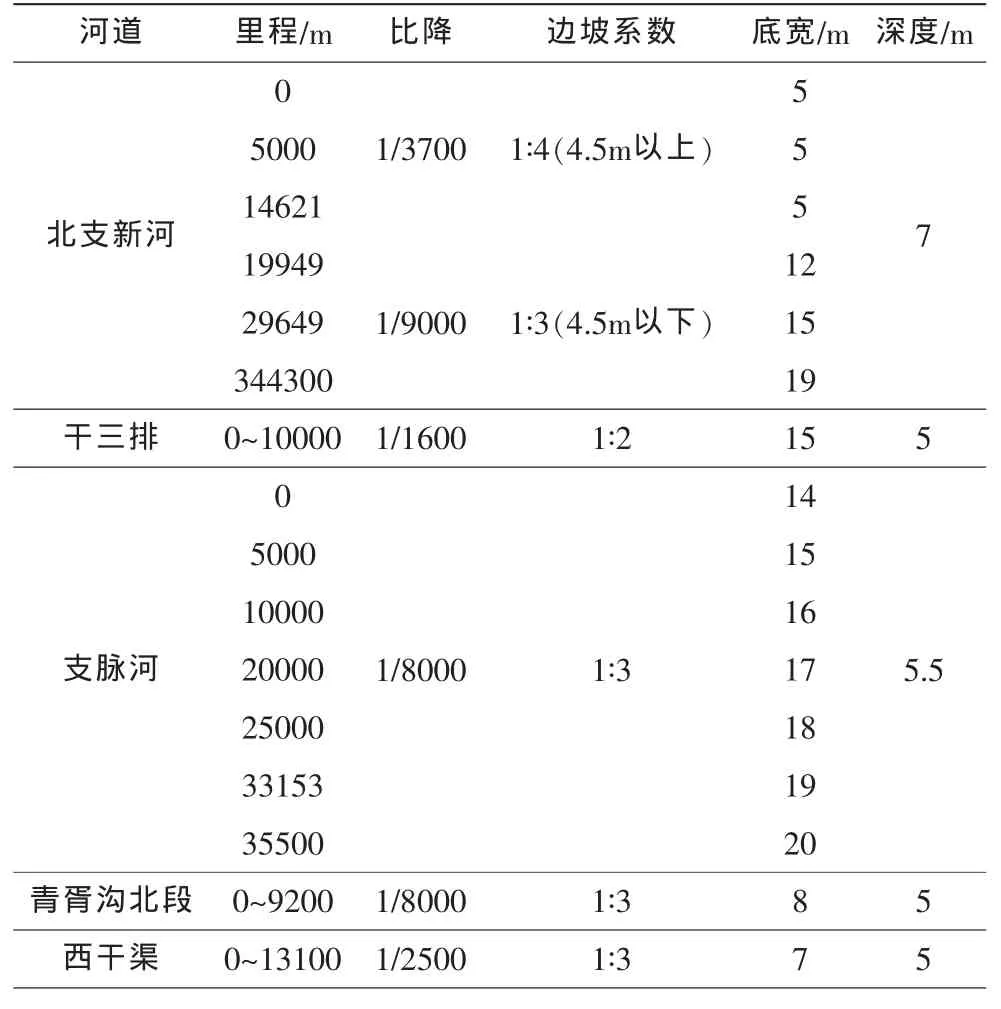
表1 各河道断面参数
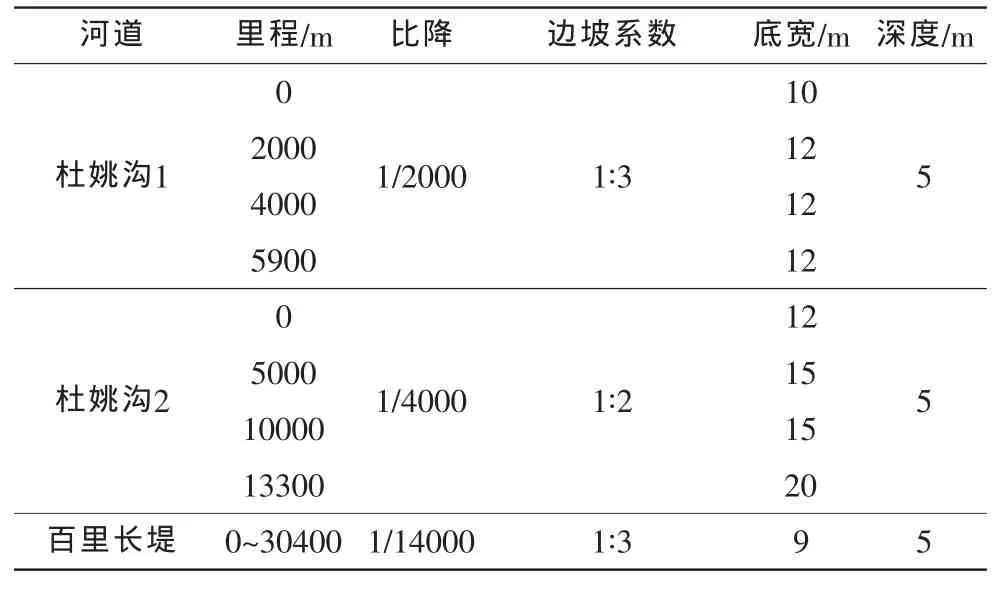
续表1
2.3 数值模拟及结果
为满足水网生态、景观等指标要求,各河道需达到一定水量及水深,同时,为保障水质,水体需达到一定的流动性,能满足此要求的最小流量,即河道基本流量。取河道糙率n为0.033,考虑各河道的汇流和连接关系,则刘春家引黄闸设计引水流量为37.5m3/s,马扎子引黄闸设计引水流量27.8m3/s,以及各河道基本流量如表2。
对河网进行20年一遇洪水(频率P=5%)防洪校核,检验各河道断面的过水能力。采用小流域推理公式,计算水网中各河道的洪峰流量,如表2。

表2 河道流量 单位:m3/s
当河道内流量分别为基本流量和洪峰流量时,河道内水位如图2~图8,纵坐标为标高,横坐标为距河段入口沿程距离(m)。

图2 支脉河沿程水位
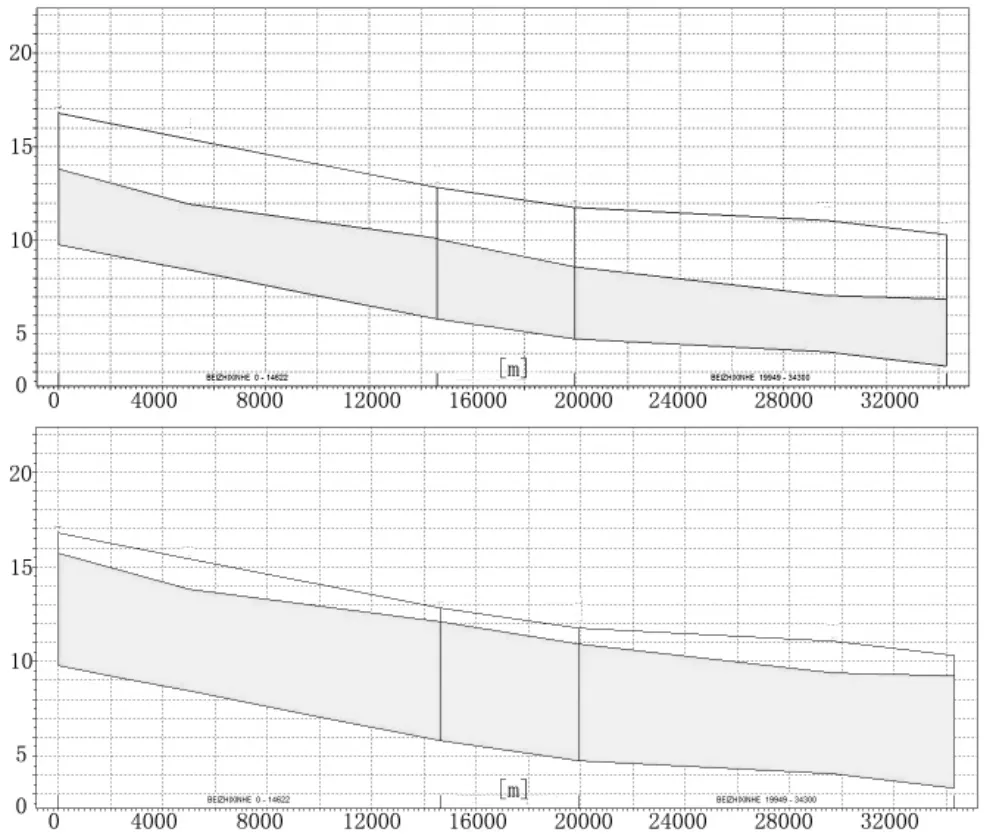
图3 北支新河沿程水位
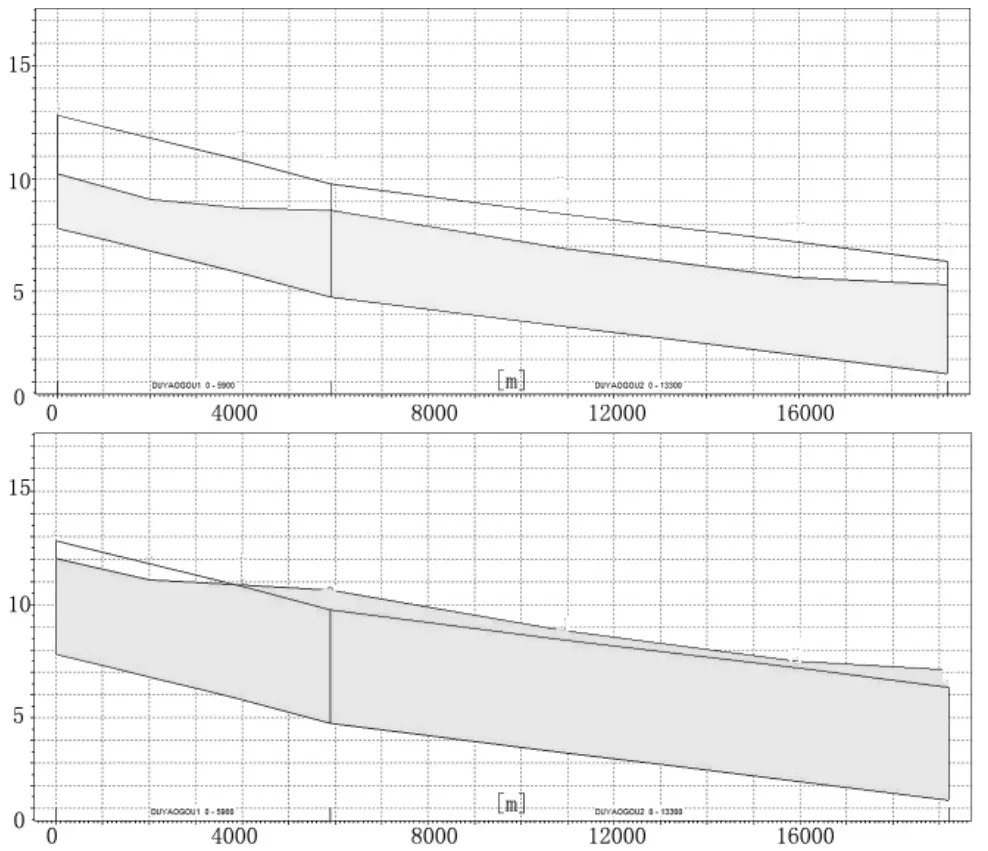
图5 杜姚沟沿程水位
由数值模拟结果可知,支脉河进口水位高出河堤0.4m,出口水位高出河堤0.67m;杜姚沟与北支新河交汇处水位高出河堤0.85m,出口处水位高出河堤0.75m;西干渠—东环河出口处水位高出河堤1.17m;青胥沟北段出口处水位高出河堤0.72m。洪水溢出河堤,需对该河段断面进行优化,其余河道断面过水能力满足条件,不需再次优化。
以河道实际情况为依据,采用“居民优先”的优化原则,进行断面优化。部分河段居民区距离河道较近,采用扩宽河面的方法则涉及土地征用,居民搬迁等实际问题,较为复杂难以处理,为适应工程实际,采用加深河道的方式;对于部分居民区距离河道较远,或不涉及此方面问题的河段,则采用扩宽河面的方式,以减少工程量,更为经济实用。优化后各河道断面参数如表3。
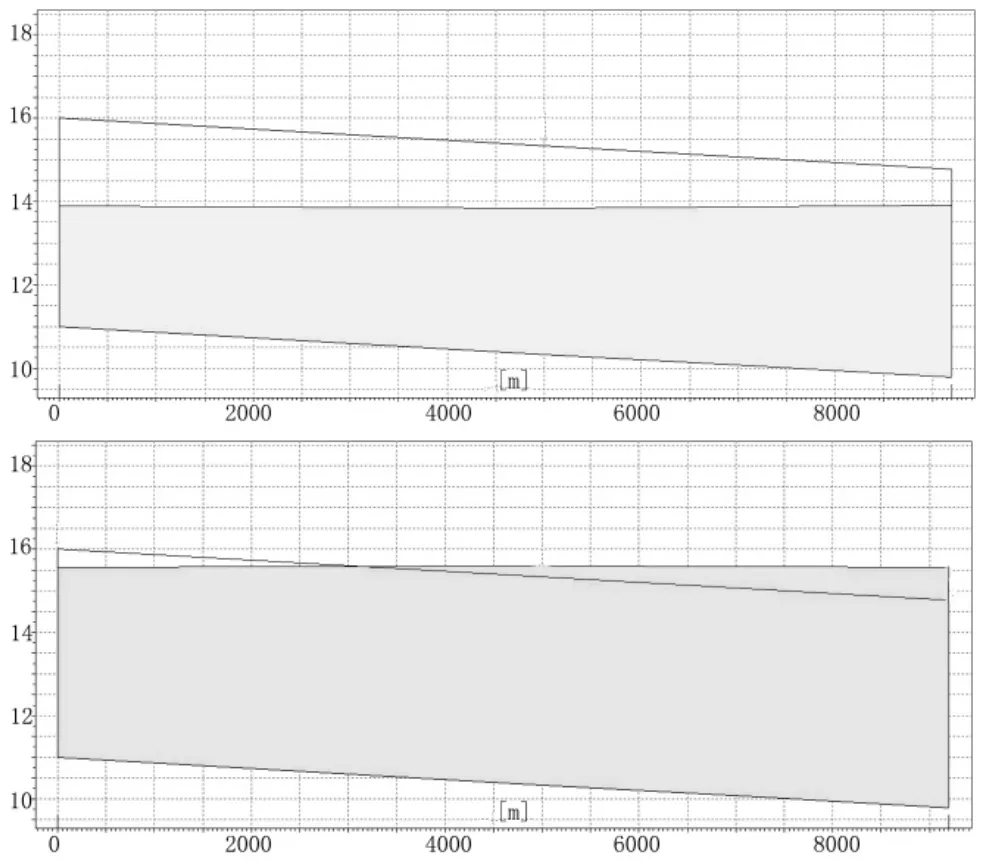
图6 青胥沟北段沿程水位

图7 西干渠沿程水位
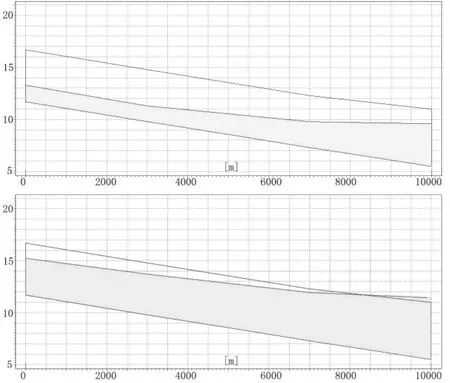
图8 干三排沿程水位

表3 优化后河道断面参数
在洪水条件下,对重新断面优化后的水网进行过水能力计算,如图9~图13。

图9 支脉河沿程水位

图10 杜姚沟沿程水位

图11 青胥沟北段沿程水位

图12 西干渠沿程水位
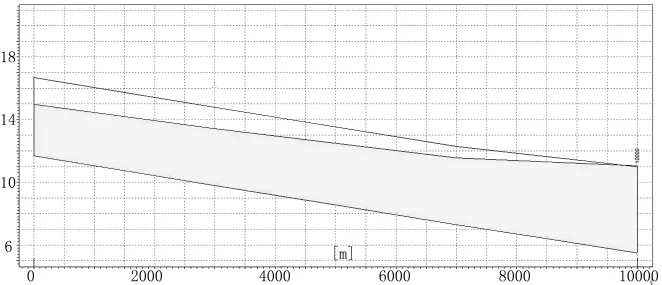
图13 干三排沿程水位
根据模拟结果,对不满足行洪的断面进行优化后,河道的过水能力显著提高,基本满足行洪要求,仅青胥沟北段出口处水位高出河堤0.1m,干三排出口处水位高出河堤0.1m,极小部分河道出口水位略微高于河堤高度,稍有溢出,综合考虑次级水网对洪水的缓解作用,不会造成洪水灾害,并且若再次进行断面优化,增加工程量且无较大实用价值,不够经济,故不再进行下一步断面优化。模拟结果表明,断面优化有效地提高了高青县水网的调蓄能力。
3 防控建议
3.1 断面优化
针对部分在遭遇强降雨时过流能力不足的河段,对该河段进行河面扩宽或河底加深等处理,提高河段过流能力。
3.2 清砂清淤
由于高青县水网中水多源自于黄河引水,黄河水中携带有大量泥沙,在高清水网中淤积,削弱河道过流能力,针对此现象,可定期对河道进行清淤,以维系其过流能力。
3.3 充分利用次级河道的缓冲作用
研究区水网体系中,除主要河道之外还有大量村民自行挖掘用以灌溉的沟渠及防洪排涝沟渠等,分布密集,形式复杂,可以充分利用次级河道,达到缓解洪水的作用。
3.4 开闸泄洪、建立排涝泵站
发生洪涝灾害时,可调节高青县水网的下节泄洪闸,开闸泄洪,起到洪水调节的作用,或建立排涝泵站,加速汛期洪水的排出。
4 结语
(1)以高青河网为例,采用数值模拟的方法对河网遭遇20年一遇洪水时,河道水位的响应过程进行模拟研究,发现支脉河、杜姚沟等部分河段水位高出河堤0.4~1.17m,河道过水能力不足,溢流严重。
(2)针对河段进行断面优化,再次模拟后仅青胥沟北段出口处,干三排出口处水位高出河堤0.1m,稍有溢出,综合考虑次级水网对洪水的缓解作用,不会造成洪水灾害。
(3)断面优化能够有效地改善河网调蓄能力,为水网的规划与重建,调整水系结构,提升城市防洪能力和生态功能提供科学技术支持。
[1]Cui B,Wang C,Tao W,et al.River channel network design for drought and flood control:A case study of Xiaoqinghe River basin,Jinan city,China[J].Journal of Environmental Management,2009,90(11):3675-3686.
[2]袁雯,杨凯,唐敏,等.平原河网地区河流结构特征及其对调蓄能力的影响[J].地理研究,2005,24(5):717-723.
[3]程江,杨凯,赵军,等.上海中心城区河流水系百年变化及影响因素分析[J].地理科学,2007,27(1):85-91.
[4]王柳艳,许有鹏,余铭婧.城镇化对太湖平原河网的影响:以太湖流域武澄锡虞区为例[J].长江流域资源与环境,2012,21(2):151-156.
[5]Zhang S,Guo Y,Wang Z.Correlation between flood frequency and geomorphologic complexity of rivers network:A case study of Hangzhou China [J].Journal of Hydrology,2015,527:113-118.
[6]Reggiani P,Sivapalan M,Hassanizadeh S M.A unifying framework for watershed thermodynamics:Balance equations for mass,momentum,energy and entropy,and the second law of thermodynamics[J].Advances in Water Resources,1998,22(4):367-398.
[7]Zhang G P,Savenije H H.Rainfall-runoff modeling in a catchmentwith a complex groundwater flow system:Applicationof the Representative ElementaryWatershed(REW)approach[J].Hydrology and Earth System Sciences,2005,9(3):243-261.
[8]马宗伟,许有鹏,钟善锦.水系分形特征对流域径流特性的影响:以赣江中上游流域为例[J].长江流域资源与环境,2009,18(2):163-169.
[9]王跃峰,许有鹏,张倩玉,等.太湖平原区河网结构变化对调蓄能力的影响[J].地理科学,2007,27(1):85-91.
The influence of river-network cross-section optimization on storage capacity in Gaoqing
YU Ze-min,JIA Chao,XU Yu-liang
(School of Civil Engineering,Shandong University,Jinan 250061,China)
To study the influence of the river cross-section optimization on storage capacity,based on navier-stokes equations and Saint Venant equations,this paper built the hydrodynamic model and modeled the water level response when river network in Gaoqing suffered 5%frequency flood.Part of the river water capacity were insufficient,and the flood overflow.According to this phenomenon,we optimized river section and simulated again,and then met the flood discharge capacity basicly.The results show that the cross-section optimization can effectively improve the river network storage capacity.Effective prevention and control measures are put forward based on regional flood control work.This paper improves the capacity of city flood control and ecological function and provides the valuable support of science and technology.
Gaoqing county;river-network;cross-section optimization;storage capacity;numerical modeling
TV212.5
B
1672-9900(2017)05-0015-06
2017-07-04
余泽旻(1992-),女(汉族),湖北随州人,硕士研究生,主要从事水利工程方面的研究工作,(Tel)18753160822。
(责任编辑:尹健婷)
