泵站钟形进水流道吸水室后壁形状的研究

叶鹏　刘超　许健　查智力　黄佳卫

摘要：基于三维不可压缩流体的雷诺平均N-S方程和RNGk-ε紊流模型，对矩形、半圆形和“ω”吸水室后壁形状的钟形进水流道泵装置进行了三维紊流数值模拟，并分析了钟形进水流道后壁形状对泵装置水力特性的影响。相同流量下，“ω”形吸水室进水流道流线分布最规则，漩涡比其他形状的进水流道小，“ω”形吸水室进水流道水力损失比矩形吸水室进水流道小1cm；出口断面的流速均匀度达到93%，比矩形和半圆形吸水室进水流道高约2个百分点；出口断面速度加权平均角度达到83.5°，比矩形吸水室进水流道高0.6°，比半圆形吸水室进水流道高0.2°；泵装置运行高效区流量范围比半圆形的拓宽了7.3%，比矩形的拓宽了30%。该研究对于完善泵站钟型进水流道吸水室优化设计具有一定意义。

关键词：泵装置；钟形进水流道；后壁形状；数值模拟；优化设计

中图分类号：TV131.4 文献标识码：A 文章编号：1672-1683（2017）05-0195-07

进水流道是泵站前池和水泵的叶轮室之间的过渡段，是整个泵装置的重要组成部分。进水流道的主要作用是使水流加速和更好地转向，为叶轮室进口提供良好的水力条件。故其出口流态对水泵的能量性能、汽蚀性和安全性能有很大影响。

钟形进水流道是一种比较好的进水流道形式。它的显著特点是高度较小，流道宽度较大，可以减少泵站基础的挖深，从而降低土建工程投资。这对于某些站址地质较差的泵站，具有特别重要的意义。钟形进水流道的几何形状比肘形进水流道更为复杂，因此设计难度更高，而且现在也没有成熟的水力设计方法。钟形进水流道的后壁形状常见的有“ω”形，圆弧形，多边形和矩形，一般多采用前两者[5]。

近年来，我国在钟形进水流道数值模拟与实验方面的研究越来越广泛。在优化钟形进水流道吸水室后壁形状方面，国内已有不少学者做了研究。刘超等在泵站节能技术改造中，将后壁形状为“ω”形的钟形进水流道用于圬工泵站，优化了进水流态，现场测试结果表明提高了泵装置运行效率。颜红勤等对不同钟形进水流道的优化方案进行了实验和数值模拟，认为“ω”形后壁吸水室钟形进水流道的水力性能良好，水力损失小。陶海坤等模拟计算了两种不同“ω”形后壁吸水室钟形进水流道，认为采用公式V_u=const来设计“ω”形吸水室较好，并且还研究了吸水室的后壁距。

上述研究主要是只针对钟形进水流道进行数值模拟分析，不包括水泵，因此不能反映进水流道对水泵性能的影响。本文结合其他相关研究，通过CFX对包括水泵在内的三种方案的泵装置进行全模拟，着重分析钟形进水流道不同截面的流线和速度分布、内部流态、水力损失以及其对泵装置性能的影响，为泵装置眭能优化提供依据。

1计算模型和网格

1.1几何建模

本次研究的进水流道后壁形状有矩形（方案1），圆弧形（方案2），“ω”形（方案3），其中“ω”形的后壁形状是平滑过渡的曲线形状，由两个大小圆弧组成，大圆弧的圆心与泵轴线重合，小圆弧圆心O₂在喇叭口圆周后侧垂直于流向的切线上。钟形进水流道各主要几何参数见图1。本文采用轴流泵型号为ZM6。

本文研究的泵装置模型主要由钟形进水流道、叶轮、导叶及虹吸式出水流道组成，其中叶轮、导叶模型在Turbogrid软件中建立，进、出水流道在UG软件中建立。泵装置的三维模型见图2。

1.2网格划分

由于该泵装置形式比较复杂且不规则区域较多，为了提高计算的精度，本文采用结构化网格。进、出水流道采用ANSYS mesh软件剖分，叶轮及导叶网格采用Tuobogrid软件中H/J/L-Grid拓扑结构剖分。本文不断调整网格数量并对不同网格数量的泵装置效率进行计算，发现当网格增加到一定数量时，计算结果不再随着网格数量的增加而改变。在满足网格无关性要求时，取方案1泵装置网格总数2 556 027（方案2为2 548 004，方案3为2 520 150），其中叶轮网格数456 192，导叶网格数1012 662，进水流道网格数349 190（方案2为341 167，方案3為313 3 13），出水流道网格数为737 983。网格划分见图3。

1.3计算方法及边界条件设置

计算采用雷诺时均N-S方程和RNGK-ε湍流模型，该模型已经在前面很多研究中取得了较好的结果。

进水池的进口设置为整个计算域的进口，采用质量流量进口条件；出水池的出口设置为整个计算域的出口，边界条件按压力条件给定：总压为一个标准大气压。叶轮为旋转域，其他设置为静止域，叶轮转速为1450 r/min。固体边壁表面包括：轮毂表面，叶片表面，叶轮外壳的内表面等，壁面采用无滑移的壁面处理，进壁区域采用标准壁面边界函数边界条件。进水流道出口与叶轮进口、叶轮出口与导叶进口为动静交界面，采用stage模型。

2计算结果及分析

通常认为评价进水流道的水力设计的标准包括以下三个方面的内容：第一，进水流道的流态是否良好，有没有产生有害漩涡（涡带）；第二，流道出口断面的速度分布是否均匀；第三，进水流道的水力损失的大小。下面将根据数值计算得到的数据分别从进水流道的流态，流道出口断面速度分布，水力损失和泵装置的性能等方面对三种方案进行对比分析。

2.1进水流道的流动基本特性

图4为计算得到的流态图（3D），由计算可知，钟形进水流道的水流运动过程可以分为三个阶段：水平收缩段，吸水室汇集段，喇叭管整流段。

水平收缩段：在直线段，水流从流道进口通过不断收缩来调整流态，以便均匀的进入吸水室。水流受流道内部边界场的约束，流线都是平行于水平方向，但在水深方向出现不同程度的弯曲。

吸水室汇集段：水流分为三部分，一部分直接从喇叭管前部进入喇叭管，另外两部分绕至喇叭管侧面、后面进入喇叭管。吸水室段的流态非常复杂，若流态不好，容易出现范围很大的漩涡。

喇叭管整流段：水流在喇叭管内部急剧收缩，流速迅速增加但因为受到导流锥的影响水流流速分布得到较快调整。

为直观的反映流场特性，截取断面A（图5）为特征面来分析。数值表明，不同流量工况下的流线分布大致相似，故只给出了设计工况下（Q=320L/s）三种方案进水流道断面A（进水流道底部以上0.8 cm处水平剖面）的流线图。

从图6可以看出以下结果。

（1）当流量Q=320 L/s时，三种方案的进水流道流线基本都是呈轴对称分布。方案1的流道后壁边角处流线非常紊乱且明显存在2个大漩涡和2个小漩涡；方案2的流道后壁处流线较不均匀，且有2个漩涡但范围相较于方案1明显缩小；相较于前两者，方案3的流道流线分布更规则，速度场更好，在后壁处出现2个范围很小的漩涡。

（2）半圆形吸水室相当于在矩形吸水室设置了一个起导流作用的半圆形隔板，“ω”形吸水室相当于在半圆形吸水室后壁顶端设置了一个起导流作用的隔舌。故“ω”形吸水室的流线最规则，半圆形吸水室次之，矩形吸水室最差。

2.2进水流道出口断面流速分布

图7为三种不同流量时，断面B（进水流道出口断面以下1.4 cm断面，见图5）的流速分布图。可以看出以下规律。

（1）在小流量至大流量各工况下进水流道出口断面流速分布并不均匀，在左右两侧流态基本对称，但是进水侧的流速明显大于后壁侧，呈月牙形分布，并非四周均匀进水。分布特征与已有的实验结果较为吻合，这表明采用的计算模型和方法是可靠的。

（2）小流量工况下，三种方案的后壁内侧均出现一个类似矩形的低速区，方案1低速区的范围较大，方案3低速区的范围较小，方案2的介于两者之间。大流量工况下，三种方案的后壁内侧均出现两个对称的局部高速区。只有方案1的后壁内侧出现低速区，但是低速区的范围与小流量工况相比小很多。

（3）同一工况下，三种方案的流场分布大致相似，形态稳定。方案1的流速变化梯度明显最大，方案2次之，方案3最小，这是流速均匀度差异的直观反映。同一工况，方案3的流速均匀性最好，方案2次之，方案1的均匀性最差。

2.3进水流道出口断面轴向流速分布均匀

度和速度加权平均角度

2.3.1进水流道出口断面轴向流速分布均匀度

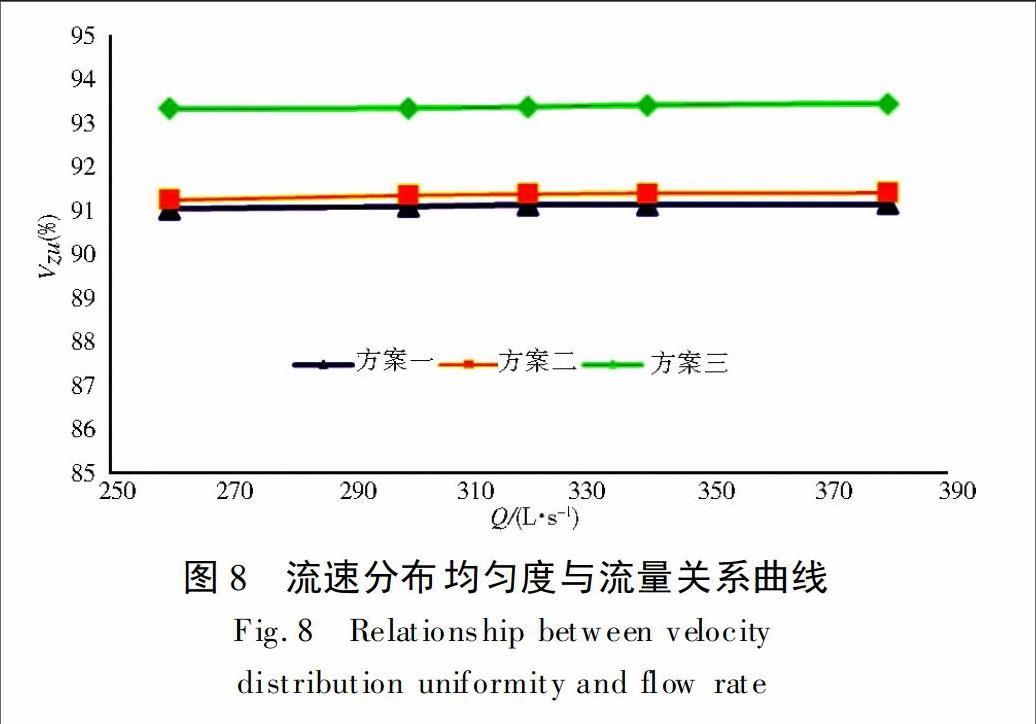
进水流道的出口就是叶轮室的进口，进水流道出口断面流速场是否均匀或者比较均匀会影响水泵运行性能。我们可以通过分析进水流道出口断面轴向流速分布均匀度来分析进水流道的设计质量。V_zu越大，则表明进水流道出口断面轴向流速分布越均匀，计算公式（1）如下：

图8给出了不同工况下，三种方案进水流道的出口断面轴向流速分布均匀度。可以看出恒定转速下进水流道出口断面轴向流速分布均匀度随着流量的增大而略有增加，但是增加值非常小。在设计工况（Q=320 L/s）下，轴向流速均匀度方案1为91.13%，方案2为91.37%，方案3为93.36%。比较数据可以看出，方案3的进水流道出口断面流速场最均匀，方案2次之，方案1最差。

2.3.2进水流道出口断面速度加权平均角度

进水流道出口水流的入流方向性会影响水泵的能量特性和汽蚀特性，我们可以通过分析进水流道出口断面速度加权平均角度θ来衡量好坏。O越大进水流道出口水流的入流方向性越好。

图9给出了不同工况下三种进水流道出口断面速度加权平均角度，计算结果表明流量Q在260L/s到380 L/s时，方案3的速度加权平均角度最大，均处在83.3°以上，方案1的速度加权平均角度最小，比方案2低0.4°，比方案3低0.6°，这说明方案三的进水流道出口水流的入流方向性最好。进一步分析发现θ实际上随着流量的增加而减小，但是幅度很小。

由此可知，对于钟形进水流道来说，其出口断面的流速均匀度和出口断面速度加权平均角度本身与进水流道吸水室后壁采用的具体形状有着非常密切的关系，而流量的大小对二者的影响较小。

2.4进水流道水力损失

轴流泵装置的特点是扬程低，这就导致流道的水力损失占装置扬程比值较大，对水泵装置效率的影响明显，所以装置的水力损失直接影响到工程的实际经济效益。当液体处于运动状态时，由于液体的粘滞性，在流动过程中液体内部会产生内摩擦力来阻碍液体间的相对运动，为克服这种阻力，流体中的一部分机械能会转化为热能，即产生水力损失。根据伯努利能量方程和RNG k-ε湍流模型计算得到的流速场和压力场来计算进水流道的水力损失，计算公式（3）-（5）如下：

图10表明进水流道的水力损失主要为吸水段水力损失，并且吸水段水力损失占总水力损失的百分比随着流量的增加而增加，故吸水段的尺寸和形状的合理设计对减少钟形进水流道水力损失具有重要意义。

图11表明流量Q在260 L/s到380 L/s时，进水流道水力损失随流量的增大而增大。相同流量下，方案1的进水流道水力损失最大，方案2次之，方案3的进水流道水力损失最小。方案2和方案3相当于在方案1的后避处添加了起导流作用的圆弧状隔板，故方案1的水力损失比方案2，方案3大。方案3相当于在方案2的中间加了导流作用的隔舌，隔舌可以截断水流的旋转，故方案3的水力损失比方案2小。各方案中，水力损失越小，断面流速均匀度越高。这表明方案3的进水流态较好，吸水室后壁形状设置合理。因此为了减少钟形进水流道进水流道的水力损失，吸水室后壁形状应采用“ω”形。

2.5泵装置效率与流量关系曲线

泵装置效率与流量关系曲线见图12，由图12可以看出以下规律。

（1）相同流量下，方案3的泵装置效率最高，最高效率达到了80.71%；方案2次之，最高效率为80.66%；方案1的泵装置效率最低，最高效率为80.26%。

（2）三种方案的泵装置Q-η曲线的变化趋势都是从最高效率点向两侧下降。大流量工况下，方案1的效率仅为72.22%，远远低于方案2和方案3，小流量工况亦是如此。高效区内，三种方案的效率较为接近。以方案3的最高效率点到75%为高效区。三种方案中，方案3的效率曲线变化最为平缓，高效区的流量范围较宽（262～380 L/s）；方案1的效率曲线变化最为陡峭，高效區的流量范围较窄（275～366 L/s）；方案2的效率曲线介于方案1和方案3之间，高效区流量范围适中（267～377 L/s）。方案3的高效区流量范围比方案2拓宽了7.3%，比方案1拓宽了30%。

3结论

（1）采用CFD数值模拟的方法，对包含了钟形进水流道，叶轮，导叶和虹吸式出水流道的全流道进行了数值模拟，反映了最为接近实际的泵装置流动情况。

（2）钟形进水流道的水平收缩段水流流线较为规则，流速分布较为均匀，水流流态良好；吸水室段和喇叭管整流段的流线并不规则，出现了漩涡，且流速分布并不均匀，虽然在左右两侧流态基本对称，但是进水侧的流速明显大于后壁侧。

（3）根据CFD性能预测的结果，当进水流道吸水室后壁形状采用“ω”形时，水力损失较小，水流流态较好，泵装置运行高效区流量范围比半圆形的拓宽了7.3%，比矩形的拓宽了30%。而矩形后壁吸水室和半圆形后壁吸水室内部的水流容易形成漩涡，增加进水流道水力损失，无法保证较好的进水条件，应该尽量避免采用。