破产理论在区域水量分配中的应用
2017-10-24李深林陈晓宏何艳虎白晓燕
李深林+陈晓宏+何艳虎+白晓燕

摘要:介绍了破产理论在区域水量分配问题中的应用。分析了传统破产理论在水量分配问题中的有效性和局限性,考虑配水单位水资源丰富程度、用水效率和最低供水保障率3个因素,对破产理论传统的分配规则进行优化改进,并实例应用于广东省东江流域各地市的水资源竞争性分配中。结果表明:(1)改进后的分配规则能综合考虑各分水单位水资源丰富程度和用水效率等各方面因素,合理排列分水单位的配水优先等级,确保高优先级单位水量供给,同时保证低优先级单位的最低供水标准;(2)面对未来不确定性来水条件,当可供水总量逐渐减少时,不同配水优先级单位具有不同的反应速率,高配水优先等级的配水单位其供水满足率的下降速率更趋缓慢,进一步体现了其优先配水地位。改进后的破产理论规则应用于区域水量分配中能够得到合理的分配结果,而且能根据问题的不同要求进行规则调整,极具灵活性,可以推广应用于其他地区。
关键词:破产理论;同损规则;水量分配;用水效率;东江
中图分类号:C934 文献标识码:A 文章编号:1672-1683(2017)05-0022-07
随着社会经济水平的发展,人类对水资源的开放利用程度越来越高,水资源紧缺问题也更趋紧迫。现阶段人多水少、水资源时空分布不均、经济社会发展与水资源分布不协调,以及日益严峻的水污染形势,使得实行合理有效的水资源管理方式成为迫切需求。在缺水情势下,对水资源进行合理分配成为缓解水资源供需矛盾和提高使用效率的重要途径。因此,设计合理的水资源分配方法具有重要实践意义,也吸引了大量科学家的研究,并取得了众多成果。其中,有利用水循环原理和水资源工程展开的配置研究;有基于社会管理学提出的相关管理模型,如胡晓寒,秦大庸等基于决策理论和博弈论建立水资源分配协商模型;有基于运筹学最优化方法来求解多目标函数,如史银军等采用了模拟寻优和遗传算法对灌区水量进行最优化分配;有基于经济学方法或概念来进行水量分配,如刘德地、陈晓宏借鉴基尼系数的基本内涵对区域用水量公平性开展评估。
然而,由于理论本身的理解难度或实际操作的成本问题,很多水量分配方法很难获得广泛的使用。考虑到这点,破产理论为区域水量分配问题提供了新的思路。
所谓破产,是指当债务人的全部资产不足以清偿到期债务时,债权人通过一定程序将债务人的全部资产供其平均补偿,从而使债务人免除不能清偿的其他债务,并由法院宣告破产解散的一种制度。在资产偿还过程中,因为可供分配的资产总量无法满足对每个债权人的全部补偿,为了将有限资产公平地分配给每个债权人而产生的分配规则称之为破产理论。
将破产理论应用于水资源分配问题中主要有以下两点原因:(1)破产问题的基础设定即可分配的资产总量不足以偿还所有债务,而水资源分配问题的基本矛盾是可分配的水资源总量无法满足所有用水户的需水要求,两个问题的基本设定极其相似;(2)破产理论分配规则相对简单,更易于水資源分配问题的决策者以及分配单位的使用.
正因如此,近年来破产理论在水资源分配中的应用逐渐引起了国内外学者的关注,如Beard对破产理论和河道水资源分配问题的关系进行了探讨;Madani和Dinar将破产理论应用到地下水管理当中;Ansink和Weikard从破产理论中发展出一系列可持续分配规则,并将其应用到水资源管理当中;H.Mianabadi和E.Mostert等研究了考虑各用水单位自身产水量下的破产理论;G.M.Sechi和R.Zueea则将用水单位的用水效率纳入破产理论考量参数,以划定各用水户的配水优先等级。Seem和Zucca研究了在设计供水缺口条件下破产理论对水资源的分配效果,并做了详细分析;孙冬营等运用破产理论尝试解决因水资源短缺而产生的跨行政区水资源配置冲突。
破产理论在区域水资源分配中的应用在国际上尚属于探索阶段。本文试图对破产理论的经典规则进行改进,纳入水量分配问题中需要综合考虑的各个因素,提高破产理论在区域水资源分配应用中的适用性和灵活性。
1研究方法
破产问题的由来是因为在分配过程中可供分配的总资源量无法全部满足每个成员的补偿需求,所以需要依靠某种分配规则,以保证资源分配的公平性。假设某破产问题中,各变量之间具有以下关系:
由上可知,破产理论中的PROP规则与水量分配中的同比例缺水率控制原则基本相同,都通过管控相同的缺水率使缺水带来的破坏损失平均地分摊给各个成员单位。而PROP和CEL规则都具有浅宽破坏原则的思想,通过共同承担损失而降低损失对每个成员的破坏程度。然而,CEL规则中,由于各需水单位平等承担的缺水量,当Y较大ci较小时,可能导致该需水单位大比例缺水,甚至零配水,从而造成其严重损失。所以,在具体运用时,还需做一定的改进。
1.2对破产理论分配规则的改进
区域水资源分配问题虽然本质上和破产问题十分贴合,但也存在传统破产问题所不具有的特点,所以在引入破产理论分配规则时,需要结合区域水量分配的具体情况进行规则的调整,使其尽量满足水资源配置遵循的有效性、公平性和持续性原则。
第一,流域水量分配问题和破产问题中,各成员单位既是资源的需求者,也是资源的产生者(破产问题中的待分配资产来源于各债权人的借贷,而流域的可分配水资源量来自于各分水区域的河川径流),然而,破产问题中债权人的补偿需求和借债数量是等值的,而水量分配问题中分水单位的用水需求和自身水资源丰富程度却并不一致。经典破产理论在强调补偿需求这一参数的同时,涵盖了对借贷数量的考虑,而区域配水问题中,需水量却不能表达水资源丰富程度的信息。所以将破产理论应用于水量分配中时,除了考虑用水需求大小之外,还要将各单位自身的水资源丰富程度作为水资源分配的一个参考依据,对于水资源总量大,水资源丰富度高的单位,其水资源需求应该得到更大程度的满足。
第二,一般破产问题中对资产的合理分配即为问题的完结,并不需要对资产分配后产生的效益负责。然而在水资源分配问题中,某水资源分配方案的实施是否能带来最优化的生产效益是决策者必须要考虑的问题之一。鉴于不同用水地区的生产力水平和用水效率的不同,分配相同数量的水资源产生的效益也会因地而异。为了充分反映水资源分配问题的这一性质,本研究将各地区的用水效率作为一个新增参考指标纳入破产理论分配规则中,对于水资源用水效率高的需水单位,其水资源需求将得到更大程度的满足。endprint
第三,水资源作为基本的生存和生产资源,分配过程中需要满足需水单位对水资源的最低要求,而破产问题却不需要对此做出限制。本研究在原破产理论规则基础上,增设最低供水保障率,即用水单位必须被供给的用水量占该单位总需求的比例。当根据其他因素计算得到的供水满足率小于最低供水保障率时,该单位将被配给最低供水保障率所规定的水量。最低供水保障率对应不同需水单位以序列岛的形式给出(见表1),具体取值根据具体流域管理经验、管理目标以及缺水严重程度进行有针对性的设定。
因此,本研究将区域水量分配上述三个特点纳入到破产理论的分配规则之中。
考虑水资源配置问题中三个因素之后,将破产理论中的同损规则进行调整如下:
区域水量分配问题不仅是主观决策问题,还需要考虑各成员单位客观的水资源开发利用条件。例如需水单位的水资源利用工程能力条件应作为配水量的约束条件配水量应小于地区的最大水资源开发利用能力。又例如存在跨流域调水的区域,应具体考虑跨流域调水的供给对象及其对各地需水量ci的影响;如果是水资源调出流域则要考虑调出水资源对各需水单位水资源丰富程度fi的影响。
2实例应用
2.1研究区域
本文以广东省东江流域为例,研究破产理论在区域水量分配中的应用。东江是珠江流域的三大水系之一,发源于寻邬桠髻钵山,干流流经河源、惠州、东莞等市,在东莞石龙经东江河网区汇入狮子洋,流域面积35 636 km2。东江是河源、惠州、东莞和广州市东部等沿海城市主要的生产和生活水源地f图1),同时通过跨流域调水供应深圳和香港地区的生产生活用水。随着受水区经济社会的迅速发展,水资源的需求大幅增加,水资源供需矛盾日益突出。流域内不均衡的发展状态也给水资源配置带来挑战。
根据广东省水资源公报,东江流域多年平均径流量326.6亿m3,年最大取水量为106.64亿m3。流域内各行政区分区年径流量如表2所示。河源市和惠州市年径流量大,分别为131.99和114.22亿m3,其他城市年径流量均较小,在20亿m3左右。本研究采用工业万元增加值用水量作为用水效率指标,其他产业用水效率暂未综合考虑。
2.2结果分析
正常来水年份可供东江河道外分配使用的年最大取水量为106.64亿m3,其中11亿m3必须供给香港,剩余95.64亿m3供东江流域内其他地市进行分配。在该可供水量減少10%、15%和20%这三种缺水情形下,本研究利用破产理论的三种经典分配规则和改进后的同损规则(CEL′)分别进行水量分配,并对可供水量减少10%条件下的分配结果以及不同程度缺水条件下分配结果的变化情况进行了分析。为便于讨论,本研究将各地市最低供水保障设为均值。同时考虑到本研究中存在可供水量减少20%的情景,最低供水保障率设置过高将导致该情境调节失效,过低则没有起到供水保障的作用各缺水条件下,所以选定80%作为河源,韶关,惠州,东莞,广州和深圳的最低供水保障率。
2.2.1可供水量减少10%条件下的分水结果
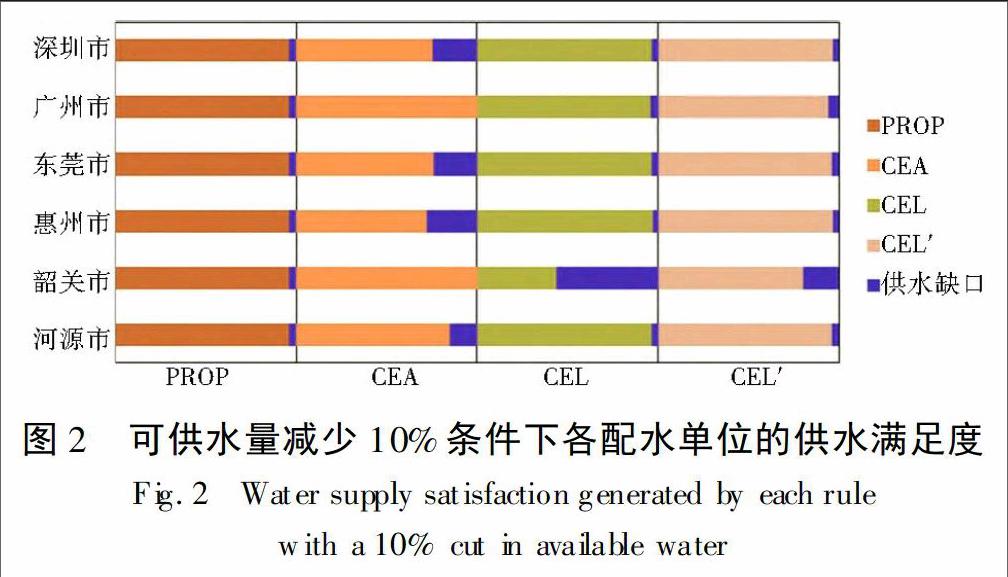
当可供水量减少10%时,各地市总用水需求8Q 67亿m3,可分配水量86.08亿m3,存在供水缺口,不能够百分之百满足各个地市的用水需求。运用破产理论的各种分配规则得到的水资源分配结果见图2。
PROP分配规则将可分配水总量和需水总量的比例照搬分配给各需水单位,得到亏空比例一致的分配结果。如图2所示,各需水单位供水满足率均为96%,存在4%的供水缺口。由于东江流域内地区发展十分不平衡,PROP规则下发达城市(如深圳、东莞)与发展中城市(如河源、韶关)配给得到相同满足度的分配结果,很难被流域管理部门采用。
基于CEA规则的水量分配将优先满足小需求用水单位。从表2看出,广州(增城)和韶关(新丰)的需水量少于其他城市,在CEA规则下,其用水需求也优于其他城市得到满足。相反,大需水单位的供给则受到抑制。如实例中深圳、东莞和惠州等城市的用水需求满足率都低于80%。
CEL规则对需求量小的用水单位抑制强烈。如图2所示,在该规则下,需水量极小的韶关市的供水满足率仅为45%,而其他高需水单位的满足率普遍较高,都达到95%以上。该分配结果的不足之处在于对韶关市的供水满足率过低,很难保证其基本的用水需求,容易引发社会问题。
CEL′规则以需水量为基础,综合考虑水资源丰富程度、用水效率和最低供水保障率等因素,对各个需水城市进行了合理的配水优先级排序。惠州市本身需水量最大,同时水资源丰富程度高,用水效率也较高,成为优先配水城市,供水满足度最高,达到97%;深圳市自身需水量也很大,尽管本地水资源丰富程度低,但是因其极高的用水效率而成为优先供水城市,供水满足度达到97%;河源市水资源丰富程度高,而用水效率较低,东莞市水资源丰富程度较低,但用水效率较高,两市最终配水优先级排在惠州和深圳市之后,为96%;广州市(增城)本身需水量较低,而且水资源丰富程度和用水效率与以上四市都存在一定差距,配水优先度明显居后,配水满足度降为94%;韶关市(新丰)在各个因素的综合考量中没有任何与其他城市竞争的优势,供水满足率本应该很低,然而由于最低供水保障率的设定,也配给了80%的需水量。
由此可见,在可供水量减少10%的条件下,改进后的CEL规则能根据各个需水单位的水资源丰富程度以及用水效率等特征,合理安排其配水优先等级。具有高优先级的需水单位配水满足度较高,而最低供水保障的引入,保证了低配水优先级的单位得到最低保障供水。与破产理论的经典规则相比,CEL′具有较大的优势。endprint
2.2.2不同程度缺水情形下的水量分配变化
当可供水量减少10%、15%甚至20%时,各个地市由于供水优先等级不同,其供水满足度的变化情况也存在不同。
如图3所示,在PROP规则下,各需水单位始终按照绝对平均比例配水,不同缺水条件下的供水满足率始终与总供需水的比例相同,各地市之间不存在变化差异;CEA规则始终优先满足小用水户的用水需求,导致在缺水越来越严重的情况下,大需水用户的供水满足率快速降低;CEL规则会忽视小用水户的用水需求,在缺水渐趋严重时,为保证大需水单位保持较高的供水满足率,小用水户的供水量会迅速下降,甚至零配水。
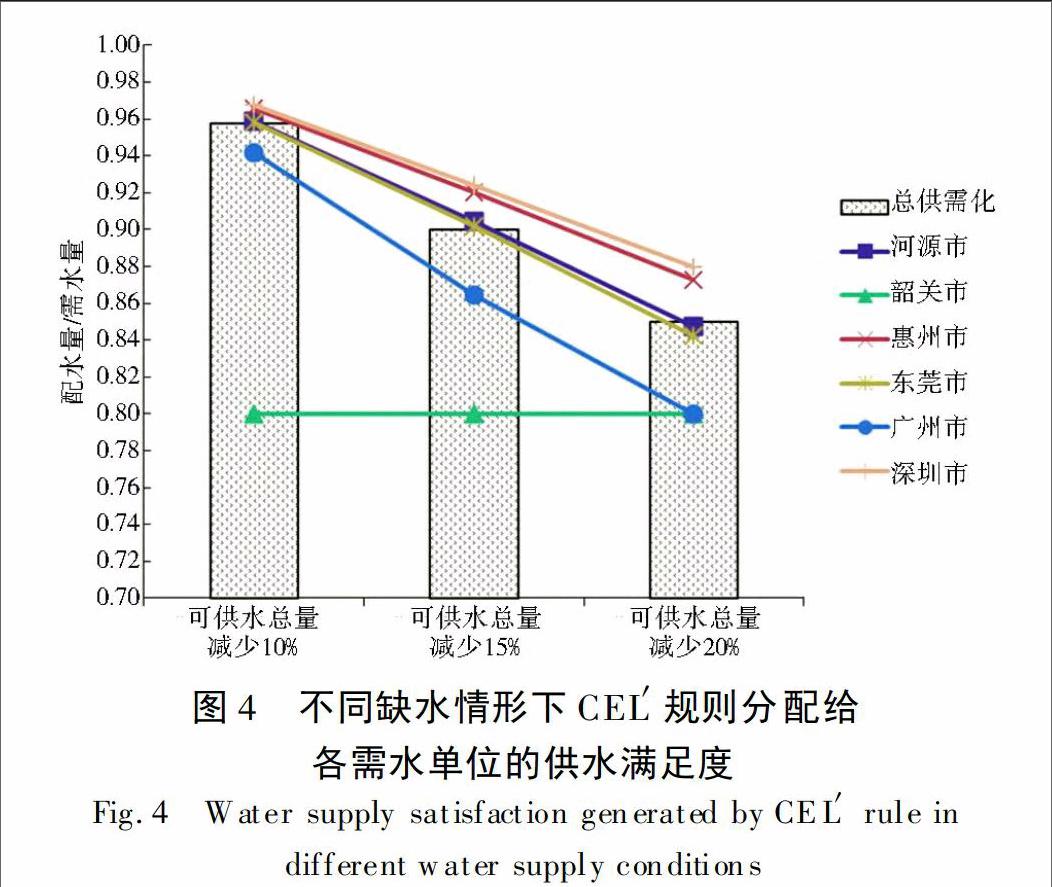
相比之下,CEL′规则能得到更为合理的分配结果。在面对未来不确定情形下,CEL′规则综合各个影响因素,合理赋予各个需水单位不同的配水优先等级。具有高配水优先等级的单位不仅会获得更高的配水满足率,而且在可供水量逐渐减少的情况下,供水满足率的下降速率更趋缓慢(图4)。
深圳市和惠州市在CEL′规则下被赋予了高配水优先等级。各来水条件下,深圳市的供水满足率分别为97%、92%和88%,惠州市为97%、92%和87%,明显高于其他四个城市在相同缺水条件下的配水结果,也高于96%、90%和85%的总供需比例。另一方面,当可供水量逐渐减少,深圳市和惠州市供水满足率的下降速率也低于总供需比的下降速率。这样的分配结果充分体现了其在水量分配中的优先位置。
东莞市和河源市在CEL′规则下的分配优先级别属于中等。在不同来水频率情形下,其分配结果与总供需比基本相同,供水需水满足率的下降幅度也与总供需比的下降趋势十分接近。
广州市(增城)属于下等配水优先级。各个来水条件下,广州市(增城)的供水满足率均低于总供需比例。再者,当总供水缺口较小时,广州市(增城)配水满足率稍低于总供需比,而当总供水缺口扩大,其供水满足率快速下降,下降速率超过总供水缺口变大的速率,如图4所示,可分配水量减少10%时,广州市(增城)的供水满足率为94%,与总供需比以及东莞和河源市基本接近,而可分配水量减少15%时,广州市(增城)的供水率已经显著低于总供需比,可供水总量减少20%时,该用水单位更是成为最低用水保障单位。
韶关市在CEL′规则中,一直属于最低用水保障单位。
3讨论
破产问题的基础设定和水量分配问题及其相似,但其经典分配规则不能完全满足水量分配的要求。其经典分配规则如PROP、CEA和CEL等,都是以需定供,应用于需要综合考虑其他因素的复杂的水资源分配问题时,存在较明显的缺陷。例如,CEA规则总是优先满足小需水单位的用水需求,而CEL规则会优先满足大需水单位,并导致小需水单位的用水需求存在很大的缺口。PROP规则下各单位按照相同的亏空比例配水,这样得到的结果在多数情况下也不能让决策者满意。
改进后的破产理论分配规则能够更加全面地考虑区域水量分配问题中的各影响因素,得到更加合理的分配结果。在充分考虑各用水单位的需水要求,并引入水资源丰富程度,用水效率和最低供水保障率等参数之后的分配规则能够较好地区分各个用水单位的配水优先等级:水资源丰富程度和用水效率高的用水单位将获得较高的配水优先等级,其用水需求将得到更大的满足。比如实例研究中的深圳市,用水需求量最大,而且用水效率极高,具有绝对的优势,所以在分配结果中其需水满足比例也很高。而另一方面,最低供水保证率的存在保证了配水优先等级靠后的用水单位能够获得最低保障的配水。
再者,相比于其他研究对破产理论分配规则的改进方法,本研究的改进方法更加全面。H.Mi-anabadi和E.Mostert將配水单位水资源丰富程度作为调节参数,水资源越丰富的用水单位就将获得更高的配水满足率,G.M.Sechi和R.Zucca的研究考虑了水资源产出效益的影响。本研究在参考前人研究成果的同时,将水资源丰富程度和用水效率两个因素统一纳入考虑,并新增了最低供水保障控制这一指标,实例研究表明,改进后的规则得到的分配结果更为合理。
此外,对CEL′规则的使用灵活性可以在今后做进一步研究。从式(13)可以看出,通过增设年径流量或用水效率的权重系数,可以分别调整该参数对分水量结果的影响程度;通过对最低供水保障率的不同设定,也将对整体分配结果产生较大影响。良好的灵活性将扩展破产理论在区域水量分配问题中的使用广度,适应不同区域分水的实际情况,以满足决策者的不同需求,得到最能满足实际需要的分水方案。
虽然本研究通过新增参数,理论上增加了破产理论在区域水量分配问题中的可靠性,然而在实际应用中,具体参数的确定仍然需要进一步研究。尤其是如何科学衡量其综合用水效率,以及合理确定最低供水保障等问题需要在后续研究中进行探讨。
4结论
(1)经典的破产理论分配规则,包括PROP、CEA和CEL规则,面对需要多方面考虑的复杂的区域水量分配问题时,存在一定的缺陷。
(2)改进后的同损规则能够较好的适用于水量分配问题。本文在CEL规则的基础上,考虑区域水资源丰富程度,用水效率和最低供水保障率三个调节参数。实例研究显示,采用改进后CEL规则的分配结果能够综合考虑各个用水单位的基本情况,得到合理的优先配水等级。具有高优先级的需水单位得到了配水满足度更高。而最低供水保障率的设定,保证了低配水优先级的单位得到基本用水需求。
(3)在CEL′规则下,具有高优先级的需水单位不仅在一定来水条件下得到较大的配水满足度,而且,随着可供水量的减少,其配水满足度的下降速率也低于低优先级的配水单位。
(4) CEL′规则的函数构造形式,使得决策者可以根据决策要求和配水问题的实际情况,对各影响要素的权重进行调节,从而得到最能满足实际需要的分水方案,这也扩展了破产理论在区域水量分配问题中的使用广度。endprint
