直驱风电接入后对电力系统小干扰稳定性影响分析

，

(1.内蒙古电力集团有限责任公司，内蒙古 呼和浩特 010000；2.东北电力大学电气工程学院，吉林 吉林 132012)

直驱风电接入后对电力系统小干扰稳定性影响分析

任振宇1，张师2

(1.内蒙古电力集团有限责任公司，内蒙古 呼和浩特 010000；2.东北电力大学电气工程学院，吉林 吉林 132012)

建立了永磁直驱同步风机数学模型，基于PSAT搭建了WSCC-3机9节点模型，并分析了该类型风机接入系统对系统小干扰稳定性的影响。通过分析可以得出结论，无论直驱同步风机接入什么位置，随着直驱同步风机出力增加，传统火电机组出力减少，系统各个振荡模式的阻尼比均增加，从而可以提高系统小干扰稳定性。

全球能源互联网;风力发电;永磁直驱同步风机;小干扰稳定;阻尼比

1 引言

随着全球能源互联网的提出，推动清洁能源发展满足全球电力需求已成为越来越多学者关注的重点[1]。目前现有的可再生能源发电包括风力发电、太阳能发电、潮汐发电等等，其中目前技术最成熟的是风力发电[2]。

随着风电装机容量的日益增加，截至2015年底，我国风电装机容量达1亿千瓦，其中2015年新增1474万千瓦。目前研究表明，电网受到扰动后，风电机组的位置、类型、运行工况等均会对系统稳定性有重要影响[3-5]。文献[3-4]采用Matlab工具箱PSAT分析了不同类型的风电机组对系统功角稳定性的影响。文献[5]分析了不同位置的双馈风电机组(Double Fed Induction Generator,DFIG)对系统功角稳定性的影响，提出寻找关键风电场位置并改变该位置的风电机组工况以提高系统功角稳定性的方法。

永磁直驱同步风机(Direct Drive Synchronous Generator,DDSG)作为第三代的风电机组，相对于第一代的恒速异步风机(Constant Speed Wind Turbine)、第二代的DFIG，具有噪声小、运行效率高、运维成本低等优点[6]，目前在我国风电市场的占有率正逐年增加[7]。目前针对DDSG并网系统的稳定性问题研究并不多，因此直驱风电接入对系统小干扰稳定性的影响是一项亟需研究的工作。本文在对DDSG建模的基础上，采用PSAT分析了DDSG并网对电力系统小干扰稳定性的影响。

2 DDSG数学模型

DDSG的结构示意图如图1所示，DDSG模型主要分为以下几个部分：原动机模型、发电机模型、换流器模型和控制模型。

图1 DDSG发电系统结构图

2.1 原动机模型

DDSG的原动机捕获的机械功率P为：

(1)

其中：ρ为空气密度；Cp为风功率利用系数；Ar为扫风面积；vw为风速。

2.2 发电机模型

发电机定子电压直轴分量vds、交轴分量vqs分别可以表示为：

vds=-rsids+ωmxqiqs

(2)

vqs=-rsiqs-ωm(xdids-ψp)

(3)

其中：ωm是DDSG的电气转速；ids、iqs分别为定子电流直轴分量和定子电流交轴分量；rs为定子电阻；xd、xq分别为定子直轴电抗和定子交轴电抗；ψp为定子磁链。

由于有换流器的存在，因此近似认为原动机是同轴的，转子运动方程可以简化为[8]：

(4)

其中：Tj为惯性时间常数；ω为转子转速；Tm、Te分别为发电机的机械和电磁转矩。

2.3 换流器模型

换流器的动态过程与机电过程相比要快得多，因此，环流器模型被简化为理想电源。

换流器发电机侧的有功Ps和网侧的有功Pg可以表示为：

Ps=vdsids+vqsiqs

(5)

Pg=vdgidg+vqgiqg

(6)

其中：idg、iqg分别为网侧电流直轴分量和网侧电流交轴分量；vdg、vqg分别为网侧电流直轴分量和网侧电流交轴分量。

换流器发电机侧的无功Qs和网侧的无功Qg可以表示为：

Qs=vqsids-vdsiqs

(7)

Qg=vqgidg-vdgiqg

(8)

2.4 控制模型

DDSG的电压控制模型如图2所示。通过测量的机端电压与参考电压的偏差来对网侧电流直轴分量idg调节，从而控制DDSG输出的无功功率。

图2 DDSG电压控制模型

此外，DDSG还有最优风功率捕获功能，因此配备桨距角控制，如图3所示。

图3 DDSG桨距角控制模型

当转速变化时，通过此时的转速判断桨距角在什么开度能使风功率捕获最大，从而控制桨距角大小。

3 电力系统小干扰分析

电力系统可以用一组非线性微分方程和一组非线性代数方程来表示：

(9)

式中：xk为系统的第k个变量;t为时间。

根据Lyaponov线性化理论，可以用线性化系统的稳定性来研究实际非线性电力系统的稳定性。在运行点x0附近进行线性化处理，可以表示为初始值xk0与微增量Δxk之和，即：

xk=xk0+Δxk

(10)

在x0附近展开成泰勒级数并消去非状态变量和微增量的高次项，系统方程可以表示为：

Δx=A·Δx

(11)

式中:A为n×n维系数矩阵，也称状态矩阵，它的特征根决定了系统的小干扰稳定性[9]。

机电振荡模式的阻尼比ζ是衡量系统小干扰稳定的一个指标，由特征值可以计算得出：

(12)

其中：α为特征根的实部；β为特征根的虚部。当特征根实部α为正，阻尼比ζ为负，受到扰动后会使系统振荡发散，不能回到新的稳态平衡点；反之，当特征根实部α为负，阻尼比ζ为正，受扰后系统会振荡衰减，最后达到一个稳态平衡点。

4 DDSG接入对电力系统小干扰稳定性的影响

本文研究DDSG接入电力系统的小干扰稳定问题采用Matlab工具箱PSAT，PSAT在分析电力系统稳定性方面的有效性已经在文献[10]中得以验证。

本文结合WSCC-3机9节点算例分析DDSG接入对系统小干扰稳定性的影响。系统图如图4所示，在分析DDSG接入电力系统后的小干扰稳定性问题时，可以将风电场采用一台风电机组等值以简化计算[11]。本算例中风电场为100台2MW的DDSG。

采用特征根分析法分析在不同位置接入不同出力的DDSG，相应减少bus1的火电出力，对系统小干扰稳定性的影响。仿真结果如表1所示。

图4 WSCC 3机9节点系统

从表1可以看出无论在什么位置接入DDSG减少bus1火电机组出力，随着DDSG出力的增加，各机电振荡模式的实部均远离虚轴。此外，相同工况的DDSG接入不同位置后，系统机电振荡模式的特征根也不同。

表1 机电振荡模式特征根

设bus1、bus2、bus3的火电分别为#1号、#2号、#3号发电机，图5、图6分别为#3-#1机电振荡模式、#2-#1机电振荡模式的阻尼比。

从图5、图6可以看出，在各个母线接入DDSG后，随着DDSG出力增加，bus1火电出力减少，两个机电振荡模式的阻尼比均增加。此外，从仿真结果可以看出，当DDSG接入到bus4、bus5、bus6时，DDSG出力的增加对主导振荡模式(#2-#1振荡模式)的阻尼比并无太大影响。

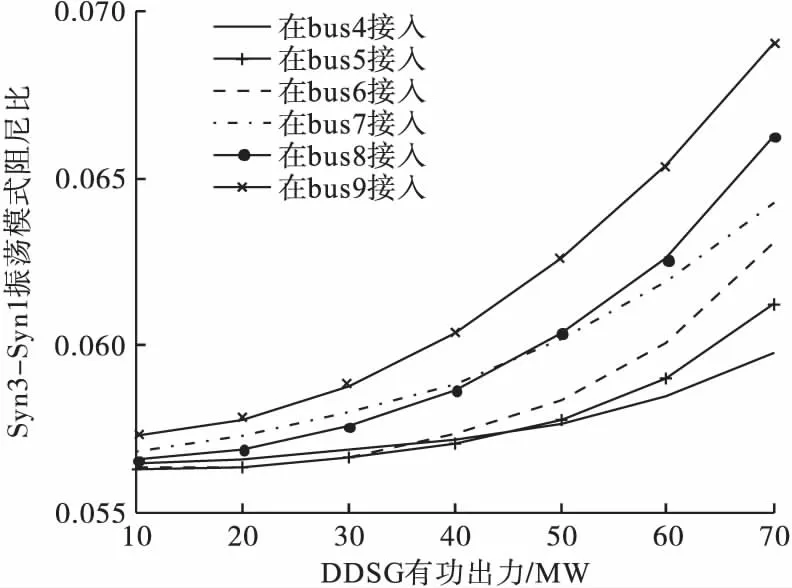
图5 #3-#1振荡模式阻尼比

图6 #2-#1振荡模式阻尼比

从图4可知，bus4、bus5、bus6与Syn1较近，因此在bus4、bus5、bus6接入DDSG，减少bus1出力，并不会对初始潮有太大影响，而在bus7、bus8、bus9接入对初始潮流的改变较大，从而影响了线性化的结果，导致特征根变化较大。

从以上分析可知，DDSG型风机接入电力系统后，无论DDSG接入何种位置，随着DDSG的出力增加，火电机组出力减少，系统机电振荡模式的阻尼比增加，提高系统的小干扰稳定性。当DDSG离同步机较远时，DDSG出力变化对该台同步机的机电振荡模式影响较小。

5 结论

本文基于PSAT对永磁直驱同步风机(DDSG)进行建模，在此基础上，分析了不同位置接入不同容量DDSG对系统小干扰稳定性的影响。通过分析可知，无论DDSG接入什么位置，DDSG出力增加，火电机组出力减少，系统各个机电振荡模式的阻尼比均增加，从而有利于提高系统小干扰稳定性。因此，DDSG可以代替传统同步发电机接入，从而提高系统的小干扰稳定性。

[1] 刘振亚.全球能源互联网[M].北京：中国电力出版社，2015.

[2] Jose′ Luis Dom′,et al.Power oscillation damping supported by wind po=wer:A rev1iew[J].Renewable and Sustainable Energy Reviews，16(2012)：4994-5006.

[3] 张师，于昊，张梦雅，等.大规模风力发电并网对系统小干扰稳定性的影响[J].广东电力，2014，27(12):15-18.

[4] 赵祥，张师，周毅博，等.风火打捆交直流混联送端系统暂态稳定性分析[J].智能电网，2015，3(7):594-602.

[5] Eknath Vittal,Andrew Keane.Identification of Critical Wind Farm Locations for Improved Stability and System Planning[J].2013,28(3):2950-2958.

[6] 高峰,周孝信,朱宁辉,等.直驱式风电机组暂态 建模及仿真[J].电网技术,2011,35(11):29-34.

[7] 叶瑞丽，刘瑞叶，刘建楠，等.直驱风电机组风电场接入后的电力系统暂态稳定计算[J].电工技术学报，2014，29(6):212-219.

[8] 郝元钊.风力发电机组对电网稳定性影响的研究[D].湖南：湖南大学，2011.

[9] KUNDUR P.Power System Stability and Control[M].New York：McGraw-Hill Inc，1994.

[10] Federico Milano.An Open Source Power System Analysis Toolbox[J].IEEE Transactions on Power Systems,2005,20(3)：1199-1206.

[11] Fernandez L M,Saenz J R,Jurado F.Dynamic Models of Wind Farms With Fixed Speed Wind Turbines[J].Renewable Energy,2006,31:1203-1230.

EffectofDDSGWindTurbinestoPowerSystemSmall-signalStability

RENZhen-yu1,ZHANGShi2

(1.Inner Mongolia Electric Power Refco Group Ltd，Hohehot 010000,China；2.Northeast Dianli University，Jilin 132012，China)

The mathematical model of direct drive synchronous generator is established.Based on the PSAT,the WSCC-3 machine 9 bus model is built,and the influence of the type of wind turbine grid to system on the stability of small signal stability is analyzed.Through the analysis can be concluded,regardless of direct driven synchronous generator access what position,with direct driven synchronous gnerator output increase,traditional thermal power unit output decrease,damping ratio of different oscillation modes of the system was increased,which can improve the small signal stability of the system.

global energy internet;wind power generation;direct drive synchronous generator;small signal stability;damping ratio

1004-289X(2017)02-0057-04

TM71

B

2016-01-14

任振宇(1987-)，男，汉族，工程师，2013年毕业于东北电力大学电气工程专业，研究方向电力系统动态安全分析；张师(1989-)，男，汉族，助理实验师，2015年毕业于东北电力大学电气工程专业，研究方向电力系统动态安全分析。