数形结合思想在数学解题中的运用

◎谭子灏

数形结合思想在数学解题中的运用

◎谭子灏

数形结合是高中阶段的重要解题思想，在实际问题解决中的应用价值较高，能提升问题解决质量与效率。学生在高中阶段的数学课程学习过程中，应当加强对该解题思想的应用研究。本文简要就数形结合思想在实际问题中的解题策略进行分析，并以此为基础，总结性的探索了该解题思想的实际应用模式。以期为广大高中学生的数形结合思想应用能力提升提供参考，保证解题质量。

数形结合思想主要是指学生在实际问题解决时，通过就数与形之间的相互关系进行分析，将题目中理解较为困难抽象的条件与关键点通过形象的集合图形进行表示。从而实现复杂的问题简单化，帮助学生找准问题解决的关键点，避免重复冗长的问题分析与计算，是重要的高中数学问题解决工具。该解题思想的应用相比其他解题方式更加有效，学生在实际问题解决时不仅能实现解题精确度的提升，还能有效实现解题时间的节约。

数形结合思想在实际数学问题解决中的应用分析

数形结合思想作为重要的数学解题思想，在高中数学问题解决中的应用是十分常见的，在多种问题解决中都具有重要的应用优势，且具体表现在以下几方面数学知识的解决中。其一，集合类问题的解决。集合是高中阶段的重要数学知识内容，在高考数学试题的选择与填空题中十分常见，而其大多是以就集合的交集、并集以及补集的方式出现。学生在进行该类型的问题解决时可采用数形结合思想进行问题解决，即利用数轴展开问题思考，将抽象的集合问题具体化，方便学生快速地得到问题答案。

例1，现存在一全集为U=N，集合A={X=2n,n∈ N},B={X|X=4n,n∈ N}，试求出集合U=( )。

学生可根据题目绘画出相应的Venn图来就问题中的数据关系进行表示，从而求出相应的集合。如图1所示，B集合其实是A集合的真子集，所以集合U=A∪CuB。

图1

其二，方程与不等式问题的解决。方程问题与不等式问题不仅可作为单独的计算问题，同时还可能会出现在综合性数学题当中，学生在就方程问题进行解决时可将其转化为函数交点问题，而不等式问题可转变为函数问题。之后再利用函数的几何意义来绘制相应的几何图形，从而实现问题解决。

例2，试求方程组x+y=3,y=2x这一方程组的解。

学生在就该方程问题解决时，可根据方程数据将其变化成图像交点图形，即图2，并根据交点的坐标来就该方程组的解的大小进行明确，从而进行问题解决。最终解出该方程组的解为x=1,y=2。

图2

其三，绝对值问题的解决。学生在就绝对值问题进行解决时可通过数形结合的思想，将绝对值问题中的数值转换到相应的数轴上，依靠绝对值性质确定解题范围，从而求解。

例3，当|x|＞a,(a＞0)，试求x的取值范围。

学生在就该问题解决时，可首先根据题干中的数据绘制出相应的数轴图，即图3，由两点之间的具体可分析得出x的取值范围为：x＜-a或者x＞a.

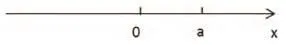
图3

数形结合思想的解题应用模式分析

由数据变化为图形。高中阶段的数学问题对于学生的抽象思维与逻辑思维的能力要求较高，所以大多数的题目中给出的数据与条件都较为抽象，利用代数解题方式实现问题解决将难以抓住问题解决的关键点。学生在进行该类型的问题解决时就可根据问题中涵盖的数据进行数据变形，将其转化为图形。首先，学生应当就实际问题中的条件以及结果进行分析，积极调动所学的几何与立体几何知识进行问题中的数据重现，绘出相应的图形。并就该图形的性质以及几何意义进行标明，之后再根据具体的图形表达式或者相关公式来进行问题解决，求出问题目标。

由图形变化为数据。图形问题逐渐成为当前高中数学考察中的重要类型，但是在实际问题中所涉及到的图形往往十分复杂，学生可将相关图形转变为具体的数据，通过代数法来进行问题的解决。而为保证图形转化的准确性，学生应当首先就题目中的图形特征进行分析，观察该题目中是否存在隐含性条件。而在实际问题解决时，学生应当遵循以下解题规律。即首先就题目要求与问题求解目标进行明确，其次在就图形中所含有的几何意义与几何条件进行分析，最后利用代数式进行图形数据与条件的表达，利用所学的代数公式或者代数定理进行问题求解。

使数据和图形相互变化。该解题模式的应用从本质上讲，其实就是以上两种解题模式的有机结合体，其主要被应用于更为复杂的数学问题当中。该类型的问题往往不仅含有较多的抽象的数据，同时还以复杂的图形作为已知条件。学生在进行该问题解决时，应当就实际问题进行深入的分析，并就题干中所给出的数形关系进行标注。注意观察题目中是否存在隐含性的条件，养成数据与图形相互变化的意识。

数形结合思想在高中数学问题解决中的应用十分广泛，能就常见的集合问题、不等式问题、三角函数问题、线性规划问题以及绝对值问题等进行解决，相比其他解题方式更加快速便捷。而学生在实际问题解决的过程中，还应当注重由数变形、以形变数以及数形互变等多种解题模式的应用，切实实现自身的数形结合思想的应用能力提升，保证问题解决的质量与问题解决的效率。

（作者单位：长沙市雅礼中学）