基于神经网络的发电机调速系统控制方法

龚喜文， 许 辉

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

基于神经网络的发电机调速系统控制方法

龚喜文， 许 辉

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

在目前实际的船舶电力系统中，同步发电机组的调速系统依旧采用传统的比例-积分-微分(Proportion Integral Derivative,PID)控制策略，但由于同步发电机组具有较强的耦合性和非线性特点，常规的PID控制策略很难达到良好的效果。为改进PID控制策略的不足，提出小脑模型(Cerebellar Modal Articulation Controller,CMAC)-PID并行控制方法。该方法利用CMAC神经网络自我学习、自我适应和自我组织的能力来提高PID控制策略的性能，其优良的性能效果已在MATLAB/Simulink建模仿真中得到验证。

发电机；比例-积分-微分；调速系统；神经网络

0 引 言

随着船舶的大型化和自动化程度不断提升及电力推进技术的逐步成熟，对船舶电力系统容量的要求愈来愈高。此外，大量的电压敏感负荷(如PLC控制器、微机系统及补偿装置等)应用于船舶电力系统中，对船舶电网电能质量提出了更高的要求，船舶电网中的电能质量与电力系统中的稳定控制密不可分。发电机组控制系统是保证整个电力系统稳定的核心，其中调速控制系统和励磁系统控制着机组的端电压及其转速，对保证船舶电力系统的稳定运行和可靠控制起着关键作用。

目前，实际中船舶发电机调速系统大多仍采用传统的比例-积分-微分(Proportion Integral Derivative,PID)控制策略，由于发电机组的非线性较强，控制效果并不理想；而人工神经网络(Artifical Neural Network,ANN)具有自学习、自适应和自组织的能力，因此将小脑模型(Cerebellar Model Articulation Controller)神经网络引入到调速系统中，能改善PID控制策略的不足。此外,为更全面地体现出CMAC-PID控制策略的优越性能，引入BP(Back Propagation)网络，并在不同工况下对3种控制策略进行综合仿真。试验结果表明，CMAC-PID控制策略能有效提升发电机调速系统的性能。

1 调速控制策略

1.1神经网络算法

目前，ANN作为一种新型智能型控制方法，已在控制系统中得到一定的应用。这主要是因为ANN在理论上具有逼近任意非线性映射的能力，对于一个输入信号，其多个神经元可并行地根据一定的规则调整自身参数，控制输出数据，因而具有自适应的能力。与一般的控制方法相比，人工神经网络具有以下特点：

1) 作为典型的非线性系统，可较为精确地处理数据的拟合；

2) 可对较难用数学公式或物理模型定义的模型进行分析和处理；

3) 可并行处理数据，应用于实时性较高的场合；

4) 可同时处理类型相异的数据，较强地组合各类信息。

ANN可从函数逼近的角度分为全局型的网络和局部性的网络。全局逼近网络是指该网络的输出取决于网络中的每个神经元的阈值和权值;而局部逼近网络指的是输出只取决于不多的几个神经元的变化，与全局逼近网络相比是一种区域范围内的变化起作用。ANN中应用最为广泛的BP算法属于全局逼近网络，而CMAC,RBF和B样条网络属于局部逼近网络。根据理论分析，CMAC与另外2种网络相比，基函数最为简单，应该具有最快的响应速度[1]。选择将CMAC网络引入到发电机组调速系统中[2]，为验证CMAC网络是否比其他神经网络中作用于调速系统的控制效果要好，引入BP网络作为对照。在调速系统中，神经网络与PID控制共同调节参数。

1.2BP-PID并行控制算法

BP网络是一种按误差逆传播算法训练的多层前馈网络，能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。其主要思想是:输入学习样本，采用反向传播算法对网络的权值和偏差进行反复的调整训练，使输出的向量与期望向量尽可能地接近，当网络输出层的误差平方和小于指定的误差时,训练完成，保存网络的权值和偏差。BP-PID在实际控制中可分为2个模块：

1) PID控制器仍处于主导状态，该模块为闭环调节模块；

2) PID的参数是BP网络经过学习的过程而最终作为输出量输入到PID中，BP网络以2个输入量和1个误差作为输入[3]。

并行控制过程见图1。

1.3CMAC-PID并行控制算法

CMAC神经网络是一种表达非线性函数的表格查询型自适应神经网络，由1个固定的非线性输入层和1个可调的线性输出层组成[4]。CMAC网络在处理数据时，首先把输入的信息分布式存储在神经元中，每个神经元的值取0或1。CMAC的输出值是通过存储单元的值相应加权得到的；将期望值与该值作减传回输入层，从而修改权值[5]。由于CMAC网络在每个数据输入时只需调整少量的连接权值，因而响应速度较快。CMAC与PID复合控制结构见图2。

在控制时，常规PID控制器实现反馈控制，保证系统的稳定性，对扰动起抑制作用；CMAC神经控制器实现前馈控制，实现被控对象的逆动态模型。系统控制算法为

(1)

u(k)=un(k)+up(k)

(2)

式(1)和式(2)中:αi为输入状态的存储单元；c为存储单元个数，即泛化参数；un(k)为CMAC相应的输出；up(k)为常规PID的输出。

CMAC的调整指标为

(3)

(4)

w(k)=w(k-1)+Δw(k)+a(w(k)-w(k-1))

(5)

式(3)～式(5)中:η为网络学习速率，η∈(0，1)；a为惯性量，a∈(0，1)。

设定存储神经元的权值为0。在仿真开始后，常规PID起主要调节作用；随着CMAC网络初始化的完成，神经元的权值开始逐渐增加，进入到网络的自学习阶段;网络学习一段时间后，完成整个系统的控制，PID控制不再有效，控制器总输出即为CMAC网络的输出。

2 调速控制策略的仿真

MATLAB软件工具具有强大的功能，其中的Simulink工具箱可运用于船舶电力系统高精度仿真中[6]。Simulink工具箱中包含多种函数和模型抽象成的模块库，能较为方便地搭建船舶电力系统模型并进行相关仿真[7]。

2.1船舶电站系统的模型

根据实际的船舶电站系统的结构，在Simulink环境下搭建船舶电站系统总体模型(见图3)[1]。

在系统中，包括2台发电机组：

1) 转换装置配置成傅里叶模块；

2) 负载模块有RLC并联的静态负载和异步电动机的动态负载2类。

由于船上静态负载多呈感性，因此将RLC并联负荷中的电容值配置为0。

船舶电力系统的模型搭建完成后，在Simulink仿真环境下进行相关试验，主要包含发电机的空载启动试验和加减负载试验2部分。

2.2发电机空载启动试验

进行发电机空载启动试验的主要目的是验证BP-PID并行控制策略和CMAC-PID并行控制策略的可行性。调速系统作为被控对象，其传递函数的表达式为

(6)

在BP-PID并行控制策略中,BP网络参数设置为：η=0.25;α=0.05。在CMAC-PID并行控制策略中,CMAC网络参数设置为：N=300;C=8;η=0.3;α=0.04。仿真系统的输入信号为方波信号，BP-PID和CMAC-PID都对输入信号进行跟踪调速，仿真结果见图4。

由图4可知:BP-PID和CMAC-PID控制策略能控制发电机的调速系统，两者的控制效果比较接近，无法体现出CMAC-PID控制策略的优越性。

2.3发电机加减负载试验

进行发电机加减负载试验的主要目的是区分常规PID,BP-PID和CMAC-PID等3种控制策略的调速效果。不同调速系统的调速效果能通过柴油发电机的输出功率和转速来反映。

在仿真过程中，通过改变断路器1的开关状态来模拟加减负载。在3次不同的控制策略下，发电机组的转速曲线和输出功率曲线分别见图5及图6。

比较发电机组调速性能的动态指标有瞬时调整率和稳定时间。

1) 瞬时调整率指柴油发电机组突加(或突减)全负荷后的瞬时最小转速(或瞬时最大转速)与负荷改变之前的额定转速之差同额定转速的比值的百分比,其计算式为

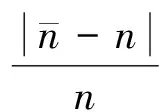
(7)

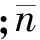
2)稳定时间是指从突加(或突减)全负荷后转速刚偏离额定转速至恢复到额定转速的波动范围所需的时间,其计算式为

ts=tb-tp

(8)

式(8)中:tb为转速恢复到标定转速的时刻;tp为转速刚偏离额定转速的时刻;ts为稳定时间。

比较图5中的3种控制方式下的发电机转速曲线，在第4 s断路器闭合、负载接入柴油发电机后，通过计算可知：常规PID瞬态调整率为4.5%，稳定时间约为3 s；BP-PID并行控制瞬态调整率为4.2%，稳定时间约为2.4 s；CMAC-PID并行控制瞬态调整率为3.8%，稳定时间约为2 s。在第8 s断路器断开后，通过计算可知：常规PID瞬时调整率为4.3%，稳定时间约为1.8 s；BP-PID并行控制瞬时调整率为4.1%，稳定时间约为1.7 s；CMAC-PID并行控制瞬时调整率为3.8%，稳定时间约为1.6 s。结合图6可知：对于相对复杂的系统，神经网络和PID并行与传统PID相比，控制效果明显，响应速度较快；而CMAC-PID并行控制与BP-PID并行控制相比，控制效果更好，响应速度更快，更加适合实时性较高的场合。

3 结 语

本文利用MATLAB/Simulink搭建船舶电站系统的模型，同时在该模型上对一种基于CMAC-PID的发电机调速系统控制方法进行仿真。仿真结果表明，提出基于CMAC-PID的发电机调速系统控制方法可提高发电机调速系统的精度和准度,提升船舶电力系统的稳定性。

[1] 张伟，朱大奇，孔敏，等．基于改进的CMAC神经网络与PID并行控制的研究[J]．计算机测量与控制，2005,13(12)：1359-1360．

[2] 石勇，齐自达，张连瑜，等．基于CMAC神经网络前馈控制的柴油发电机组转速控制研究[J]．内燃机工程，2014，35(2)：98-101．

[3] 丁茂森，张艳．船舶柴油发电机转速的BP-PID并行控制[J]．船电技术，2012，32(12)：15-18．

[4] 尹维生，李岩．CMAC-PID在柴油机调速系统中的应用[J]．计算机仿真，2010，27(12)：200-202．

[5] 时文飞，侯世英，李学远，等．基于CMAC与PID复合控制的柴油机调速系统[J]．自动化技术与应用，2006，25(4)：11-13．

[6] 施伟锋，许晓彦．船舶电力系统建模与控制[M]．北京：电子工业出版社，2012．

[7] GRANELLI G, MONTAGNA M．MATLAB Implementation of the Complex Power Flow[J]．The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2013，32(3)：923-935．

NeuralNetworkBasedGeneratorSpeedRegulationSystem

GONGXiwen，XUHui

(State Key Laboratory of Navigation and Safety Technology, Shanghai Ship & Shipping Research Institute, Shanghai 200135, China)

The traditional Proportion-Integral-Derivative (PID) control strategy is used for speed control of synchronous generator in actual ship power systems nowadays. But due to strong coupling and nonlinear characteristics, it is difficult for conventional PID control strategy to achieve good results in speed control of synchronous generators. In order to improve the performance of the PID control strategy, this paper proposes Cerebellar Modal Articulation Controller(CMAC)-PID control method for that purpose in stead of conventional PID control strategy. The CMAC neural network, featuring self learning, self adaptation and self organization, improves the performance significantly. The design is verified through MATLAB/Simulink modeling and simulation.

generator; PID; speed control system; neural network

U665

A

2017-05-04

龚喜文(1978—),男,江西宜丰人,高级工程师,硕士,主要从事舰船自动化研究。

1674-5949(2017)03-0042-04