基于滑动势能面的二维材料原子尺度摩擦行为的量化计算∗

史若宇 王林锋 高磊 宋爱生 刘艳敏 胡元中 马天宝†

1)(清华大学,摩擦学国家重点实验室,北京 100084)

2)(南京航空航天大学航天学院仿生结构与材料防护研究所,南京 210016)

3)(北京科技大学腐蚀与防护中心,北京 100083)

基于滑动势能面的二维材料原子尺度摩擦行为的量化计算∗

史若宇1)王林锋2)高磊3)宋爱生1)刘艳敏1)胡元中1)马天宝1)†

1)(清华大学,摩擦学国家重点实验室,北京 100084)

2)(南京航空航天大学航天学院仿生结构与材料防护研究所,南京 210016)

3)(北京科技大学腐蚀与防护中心,北京 100083)

近年来,二维材料优异的摩擦特性成为人们关注的焦点,然而目前缺乏理论上对其摩擦力进行快速、有效、精确的计算预测方法.本文提出采用密度泛函理论计算真实体系的滑动势能面,利用得到的“数值型势能面”替代传统的解析势函数,并结合Prandtl-Tomlinson模型,量化求解具有复杂形状势能面的真实二维材料体系的摩擦行为.基于该方法,揭示了原子力显微镜实验中观察到的石墨烯Moiré纹超晶格结构的双周期“黏-滑”摩擦现象;理论预测了二维材料异质结构的层间超低摩擦现象,相对于同质材料,其静摩擦力和滑动摩擦力均成数量级降低,发现势能面起伏和驱动弹簧刚度均会影响层间相对滑动路径,进而对层间的摩擦行为产生影响.该方法同样可拓展到其他van der Waals作用主导的界面摩擦体系.

原子级摩擦,Prandtl-Tomlinson模型,二维材料,层间滑动

1 引 言

随着科学研究尺度的微观化和技术应用的纳米化,原子尺度的摩擦行为一直受到科研人员的广泛关注.原子力显微镜(atomic force microscopy,AFM)是研究原子级摩擦行为的重要手段,探针基座通过悬臂梁带动探针针尖在样品表面滑动,通过测量和记录悬臂梁的扭转变形得到针尖和样品之间的摩擦力.Prandtl-Tomlinson模型［1,2］(PT模型)可以在理论上很好地描述AFM的实验过程,将探针基座、悬臂梁、针尖分别简化成驱动块、弹簧以及振子,将样品表面原子的势能起伏简化成三角函数的形式,那么这一过程就可以被抽象成一个可以解析的动力学过程即PT模型:一个匀速运动的驱动块通过弹簧带动一个振子在三角函数的势能面上滑动,振子感受到的势能包括两个部分,一是振子受到基底作用的势能,二是弹簧中的弹性势能.对PT模型建立动力学方程并求解,可以分析体系的摩擦行为,即在给定的势能面、弹簧刚度、温度等条件下,能够获得每一时刻振子的位置、驱动块所受到的力以及系统各部分的能量等详细信息,从而为人们研究原子级摩擦行为和能量耗散机制提供指导［3,4］.

近年来,二维材料呈现出许多新奇而优异的摩擦特性,例如重构表面或二维材料异质结构会出现摩擦力的调制现象,显著影响体系的摩擦特性和能量耗散［5−7］,特别是二维材料层间的超滑状态［8,9］,使其成为纳米摩擦学研究中的热点.二维异质材料或二维材料层间的滑动势能面往往难以用简单的解析型函数(如三角函数)来描述,因而限制了人们采用经典PT模型对其摩擦特性进行理论计算.另一方面,分子动力学方法可以直接模拟原子尺度的材料摩擦行为,特别是在石墨烯体系中得到了广泛应用.然而分子动力学方法依赖于层间作用势的合理选取,对于实际中大量二维材料体系尚缺乏有效的经验势函数描述其层间相互作用.本文采用由密度泛函理论(DFT-D)计算的“数值型势能面”替代简单的解析势函数,实现对二维异质材料表面和层间摩擦行为的求解.利用DFT-D计算可以精确得到任意体系滑动势能面离散化的数据,将其处理为可用于PT模型计算的“数值型势能面”,从而可以计算其摩擦行为.我们采用这一方法,研究了单原子在石墨烯和金属钌构成的异质结构表面的摩擦行为,发现了与AFM实验中相近的双周期黏滑现象.利用第一性原理得到的二维材料层间滑动势能面,研究了二维材料层间的摩擦行为,发现二维异质材料的层间静摩擦力和动摩擦力远小于同质材料之间的摩擦力,详细分析了石墨烯层间滑动时的滑移路径以及刚度对摩擦力的影响规律.这一基于数值型势能面的差分法求解PT模型的研究手段,可以适用于各种二维材料,以及层间以van der Waals作用为主的界面摩擦问题,同时有助于深层次揭示原子尺度摩擦和能量耗散的物理本质.

2 方 法

2.1 PT模型计算

PT模型中,摩擦副的上表面简化为速度为v的驱动块,通过刚度为k的弹簧带动质量为m的振子,下表面一般简化为三角函数形式的势能面于是滑动的过程中体系的总势能为

其中,x为t时刻振子的位置.于是,振子的动力学过程可以由朗之万(Langevin)方程表达:

式中m为振子质量,µ为系统的阻尼系数,ξ(t)为温度项.基于MATLAB采用四阶的龙格-库塔方法对方程进行求解,由于本文不讨论温度的影响,求解过程中将温度设为0 K,ξ(t)=0.对方程(2),求解每一时刻的振子位置x,进一步可以得到每一时刻的摩擦力F,即驱动块受到的弹簧力:

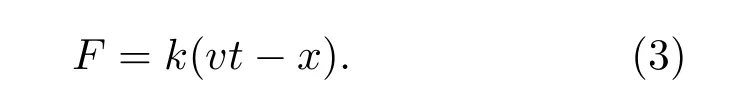
但在很多情况下,实际的势能面不是简单的三角函数形式,甚至难以准确写出其数学表达式,也就不能进行计算.为了突破这一方法的局限性,等间隔地建立势能-位置的“数值型势能面”:U(x)=(U1,U2,···Un),这一势能数据库精度足够高(间隔∆x足够小)时,差分可以得到势能导数-位置的数据库:

每一步求解过程中,利用上一步得到的振子位置在数据库中读取势能导数的数值,代入本步进行求解.本文将这种解法称为差分法,而将以往所用的方法称为微分法.

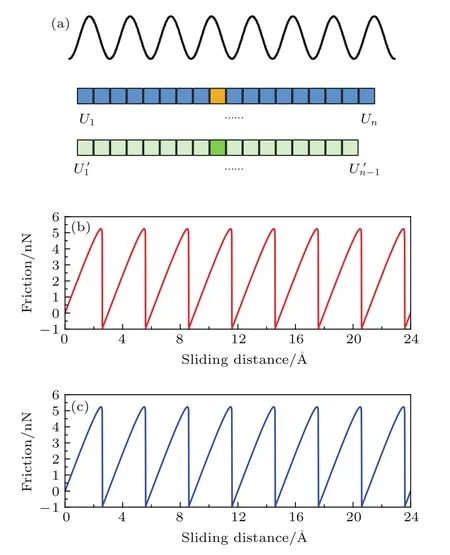
图1 (网刊彩色)(a)势能面、势能库和势能导数库示意图;(b)差分法得到的黏滑曲线;(c)微分法得到的黏滑曲线Fig.1.(color online)(a)Schematics of potential surface,potential data base and potential derivative data base;(b)friction obtained via fi nite di ff erence method;(c)friction obtained via di ff erential method.

经验证,采用差分法和微分法在相同的时间步长下得到的结果基本相同.采用一个正弦函数形式的势能面进行测试,势能面的周期为3 Å,幅值为5 eV,分别用差分法和微分法在同样的条件下(弹簧刚度k=30 N/m,温度T=0 K,阻尼系数0.6,驱动块速度v=10−5m/s,振子质量m=10−12kg,对于差分法势能库格子取0.01 Å)进行计算,得到了如图1(b)和图1(c)所示的黏滑曲线,对比发现两者平均差距仅0.12%.

差分法也可以应用于二维的势能面,二维的动力学方程为:

此时势能导数也要扩展至二维:

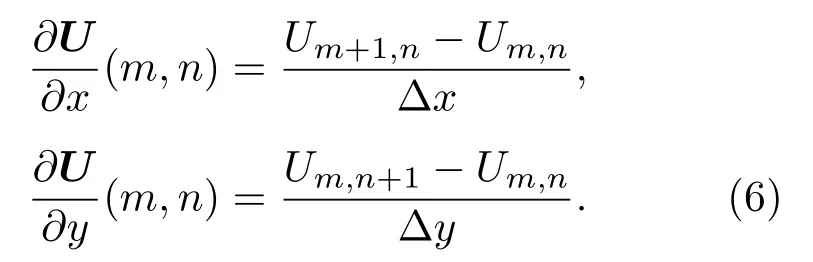
振子受到两个方向上的力:

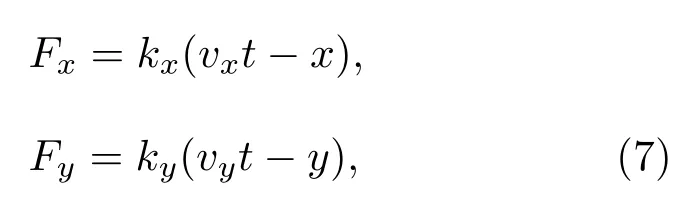
其中kx,ky代表弹簧在x,y两个方向上的刚度,在AFM实验中分别是垂直探针悬臂长轴的刚度和沿着长轴方向的刚度.AFM的摩擦实验中针尖一般沿着垂直探针悬臂长轴的方向滑动,因此将探针悬臂受到的扭转力作为摩擦力,本文二维势能面的求解中,也采用驱动块在x方向上的弹簧力Fx作为摩擦力.

2.2 DFT计算

PT模型中所需的数值型势能面由DFT-D计算得到.所用方法为具有长程色散作用校正的密度泛函理论计算方法［10−12］,交换关联泛函采用广义梯度近似中的Perdew-Burke-Ernzerhof泛函［13］.价电子和离子实之间的作用采用投影缀加波方法［14,15］描述,截断能为400 eV.总能的收敛精度为10−4eV.计算优化并记录两层材料处于不同的相对位置时的体系势能,得到体系的滑动势能面.对势能面插值扩展之后可用于PT模型差分求解摩擦行为.

3 结果与讨论

3.1 针尖在异质结构表面的摩擦行为

两种不同的二维材料之间若具有晶格失配或者相对转角,叠在一起会形成一种称为Moiré纹(Moiré pattern)的周期结构［16］. 事实上,Moiré纹是一种广泛存在的超晶格结构,不仅限于二维材料之间.最近Zhu等［17］模拟发现,表面电荷可以改变水分子的偶极取向,从而调控水的结构相变.研究表明,水分子在冰相下呈现六方结构,并可与石墨烯形成公度或者不公度结构,并形成Moiré纹结构.这样,在异质结构表面就形成了两种周期性势能面的叠加,一种是原子晶格周期的势能面,另一种是Moiré纹周期的势能面.由于势能面比较复杂,这种结构会呈现出一些新奇的摩擦行为［6,7］.石墨烯Gr晶格周期为aa=2.46 Å,金属Ru晶格周期为2.71 Å,Gr和Ru构成异质体系便会出现Moiré纹［18,19］,并且AFM实验中发现了双周期“黏-滑”摩擦现象,如图2(a)所示［20］.Gr蜂窝状的原子结构使得其势能面分布也是蜂窝状,再叠加上一个Moiré纹周期的势能面,这种二维的势能面极为复杂,很难准确写出表面势能的数学表达式,采用微分法计算比较困难,于是我们用差分法对这一体系的摩擦行为进行研究.

首先通过第一性原理软件(VASP)建立并优化Gr和Ru的异质结构,二者构成的Moiré纹周期为am=3 nm［21］.导出表层Gr的原子位置和Moiré纹中心的位置.然后以每个碳原子位置为中心生成一个高度为Ua0、半径为aa的原子级势垒:

以每个Moiré纹中心位置生成一个高度为Um0半径为am的势垒:

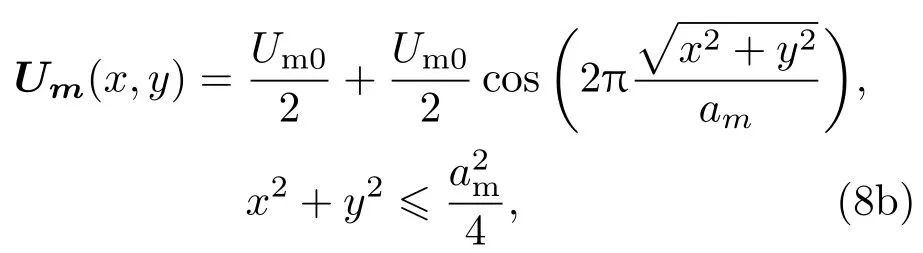
其中Ua0,Um0根据实验中Fmax确定,这样就构成了整个异质结构体系的势能库,如图2(d)所示.

这里势能库x和y方向的格子均为0.05 Å,Ua0=16 eV,Um0=120 eV,aa=0.246 nm,am=3 nm,x和y方向的弹簧刚度分别为kx=35 N/m和ky=150 N/m,温度为0 K.得到的摩擦力图如图2(e)所示,从中可以看出原子晶格的周期性特征和Moiré纹大小的周期性特征,从图2(g)的侧向力曲线中也可以看到原子晶格周期和Moiré纹周期的两种黏滑特征.Gr和Ru之间的作用力比较强,二者所形成的异质结构表面Moiré纹级的势垒较大,会发生双周期的黏滑.除此之外,Gr和锗Ge［6］、铂Pt形成的异质结构［22］,KBr和NaCl形成的异质结构［7］,以及表面重构的金Au［5］,表面都会出现或强或弱的摩擦力调制现象,均可用差分法PT模型进行摩擦行为的分析.

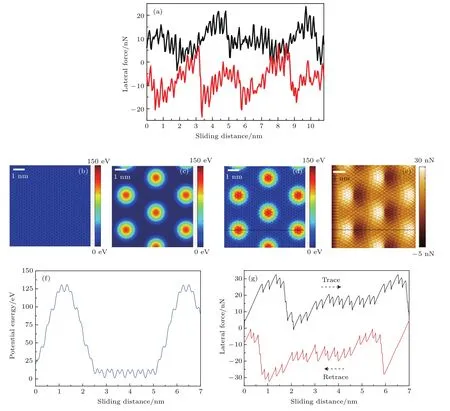
图2 (网刊彩色)(a)AFM实验中的黏滑曲线;(b)只有原子晶格势垒的势能面;(c)只有Moiré纹势垒的势能面;(d)异质结构的势能面,由(b)和(c)叠加而成;(e)由异质结构的势能面得到的摩擦力图;(f)图(d)中黑色虚线上的势能分布;(g)图(e)中黑色虚线上的黏滑曲线［20］Fig.2.(color online)(a)Experimental Friction loop;(b)potential surface with atomic-level barrier;(c)potential surface with superlattice-level barrier;(d)potential surface with both atomic-level and superlattice-level barriers;(e)friction map corresponding to the potential surface in(d);(f)potential energy pro fi le;(g)calculated friction loop corresponding to(f)［20］.

3.2 二维材料层间的摩擦力

两层二维材料在不公度接触的情况下,每个原子受到来自不同方向不同大小的力相互抵消,层间滑动势垒很小,有可能出现超滑行为［23］.这里,我们利用第一性原理计算了二维材料的层间滑动势能面［9］,并输入差分法PT模型,计算各个体系的摩擦力,研究二维材料层间的摩擦行为.

3.2.1 不同二维材料之间的摩擦行为

图3(a)—(e)是第一性原理计算得到的各个材料层间滑动势能面,相对于二硫化钼(MoS2)、石墨烯(Gr)、氟化石墨烯(FG)和各自同质的材料层间滑动势能面,FG和MoS2以及Gr和MoS2之间因不公度性的存在,势垒很小.

基于上述的滑动势能面,我们通过差分法计算了在这几种的体系下各自的摩擦力图,如图3(f)—(j)所示,类似AFM实验中摩擦力图的做法,将势能面等分为若干条水平线,沿着水平线从左向右滑动,得到这些水平线上的摩擦力,进而将各条线组合成一幅摩擦力图.从图3中可以看出,在同质结构的体系里,MoS2/MoS2体系的势能面起伏最大,相应的摩擦力也较大,而FG/FG体系的势垒和摩擦力相对较小.而对比同质的体系,异质材料之间摩擦力则小很多.图4中定量地对比了各个体系的势垒高度和摩擦力大小,FG/MoS2和Gr/MoS2的摩擦力量级在10−4nN,与同质体系相比可以忽略不计.由于这两种异质体系能垒非常小,二者进入了一种称为连续滑动的状态［5］,这时两者之间不发生黏滑失稳,去程和回程的摩擦力曲线基本重合,因此摩擦力和能量耗散均极小,发生超滑.而另一个值得注意的是,尽管MoS2/MoS2体系势垒比Gr/Gr体系大,但MoS2/MoS2体系周期较大,使得两种势能面梯度相近,在PT模型中,最大摩擦力和势能面梯度直接相关:Fmax=πU/a,因此二者摩擦力基本相同.

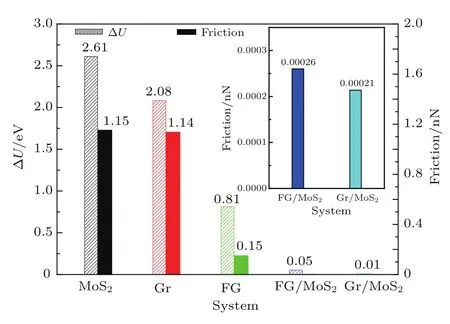
图4 (网刊彩色)MoS2/MoS2,Gr/Gr,FG/FG,FG/MoS2和Gr/MoS2体系的势垒和摩擦力对比Fig.4.(color online)Potential barrier and friction of MoS2/MoS2,Gr/Gr,FG/FG,FG/MoS2and Gr/MoS2.

3.2.2 摩擦过程中振子的运动路径

与一维不同的是,本文涉及x,y两个方向上的运动自由度,因此PT模型描述的驱动块在沿着x方向运动时,振子不仅在x方向上运动,在y方向上也会和驱动块的扫描路径发生偏移,因此振子的运动路径将是一条在平面上寻求最低总能量的曲线.对于层间滑动过程而言,二维PT模型中的振子轨迹代表了层间滑动时实际运动的相对路径,而驱动块路径是指外部驱动力的方向.为了对此做进一步的探讨,我们以Gr/Gr体系为例,计算了不同扫描路径下振子的运动轨迹.

图5(a)展示了驱动块沿着三条不同的路径运动时,振子每一时刻在势能面上的位置.路径1○是沿着晶格的密排方向跨过势能面最高点的直线,路径2○是沿着势能面较低位置的直线,路径3○是介于1○,2○之间的直线,经过势垒的半山腰.图中虚直线代表驱动块的运动轨迹.每隔固定的时间间隔,用圆点记录下振子的位置,圆点连线是振子的运动轨迹.由于这里的采样密度比较大,很多圆点出现了重合,因此我们将每条路径上的振子轨迹进行了不同程度的放大,分别列在图5(c)—(e)中,路径1○,2○,3○上的摩擦力如图5(f)—(h)所示.

从记录的振子路径数据上可以看出,振子大多时间在势能低点.在路径1○,振子路径虽然和驱动块在y方向上有偏移,但基本是一条直线,由于驱动块路径距离势能最低点较远,在弹簧力的作用下,振子不能处于整个势能面的最低点.此时,每一个黏滑周期中振子跳过一个晶格大小.而在路径2○,由于整个势能面最低点距离驱动块路线较近,弹簧对振子作用较小,因此振子可以从一个势阱跳跃到另一个势阱,并且在一个黏滑周期中,振子跳过半个晶格大小.由于路径2○上的势能起伏相对较弱,此时的摩擦力也较小.对于路径3○,振子轨迹也基本是一条直线,摩擦力曲线和路径1○比较接近.

3.2.3 y方向刚度对振子路径及摩擦行为的影响

振子的轨迹是势能面和弹簧的弹性势能共同作用的结果.这里涉及势能面的形状和弹簧的刚度等参数,前文已经讨论了势能面的形状对振子位置和摩擦力的影响,而弹簧刚度可以分为x,y两个方向,在AFM实验中分别是垂直探针悬臂长轴的刚度和沿着长轴方向的刚度,不同的AFM探针有不同的x,y方向刚度,以往的文献对x方向的弹簧刚度kx研究较多,这里借助二维PT模型,对y方向弹簧刚度ky和摩擦行为之间的关系进行进一步探讨.

图5 (网刊彩色)(a)Gr/Gr体系的滑动势能面,箭头和虚直线标记了驱动块的运动路径,圆点标记了振子的实际轨迹,相邻圆点间等时间间隔;(b)图(a)中势能面对应的摩擦力图;(c)—(e)图(a)中三个振子路径的放大,横坐标为x方向的位置,y坐标为偏离各自驱动块路径的距离;(f)—(h)三条路径各自对应的摩擦力曲线Fig.5.(color online)(a)Sliding potential surface of Gr/Gr,arrows and dashed lines indicate the direction of the driver,black dots indicate the trajectory of the oscillator,time intervals are constant between adjacent dots;(b)corresponding friction map;(c)–(e)trajectory after zooming in on(a),axis X indicates the driver’s position in x direction and axis Y indicates the oscillator’s shift in y direction away from the trace of the driver;(f)–(h)friction loop on di ff erent trajectories.

图6 (网刊彩色)(a)—(d)在Gr/Gr体系滑动势能面上分别标注了y方向刚度为200 N/m,50 N/m,10 N/m,1 N/m时驱动块不同路径下振子的轨迹;(e)—(h)y方向刚度分别为200 N/m,50 N/m,10 N/m,1 N/m时对应的摩擦力图;(i)—(l)分别对应(a)—(d)路径3○上的摩擦力曲线Fig.6.(color online)(a)–(d)Trajectory of the oscillator when spring constant on y direction is 200 N/m,50 N/m,10 N/m,1 N/m;(e)–(h)friction map corresponding to(a)–(d);(i)–(l)friction loop on trace3○.

图6展示了ky不同时振子路径的变化,图6(a)—(d)分别是ky为200,50,10,1 N/m时振子的轨迹,而kx一直保持10 N/m.当ky很大时,随着振子在y方向上的偏移,弹簧的弹性势能积攒很快,总能量迅速增加,因此振子在y方向上的偏移很小,振子的轨迹近似为沿着驱动块路径的直线,并且不论驱动块沿着哪条路径运动,振子轨迹都是如此.ky的减小给振子y方向的偏移提供了条件,ky=50 N/m时,路径2○对应的振子轨迹开始发生偏移,振子的停留位置大多在势能最低点,而路径1○,3○对应的振子轨迹仍然保持直线.随着ky继续减小,振子的偏移也逐渐增加,当ky非常小时,振子受到弹簧y方向的约束很弱,此时,弹簧积累的弹性势能很小,下表面势能面的影响占据主导作用,从而振子被迫寻找势能面的最低点,因此即使在路径1○和3○上,振子也会沿着势能面上势能最低的路径运动,如图6(d)所示.而由于y方向刚度影响了振子的运动轨迹,投影在x方向上的振子轨迹也会发生改变,从而影响了体系的摩擦力.以路径3○对应的摩擦力曲线为例(图6(i)—(l),在ky较大时,黏滑周期和势能面的晶格周期相同,是比较规则的黏滑曲线.而ky=10 N/m时,由于在一个黏滑周期中,振子在更远处的一个势能低点有短暂的停留,因此黏滑曲线的突滑阶段并没有直接掉落至最低点,而是有一个微小的上升,之后才继续降低,最终进入另一个黏着阶段.当ky非常小时,无论驱动块沿着哪个路径运动,振子的轨迹基本相同,都是从一个势阱跳跃至下一个临近的势阱,因此每条线上的摩擦力Fx差别不大,都是在同样的位置发生黏着和突滑,也就出现了摩擦力图条纹状的特征.

4 结 论

利用DFT-D得到的“数值型势能面”替代简化的解析势函数,将PT模型计算摩擦行为的适用范围拓展至任意势能面,而非局限于规则的周期性简单势能函数,可量化求解具有复杂形状势能面的真实二维材料体系的摩擦行为,给原子级摩擦的研究提供了一个快捷可靠的计算分析手段.以此为基础,探讨了针尖和异质材料表面之间的摩擦行为,揭示了实验中的双周期黏滑现象的机理.同时,详细计算分析了不同二维材料层间的摩擦行为,发现异质材料之间摩擦力可以成数量级降低,讨论了层间滑动路径的变化规律,指出y方向刚度和摩擦行为之间有密切的联系,为二维材料间摩擦行为的预测提供了理论指导.上述通过差分法PT模型的计算和分析,为摩擦行为调控、超滑系统设计等提供了理论依据.

本文计算部分在清华信息科学与技术国家实验室“探索100”上进行.

［1］Tomlinson G A 1929Phil.Mag.7 905

［2］Zhao Y P 2012Surface and Interface Mechanics(Beijing:Science Press)p301(in Chinese)［赵亚溥2012表面与界面物理力学(北京:科学出版社)第301页］

［3］Dong Y,Vadakkepatt A,Martini A 2011Tribol.Lett.44 367

［4］Wang Z,Ma T,Hu Y,Xu L,Wang H 2015Friction3 170

［5］Li Q,Dong Y,Martini A,Carpick R W 2011Tribol.Lett.43 369

［6］Zheng X,Gao L,Yao Q,Li Q,Zhang M,Xie X,Qiao S,Wang G,Ma T,Di Z,Luo J,Wang X 2016Nat.Commun.7 13204

［7］Maier S,Gnecco E,Barato ffA,Bennewitz R,Meyer E 2008Phys.Rev.B78 045432

［8］Liu S,Wang H,Xu Q,Ma T,Yu G,Zhang C,Geng D,Yu Z,Zhang S,Wang W,Hu Y,Wang H,Luo J 2017Nat.Commun.8 14029

［9］Wang L F,Ma T B,Hu Y Z,Zheng Q,Wang H,Luo J 2014Nanotechnology25 385701

［10］Grimme S 2006J.Comput.Chem.27 1787

［11］Kresse G,Hafner J 1994Phys.Rev.B49 14251

［12］Kresse G,Furthmüller J 1996Comput.Mater.Sci.6 15

［13］Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865

［14］Blöchl P E 1994Phys.Rev.B50 17953

［15］Kresse G,Joubert D 1999Phys.Rev.B59 1758

［16］Geim A K,Grigorieva I V 2013Nature499 419

［17］Zhu X,Yuan Q,Zhao Y P 2014Nanoscale6 5432

［18］Pan Y,Zhang H,Shi D,Sun J,Du S,Liu F,Gao H J 2009Adv.Mater.21 2777

［19］Pan Y,Shi D,Gao H J 2007Chin.Phys.16 3151

［20］Shi R,Gao L,Lu H,Li Q,Ma T,Guo H,Du S,Feng X,Zhang S,Liu Y,Cheng P,Hu Y,Gao H,Luo J 20172D Mater.4 025079

［21］Gao L,Liu Y,Ma T,Shi R,Hu Y,Luo J 2016Appl.Phys.Lett.108 261601

［22］Filleter T,Bennewitz R 2010Phys.Rev.B81 155412

［23］Hirano M,Shinjo K 1990Phys.Rev.B41 11837

Quantitative calculation of atomic-scale frictional behavior of two-dimensional material based on sliding potential energy surface∗

Shi Ruo-Yu1)Wang Lin-Feng2)Gao Lei3)Song Ai-Sheng1)Liu Yan-Min1)Hu Yuan-Zhong1)Ma Tian-Bao1)†
1)(State Key Laboratory of Tribology,Tsinghua University,Beijing 100084,China)
2)(Institute of Bio-inspired Structure and Surface Engineering,College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
3)(Corrosion and Protection Center,Key Laboratory for Environmental Fracture(MOE,University of Science and Technology Beijing),Beijing 100083,China)

The excellent tribological characteristics of two-dimensional(2D)materials have

great attention,however,how to e ff ectively predict their frictions is still lacking.Here,we propose to obtain the sliding potential energy surface by density functional theory calculations,instead of simpli fi ed potential energy function.Thus it is able to solve the frictional behaviors of 2D materials with irregular complex potential energy surfaces.Firstly,we reveal the mechanism of dual-scale stick-slip behavior between a tip and a graphene/Ru(0001)heterostructure.With a dual-wavelength potential energy surface,we observe a similar frictional behavior to those captured in atomic force microscopy experiments,in which a signi fi cant long-range stick-slip sawtooth modulation emerges with a period coinciding with the Moiré superlattice structure.Secondly,we discuss the interlayer frictions of 2D materials,including graphene/graphene, fl uorinated graphene/ fl uorinated graphene,MoS2/MoS2,graphene/MoS2and fl uorinated graphene/MoS2.With sliding potential energy surface obtained by density functional theory calculations,the interlayer friction is estimated according to the Prandtl-Tomlinson model calculation method.Compared with the friction between homostructures,the friction between heterostructures is lowered by orders of magnitude,which could be attributed to its ultralow sliding potential barrier.The stick-slip instability could be observed in homostructure,while heterostructure exihibits smooth friction loops.The 2D sliding path between the layers is recorded in the sliding process,showing its dependence on both the potential energy barrier and the spring constant.The sliding path shift increases with the increase of potential energy barrier and the decrease of spring constant in the y direction.This method is also applicable to tribological systems with dominated interfacial van der Waals interaction.

atomic scale friction,Prandtl-Tomlinson model,two-dimensional materials,interlayer sliding

4 June 2017;revised manuscript received 11 July 2017)

(2017年6月4日收到;2017年7月11日收到修改稿)

10.7498/aps.66.196802

∗国家自然科学基金(批准号:51422504,51505217,51527901)资助的课题.

†通信作者.E-mail:mtb@mail.tsinghua.edu.cn

©2017中国物理学会Chinese Physical Society

PACS:68.35.Af,81.05.ue

10.7498/aps.66.196802

*Project supported by the National Natural Science Foundation of China(Grant Nos.51422504,51505217,51527901).

†Corresponding author.E-mail:mtb@mail.tsinghua.edu.cn