考虑支撑间隙的齿轮系统动力学响应分析

张 将，秦训鹏，陈浩冉

（1.武汉理工大学 汽车工程学院，武汉 430070；2.现代汽车零部件技术湖北省重点实验室，武汉 430070）

考虑支撑间隙的齿轮系统动力学响应分析

张 将1，2，秦训鹏1,2，陈浩冉1,2

（1.武汉理工大学 汽车工程学院，武汉 430070；2.现代汽车零部件技术湖北省重点实验室，武汉 430070）

以两轴式变速器三档传动齿轮为研究对象，对于通过花键与输出轴连接的从动齿轮，由于制造误差和装配误差，在其中心处所存在的支撑间隙必将影响齿轮传递动态特性，对此以二状态模型描述从动齿轮支撑处间隙副的接触状态及碰撞摩擦特性，建立考虑时变啮合刚度，齿侧间隙，综合齿频误差等非线性特性因素的运动微分方程，采用变步长Runge-Kutta法对状态方程进行数值求解，结合相图、Poincare截面和功率谱密度图，综合分析间隙值大小等因素对齿轮系统的动力学特性的影响。数值算例分析表明，随着间隙值的增大，齿轮啮合线的传递误差从单周期运动逐渐过渡到混沌运动，从动轮的位移响应经历了单周期-准周期-单周期的变化；间隙值过大时，间隙副出现明显的单边接触状态。

振动与波；齿轮系统；支撑间隙；非线性动力学；二状态法

齿轮系统是各种机器和机械装备中应用最广的动力和运动传递装置，其力学行为和工作性能对机器有重要的影响。近年来，对于齿轮传动的精度、振动和噪声等特性提出了更高的要求，并随着非线性科学的发展，国内外学者对于齿轮传动系统的非线性现象展开了大量深入的研究与分析。Theodossiadas S采用解析法对于含有轮齿间隙和时变啮合刚度的齿轮系统进行了研究，确定了齿轮系统的周期性稳态响应，并对其进行数值求解[1]；Al-Shyya等建立了单级行星轮系非线性扭转振动模型，运用增量谐波平衡法对系统的响应进行求解，并将解析解结果数值法结进行了对比[2]；Chang Jian等在含时变啮合刚度模型的基础上研究了齿轮系统中含有非线性悬挂和无非线性悬挂模型，利用分形维数和分岔图等方法分析两者的区别[3]；Parke等建立了行星齿轮传动的扭转集中参数模型和有限元模型，分析比较了两种模型下行星齿轮传动的非线性动力学响应[4]；许生等以分岔和混沌作为分析手段，研究单对齿轮传动系统在不同载荷下齿侧间隙的大小对齿轮非线性动力徐响应的影响[5]；李同杰等建立行星齿轮系扭转非线性振动模型，结合Poincare图形分析，研究转速、啮合阻尼以及齿侧间隙等参数对系统分岔特性的影响，同时利用改进后的PNF方法，研究了间隙行星齿轮非线性传动系的周期轨道及其稳定性[6–7]；王鑫等分别建立了含行星轮断齿和磨损故障的行星轮系量纲一非线性动力学方程，研究了行星轮断齿故障、行星轮全齿磨损故障随激励频率变化的分岔特性及故障特性，并分析了啮合阻尼比及外部激励对系统的影响[8]。李晟等建立了两级行星齿轮传动系统非线性扭转动力学模型，研究了激励频率、啮合阻尼比对系统分岔与混沌特性的影响[9]；巫企晶等分析了拉威娜式复合行星齿轮传动系统中激励频率对系统分岔与混沌特性的影响[10]。

以上研究多针对齿轮系统内外部激励对其动态特性的影响，其简化的模型中有一些影响因素并未完全考虑到非线性动力学模型中，如齿轮与传动轴连接副处的支撑间隙。本文针对两轴式变速器三档传动齿轮，其从动轮通过花键和输出轴相连，由于制造误差和装配误差，在从动轮中心支撑处必然存在间隙，并且对齿轮传递特性产生影响，对此应用二状态法描述从动轮与传动轴之间的间隙副接触状态，建立含有支撑间隙的单对齿动力学模型。对上述模型进行数值分析，基于非线性动力学相关理论，借助相平面、Poincare映射及分岔特性等分析了支撑间隙对齿轮系统动力学性能的影响。

1 含间隙的齿轮副动力学模型

建立一个含有时变啮合刚度、啮合阻尼、综合齿频误差、齿侧间隙以及支撑接触副间隙等多种非线性因素的动力系统，采用集中质量法建立齿轮系统非线性动力模型，即认为系统是由只有弹性而无质量的弹簧和只有质量而无弹性的质量块组成的。假设主动轮的力矩由电机直接提供，其支撑处刚度足够大；考虑从动轮处传动轴与齿轮之间的间隙，传动轴半径为R1，与传动轴配合的从动轮孔半径为R2，则接触副的间隙为r=R2-R1；齿轮之间的啮合力始终作用在啮合线方向上，由此得到简化后的含间隙单对齿轮啮合的动力学模型如图1所示。

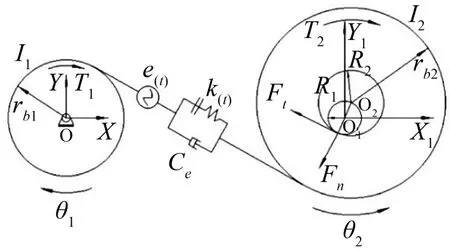
图1 含间隙单对齿轮啮合动力学模型

建立在主动轮中心处的坐标为OXY，从动轮传动轴中心处的坐标系为O1X1Y1，上述坐标均为固定坐标系，设从动轮中心O2在O1X1Y1坐标系中的位移为（x2，y2），则中心距O1O2为

当中心距小于半径间隙r时，两构件将不接触，故自由状态的条件判断条件为

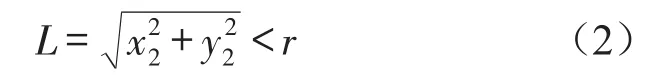
接触状态条件为

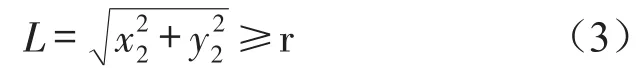
取等号表示开始接触，取“＞”表示两构件接触且接触表面有变形。

接触时的接触角φ即O1O2与X1轴的夹角为

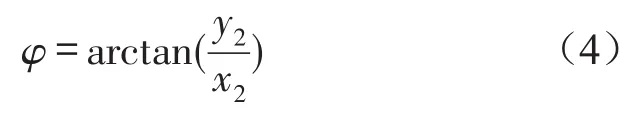
故在接触点处，运动的从动轮相对于传动轴的的法向速度和切向速度为

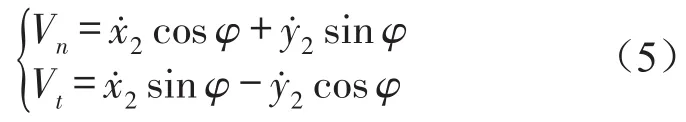
引入阶跃函数δ

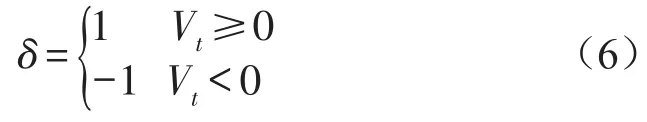
表示δ与Vt的正负号相同。引入判断函数σ

表示传动轴与孔为接触状态时，可计算出接触力，当两者为自由接触状态时，认为其接触力为零。认为构件表面具有弹性和阻尼，把接触表面力-位移特性线性化，可得接触力的法向和切向分力为

式中K，Cn，Ct，f分别为接触副元素表面的线性化接触刚度系数、线性化法向黏性阻尼系数、切向黏性阻尼系数和库仑摩擦系数。

图1中，rb1，rb2分别为主从动轮的啮合基圆半径；k(t)为齿轮副的时变啮合刚度；Ce为齿轮副的啮合阻尼系数；e(t)为综合齿频误差；T1、T2为作用在主从动轮上的转矩；θ1、θ2分别为主从动轮的扭转角位移；I1、I2为主从动轮的转动惯量。

根据模型得到系统的含间隙运动微分方程为

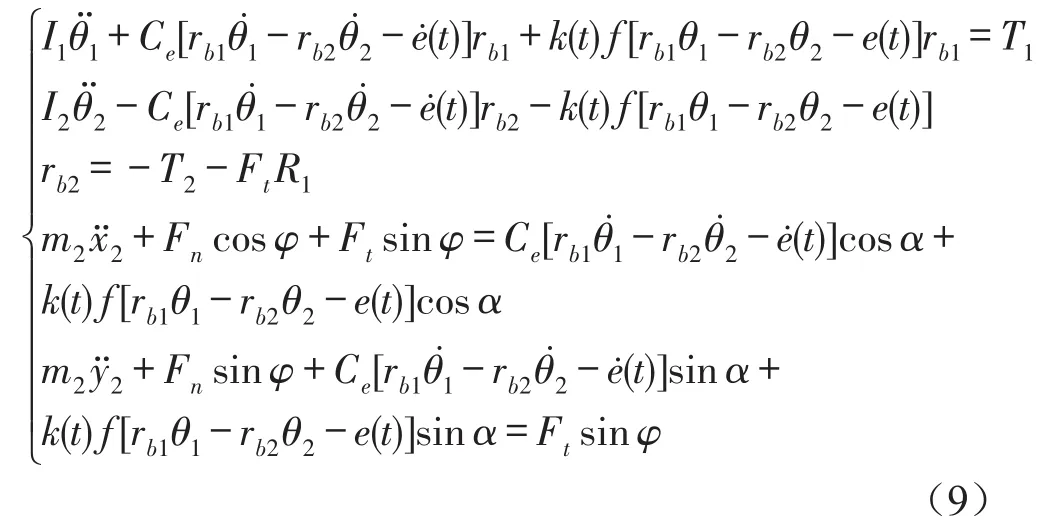
式中f是指具有侧隙时的轮齿间的啮合力非线性位移函数，具有线性分段性；若假设齿轮副间的侧隙为2b，则此分段函数f可表示为

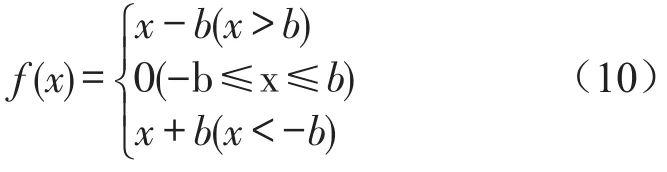
引入轮齿在啮合线上的传递误差为

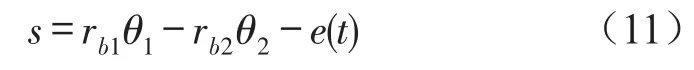
对式（9）可化简为

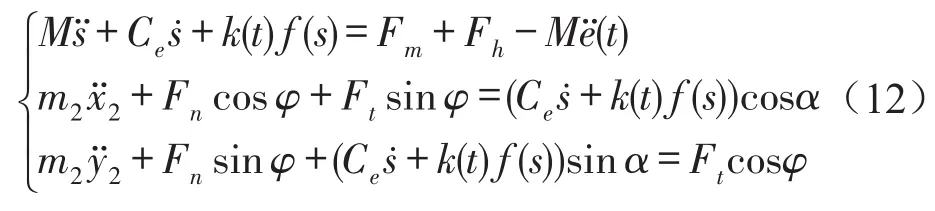
式中M为齿轮副的等效质量，为系统的外部载荷激励，为由于间隙接触副摩擦引起的载荷激励，为齿轮副的啮合角。

齿轮在啮合过程中会存在啮合刚度激励，刚度激励就是齿轮啮合过程中由综合刚度的时变性引起的动态激励。本文根据石川算法计算出各啮合齿轮的变形，进而得出单对齿啮合刚度和双对齿啮合刚度，将轮齿啮合时变刚度的变化近似为矩形方波的周期变化，通过傅里叶级数展开并略去高阶项后整理得

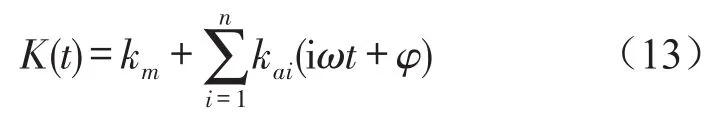
式中km为平均啮合刚度；kai为变刚度幅值，ω为轮齿啮合频率，ω=πnz/30 ，n，z，φ为转速、齿数及相位角。

齿轮的综合误差为单频的简谐函数，即

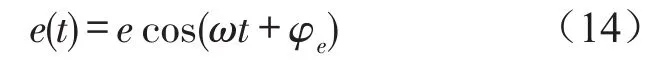
式中e为综合误差幅值，φe为对应的相位角。

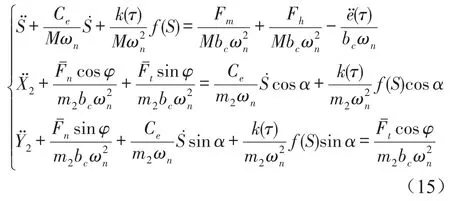
2 方程的求解及系统的稳态响应分析

对于间隙性非线性微分方程组，本文采用变步长自适应Runge-Kutta数值积分方法来得到方程的数值解，并对某变速器单对啮合齿轮进行了计算。被计算的齿轮系统参数为：齿数Z1=23，Z2=35；压力角α=20°，齿轮质量m1=1.362 kg，m2=0.566 kg；模数m=2 mm，齿频误差幅值为e=30 μm，齿侧间隙为b=80 μm，初始相位角φe=0，驱动转矩T1=90 N·m，负载转矩T2=135 N·m，啮合刚度通过石川算法计算变形后用4阶傅里叶级数拟合。

假设中间传动轴的半径为8 mm，分别计算间隙值为0 μm，10 μm，20 μm，50 μm，100 μm下系统的响应，用啮合线上的传递误差S和从动轮位移X2考察间隙值对齿轮传递系统的动态响应。

图2为间隙值为0时的分析结果，从动轮不发生任何方向上的位移，S的稳态响应为单周期运动，相图为椭圆，Poincare截面为单个离散点，FFT频谱只出现在激励频率上，此时的系统为单频激励下的单频响应。

图2 轮齿啮合线上的传递误差响应（r=0 μm）

图3、4为间隙为10 μm时的分析结果，S的稳态响应为二周期运动，Poincare截面为两个离散点，FFT频谱分别分布在两个离散频率处；X2的响应为非谐单周期响应，此时响应的时间历程也为单周期运动，相图为椭圆闭合曲线，Poincare截面为单个离散点，FFT频谱集中分布在单个离散点处。

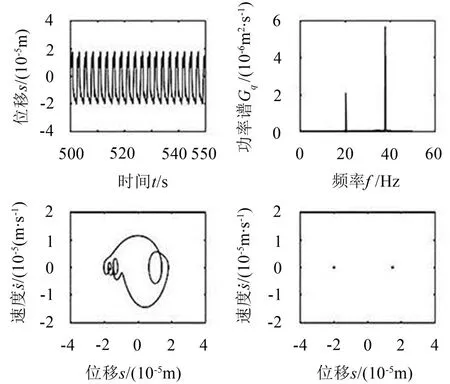
图3 轮齿啮合线上的传递误差响应（r=10 μm）

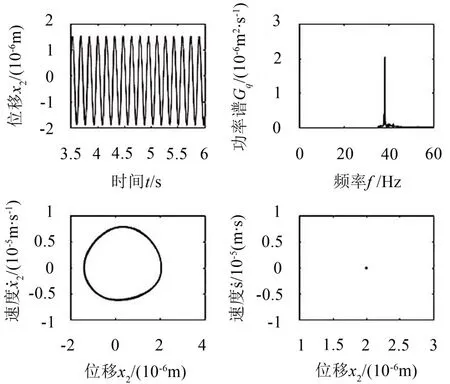
图4 从动轮的位移响应（r=10 μm）

图5、图6为间隙为20 μm时的分析结果，此时S的响应为准周期响应，在时间历程图上出现了与时变啮合刚度内激频率相关的成分，近似为周期运动；其相图为具有一定宽度的闭合曲线带，Poincare截面为多个离散点总体上趋近于封闭曲线，FFT频谱分布在两个离散点处；X2的响应依然为单周期响应，Poincare截面为单个点，FFT频谱分布集中分布在单个频率处，但是在其附近出现了离散分布的频谱。

图7、8为间隙为50 μm时的分析结果，此时S的响应为有界的非周期运动，相图为闭合的曲线带，Poincare截面为离散分布的点团，功率谱上开始出现连续谱；X2的响应为准周期响应，其时间历程近似为周期运动，相图近似为具有一定宽度的闭合曲线带，Poincare截面为集中分布的单个点团，FFT频谱总体上集中分布在单个离散点处，但附近出现连续谱。

图9、图10为间隙为100 μm的分析结果，此时S的响应逐渐变为混沌运动，其Poincare截面上的点和考虑的振动周期数一样多，FFT频谱离散的分布在多个频率处；但是X2的响应此时表现为单周期运动，相图为椭圆闭合曲线，Poincare截面为单个点。

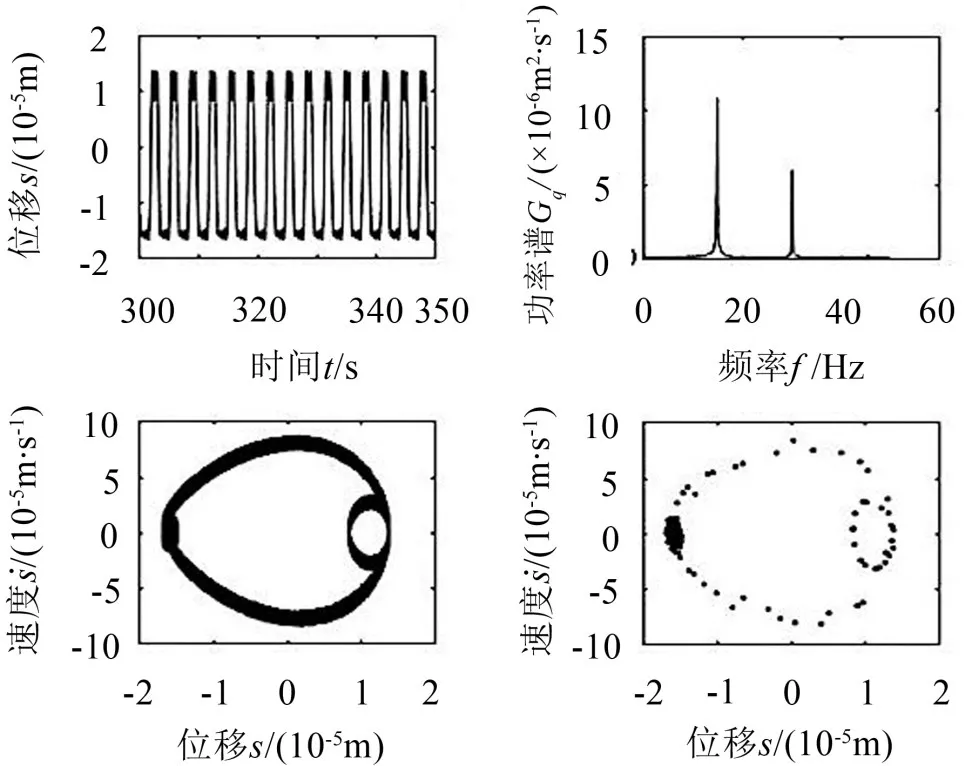
图5 轮齿啮合线上的传递误差响应（r=20 μm）

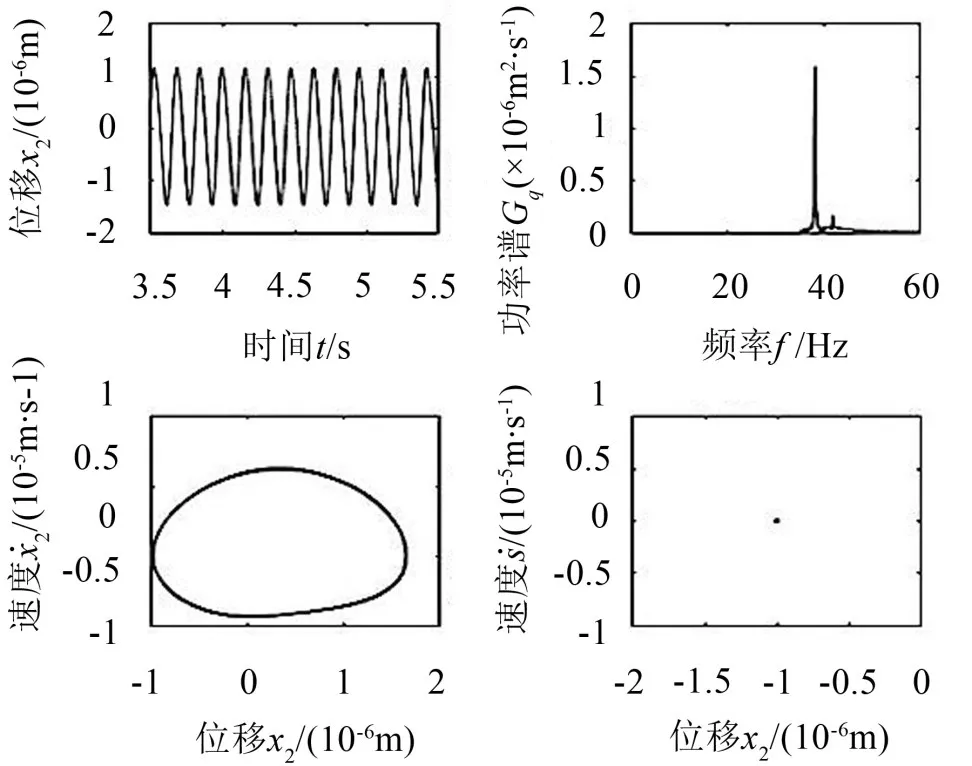
图6 从动轮的位移响应（r=20 μm）

从中可以看出，随着间隙的逐渐增大，S的响应经历了单周期运动-准周期运动-混沌运动的变化过程，X2的响应经历了单周期运动-准周期运动-单周期运动的变化过程，可以看出在间隙值较小的时候，轮齿间的啮合传递误差以及从动轮的位移响应均为单周期运动，随着间隙的增大，系统响应的非线性特征明显，传递误差响应的运动形态发生明显改变，逐渐由准周期运动过渡到混沌运动，从动轮位移响应从单周期运动过渡到准周期运动；但当间隙过大时，从动轮位移响应又变为了单周期响应，并且从图10中的时间历程图可以看出从动轮的平衡位置点从中心偏离了一定距离，约2.5 μm，此时传动轴与孔之间的接触状态表现为单边接触，即轴与孔的接触碰撞只发生在轴一侧某一部分曲面处，显然此种运动状态将会造成轴与孔的磨损加剧，局部应力增大等现象，对齿轮寿命将会造成严重的影响，故在实际设计过程中应避免间隙过大的现象发生。

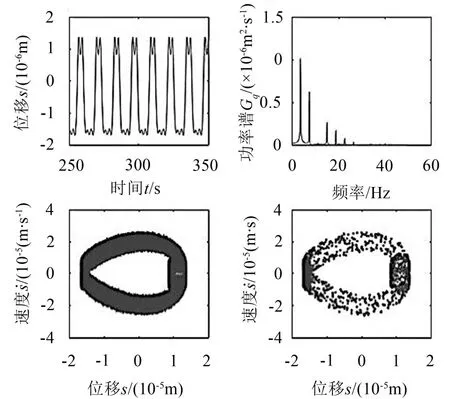
图7 轮齿啮合线上的传递误差响应（r=50 μm）

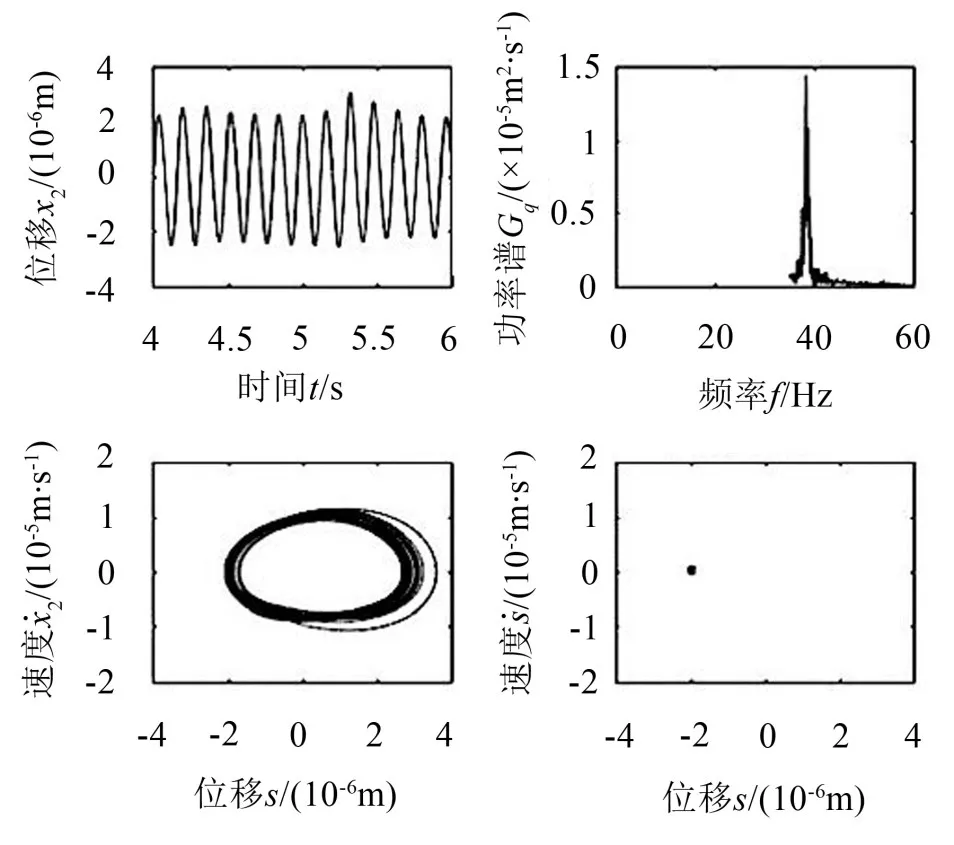
图8 从动轮的位移响应（r=50 μm）

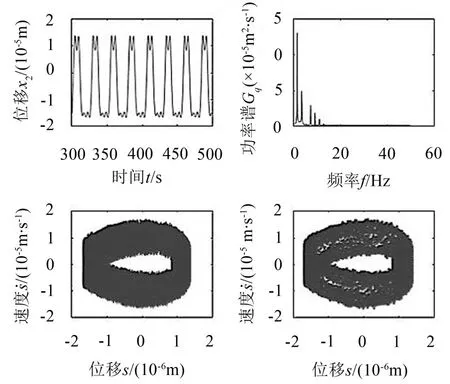
图9 轮齿啮合线上的传递误差响应（r=100 μm）

图10 从动轮的位移响应（r=100 μm）

3 结语

（1）利用二状态法描述齿轮系统支撑间隙副处的接触状态，建立了含有间隙的齿轮系统动力学模型，计入支撑间隙后系统的运动形态会发生明显改变，使得系统具有强非线性特征，且齿轮啮合线上的传递误差受间隙影响较大，因此在齿轮系统动力学分析过程中考虑支撑间隙是必要的。

（2）间隙值对啮合线上的传递误差影响显著，不考虑间隙时，其动态响应为单周期运动，随着间隙值的增大、系统响应由小间隙的准周期响应逐步过渡到混沌运动。

（3）间隙较小时，从动轮的响应为单周期运动，其平衡位置位于中心点附近，间隙值增大，其系统响应逐步过渡到准周期响应，当间隙值过大时，其响应回到单周期运动，但平衡位置偏离中心点，此时的间隙副接触状态表现为单边冲击状态，此种响应严重影响齿轮的运行状况和使用寿命，因此在实际工程中要避免间隙过大的现象。

[1]THEODOSSIADAS S,NATSIAVAS S.Nonlinear dynamics of gear-pair systems with periodic stiffness and backlash[J].Journal of Sound Vibration,2000,229(2):287-310.

[2]AL-SHYYAB A,KAHRAMAN A.A nonlinear dynamic model for planetary gear sets[J].Proceedings of the Institution of Mechanical Engineers.Part K:Journal of Multi-body Dynamics,2007(221):567-576.

[3]CHANG-JIAN C W.Strong nonlinearity analysis for gearbearing system under nonlinear suspension-bifurcation and chaos[J].Nonlinear Analysis:Real World Applications,2010,11(3):1760-1774.

[4]PARKER R G,AGASHE V,VIJAYAKAR S M,Dynamic response of a planetary gear system using a finite element contact mechanics model[J].Transactions of the ASME Journal of Mechanical Design,2000,122(3):304-310.

[5]许生，曾凡玲，张士路.含间隙的变速器齿轮系统动力学响应分析[J].农业装备与车辆，2013，51(6)：1-4.

[6]李同杰，朱如鹏，鲍和云.行星齿轮系扭转非线性振动建模与运动分岔特性研究[J].机械工程学报，2011，47(21)：76-83.

[7]李同杰，朱如鹏，鲍和云.行星齿轮传动系的周期运动及其稳定性[J].振动工程学报，2013，26(6)：815-821.

[8]王鑫，徐玉秀，武宝林.行星轮系故障状态下分岔与混沌特性分析[J].机械科学与技术，2017，36(3)：359-364.

[9]李晟，吴庆鸣，张志强.两级行星轮系分岔与混沌特性研究[J].中国机械工程，2014，25(7)：931-936.

[10]巫企晶，刘振皓，潜波，等.复合行星齿轮传动系统分岔与混沌特性研究[J].华中科技大学学报（自然科学版），2012，40(2)：9-13.

[11]石建飞，张艳龙，王丽，等.Duffing系统的双参数分岔与全局特性分析[J].噪声与振动控制，2016，36(6)：33-37.

[12]孙方旭，刘树勇，何其伟.Holmes型Duffing系统动力学特性仿真及实验[J].噪声与振动控制，2016，36(2)：17-26.

[13]程欧，苟向锋.多自由度齿轮系统非线性动力学分析[J].噪声与振动控制，2015，35(6)：31-35.

[14]杨富春，周晓军，胡宏伟.两级齿轮减速器非线性振动特性研究[J].浙江大学学报(工学版)，2009，43(7)：1243-1248.

[15]魏静，孙清朝，孙伟，等.高速机车牵引齿轮传动系统动态特性及非线性因素影响研究[J].振动与冲击，2012，31(17)：38-43.

[16]曹端超，康建设，赵劲松，等.改进EMD和HMM的齿轮故障诊断方法应用[J].噪声与振动控制，2013，33(3)；208-211.

Dynamic ResponseAnalysis of Gear Systems with Support Clearance Considered

ZHANG Jiang1,2,QIN Xun-peng1,2,CHEN Hao-ran1,2
(1.College ofAutomotive Engineering,Wuhan University of Technology,Wuhan 430070,China;2.Key Laboratory of ModernAutomobile Spare Parts Technology of Hubei Province,Wuhan 430070,China)

The third grade gear pair of the twin-shaft transmission system is taken as the research object.The driven gear and the output shaft are connected by a spline.Due to the manufacturing error and the assembly error,the support clearance in the center of the driven gear is inevitable which will affect the dynamic characteristics of the gear transmission system.In this paper,the contact state and the friction characteristics of the connection between the gear and the transmission shaft are simulated by the double-state model.The dynamic differential equations are established considering the nonlinear factors such as time-varying meshing stiffness,backlash and comprehensive tooth frequency error.The state equations are solved by the Runge-Kutta method with variable step size.With the help of the phase diagram,Poincare section and power spectrum density diagram,the influences of the clearance on the dynamic characteristics of the gear system are analyzed.Numerical results of the example show that with the increase of the clearance,the transmission error on the gear meshing line changes gradually from single periodic motion to chaotic motion,the displacement response of the driven wheel changes from single periodic motion to quasi-periodic motion and then returns to single periodic motion.The clearance pair shows an obvious unilateral contact state when the clearance value is too large.

vibration and wave;gear system;support clearance;nonlinear dynamics;double-state model

A

10.3969/j.issn.1006-1355.2017.05.011

1006-1355(2017)05-0050-05+159

2017-03-09

武汉理工大学研究生优秀学位论文培育资助项目（2016-YS-050）

张将（1993－），男，湖北省松滋县人，硕士生，主要研究方向为轮毂电机动力学与控制。

E-mai:13618646541@163.com