周期激励Ueda电路系统的双参数特性分析
2017-10-23张艳龙石建飞
张艳龙,石建飞,王 丽
(1.兰州交通大学 机电工程学院,兰州 730070; 2.兰州城市学院 数学学院,兰州 730070)
周期激励Ueda电路系统的双参数特性分析
张艳龙1,石建飞1,王 丽2
(1.兰州交通大学 机电工程学院,兰州 730070; 2.兰州城市学院 数学学院,兰州 730070)
数值计算周期激励Ueda电路系统在双参数平面上的最大Lyapunov指数,得到系统在双参数平面上周期运动、拟周期运动和混沌运动的参数区域。结合单参数分岔图和庞加莱截面图讨论多参数耦合对系统运动稳定性的影响以及系统在参数平面上的分岔混沌过程,表明在不同的参数匹配下系统的局部动力学特性非常复杂,参数之间的相互耦合关系对系统分岔与混沌过程的影响非常明显:当外激励幅值小于1.0时,系统在外激励频率小于1.181或大于1.936的区域内均为拟周期运动;当外激励幅值大于1.0时,系统在外激励频率小于0.9和大于2.5的区域内出现混沌运动和周期运动相交替的现象;选取合适的参数,系统由拟周期运动经锁相退化为周期运动,后经倍周期分岔序列进入混沌运动;在给定系统参数下,当外激励频小于0.2时,系统振子发生颤振。
振动与波;Ueda电路;多参数匹配特性;Lyapunov指数;分岔
Key kords:vibration and wave;Ueda circuit;multi-parameter matching characteristic;Lyapunov exponent;bifurcation
非线性动力学系统随系统参数变化而出现分岔和混沌是非常普遍的现象[1–3]。目前,很多学者通过计算系统在双参数平面上的分岔图,研究系统随双参数变化时的分岔特性,如文献[4]对两自由度碰撞振动系统的多参数分岔以及各参数之间的匹配规律进行了研究,得到系统在参数平面上的各种分岔曲线以及不同类型周期运动的参数区域;文献[5]对参数周期转换洛伦兹系统的双参数分岔进行了研究;文献[6]对耦合发电机系统的分岔和双参数特性进行了研究,研究发现不同控制参数对系统动力学行为的影响特性有所差异;文献[7–9]对多参数非常规分岔以及多参数分岔的分形结构进行了一定的研究;文献[10]利用PNF和分岔延续算法相结合的方法研究了行星齿轮传动系统在一组给定参数下共存的周期运动,并判断了各共存周期运动的稳定性;文献[11]根据特征值理论研究了Laser系统在双参数条件下的分岔特性。对于系统在双参数平面上最大Lyapunov指数的计算与分析却鲜有文献报道。
周期激励Ueda电路是一个高度非线性的动态系统[12],它既具有Duffing方程中的非线性能量存储项,又具有Van der Pol方程中的非线性阻尼项。文献[13]研究了周期激励Ueda电路中的Hopf分岔,基于Hopf分岔条件给出了一个确定混沌参数区域的方法。而对周期激励Ueda电路系统多参数匹配特性的研究却很少见有文献报道,系统在运动过程中不可能只受单参数的影响,为了得到系统在参数大范围内变化时的动力学特性,有必要对系统的多参数耦合特性进行研究。
本文针对周期激励Ueda电路系统,通过数值计算系统在参数平面ω-f上最大Lyapunov指数(the Top Lyapunov Exponent,简称TLE)来研究参数匹配对系统动力学特性的影响,结合系统单参数分岔图、庞加莱截面图对系统在双参数平面上TLE的分布进行分析和验证。最后研究参数μ对系统在参数平面ω-f上TLE分布的影响。
1 系统在双参数平面上TLE的分布
无量纲化后,周期激励Ueda振荡电路[12]描述为

式中μ是系统参数,f和ω分别是外加周期激励信号的幅度和频率。
数值仿真f=0.2、0.6、1.0、1.5、2.0、3.0、4.0变化时参数平面ω-f上最大Lyapunov指数的变化区域。由于篇幅限制仅以μ=0.2时为例,结合单参数分岔图和庞加莱截面图讨论了多参数耦合对系统运动稳定性的影响以及系统在参数平面上的分岔混沌过程。图1为周期激励Ueda振荡电路系统在μ=0.2时参数平面ω-f上TLE的分布图,其中深灰色区域为系统TLE近似等于0的拟周期运动区域;黑色区域为系统TLE大于0的混沌运动;浅灰色区域为系统TLE小于0的稳定周期运动。
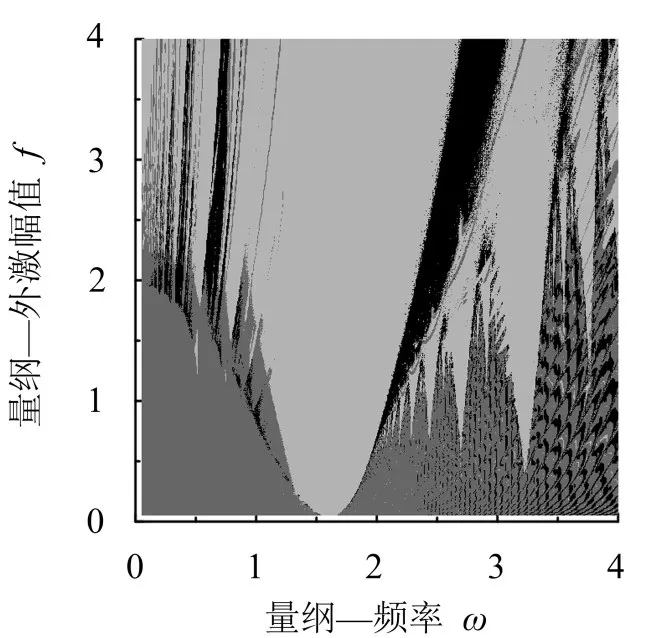
图1 系统在参数平面上TLE的分布图,μ=0.2
图中ω在1.5附近时,随f的增加,存在浅灰色周期区域,且该周期区域面积不断向两边扩展;当f较小时(图1底部),在左下部和右下部均为深灰色拟周期运动区域,当ω较大时右下部深灰色区域内系统出现了较小鱼鳞状的黑色区域,系统在该区域内仍为拟周期运动,其TLE在0附近的扰动范围有所增大;当f较大,系统在ω较小和较大时(图1左上部和右上部)均出现黑色混沌带,在该区域内系统出现混沌运动和周期运动相交替的现象,动力学特性很复杂。
2 系统在双参数平面上的分岔过程
取μ=0.2,f=0.5计算系统随ω变化的单参数分岔图和相应TLE图分别如图2(a)和图2(b)所示,在图2(b)中当ω∈[1.181,1.936]时系统TLE明显小于0,系统在该参数区间内表现为稳定周期运动,当ω<1.181或ω>1.936时其TLE在0附近上下扰动,而且当ω>1.936时,随着ω的增大其扰动幅度也越来越大,表明系统不稳定性越来越强。图2(c)为ω=2.0时的庞加莱截面图,表现为1个闭合的极限环,表明系统为拟周期运动,对应图2(b)其TLE=-0.000 8。
取μ=0.2,f=1.5计算系统随ω变化的单参数分岔图和相应TLE,如图3(a)和图3(b)所示,图3(a)中随ω的变化系统出现了多条宽度不同的黑色带,对比图3(a)和图3(b)发现,ω在0.82和2.25附近的黑色带所对应的TLE明显大于0,表明系统在该黑色带内表现为混沌运动;而其它黑色带所对应的TLE近似等于0,表明系统在该黑色带内为拟周期运动。图3(c)为图3(a)在ω∈[0.65,0.90]时的放大图,系统在此区间内出现了周期运动和混沌运动或拟周期运动相交替的现象(后面详细分析)。图3(a)中,当ω∈(0.9,2.2)时系统为稳定的周期1运动,当ω=2.21时系统经鞍结分岔转迁为混沌运动,随着ω增加系统经逆倍化分岔序列退化为周期3运动。图3(d)为图3(a)在ω∈[2.52,2.62]的放大图,当ω=2.538 9时系统由周期3运动转迁为周期11运动,后由周期11运动进入拟周期运动,随着ω继续增加系统由拟周期运动退化为较短暂的周期8运动,当ω=2.606 6时系统由周期8跳跃为周期5运动,ω再增加系统由周期5运动进入拟周期运动,随后出现了周期2窗口,然后由周期2运动再次进入拟周期运动。

图3 系统分岔图和TLE谱图

图4 与图3 (c)对应的系统庞加莱截面图
下面结合Poncaré截面图对图3(c)吸引子的转迁过程进行详细分析。随ω的增加,系统由拟周期运动(如图4(a))退化为周期4运动(如图4(b)、图4(c)),后经较短暂的倍化分岔序列进入混沌运动(如图4(d));随ω的继续增加,系统混沌运动退化为周期5运动(如图4(e)),随后系统由周期5运动转迁为稳定的周期1运动,当ω=0.791时系统进入极短暂的混沌运动,随后退化为周期9运动(如图4(f));ω再增加,系统由周期9运动转迁为混沌运动(如图4(g)),随后混沌运动退化为周期7运动(如图4(h));当ω=0.848时系统出现了周期17运动,后经极短暂的混沌运动退化为周期1运动。图3(d)所示的转迁过程与图3(c)类似,限于篇幅本文没有给出Poncaré截面图。
由此可见,在参数平面ω-f上,当f=1.5,ω∈[0.848,2.251]时系统为稳定的周期1运动,当ω<0.848或ω>2.251时出现了周期运动和周期运动、周期运动和混沌运动、周期运动和拟周期运动相交替的现象。
取μ=0.2,f=3.0计算系统随ω变化的单参数分岔图和相应TLE如图5(a)和图5(b)所示。当ω较小时(ω<1.0)系统出现周期运动和混沌运动交替现象。图5(c)为图5(a)在ω∈[0.05,0.25]时的放大图,取ω的值分别为0.06、0.1和0.15计算系统相图和相应时间历程图,如图6所示。结合图5(c)和图6可以看出,当ω<0.2时Ueda振荡电路存在颤振运动,而且随ω的增加颤震逐渐减弱。图5(a)中,当ω=2.503时系统进入混沌运动,随ω增加系统由混沌运动经逆倍化分岔序列退化为周期2运动,随ω继续增加,系统由周期2进入极短暂的混沌运动,随后又退化为周期7运动,此后系统在频率ω较窄区间内出现了高周期运动与混沌运动相交替的现象,如图5(d)所示(图 5(d)为图 5(a)在ω∈[3.8,4.0]时的放大图)。

图5 系统分岔图和最大Lyapunov指数以及局部放大分岔图

图6 系统相图和对应时间历程图
由此可见,当f较大时,系统在ω=1.5附近为稳定的周期1运动,当ω较大或较小时系统的局部动力学特性变得很复杂。当ω<0.2时系统具有一定的颤震性,这种颤震性随ω的增加而减弱,系统颤震出现在低频率和高幅值情况下,这种现象在以前Ueda电路的研究中鲜有遇见。
3 参数μ对系统双参数特性的影响
取μ的值分别为0.6、1.5、2.0和4.0,数值计算周期激励Ueda振荡电路系统在参数平面ω-f上TLE分布,如图7所示,对比图1发现随参数μ的增加,图中左边区域内的黑色混沌带和分岔曲线以及深灰色区域面积不断缩小并向下移动,使得系统在参数平面上混沌运动和拟周期运动的参数范围越来越小,而稳定周期运动的参数范围不断扩大(图7(a)-图7(d)左边区域);图中当ω较小时(ω<1.5),系统在左上部表现为稳定周期运动,在左下部为拟周期运动,而在中间系统出现周期运动和混沌运动相交替的现象。当ω较大时(ω>1.5),如图7右边区域,对比图1,黑色混沌带和深灰色拟周期区域不断被浅灰色周期运动所侵蚀,表明当ω较大时,随μ增加系统稳定周期运动的参数范围在扩大,而拟周期运动和混沌运动的参数范围在缩小,而且在深灰色区域内出现了许多黑色的离散点,表明系统在该区域内TLE在不断增加,但系统仍为拟周期运动。
由此可见,在参数平面ω-f上,当外激励幅值f较小时,系统在ω变化的大部分范围内表现为拟周期运动,随μ增加,该拟周期区域面积有所减小;当f较大、ω较小时系统表现为稳定的周期运动,该周期运动区域面积随μ的增加而不断扩大;当f较大、ω较大时系统出现周期运动和混沌运动相交替的现象,随μ增加,浅灰色周期区域的面积不断增大,而黑色混沌区域和深灰色拟周期区域的面积在不断缩小,系统在该区域的稳定性开始增强。

图7 不同参数μ下系统在参数平面上的TLE分布
4 结语
本文数值计算了典型周期激励Ueda振荡电路在参数平面ω-f上的TLE,得到系统在双参数平面上不同运动形态的参数区域,结合系统单参数分岔图和相应的TLE以及庞加莱截面图,对系统各参数之间的匹配特性进行了分析,更为全面地反映了系统运动稳定性与各参数之间的关系。
随着μ的增加,在整个参数平面上系统稳定周期运动的参数区域不断扩大,而混沌运动和拟周期运动的参数区域不断缩小。当μ较小,且ω在1.5附近较小区间内取值时,系统在整个f参数范围内为稳定的周期运动;当f较小时,系统在ω较大和较小区域内为拟周期运动;当f较大时,系统在ω较大和较小区域内出现周期运动和混沌运动相交替的现象,系统在该区域的局部分岔特性非常复杂。
在一定参数条件下,系统会发生颤振运动,系统也会出现由拟周期运动经锁相、倍化分岔向混沌运动转迁的特殊过程,当系统处于拟周期运动时,其相应最大Lyapunov指数在零附近较小范围内扰动。利用系统在参数平面上最大TLE的分布图来研究非线性系统具有一定的有效性和可行性,以上研究对多参数系统在较宽条件下的非线性动力学行为研究及混沌控制具有参考价值。
[1]SHAW S W,HOLMES P J.A periodically forced piecewise linear oscillator[J].Journal of Sound and Vibration,1983,90(1):129-155.
[2]夏南,孟光.非线性系统周期强迫不平衡响应的稳定性分析[J].力学学报,2001,33(1):128-133.
[3]NORDMARK A B.Non-periodic motion caused by grazing incidence in an impact oscillator[J].Journal of Sound and Vibration,1991,145(2):279-297.
[4]LUO G W,LV X H,SHI Y Q.Vibro-impact dynamics of a two-degree-of freedom periodically-forced system with a clearance:Diversity and parameter matching of periodicimpact motions[J].International Journal of Non-linear Mechanics,2014,65:173-195.
[5]ZHANG CHUN,BI QINSHENG.On two-parameter bifurcation analysis of the periodic parameter-switching Lorenz oscillator[J].Nonlinear Dynamics,2015,81(1-2):577-583.
[6]吴淑花,孙毅,郝建红,等.耦合发电机系统的分岔和双参数特性[J].物理学报,2011,60(1):84-92.
[7]秦朝红.非线性动力学双参量奇异性方法及其工程应用[D].哈尔滨:哈尔滨工业大学,2010.
[8]PHANIKRISHNATHOTA,BERNDKRAUSKOPF.Multi-parameter bifurcation study of shimmy oscillations in a dual-wheel aircraft nose landing gear[J].Nonlinear Dynamics,2012,70(2):1675-1688.
[9]杨娟,卞保明,彭刚,等.随机信号双参数脉冲模型的分形特征[J].物理学报,2011,60(1):93-98.
[10]李同杰,朱如鹏,鲍和云,等.行星齿轮传动系统的周期运动及其稳定性[J].振动工程学报,2013,26(6):815-822.
[11]P PEPLOWSKI,H HAKEN.Bifurcation with two parameters in two- dimensional complex space applications to laser system[J].Physica.Section D,1988,30:135-150.
[12]UEDA Y,AKAMATSU N.Chaoticallytransitional phenomena in the forced negative resistance oscillator[J].Circuits and Systems,1981,28(3):217-224.
[13]南明凯,王时,朱志文,等.周期激励Ueda电路中Hopf分岔与混沌的参数区域[J].南京航空航天大学学报,1999,30(1):72-78.
Double-parameter CharacteristicsAnalysis of Ueda Circuit Systems with Periodic Excitation
ZHANG Yan-long1,SHI Jian-fei1,WANG Li2
(1.School of Mechanical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China;2.School of Mathematics,Lanzhou City University,Lanzhou 730070,China)
The top Lyapunov exponent of the Ueda circuit system with periodic excitation on the double-parameter plane is calculated,and the parameter regions of periodic motion,quasi-periodic motion and chaotic motion of the system are obtained.With the single-parameter bifurcation diagrams and Poincaré section maps,the influence of multi-parameter coupling on the system motion stability is discussed,and the bifurcation and chaos processes of the system on the doubleparameter plane are also studied.The results show that the system local dynamic characteristics are very complex under different parameters coupling.The influence of the mutual coupling among the parameters on the process of bifurcation and chaos of the system is very obvious.When the external excitation amplitude is less than 1.0,the system exhibits quasiperiodic motion in the region where the external excitation frequency is less than 1.181 or greater than 1.936.When the external excitation amplitude is greater than 1.0,the system exhibits periodic motion and chaotic motion alternatively in the range of the external excitation frequency below 0.9 or above 2.5.When the system parameters are selected appropriately,the system motion will evolve into periodic motion from the quasi-periodic motion through phase lock,and then get into chaotic motion through multi-periodic bifurcation.Under the given system parameters,the system oscillator shows chatter motion when the external excitation frequency is less than 0.2.
O322;O241
A
10.3969/j.issn.1006-1355.2017.05.007
1006-1355(2017)05-0033-05+45
2016-11-08
国家自然科学基金资助项目(11302092)
张艳龙(1981-),男,河北省围场县人,副教授,博士生,主要研究方向为动力学与控制。
E-mail:zhangyl@mail.lzjtu.cn
