FFT的数据并行计算方法研究

杨 琳，钟 升，张家田

(1.西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065；2.西安微电子研究所，陕西 西安 710065)

FFT的数据并行计算方法研究

杨 琳1，钟 升2，张家田1

(1.西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065；2.西安微电子研究所，陕西 西安 710065)

为满足G(Gigabytes)级像素帧的实时性处理需求，针对信号处理系统中处理计算量大、实时性要求高的特点，剖析了解算过程内在的数据并行特性，深入研究了基于计算阵列的谱图解算数据并行算法。提出了一种基于MPP(Massively Parallel Processor)计算机SIMD PE阵列的FFT的数据并行计算实现方法。首先根据FFT架构中的数据交互一致性，给出了数据并行计算的表达式。提出一种基于PE标识，进行条件操作的SIMD PE阵列数据并行实现方法。该方法不但省去了并行处理中的数据寻址时间开销，而且使得数据并行操作更为规则、简洁，满足了阵列操作规则性强的处理要求，大幅度地提高了MPP计算机并行计算处理速度。该方案是一种简洁有效的PE自治问题解决方案，以更合理的方法和更高的效率实现了常规经典算法，在数据并行计算领域中，无疑具有重要的理论意义和应用价值，将在嵌入式信号处理中发挥愈来愈重要的作用。

快速傅里叶变换;SIMD PE阵列;映射语言；MPP计算机

0 引 言

在数字图像变换处理中，DFT(Discrete Fourier Transform)是重要的变换算法，被广泛地用于图像匹配、纹理分析、去噪滤波等图像处理领域。FFT是采用蝶式交换的处理方式，实现了DFT变换的快速算法。针对G级像素帧的FFT处理，由于具有较高的实时性要求，使得基于MPP计算机处理阵列的数据并行实现方式成为研究热点[1-4]。在并行处理计算机上如何结合体系结构高效率地实现典型算法是并行计算的核心技术[5-10]。基于阵列的数据并行实现就是针对确定的并行算法，基于数据在阵列中的位置分布特性，拟定合适的并行计算处理步骤。在各个并行步骤已确定的前提下，各个并行步中，被操作数在阵列中的存储位置、传送距离及处理方式也是确定、已知的。对各并行步中存储被操作数PE单元进行事先标识，并将标识码预置于相应PE的PSR寄存器[11-14]，使得基于PE标识的数据并行操作，不但具有了PE“自治”(automations)能力，而且省去了数据寻址时间。各并行步的数据处理是规范，符合算法的阵列实现特点，能够很好地满足MPP计算机处理阵列操作规则性强的要求。

1 FFT的数据并行计算

FFT是采用多次蝶式变换和位序反转来实现DFT变换的快速计算方法[1-4]。为了方便起见，首先给出8点的FFT蝶式变换架构和相应的数据并行计算公式，此基础上再给出N点的FFT蝶式变换的数据并行计算公式。

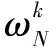
图1 8点的FFT蝶式计算架构

从图1可直观看出，各次蝶式变换中的数据交互和相应的计算处理是规则的，采用不同基色(带填充色的点和无填充色)的点来标识，在各次蝶式变换中的数据交互总是发生在以相同间隔分布的两类基色点间，且无填充色的点只进行“+”运算，填充色点进行“-”和与变换系数的乘法运算。两类代表不同操作数据类型的填充色原点的分布以及它们间的间隔距离，在每次蝶式解算中均呈现显著规律，数据并行操作便是基于这些规律来实现的。为便于描述，基于不同的运算操作来标识不同的数据类型，参照提升小波变换的命名方式，简称为数据分裂步，将具体的数据传送和计算操作称为数据计算步。这样一来，8点的蝶式变换就划分为分裂1、分裂2和分裂3以及计算步1、计算步2和计算步3。式(1)～(9)采用向量操作方式，给出对应于分裂步和数据计算步的并行计算公式。

分裂步1:

A0:={a(0),a(1),a(2),a(3)};B0:={a(4),a(5),a(6),a(7)}

(1)

计算步1:

A1:={s1(0),s1(1),s1(2),s1(3)}=A0+B0

(2)

(3)

分裂步2:

(4)

计算步2:

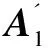
(5)

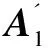
(6)

分裂步3:

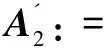
(7)

计算步3:

(8)

(9)

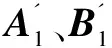
表1 N点FFT蝶式变换对应的分裂步与计算步的数据并行计算公式

至此，FFT蝶式变换的数据并行计算，就由L个分裂步和L个计算步给出。下面将主要讨论如何在SIMD PE阵列上实现FFT蝶式变换。基于SIMD PE阵列的蝶式变换数据并行实现，就是在SIMD PE阵列中实现L个分裂步和L个计算步。

2 基于SIMD PE阵列的FFT蝶式变换的数据并行实现方法

为简化起见，对8个通道以信号长度均为8的信号并行进行FFT蝶式变换为典型示例，揭示FFT变换是如何在特定处理元阵列中实现数据级并行处理的。假定处理元阵列的大小与待处理数据的规模一致，即也为8×8，且数据编号与阵列位置一致，即Signal[i][j]是放在PE阵列的处理元PE[i][j]中。阵列中各PE单元之间的互连关系采用mesh结构，如图2所示，PE间仅具备相邻通信能力。

对多个通道进行FFT蝶式变换，可看成是对一幅二维信号图进行FFT变换。在SIMD PE阵列上，就是对存放像素值的所有PE，按行方向对各PE中的像素值进行数据并行计算，计算后的结果依然存入相应的PE单元中。至此，一幅经FFT变换后的谱上的图像就存放于PE阵列中。以下先以在8×8的PE阵列中对所有的行同步执行8点FFT蝶式变换为例，具体说明FFT变换在SIMD PE阵列中的数据并行实现方法，对所有列的处理同理。在此基础上给出N点FFT蝶式变换的SIMD PE阵列实现方法。

图2 SIMD PE阵列体系结构(LS-MPP)

在SIMD PE阵列中，指令执行将结合PE单元具体的坐标位置进行相应的条件操作。由于各个计算步中各个分量的序号是与像素值无关的，是依据表1所给各个分裂步事先确定的，或者说，可以在执行计算操作前就可以确定。因此，不采用求解坐标位置的办法，而是利用各个PE单元内的Program Status Register (PSR)，即程序状态寄存器，并利用PSR中相应的状态位来提前标识各个分裂步的结果，或者说执行分裂步的工作。在8×8的PE阵列中的各个PE的PSR状态位中相应bit位将按如下原则设置：对于列坐标j=0,1,2,3的PE单元，其PSR寄存器的b0位置为0，其他PE单元内PSR寄存器的b0位设置为1；对于列坐标j=0,1,4,5的PE单元，其PSR寄存器的b1位设置为0，其他PE单元内PSR寄存器的b1位设置为1；对于列坐标j=0,2,4,6的PE单元，其PSR寄存器的b2位设置为0，其他PE单元内PSR寄存器的b2位设置为1。这样一来就可通过判别PSR的状态位来确定各个计算步中相应向量的各个分裂，或执行指定运算操作的各个PE[i,j]单元，该方法使得后续的阵列操作简洁、规则，而且没有了寻址时间开销。此外，FFT变换系数依据表1中的计算公式确定并作为立即数被提前预置于对应位置的PE内的立即数寄存器中。在SIMD PE阵列中，各个计算步的并行实现，就是基于各个PSR设置，按表1给定的计算公式，在阵列中执行相应的条件传送与条件计算操作。各个计算步的并行执行是以状态位为条件，采用映射语言M(Mapping language/Middle language)[12]的条件传送语句与条件算术语句等描述的。

//在数据加载阶段，初始数据A0与B0已加载至各PE单元的DATA_registeR0寄存器中，变换系数加载于相应PE单元的立即数寄存器LITERAL_register_1与LITERAL_registe_2中，DATA_registeR1

//在计算阶段计算步1的并行实现

1 If DATA_registeR1=(b0= =0)? DATA_registeR0[j+4]:NOP;//PE[j]←PE[j+4]；

2 If DATA_registeR1=(b0= =1)? DATA_registeR0[j-4]:NOP;//PE[j]←PE[j-4]；

3 If DATA_registeR0=(b0= =0)? {DATA_registeR0+DATA_registeR1}:NOP;

4 If DATA_registeR0=(b0= =1)? {DATA_registeR1-DATA_registeR0}:NOP;

5 If DATA_registeR0=(b0= =1)? {DATA_registeR0×LITERAL_register_1}:NOP;

//在计算阶段计算步2的并行实现

1 If DATA_registeR1=(b0= =0)? DATA_registeR0[j+2]:NOP;//PE[j]←PE[j+2]；

2 If DATA_registeR1=(b0= =1)? DATA_registeR0[j-2]:NOP;//PE[j]←PE[j-2]；

3 If DATA_registeR0=(b0= =0)? {DATA_registeR0+DATA_registeR1}:NOP;

4 If DATA_registeR0=(b0= =1)? {DATA_registeR1-DATA_registeR0}:NOP;

5 If DATA_registeR0=(b0= =1)? {DATA_registeR0×LITERAL_register_2}:NOP;

//在计算阶段计算步3的并行实现

1 If DATA_registeR1=(b0= =0)? DATA_registeR0[j+1]:NOP;//PE[j]←PE[j+1]；

2 If DATA_registeR1=(b0= =1)? DATA_registeR0[j-1]:NOP;//PE[j]←PE[j-1]；

3 If DATA_registeR0=(b0= =0)? {DATA_registeR0+DATA_registeR1}:NOP;

4 If DATA_registeR0=(b0= =1)? {DATA_registeR1-DATA_registeR0}:NOP;

对应于IDFT的IFFT蝶式处理算法，由于各处理阶段中的待处理数据在阵列中的分布位置，传送距离及处理方式与FFT基本一致，唯一不同的仅仅是各计算步中的变换系数而已，所以仅需将FFT中各计算步的变换系数更换为其倒数即可。例如，将ωk更换为ω-k，并存储于相同的PE单元中。其他设置及处理均与FFT一致，在此不再赘述。

3 性能分析与仿真验证

在运算量确定的情况下，PE间的通信开销成为衡量性能的主要指标。以下针对上述实现方法，对计算量和通信量进行讨论。对于FFT变换，计算量主要取决于算法实现中的乘、加次数和判别运算的次数。通信量主要取决于蝶式运算和位序倒置变换中的数据交互次数，表2给出了相关的统计值。

表2 FFT的计算量及通信次数

在FFT变换运算中，涉及大量的复数加法和乘法运算。1次复数加法由2次实数加法构成，1次复数乘法由4次实数乘法和2次实数加法构成。以N=64×64点的FFT计算为例，在单处理器环境下，完成蝶式变换，共需64×(64×6)次复数加法和64×(32×5)次复数乘法；完成位序倒置，共需64×56次数据交换操作。为简化起见，约定实数的加法和乘法运算、位判别运算以及PE单元间的相邻通信均可在一个指令周期内完成，并且访存时间也为2个指令执行周期。则对于单处理器而言，按上述约定，大约需要372 736个指令周期。对于文中方案，由表2可简单地计算出共需634个指令周期。其加速比约为587.92，很可观。文中采用的仿真软件为Parallaxis-Ⅲ，完成PE阵列的规模和互联结构的定义，其中PE间的数据交互是使用系统函数MOVE模拟实现。

如图3所示，通过仿真验证了实现方法的正确性。

图3 2D-FFT变换仿真图像

4 结束语

针对G级像帧实时处理的需要，研究了FFT在MPP计算机处理SIMD PE阵列上的数据并行计算实现方法。该方法的并行度不受算法限制，而且省去了寻址计算量和寻址时间，各个并行操作步骤规则、简洁且通用性强。该方法亦可应用于其他算法的并行实现[12-14]。

从硬件上讲，并行度仅受PE阵列规模的限制。由于SIMD PE阵列具有较强的可剪裁性，其大小是容易随应用的并行性要求而变化的；特别是随着芯片集成度的提高，阵列规模急速上升，容易满足大规模数据的处理需求。

[1] Tong C,Swartztrauber P N.Ordered fast Fourier transform on an massively parallel hyper cube multiprocessor[J].Journal of Parallel and Distribute Computing,1991,12(1):50-59.

[2] Swartztrauber P N.Multiprocessor FFTs[J].Parallel Computing,1987,5(1-2):197-210.

[3] Jamieson L H,Muller L P,Siegal H.FFT algorithm for SIMD parallel processing system[J].Journal of Parallel and Distributed Computing,1986,3(1):48-71.

[4] Berland G D,Wilson D.A fast Fourier transform algorithm for a global,highly parallel processor[J].IEEE Transactions on Audio and Electroacoustics,1969,17(2):125-127.

[5] Khailany B,Dally W J,Kapasi U J,et al.Imagine:media processing with streams[J].IEEE Micro,2001,21(2):35-46.

[6] Rixner S. Stream processor architecture[M].Boston,MA:Kluwer Academic Publishers,2002.

[7] Kapasi U J.The imagine stream processor[C]//Proceedings of IEEE 2002 international conference on computer design.[s.l.]:IEEE,2002:282-288.

[8] Serebrin B.A stream processor development platform[C]//Proceedings of IEEE 2002 international conference on computer design.[s.l.]:IEEE,2002:303-308.

[9] Crowley P. Network processor design issues and practices[M].[s.l.]:Morgan Kaufmann Publishers,2003.

[10] 陈国良.并行算法的设计与分析[M].北京：高等教育出版社，2002:380-409.

[11] 沈绪榜,刘泽响,王 茹.计算机体系结构的统一模型[J].计算机学报，2007，30(5)：729-736.

[12] 钟 升,沈绪榜,郑江滨,等.提升小波变换的数据并行计算方法研究[J].计算机学报,2011,34(7):1323-1331.

[13] 钟 升.基于SIMD PE阵列的DCT数据并行实现方法研究[J].电子学报,2009,37(7):1546-1553.

[14] 钟 升.基于小波变换的图像bit纠错数据并行实现研究[J].系统仿真学报,2008,20(8):2137-2141.

ResearchonDataParallelComputationMethodofFFT

YANG Lin1，ZHONG Sheng2，ZHANG Jia-tian1

(1.Key Laboratory of Photo-electricity Gas-oil Logging and Detecting of Ministry of Education, Xi’an Shiyou University,Xi’an 710065,China; 2.Xi’an Microelectronic Technique Institute,Xi’an 710065,China)

In order to satisfy the real-time processing requirement of G-level pixel frame,considering the intensive and real time computing requirement of signal processing in embedded signal system,the inner data parallelism of the calculation process is analyzed,and the data parallel algorithms of spectrogram calculation based on computing array is also researched.A data parallel computation method implemented on SIMD PE array of MPP (Massively Parallel Processor) computer for FFT transform is presented.Based on the data computing consistency of FFT,the expression of data parallel computing is given firstly.Then a method of data parallel computing based on SIMD PE array to execute conditional operations by using of PE identifier is proposed,which not only omits the time cost of addressing,but makes the data parallel operation more regular and compact (only in computation statements and move statements).It meets the features of high regularity required by SIMD and greatly improves MPP computer processing speed,which is also a simple and effective PE autonomy solution,realizing conventional classic algorithms with more rational method and higher efficiency.It has important theoretical significance and application value in the area of data parallel undoubtedly,which will play a more and more important role in embedded signal processing.

FFT;SIMD PE array;mapping language；MPP computer

TP301

A

1673-629X(2017)10-0091-05

2016-10-27

2017-02-14 < class="emphasis_bold">网络出版时间

时间：2017-07-19

陕西省科技统筹创新工程计划(2015KTTSGY04-05)

杨 琳(1982-)，女，硕士研究生，研究方向为电子与通信工程；钟 升，研究员，研究方向为计算机体系结构、信号处理、微工艺系统；张家田，教授，研究方向为通信工程与信号处理。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170719.1109.028.html

10.3969/j.issn.1673-629X.2017.10.020