升力来自于流体的膨胀与压缩

摘要：本文提出了升力来自于流体的膨胀与压缩的理论，间接地批判了用伯努利定律解释升力的理论。

关键词：流体力学；升力；膨胀；压缩；伯努利定律；机翼；飞机设计

一般人们都用伯努利定律解释升力现象，本文提出一种新的升力理论，这种理论认为，升力来自于流体的膨胀与压缩。

让我们由一个实验开始：

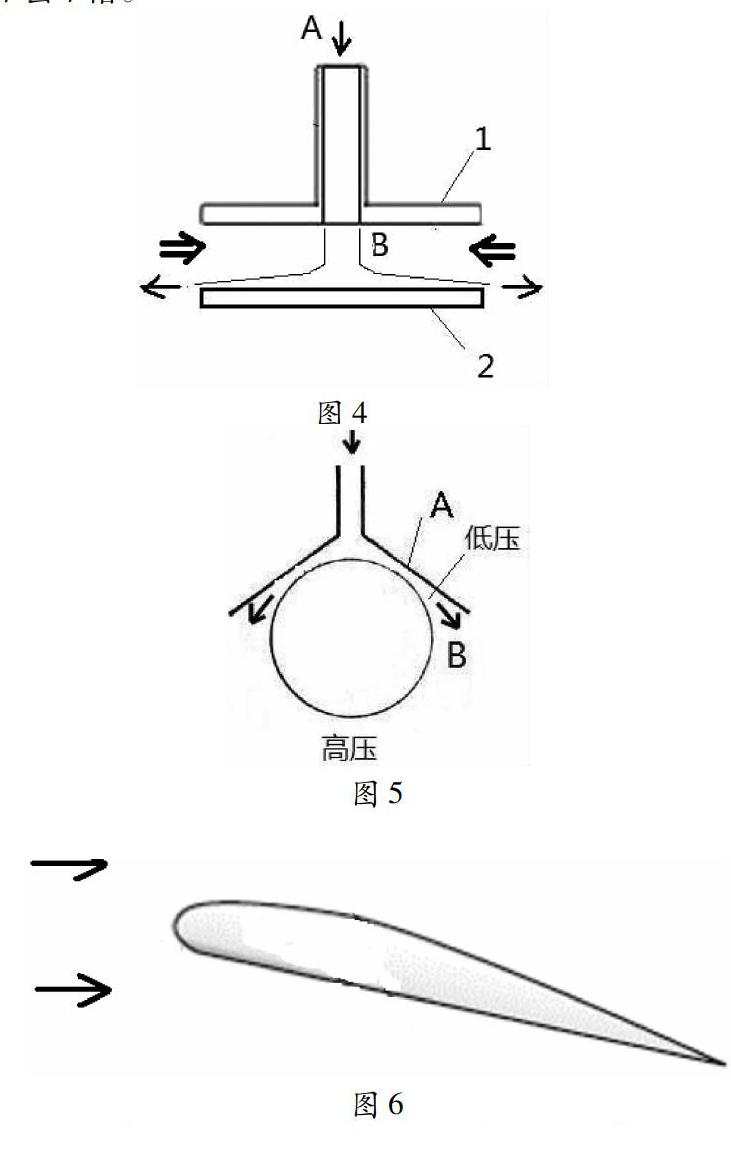
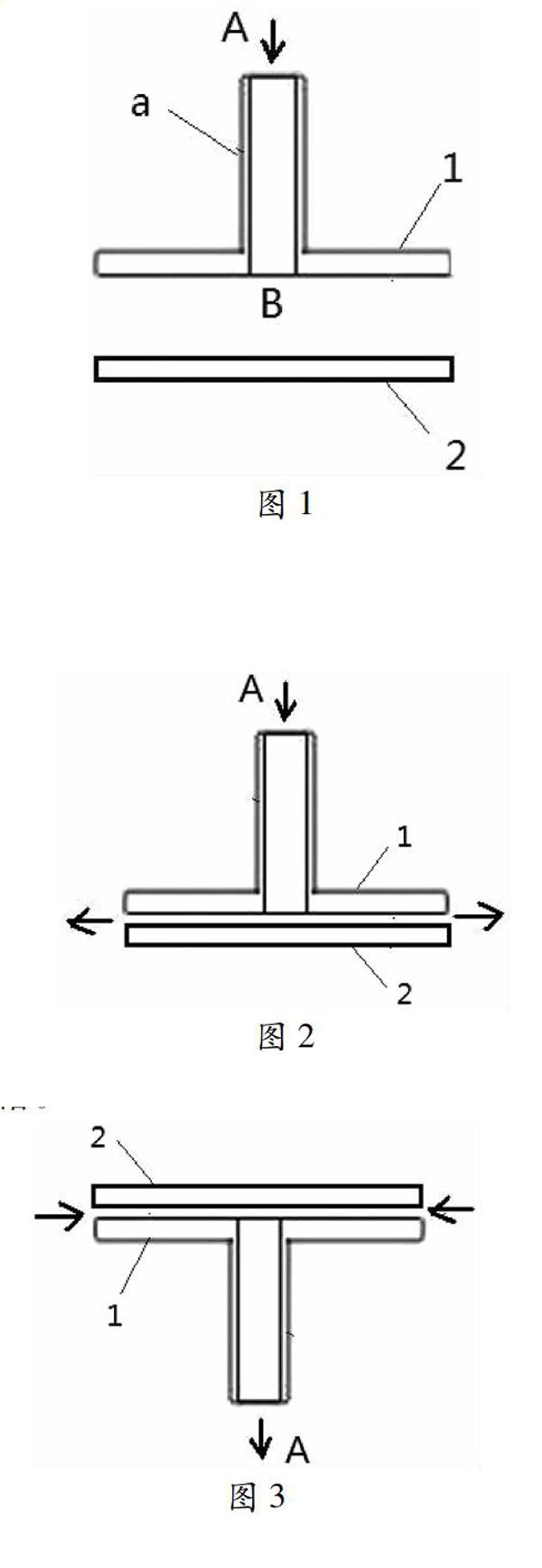
图1所示是实验用设备的剖面图，这个设备由管道a、圆盘1与圆盘2组成。

实验：

如图2所示，使圆盘1保持水平，当圆盘2足够靠近圆盘1时，虽然圆盘1与圆盘2之间仍有间隙，压缩空气也不断从圆盘之间的间隙沿径向向四面八方喷出，但圆盘2却会被圆盘1“吸住”，即便没有支撑，圆盘2也不会掉落。

为什么圆盘1会“吸住”圆盘2？

设圆盘1与圆盘2之间的间隙为H，设间隙中某一点为d，d到圆盘1的轴线的距离为R，设以圆盘1轴线为中心、以轴线到d点的距离R为半径的间隙的体积为V，则

V= HπR2（1）

当圆盘1与圆盘2距离比较近时，从管道喷出的压缩空气充满圆盘与圆盘的间隙，由（1）式可以看出，体积与半径是二次方的关系，当半径增加时，体积将更快的增加。所以，当空气沿圆盘的径向向外运动时，圓盘间隙的体积会更快的增加，这导致空气的体积发生了膨胀。根据理想气体的状态方程可知，在其他的因素不变的情形下，体积增加，则空气的压力降低。而一旦空气压力降低到一定的程度，圆盘2就会被圆盘1“吸住”，而不会下落。

如图3所示，假设空气从四面八方沿径向流入圆盘1与圆盘2的间隙，并从管道的A口流出，根据公式（1）可知，随着空气的径向运动，空气的体积将会更快的缩小，所以空气被压缩，根据理想气体的状态方程可知，圆盘间隙中的空气压力将升高。而一旦其压力高到一定的程度，圆盘2便“漂浮”在圆盘1上，而不会下落。

如图4所示，当圆盘2距离圆盘1比较远时，从B喷出的空气撞击到圆盘2上，沿径向运动离开圆盘2，虽然根据公式（1），空气的体积也在膨胀，但由于圆盘1与圆盘2距离比较大，即便有压力降低，圆盘周围的空气会迅速流入圆盘1与圆盘2之间的空间（如图4双箭头所示），从而破坏压力的降低。不但如此，而且由于从B喷出的空气对圆盘2的冲击，圆盘1与圆盘2之间会表现出互相“排斥”的性质。

如图5所示，向漏斗的入口吹压缩空气，乒乓球就会悬在漏斗口而不会下落。这是因为A处的截面是窄的，而B出截面是宽的，空气由A向B运动的过程中发生了膨胀，因此产生了低压，因而乒乓球被漏斗外的高压托住而不下落。

最后让我们再来看看机翼，如图6所示，机翼是有迎角的，所以机翼下部的流道由宽变窄，因此机翼下部的空气被压缩，压力升高；机翼上部的流道由窄变宽，因此机翼上部的空气被膨脹，压力降低，一高一低，产生机翼升力。这里要注意的是迎角太大也不行，迎角大就如同图4所示的那样，空气就会从机翼尾部流入机翼上部，从而破坏机翼上部的低压，破坏机翼的升力。

此外什么吹一张纸条，纸条向上升起，什么吹两张纸条，纸条彼此靠近等等，这些用的也都是上述空气膨胀与压缩的原理。

参考文献：

[1]郑恩斌.关于机翼升力原因的分析[J]，科技风，2015（5）.