发掘函数级单指令多数据向量化的方法
2017-10-21李颖颖高雨辰翟胜伟李朋远
李颖颖,高 伟,高雨辰,翟胜伟,李朋远
(1.数学工程与先进计算国家重点实验室,郑州 450002; 2.信息工程大学,郑州 450002;3.中国电子科技集团公司 第二十七研究所,郑州 450047; 4.北京跟踪与通信技术研究所,北京 100094)
(*通信作者电子邮箱xdsy213@163.com)
发掘函数级单指令多数据向量化的方法
李颖颖1,2,高 伟1,2,高雨辰1,2*,翟胜伟3,李朋远4
(1.数学工程与先进计算国家重点实验室,郑州 450002; 2.信息工程大学,郑州 450002;3.中国电子科技集团公司 第二十七研究所,郑州 450047; 4.北京跟踪与通信技术研究所,北京 100094)
(*通信作者电子邮箱xdsy213@163.com)
当前面向单指令多数据(SIMD)扩展部件的两类向量化方法分别是循环级向量化方法和超字级并行(SLP)方法。针对当前编译器不能实现函数级向量化的问题,提出一种基于静态单赋值的函数级向量化方法。该方法首先分析程序的变量属性,然后利用一组包括向量函数子句、一致子句、线性子句等编译指示子句指导编译器实现函数级向量化,最后利用变量属性结果对向量化代码进行了优化。从多媒体和图像处理领域选择部分测试用例对所提的函数级向量化的功能和性能在国产申威平台上进行测试,与程序串行执行相比,采用函数级向量化后程序的执行效率更高。实验结果表明函数级向量化可以取得类似任务级并行的加速效果,该方法可以指导自动函数级向量化的实现。
单指令多数据扩展;并行性;函数级向量化;编译指示;静态单赋值
0 引言
单指令多数据(Simple Instruction Multiple Data, SIMD)扩展部件通过一条SIMD扩展指令实现对SIMD向量寄存器中所有数据元素的并行处理,SIMD扩展指令集包括AltiVec、流媒体单指令多数据扩展(Streaming SIMD Extension, SSE)部件、先进的向量扩展(Advanced Vector Extension, AVX)部件、AVX- 512和NEON(ARM架构处理器扩展结构)等[1],国产处理器中龙芯[2]、飞腾[3]、申威以及魂芯[4]也都含有SIMD扩展部件,SIMD扩展部件现已广泛应用于多媒体和科学计算等领域[5]。
虽然手工向量化理论上能够实现最高程度的SIMD向量化[6],但程序员不仅要掌握程序的结构特征和数据布局,还要熟悉目标处理器底层结构和指令集的特点。SIMD自动向量化通过编译器实现程序中可向量执行部分的挖掘,并自动生成面向目标处理器SIMD扩展的向量程序,极大减轻了程序员的工作负担[7]。由于受到编译技术的限制,当前编译器仅从循环和基本块两个粒度挖掘程序中的向量并行性,编译器还不能从函数这个粒度识别程序中的数据级并行[8]。当前的SIMD自动向量化方法主要从循环和基本块两个粒度发掘程序的向量并行性,循环级向量化方法与面向向量机的传统向量化方法相似[9],对其的改进包括外层循环向量化[10]和多面体指导的多重循环向量化[11-12]。超字级并行(Super-word Level Parallel, SLP)是第一个发掘基本块内向量并行性的方法[13]。
目前编译器更多地是发掘循环中蕴含的数据级并行,但为保证正确性,一些情况下编译器并不能把所有的循环都转为向量执行,如:当循环内含有间接数组访问和指针时编译器不能将依赖关系分析清楚;此外当循环内含有函数调用时编译器也可能向量化失败[14]。
函数调用是循环向量化时的一个重大障碍。如下所示的数学库自有函数代码段的循环内含有一个函数调用sin,编译器提供短向量数学库可以对数学函数进行向量化,编译器在作自动向量化时直接调用短向量数学库中的向量版本sin,因此编译器可以对带有sin函数调用的循环成功地进行自动向量化。
#include
#include
#define N 128
double a[N]={0};
double b[N]={1,2,3};
double c;
int main(){
int i;
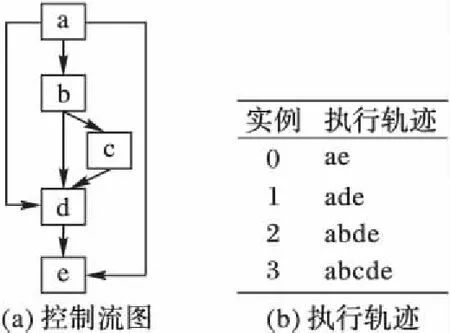
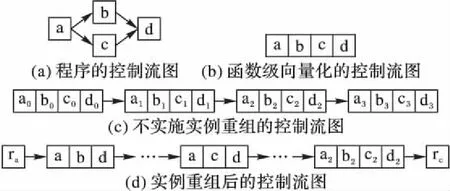
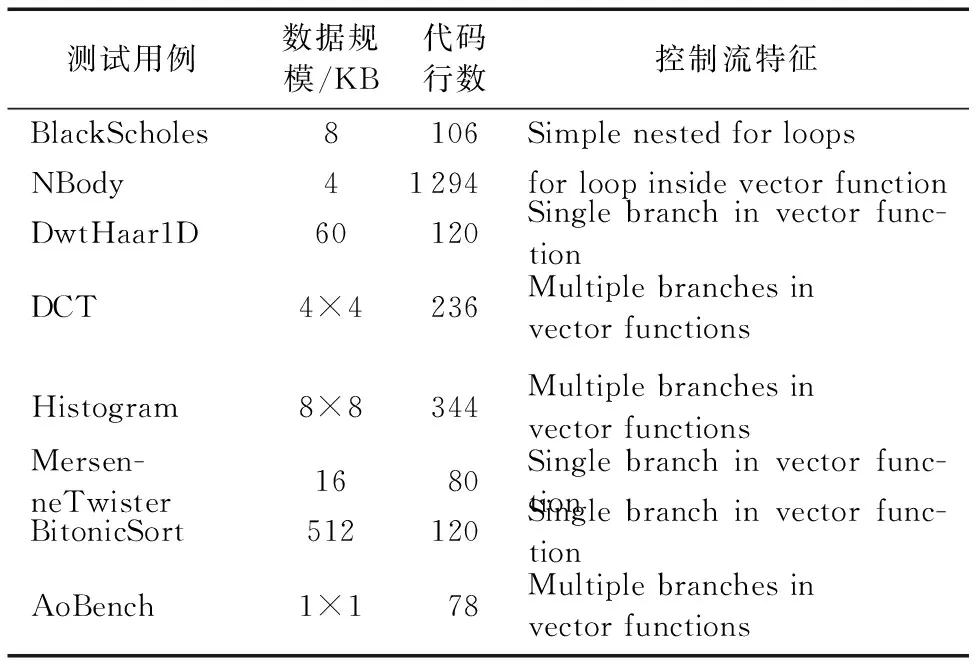
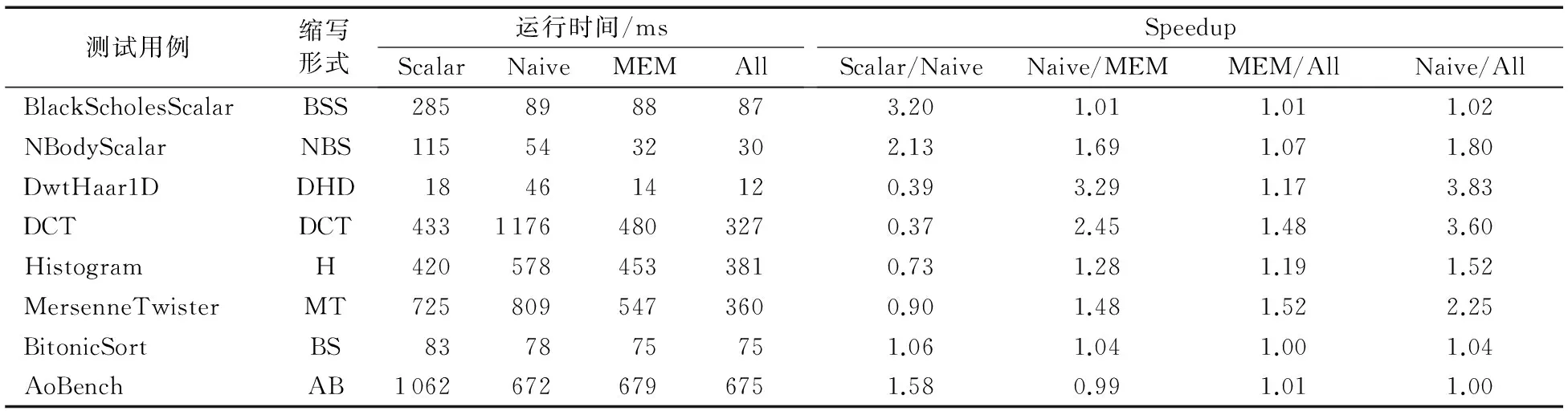
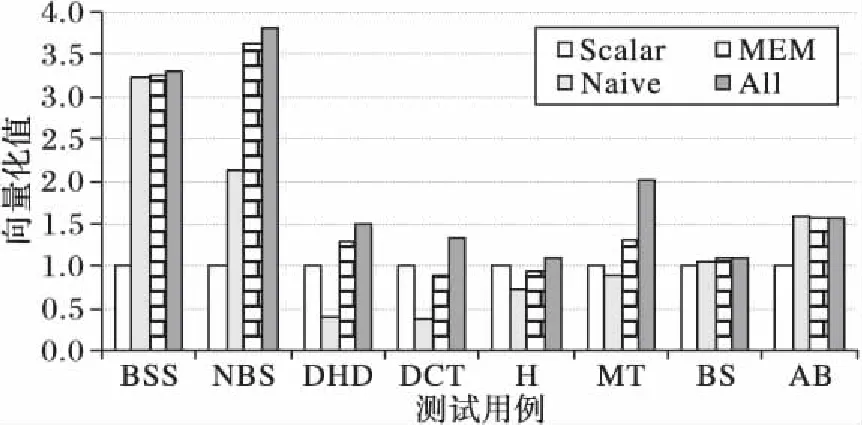
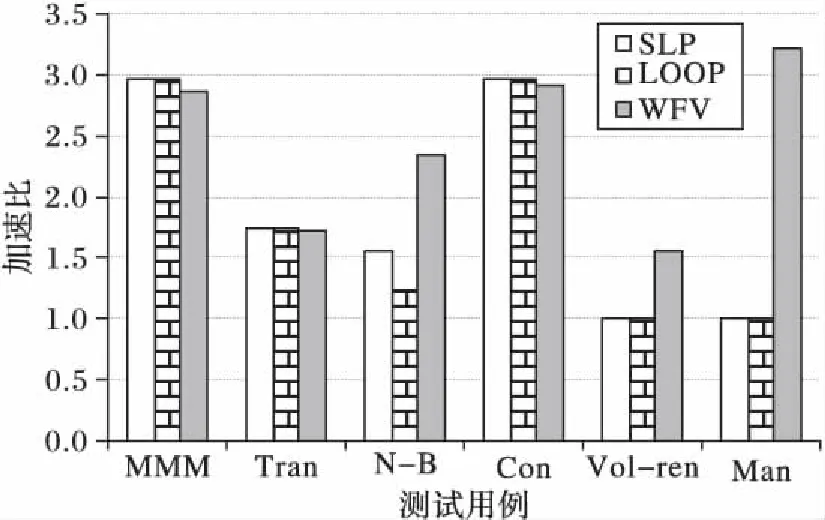
for(i=0;i a[i]=sin(c); } [swvec@cn09 test]MYM tswocc -O3 sin.c -simd=1 (sin.c:10)LOOP WAS VECTORIZED 然而当循环内含有一个用户定义的函数调用时编译器则不能成功地自动向量化。如下所示自定义函数代码段的循环内含有一个用户自定义的函数调用foo_sin,自动向量化时编译器不容易分析清楚函数调用foo_sin会引用和修改哪些变量,除非在调用点上设置内联,否则编译器会保守地不实施自动向量化。 #include #include #define N 128 double a[N]={0}; double b[N]={1,2,3}; double c; double foo_sin(double p){ return sin(p); } int main(){ int i; for(i=0;i a[i]=foo_sin(c); } [swvec@cn09 test]MYM tswocc -O3 sin.c -simd=1 (sin.c:14)LOOP WAS NOT VECTORIZED,LOOP HAS CALLS 为了实现函数foo_sin的向量化,程序员可通过添加编译指示指导编译器完成函数级向量化,编译器会根据标量函数foo_sin生成一个向量函数vfoo_sin,向量化后的循环内调用向量函数vfoo_sin代替原来的标量函数foo_sin,转换过程的示意图如图1所示,假设SIMD扩展部件一次可以处理4个double数据,那么在向量化后的函数调用点处,每4个标量函数调用(foo_sin(x0), foo_sin(x1), foo_sin(x2), foo_sin(x3))由一个向量函数调用vfoo_sin( 图1 标量函数转为向量函数并在SIMD扩展部件上执行Fig. 1 Transfering scalar function into vector function and executing on SIMD extensions 本文提出了一种面向SIMD扩展部件的函数级向量化方法,与现有的面向循环和基本块的SIMD向量化方法相比,本文的主要工作如下: 1)分析了函数级向量化的优点、合法性问题和变量属性; 2)基于静态单赋值形式实现了函数级向量化,并对生成的向量代码进行了优化; 3)给出了一组SIMD扩展编译指示,辅助编译器发掘程序的函数级向量并行性。 1.1 函数级向量化的概念 函数级向量化是将几个相邻的计算实例合并为一个向量操作,实际上是一种单程序多数据模型(Single Program Multiple Data, SPMD),关于SPMD程序当前的研究大都基于统一计算设备架构(Compute Unified Device Architecture, CUDA) 或者开放运算语言(Open Computing Language, OpenCL)等编程模型,并且在图形处理器(Graphics Processing Unit, GPU)上有硬件支持分歧等问题的处理。本文提出的函数级向量化是研究在SIMD扩展部件上运行SPMD程序,由于SIMD扩展部件上没有硬件支持分歧的处理,因而加大了编译的难度。 1.2 函数级向量化的优点 虽然内联替换可以消除函数调用,但是过度的内联替换不仅导致代码膨胀同时也增加了编译时间,因此完全利用内联替换解决含有函数调用循环的向量化问题是不可行的,研究函数级向量化是必要的。当前的SIMD向量化方法是面向循环和基本块发掘程序内蕴含的数据级并行,函数级向量化是从一个更大的粒度识别程序中的数据级并行,并可取得任务级并行的执行效果。循环级向量化方法有很多限制条件,如循环的迭代次数、非正规化的循环、依赖关系等,而这些可能不是函数级向量化的限制条件,函数级向量化相当于从另一个角度重新考虑程序向量执行。此外,函数级向量化还能处理任意复杂的控制流,因此循环级向量化方法不能成功向量化的代码段,或许可利用函数级向量化实现向量执行。 1.3 函数级向量化的难题 候选函数的确定、合法性分析和分歧管理是函数级向量化时的三个难题。 1.3.1 候选函数的确定 判断函数被调用次数是否足够多,如果连续被调用的次数不足够多则不能将其转为向量执行,连续多次函数调用一般仅出现在循环体内。当程序中存在多个函数时,需要根据函数调用图确定函数级向量化的顺序。如果一个函数已经被发掘循环级或基本块级向量并行性,那么进一步实施函数级向量化是困难的。 1.3.2 合法性分析 在对程序中的函数向量化时,保证向量化结果的正确性是困难的,因为需要考虑多个实例对应的函数体之间是否存在阻碍向量执行的依赖,这与编译器中实现循环级向量化时考虑循环内的语句间是否含有依赖环类似,但是判断循环内语句间是否存在依赖环在依赖关系分析中已经有很好的理论基础,并且在编译器中也有实现,而判断多次函数调用之间是否有阻碍向量化的依赖是困难的,因为这涉及到编译中过程间分析和别名分析两大难题。 1.3.3 分歧管理 每一个实例不都是执行完全相同的指令,如图2所示,控制流图(Control Flow Graph, CFG)在4个输入并行执行的情况下,产生执行轨迹。如实例1的执行轨迹为ade,而实例3执行的执行轨迹为abcde,这样产生分歧的控制流使向量执行更为复杂。GPU的分歧管理是有硬件支持的,每一个实例都映射到多核处理器的一个标量核心,由一个中央控制单元控制不活跃实例的结果消除,而在SIMD扩展部件上要求显式的向量执行,编译时需要通过if转换将控制流转为数据流,然后借助SIMD扩展部件中提供的超字选择指令实现谓词执行,进而消除不活跃实例的结果。 图2 不同实例执行的轨迹Fig. 2 Execution path of different instances 1.4 向量属性分析 程序中的变量属性分析包括一致(uniform)、连续(consecutive)、对齐(aligned)、保守(guarded)和不可向量化(nonvectorizable)等。基本块的属性包括全活跃(by_all)、混合(blend)、重连(rewire)、分歧(div_causing)属性。 一个变量是一致的,当且仅当所有的实例中持有相同的值。变量的一致性可以对访存和控制流进行优化。当控制流的判断条件是一致标量时,编译器可以意识到所有的执行代码指令都会经过同一个路径,这样就可以减少分歧控制流带来的掩码执行开销,只需生成超字条件跳转指令即可;如果为一个直接寻址变量则直接利用广播指令生成向量,而不需要利用插入指令逐个值插入到目标向量寄存器中以形成向量。 一个变量是连续的,当且仅当对于所有实例相邻标识符的偏移量是连续的,当基址是一致的,偏移地址是线性连续单元时,编译器可以生成更高效的连续向量访存指令而不需要生成不连续的向量访存如gather/scatter等指令。 一个变量是对齐的,当且仅当所有实例中的第一个实例的地址是SIMD扩展部件宽度 S的倍数。对齐的内存位置SIMD硬件通常提供更高效的向量内存操作,而不对齐的位置则可能需要两次对齐访存和一个拼凑操作,或者直接利用代价更大的不对齐访存指令。 一个基本块具有全活跃属性,当且仅当该基本块被所有的实例执行。如果基本块具有by_all属性,那么它不需要保守执行,因此将生成更高效的代码。混合基本块是指所有实例在这个基本块内汇聚,分歧基本块是指所有实例在这个基本块内产生分歧。重连基本块是指分歧基本块的直接后继或者与之不相交路径的结束块。分歧循环(divergent loop)是指实例在不同的迭代或一次迭代内的不同位置退出循环。 静态单赋值形式(Static Single Assignment, SSA)是一种中间表示,它的单赋值特性表现在每个变量在这种中间表示中仅被赋值一次,SSA使得每个变量都有唯一的定义,因此数据流分析和优化算法可以更加简单。若一个变量有M个定义和N个使用,若不采用SSA,则存在M×N个定义-使用关系,采用SSA则变为M+N。对同一个变量的不相关的若干次使用,在SSA形式中会转变成对不同变量的使用,因此能消除很多不必要的依赖关系,如可消除多数输出依赖和反依赖。由于SSA的中间表示有以上优点,因此本文基于SSA实现函数级向量化。 2.1 函数级向量化转换 函数级向量化转换算法包含四个步骤,分别是掩码生成、选择生成、控制流图线性化和向量指令生成,算法的伪代码如以下所示。 1)掩码生成: Function CreateMasks(Block B) begin if B already has masks then return; end if B is loop header then createMasks(preheader); else foreach P∈predecessors do createMasks(P); end end createEntryMask(B); createExitMask(B); if B is loop header then createMasks(latch) if loop is divergent then Mask latchMask ←ExitMasks[latch→header] EntryMasks[B].blocks.push(latch); EntryMasks[B].values.push(latchMask); end end end 2)选择生成: Function GenerateSelectFromPhi(Phi P,Block B) Begin S←P.values[0]; foreach i=1→P.values.size()-1 do Value V←P.values[i]; Block P←P.blocks[i]; Mask M←ExitMasks[P→B]; S←Select(M,V,S) in B; end replace all uses of P with S; delete P; end 3)控制流图线性化: Function Linearize(Function F) Begin foreach B∈ F do foreach S∈ successors do if NewTargets[B→S].empty() then remove edge B→S; continue; end X←new Blocks; rewire edge B→S to B→X; foreach T ∈NewTargets[B→S]do P←NewTargetDivCausingBlocks[B→S][T]; create edge X→T under condition P; end end end end 4)向量指令生成: Function GenerateCode(Function F) begin foreach op∈function do if op is uniform then generate broadcast; else if op is consectuive then generate unit-stride memory access; else if op is nonvectorizable then generate sequential code; else if op is guarded then generate guarded code; else replace one by one end end end 2.1.1 掩码生成 不同的实例执行时会在一些条件分支发生分歧,而SIMD扩展部件要求所有代码都要执行,所以需要用掩码显式地指出哪些实例执行而哪些实例丢弃执行结果。在控制流图中掩码体现在基本块之间的边上。如果实例i的掩码在控制流图的边A→B为真,那么表示实例i将会执行该分支,因此掩码标志着向量化后向量中的相应元素是有效的数据,这种掩码称为边掩码,用A→B表示基本块A到基本块B的边掩码。边掩码隐含地定义了基本块的入口掩码。若是一个循环头的基本块,那么它的入口掩码是一个来自进入循环的基本块和循环尾部跳转回来的基本块的phi函数。 2.1.2 选择生成 通过在控制流图的汇聚点插入选择操作,以丢弃不活跃实例产生的结果。将原控制流图中的phi函数用选择指令替换,具有n个值的phi函数可以替换成n-1个选择指令。每一个循环要求一个结果向量保留离开循环的实例的循环活跃值,循环活跃值是跨越循环边界的值,即在后续迭代中或循环外使用,可以认为是循环尾基本块的活跃输出变量。对每一个循环活跃值,结果向量通过一个phi函数和一个选择操作两条指令维持,这对于每个循环活跃值仅需插入一个选择指令,而不需要考虑循环出口的个数。结果phi函数被放置在每个嵌套循环的前面,并且有两个输入值,来自循环头的输入值被顶级循环定义。对于嵌套循环,输入值是父循环的结果phi函数,来自循环尾部的输入值是结果更新操作。采用结果向量可以向量化所有循环,包括含有多层嵌套的控制流和多出口的循环。 2.1.3 控制流图线性化 在所有的掩码和选择操作生成之后,控制流已经全部转换为数据流,因此可以将控制依赖边删除。最终在保留原控制流图执行顺序的前提下将所有的基本块线性执行。在原来的控制流图中,如果基本块A在基本块B之前执行,那么在线性化后的控制流图中,基本块A也要放在基本块B之前。如果控制流图分裂为两个分支,那么一条分支的所有基本块必须完整地放在另一分支前面。控制流图线性化的过程有很多策略,不同策略产生代码的效率也不相同,实际中启发式的方法可以考虑代码规模或者寄存器的压力。通过拓扑排序递归地决定基本块的顺序,最后控制流图仅有一个入口和一个出口。 2.1.4 向量指令生成 控制流图线性化后进入到向量指令生成阶段,向量指令生成基本上是一对一的转换,即将标量指令转为向量指令,但是在向量指令生成过程中也需要考虑变量和操作的属性。当变量具有一致属性时,利用广播指令将其转为向量;当变量具有连续属性时,可生成连续的向量访存指令;当变量具有对齐属性时,可生成对齐的向量访存指令;对于不可向量化的操作如存储指令和函数调用等需要复制多次。如果一个块具有全活跃点属性,它会被所有实例执行,因此不需要保守执行。 对于具有保守属性的存操作,需要防止掩码为假时将结果写入内存。为防止实例为假时写入内存,第一种代码生成方法是构建if语句标量执行,但是这种实现方法引入了许多提取、插入和分支操作,降低了向量化收益。第二种代码生成方法是利用“取-拼凑-存”组合操作,取出内存中的数据拼凑后直接存入内存中,对于连续存时此种方法比第一种向量化方法更高效。当不连续存时,如硬件支持生成聚集、分散操作会更高效,最后一种实现方法就是利用硬件支持的掩码内存访问。 2.2 函数级向量化优化 2.2.1 插入超字跳转指令 在进入控制流图线性化阶段时,所有基本块的入口掩码和选择操作select已经设置。此时,基本块入口掩码的值决定着整个基本块指令是否执行。如果入口掩码中所有实例的掩码值均为假,那么可以跳过该基本块的执行而直接执行下个基本块。超字条件跳转指令(Branches-On-Superword-Condition-Codes, BOSCCs) 分为两类:一类是BOA(Branch-On-All),指所有分支都为真时跳转;一类是BON(Branch-On-None),指所有分支都为假时跳转。BOA指令发掘和BON指令发掘过程相似。BOA指令生成算法关键在于识别出一个超字条件所控制的指令区域,而经过掩码生成和控制流图线性化后,基本块的入口掩码已经确定并且基本块已经按照线性顺序组织在一起,因此,采用了线性扫描的方法将识别谓词区域与增加条件跳转操作一起进行。 2.2.2 转为标量执行 如果函数中频繁地有一个或者多个活跃的实例执行而其他实例的结果都被丢掉,那么可以利用实例多版本将其转为串行执行收益可能更大。首先计算出活跃实例的索引,然后将该实例所有需要的值都提到标量寄存器中,最后将结果再更新到结果向量中。虽然标量执行时引入了插入和提取指令,但当向量代码的开销很大时实例多版本是有收益的。此外还可以对标量代码使用SLP方法进行向量化,将同构操作继续转为向量操作。函数级向量化属于水平向量化方法,而SLP方法属于垂直向量化方法,首先需要将活跃实例中的值从原来的向量中提取出来,然后再继续利用打包算法,但这个变换可能涉及到由于数据重组带来的开销。 下面的程序中显示,对两个活跃的实例,首先利用多版本技术将其转为标量执行后再利用SLP方法发掘结果。原代码中的两个操作是相互独立的,如while循环内的else分支所示。函数级向量化后如果仅有两个实例是活跃的,首先计算得到索引的idx0和idx1,将两个实例重新打包成向量,经过加法、减法和乘法等运算后将结果从向量中提取出来,更新到索引idx0和idx1中。 2.2.3 实例重组 假设函数被调用W次,向量化因子为V,函数被向量化后执行的次数为S,那么W、V和S之间的关系为W=V*S。与循环展开类似,S次向量函数调用可以放到一起,相当于向量函数体被执行S次,实例重组就可以在此情况下应用。实例重组就是将所有实例按照真值重新分为真假两组,这样在S次调用中仅有一次需要考虑分歧,而其余S-1次调用在重组后已经确认。实例重组的目标是改进代码的一致性,包括控制流和访存模式。假设程序的控制流图如图3(a)所示,函数级向量化的控制流图如图3(b)所示。如果W=16,V=4,那么S=4,在不实施实例重组的情况下控制流图如图3(c)所示。图3(d)表示实例重组后的控制流图,其中仅有1次调用需要考虑执行块b还是块c这个分歧,而其余3次调用时已经确定或者执行块b或者执行块c,其中块ra和re表示重组代码。 图3 实例重组示意图Fig. 3 Instance restructuring schematic diagram 编译器自动地发掘程序内蕴含的函数级向量并行性是困难的,为了保证函数级向量化的正确性,本文提供一套编译指示帮助编译器实现函数级向量化。这套编译指示不仅包括实现函数级向量化的子句,也包括对向量代码优化的子句如一致子句、连续子句和对齐子句等。 3.1 向量函数子句 在选择向量化哪个函数时,需要判断其被调用的次数是否足够多,如果被调用的次数不是足够多,那么就是因为并行度不够而不能被向量化,连续多次函数调用一般仅出现在循环体内。程序员在发掘函数级向量并行时,首先在循环外加一条指示#pragma simd vec-function,标记该循环虽然存在函数调用但是可以实现函数级向量化。编译指示__decl-vec-function标记后面紧跟着待向量化的函数,编译指示__decl-vec-function的格式如下: _ _decl-vec-function([(vector-clauses)]) vector-clause: uniform-clause linear-clause alignment-clause mask-clause 其中:uniform-clause表示一致子句;linear-clause表示线性之句;alignment clause表示对齐子句;mask-clause表示掩码子句。下面的代码中实现了函数mandel的向量化,首先利用编译指示子句标记函数mandel是一个可向量化函数,同时在出现函数mandel的循环前面添加向量化编译指示,实现了函数mandel的向量化。 _ _decl-vec-function(uniform(max_iter)) unsigned int mandel(complex c,unsigned max_iter); … for(int y=0; y< imageheight;++y){ #pragma simd vec-function for(int x=0; x< imageheight;++x){ count[y][x]=mandel(in_vals[y][x],max_iter); } } 编译器通过识别函数和循环的向量指示子句实现函数的向量化,将函数由标量形式转为向量形式,同时做好过程克隆。编译器中也实现了变量的属性分析,能够识别出变量的一致性、连续性和对齐性等属性,当指示子句给出的属性和编译器自动识别的属性不一致时,根据指示子句给出的属性生成向量代码。 3.2 一致子句 一致子句表示向量寄存器中所有槽位的值相同,相反默认情况下认为所有实例对应的向量寄存器槽位的变量值不同。利用关键字uniform标记一致子句,一致子句格式如下: uniform-clause: uniform(uniform-param-list) uniform-param-list: parameter-name uniform-param-list, parameter-name parameter-name: identifier 3.3 线性子句 线性子句表示变量对应多个实例在内存中引用是连续的,用关键字linear表示。线性子句格式如下: linear-clause: linear(linear-variable-list) linear-variable-list: linear-variable linear-variable-list, linear-variable linear-variable: id-expression id-expression: linear-step linear-step: constant-expression linear-variable中的id-expression应该指派一个标量;linear-step中的constant-expression应该满足或者是一个整数常数表达式,或者是整数类型的变量。如果一个linear-variable没有对应的linear-step,则linear-step的值为1。如果linear-step为一个变量,并且这个变量在循环执行过程中被修改,这样的行为被认为是未定义的。在向量属性的上下文下,linear-step中的constant-expression也应该是整常数表达式,引用linear-step的参数是一致的。 3.4 对齐子句 对齐子句表示变量在内存中引用是对齐的,默认情况下认为变量是不对齐的,利用关键字alignment标记对齐子句,其格式如下: alignment-clause: alignment(uniform-param-list) alignment-param-list: parameter-name alignment-param-list, parameter-name parameter-name: identifier 对齐优化对于发挥SIMD硬件的性能也非常重要,编译器生成更多的向量对齐访问指令对于提升生成的向量程序执行效率有很大帮助,本文的编译器中提出了向量对齐子句,为程序员提供一系列表达对齐的信息。 3.5 掩码子句 默认情况下,对于每一个向量变体需要两种实现:一种是调用时带有掩码条件,另一种是调用时不带掩码条件。如果程序中所有对该函数的调用都是带条件的,则使用掩码子句指导编译器不生成不带掩码调用的函数体;反之,如果程序中所有对该函数的调用都是不带条件的,则使用无掩码子句,指导编译器不生成带有掩码的函数体。掩码子句格式如下: mask-clause: mask nomask 默认情况下编译器会同时生成带掩码的向量函数体和不带掩码的向量函数体,同时使用掩码子句和无掩码子句是无效的。很多时候函数是在条件分支下被调用,如终止递归函数调用的执行,必须生成一个特别的带掩码版本的向量函数并且保证其正确执行。带掩码的向量函数有一个额外的bool型参数,函数体只有当掩码值为真时才被执行。 将本文提出的函数级向量化方法在开源编译器Open64中实现,编译环境为Linux操作系统,版本为Redhat Enterprise 5。实验时首先用Open64编译器 将源程序转化为向量化程序,然后再用基础编译器编译成二进制代码并在国产CPU 申威-1600上运行,最后用串行程序的运行时间除以向量化程序的运行时间便得到向量化的加速比。实验平台CPU主频为2.0 GHz,内存为2 GB,L1数据cache为32 KB,L2 cache为256 KB,基本页面为8 KB,向量寄存器的宽度为256位,可以同时处理4个浮点型数据或者8个整型数据。编译器中还实现了访存和循环等其他优化,通过在程序中添加函数向量化子句指导编译器完成向量化,同时添加对齐、一致、连续等属性指导编译器生成更高效的向量代码。添加函数向量化子句后编译运行获得向量化时间,关闭函数向量化子句后编译运行得到未向量化时间,最后利用未向量化时间除以向量化时间得到函数向量化的加速比。 实验分析包括两部分,分别是优化测试分析和对比测试分析。优化测试分析主要描述访存和控制流等优化对函数级向量化性能的影响;对比测试分析主要将本文提出的函数级向量化方法与现有的循环级和基本块级向量化方法对比。 4.1 优化测试分析 从不同的应用领域选择8个测试用例用于函数级向量化的优化分析测试。这些测试用例覆盖了一系列现实应用,从排序算法到股票分析算法,从粒子运动模拟到图形图像处理。表1列出了这些测试用例的信息,包括输入数据的规则、代码行数、控制流特征和测试用例功能描述。 为了评估访存和控制流等优化对函数级向量化的影响,比较不同优化方案下获得的代码。在不实施函数级向量化时即串行执行,用Scalar表示;将所有的性能优化分析都关闭,称为直接函数级向量化,用Naive表示,直接函数级向量化时关闭所有的优化包括一致属性和访存操作属性;访存优化表示实施函数级向量化时加入了一致、对齐和连续属性,实施了访存优化,用MEM表示;All表示实施了本文提到的所有优化,包括访存相关的一致、对齐和连续属性分析,也包括本文提到的插入超字跳转指令、转为标量执行和实例重组等。 表2是不同优化方案下8个应用的运行时间,单位为ms。其中Speedup的Scalar/Navie表示Navie相对Scalar的加速比,其他依此类推;整体的观察是随着分析和优化的加入,性能在不断增加。图4显示了不同优化方法对函数级向量化的性能测试结果。 表1 优化测试分析用例Tab. 1 Use-case of optimization test and analysis 表2 不同优化的运行时间对比Tab. 2 Running time comparison of different optimizations 图4 不同优化的测试结果Fig. 4 Test results of different optimizations 1)直接函数级向量化(Scalar)。从表2与图4中可以看出,与串行执行相比,即使直接函数级向量化(Naive)也能获得不错的性能加速,如BlackScholesScalar 的向量化加速比为3.20,NBodyScalar的向量化加速比为2.13。这些测试用例是数据密集型应用,带有简单的控制流,这样的测试用例非常适合函数级向量化。然而,DCT的直接函数级向量化加速比仅为0.37,说明其直接函数级向量化的性能弱于标量执行性能,这样的情况有4个例子出现。这种情况的主要原因是生成的向量代码比较保守,所有的访存操作都必须串行执行,所有含有副作用的操作都需要通过if语句生成,所有的控制流都被线性化,这说明了函数级向量化分析和优化的重要性。 2)加入一致、对齐和连续属性访存优化的函数级向量化(MEM)。保留一致性证明是有效的,与直接实施函数级向量化相比,加入一致和连续属性的优化获得的加速比为1.65。对于程序DwtHaar1D、DCT和 NBody,加入一致、对齐和连续属性后,获得了更好的加速效果,但它们的核心内仍有大量的操作保持标量。DwtHaar1D的一个重要性能提升是sqrt操作的参数转为了一致属性,如果这个函数调用没有被标记为一致属性,在直接实施函数级向量化中,它会被保守地执行,因此需要串行执行并且加入条件。连续属性对程序DCT有很好的效果。 3)实施所有优化,包括访存相关的一致、对齐和连续属性分析,也包括本文提到的插入超字跳转指令、转为标量执行和实例重组等。本文最后的优化方案是将所有的优化手段都用上,这包括在控制流图线性化阶段保留部分控制流图,这些控制流图被证明实例不会分歧,这样可以使得更少的代码被执行,向量寄存器压力更小,掩码开销更少。例如在程序Histogram中,循环内存在一个store操作,保守情况下,它需要被串行执行并且需要考虑分歧控制流的影响;然而,这个循环最后被证明不存在分歧,并且会被所有的实例执行。因此在向量化代码生成时生成一个向量存指令,而不是几条标量存指令。 实例多版本和实例重组方法对程序DCT、Histogram和MersenneTwister获得了较好的加速效果,对这三个程序有效果的主要是因为控制流相关的提升,加速比分别为1.47、1.19和1.52。不过这三种优化对没有分歧控制流的程序没有任何优化作用,如程序BitonicSort。与实施一致和连续优化相比,实施多版本和实例重组后加速比平均为1.18。相比直接实施函数级向量化,采用访存和控制流等优化手段后平均加速比为2.00,说明了访存和控制流优化对函数级向量化性能提升有重要作用。 4.2 对比测试分析 从不同的应用领域选择6个测试用例来测试函数级向量化的效果,选择的测试用例包括矩阵乘、矩阵转置和卷积等多媒体领域的典型程序,以及曼德伯特集、光线追踪等图像仿真程序。表3对选择的测试用例进行了描述,包括数据规模、代码行数、控制流特征和程序描述。 表3 对比测试分析用例Tab. 3 Use-case of comparison test and analysis 对选定的测试用例分别实施函数级向量化、循环级向量化和基本块级向量化,测试分析不同向量化方法对选定测试用例的向量化效果,对比测试分析结果如图5所示。图5中函数级向量化方法的测试结果用WFV标记,循环级向量化方法的测试结果用LOOP标记,基本级向量化方法的测试结果用SLP标记。在实施函数级向量化时,已经添加了一致、连续等访存优化和实例重组等其他优化。 图5 对比测试分析结果Fig. 5 Results of comparison test and analysis 图5的函数级向量化性能测试结果显示加速比从1.56到3.22。其中Mandelbrot的加速比为3.22,Convolve的加速比为2.92,矩阵乘MMM的加速比为2.86,这3个程序的函数级向量化加速比较高是因为它们为简单嵌套循环,并且不含有复杂的控制流。N-Body的加速比为2.34,Transpose的加速比为1.72,Volume rendering的加速比为1.56,这3个程序的函数级向量化结果加速比不高是因为它们含有复杂的控制流,在函数级向量化时为了处理分歧引入了许多选择指令,带来了较大的开销,抵消了部分向量化收益;并且由于目标平台不支持聚集、分散等高效的向量访存操作,因此在代码生成时还引入了大量的提取指令进一步抵消了函数级向量化收益。 函数级向量化方法能够成功向量化Mandelbrot,而循环级向量化方法和基本块级向量化方法都不能成功向量化Mandelbrot。这是因为Mandelbrot的最内层为while循环,循环退出条件不定。函数级向量化从一个更大的粒度,将整个while循环成功地进行了向量化。在对N-Body实施循环级向量化时,由于数据跨幅较大导致向量化收益被数据重组抵消较大部分,因此仅获得了1.24的加速比;在对N-Body实施基本块级向量化方法时,由于同构语句数量为3条同时还存在归约操作,导致基本块向量化方法不能充分利用向量寄存器,并且还存在额外的数据重组开销,最后获得了1.56的加速比;而在对N-Body实施函数级向量化时从一个更大的粒度向量化成功,因此获得了2.34的加速比。对Volume rendering函数级向量化方法成功地实施了向量化,并获得了1.56的加速比,而循环级和基本块级向量化都没有向量化成功。对比测试分析的三种向量化方法都成功地向量化了MMM、Convolve和Transpose,但是实施函数级向量化时由于过程间开销导致函数级向量化效果略弱于基本块级和循环级向量化方法,对于这3个程序基于循环展开的基本块向量化方法和循环级向量化方法生成的向量代码基本一致,因此获得的加速比相近。 本文提出了一种发掘函数级SIMD向量化的方法:首先说明了函数级向量化的概念、优点和发掘函数级向量化时的主要问题;然后对函数级向量化时变量的属性进行了分析,基于静态单赋值形式实现了函数级向量化并对生成的向量代码进行了优化;接着提出了一组编译指示子句指导编译器发掘函数级向量化,编译指示子句包括向量函数子句、一致子句、线性子句等;最后从多媒体和图像处理领域选择了6个测试用例来验证本文提出的函数级向量化方法的正确性和有效性。在国产申威-1600平台上进行了性能测试,与程序串行执行相比,采用函数级向量化后程序执行效率比原来串行执行的效率更高。编译器如何自动地实现函数级向量化的发掘以及对函数级向量化的代码优化是下一步的研究工作。 References) [1] 高伟,赵荣彩,韩林,等.SIMD自动向量化编译优化概述[J].软件学报,2015,26(6):1265-1284. (GAO W, ZHAO R C, HAN L,et al. Research on SIMD auto-vectorization compiling optimization [J]. Journal of Software, 2015,26(6): 1265-1284.) [2] 彭飞,顾乃杰,高翔,等.龙芯3B的SIMD编译优化及分析[J].小型微型计算机系统,2012,33(12):2733-2737. (PENG F, GU N J, GAO X, et al. SIMD compiler optimization and analysis based on Godson-3B processor [J]. Journal of Chinese Computer Systems, 2012, 33(12): 2733-2737.) [3] 陈书明,刘胜,万江华,等.协同多核DSP YHFT-QMBase:体系结构及实现[J].中国科学:信息科学,2015,45(4):560-573. (CHEN S M, LIU S, WAN J H, et al. Coordinate multi-core DSP YHFT-QMBase: architecture and implementation [J]. SCIENCE CHINA (Informationis), 2015, 45(4): 560-573.) [4] 王向前,洪一,王昊,等.魂芯DSP的编译器设计与优化[J].电子学报,2015,43(8):1656-1661. (WANG X Q, HONG Y, WANG H, et al. Compiler design and optimization for BWDSP [J]. Acta Electronica Sinica, 2015, 43(8): 1656-1661.) [5] CHEN L, JIANG P, AGRAWAL G. Exploiting recent SIMD architectural advances for irregular applications [C]// Proceedings of the 2016 IEEE/ACM International Symposium on Code Generation and Optimization. Piscataway, NJ: IEEE, 2016: 47-58. [6] LEIßA R, HAFFNER I, HACK S. Sierra: a SIMD extension for C++ [C]// WPMVP ’14: Proceedings of the 2014 Workshop on Programming Models for SIMD/Vector Processing. New York: ACM, 2014: 17-24. [7] HUO X, REN B, AGRAWAL G. A programming system for Xeon Phis with runtime SIMD parallelization [C]// ICS ’14: Proceedings of the 28th ACM International Conference on Supercomputing. New York: ACM, 2014: 283-292. [8] EVANS G C, ABRAHAM S, KUHN B, et al. Vector seeker: a tool for finding vector potential [C]// WPMVP ’14: Proceedings of the 2014 Workshop on Programming Models for SIMD/Vector Processing. New York: ACM, 2014: 41-48. [9] KENNEDY K, ALLEN J R. Optimizing Compilers for Modern Architectures: A Dependence-based Approach [M]. San Francisco, CA: Morgan Kaufmann, 2002. [10] NUZMAN D, ZAKS A. Outer-loop vectorization: revisited for short SIMD architectures [C]// PACT ’08: Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques. Piscataway, NJ: IEEE, 2008: 2-11. [11] TRIFUNOVIC K, NUZMAN D, COHEN A, et al. Polyhedral-model guided loop-nest auto-vectorization [C]// PACT ’09: Proceedings of the 18th International Conference on Parallel Architectures and Compilation Techniques. Piscataway, NJ: IEEE, 2009:327-337. [12] KONG M, VERAS R, STOCK K, et al. When polyhedral transformations meet SIMD code generation [C]// PLDI ’13: Proceedings of the 34th ACM SIGPLAN Conference on Programming Language Design & Implementation. New York: ACM, 2013: 127-138. [13] LARSEN S, AMARASINGHE S. Exploiting superword level parallelism with multimedia instruction sets [J]. ACM Sigplan Notices, 2000, 35(5): 145-156. [14] WANG Y, WANG D, CHEN S, et al. Iteration interleaving-based SIMD lane partition [J]. ACM Transactions on Architecture & Code Optimization, 2016, 12(4): Article No. 58. LIYingying, born in 1984, M. S., lecturer. Her research interests include advanced compilation technique. GAOWei, born in 1988, Ph. D candidate. His research interests include high performance computing, advanced compilation technique. GAOYuchen, born in 1988, M. S. candidate. His research interests include advanced compilation technique. ZHAIShengwei, born in 1982, M. S., engineer. His research interests include advanced computing. LIPengyuan, born in 1989, M. S., researcher. His research interests include high performance computing. Methodforexploitingfunctionlevelvectorizationonsimpleinstructionmultipledataextensions LI Yingying1,2, GAO Wei1,2, GAO Yuchen1,2*, ZHAI Shengwei3, LI Pengyuan4 (1.StateKeyLaboratoryofMathematicalEngineeringandAdvancedComputing,ZhengzhouHenan450002,China;2.PLAInformationEngineeringUniversity,ZhengzhouHenan450002,China;3.The27thResearchInstitute,ChinaElectronicsTechnologyGroupCorporation,ZhengzhouHenan450047,China;4.BeijingInstituteofTrackingandTelecommunicationsTechnology,Beijing100094,China) Currently, two vectorization methods which exploit Simple Instruction Multiple Data (SIMD) parallelism are loop-based method and Superword Level Parallel (SLP) method. Focusing on the problem that the current compiler cannot realize function level vectorization, a method of function level vectorization based on static single assignment was proposed. Firstly, the variable properties of program were analysed, and then a set of compiling directives including SIMD function annotations, uniform clauses, linear clauses were used to realize function level vectorization. Finally, the vectorized code was optimized by using the variable attribute result. Some test cases from the field of multimedia and image processing were selected to test the function and performance of the proposed function level vectorization on Sunway platform. Compared with the scalar program execution results, the execution of the program after the function level vectorization is more efficient. The experimental results show that the function level vectorization can achieve the same effect of task level parallelism, which is instructive to realize the automatic function level vectorization. Single Instruction Multiple Data (SIMD) extension; parallelism; function level vectorization; compiler directive; static single assignment TP301.6; TP311.53 A 2016- 12- 29; 2017- 03- 21。 李颖颖(1984—),女,河南郑州人,讲师,硕士,主要研究方向:先进编译技术; 高伟(1988—),男,黑龙江齐齐哈尔人,博士研究生,主要研究方向:高性能计算、先进编译技术; 高雨辰(1988—),男,河南郑州人,硕士研究生,主要研究方向:先进编译技术; 翟胜伟(1982—),男,河南郑州人,工程师,硕士,主要研究方向:先进计算; 李朋远(1989—),男,河南焦作人,研究员,硕士,主要研究方向:高性能计算。 1001- 9081(2017)08- 2200- 09 10.11772/j.issn.1001- 9081.2017.08.2200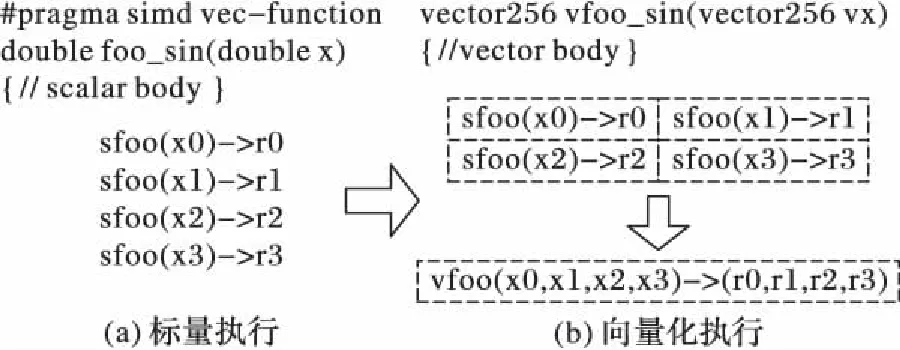
1 函数级向量化分析
2 基于静态单赋值形式的函数级向量化

3 编译器中实现
4 实验结果与分析

5 结语
