基于水声通信的新型变步长最小均方算法

郑奕丰，郝学元，颜晓红

(南京邮电大学 电子科学与工程学院，南京 210000)

(*通信作者电子邮箱1215022635@njupt.edu.cn)

基于水声通信的新型变步长最小均方算法

郑奕丰*，郝学元，颜晓红

(南京邮电大学 电子科学与工程学院，南京 210000)

(*通信作者电子邮箱1215022635@njupt.edu.cn)

在水声通信中，信道的多径效应会造成严重的码间串扰(ISI)，而现有的均衡算法在处理ISI问题时存在收敛速度慢、稳态误差大、算法复杂不易于硬件移植等问题，为此结合判决反馈均衡器结构前向均衡(FFE)与判决均衡结构(DFE)，提出了一种基于反余弦步长函数和三参数调整因子的变步长最小均方(LMS)算法。首先对三参数因子α、β、r进行算法仿真，优化算法性能，与固定步长LMS算法、基于修正反正切的变步长LMS算法以及基于双曲正割函数的变步长LMS算法的收敛性能和稳态误差进行仿真比较，结果显示：所提算法的收敛速度较固定步长LMS算法提高了57.9%，稳态误差下降5 dB；较双曲正割LMS算法和修正反正切LMS算法提高了26.3%和15.8%，并且算法的稳态误差下降了1～2 dB。最后，将算法移植于信号处理模块，进行水下实验，结果表明，水声信道造成的ISI经过均衡器后，信号得以恢复，能够实际克服多径效应造成的水声信道ISI问题。

水声通信；码间串扰；最小均方均衡算法；变步长函数；判决反馈均衡器

0 引言

水下中远距离通信，例如水下勘探、水中人工作业、水下通信网建设等，由于排线困难、维护成本高，一般选用水声无线通信的方式。数据通过水声换能器发射进入复杂的海洋信道经由数百米至数千米传达至水下信宿，复杂多变的水文环境给接收数据带来了严峻的挑战。由于声波的波速在海水中只有约1 500 m/s，比电磁波低了五个数量级，信道过程中信号的衰减、多普勒频移、多径效应等都将直接影响接收端的信噪比(Signal-Noise Ratio，SNR)和误码率(Bit-Error Rate, BER)。而多径效应造成的码间串扰(Inter-Symbol Interference， ISI)问题则成为水声通信中影响最大也最困难的问题[1]。此项研究对水声通信的发展有重要意义。

自适应均衡技术可以有效地消除码间干扰，抵消信道失真，利用自适应均衡技术来修正水声信道传输过程中信号的畸变和失真，是目前水声通信领域中普遍采用的方法。最小均方(Least Mean Square，LMS)算法因其较低的计算复杂度、在平稳环境中的收敛性良好以及易于硬件实现等主要特征，是自适应滤波理论中应用最广泛的算法，并在相干水声通信中被普遍应用[2-3]。文献[4]提出了一种归一化的LMS算法，该算法通过对输入样本和误差进行归一化得到了较快的收敛速度。文献[2]提出了一种基于自适应混合能量参数的变步长LMS水声信道均衡算法，通过引入能量混合参数，调整步长变化。文献[5]提出了改进的记忆快速自优化均衡(Memory Fast-Optimized LMS, MFOLMS)算法，根据前向的判决结果调整步长参数，提高了均衡器跟踪信道变化的能力和收敛速度。

本文针对水声通信中的码间串扰问题，从变步长函数的优化入手，结合判决反馈均衡器结构前向均衡(Feed-Forward Equalizer， FFE)与判决均衡结构(Decision Feed-Back Equalizer, DFE)，提出了一种基于反余弦函数的三参数变步长LMS算法，提高了算法的收敛性能，并保证了算法的稳态误差在10-4个码元数量级。

1 水声通信

水声通信即在水下环境中，以声波作为载波，进行调制后于水声信道中传播，在接收端通过水声换能器进行接收，经过滤波器组解调还原基带信号，达到通信目的。下面分别介绍水声信道模型和信道均衡原理。

1.1 水声信道模型

水声信道有多种模型，如声线模型、简正波模型、快速场模型、抛物方程模型等[6]。

近年来的因射线理论计算简洁，能适应各种信道条件的特性，被水声通信建模广泛采用；同时基于实际应用中一般符合高频、浅水、点声源的特点，本文对水声通信的研究选用射线模型。射线模型不考虑声波的波动性质，认为声线是时刻与波阵面垂直传播的射线[7]。从声源发出的声线按一定的路径到达接收点,接收点接收到的声场是所有到达该点声线的叠加。基于我们选用的水声信道射线理论，水下信道的多径冲激响应函数h(t)为:

(1)

式(1)等号右边第一项表示水声多径中主路径的冲击响应，第二项为其他所有路径函数的求和。其中：Ai表示第i条路径上声波的衰减因子，τi表示第i条路径上信号的时延，δ(t)为迪克拉函数。函数(1)揭示了水声信道中码间串扰造成的原因：不同路径上的声线强度和时延不同，所有路径上的声线在信道的终点叠加，造成前后码元的互相叠加干扰，将会严重影响水下通信的质量[8]。

1.2 信道均衡原理

调制信号经过水声信道传播后经接收端接收到的信号为信源信号及信道噪声与信道冲激响应h(n)的卷积，可以表示为：

r(n)=v(n)*h(n)+u(n)

(2)

其中：r(n)为n时刻信源接收到的码元，v(n)为信源输出的信号，h(n)为信道的冲激响应，u(n)为信道噪声。理想状态下的信道接收到的码元r(n)应和v(n)相同，而实际情况是，经过信道冲激响应、信道噪声的干扰，码元失真了，为了恢复原始信号，必须在接收端引入信道均衡滤波器，其原理如图1所示。

图1 信道均衡原理图Fig. 1 Principle diagram of channel equalization

信道均衡的原理是通过均衡滤波器产生一个与信道特性相反的，能够抵消信道衰弱的冲激响应来中和信道对信号的干扰，使得信道响应和均衡器响应的卷积近似于狄克拉函数δ(n-n0)，从而使得输出信号近似于原始信号。经过均衡器滤波后的信号表达式为：

y(n)=r(n)*W(n)=

r(n)*h(n)*w(n)+u(n)*W(n)≈

r(n)*δ(n-n0)+u(n)*W(n)

(3)

其中：y(n)为均衡器的输出，W(n)为均衡滤波器的权系数。可以看出在通信过程中，其他参数都无法人为控制，只有通过改进均衡滤波器的权系数才可能提高通信质量，因此，在本文以及其他水声信道均衡方面的研究也都是围绕均衡器权系数算法展开的。

2 基于LMS的变步长水声多径均衡算法

2.1 传统LMS算法

传统的LMS算法基于最小均方误差准则和最速下降法，直接以误差平方的期望值作为梯度的估计值，并沿着梯度负方向迭代，直到令迭代函数收敛。

其均衡器权系数迭代公式为：

W(n+1)=W(n)+2ue(n)*x(n)

(4)

其中：u为固定的步长因子，权系数仅根据输入序列x(n)和误差e(n)按比例调整均衡器权系数。其均衡器结构如图2所示。

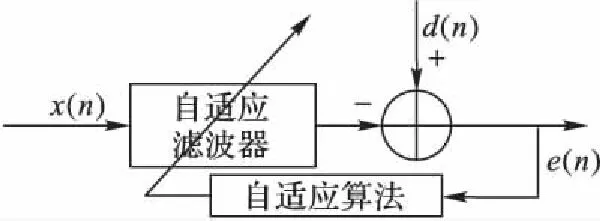
图2 自适应均衡滤波器结构示意图Fig. 2 Structure diagram of adaptive equalization filter

2.2 FFE-DFE结构均衡器

FFE-DFE判决反馈均衡器是一种结合了传统FFE线性均衡器和DFE非线性均衡器的均衡结构[9-10]，由两级滤波器组成，即FFE前馈滤波器和DFE反馈滤波器。相比传统的线性均衡器，DFE利用了前一个码元的判决输出来校正当前的码元，相当于获得了更多的信道先验信息，均衡性能更好；而FFE判决反馈均衡器结构简单，易于计算，简化了传统的DFE均衡器，收敛性能更好。结合两者优势，FFE-DFE均衡结构能够获得更好的性能。FFE-DFE均衡器的表达式为：

(5)

其中：s(i)是对i个信号码元的估计值，FFE前馈滤波器阶数为m，DFE反馈滤波器阶数为n，Ck和bl分别为前馈滤波器和反馈滤波器的抽头系数。FFE-DFE均衡器结构如图3所示。

在不同的信噪比初始条件下，对未经均衡的、经过FFE前馈滤波结构均衡、经过DFE判决反馈滤波器结构均衡和经过FFE-DFE组合判决反馈滤波器均衡四种情况下的通信误码率进行仿真,仿真结果如图4所示。可以看出使用均衡器的三种结构的通信误码率都要小于不使用均衡算法的通信系统，而FFE-DFE结构显然对于降低通信误码率有着更好的性能，对于码间串扰造成的高误码率的水声信道来说， FFE-DFE组合结构是更好的选择。

图3 FFE-DFE判决反馈结构Fig. 3 Feedback structure of FFE-DFE decision

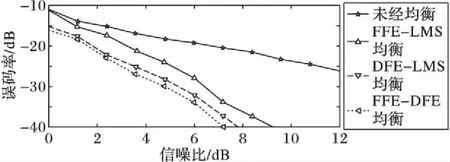
图4 均衡器误码率曲线Fig. 4 Equalizer BER curve

2.3 变步长LMS算法

由式(1)的水声信道冲激响应函数可以看出，水声信道中由于其多径效应，信道环境变得非常复杂，多径上多条声线的强度和时延都是时变和空变的；而且声波在传播过程中，不论是衰减和时延都是不确定的。这就要求算法能够根据误差调整均衡器步长，做到尽快收敛。

近年来对LMS算法的研究的重点主要集中在步长的选取上，通过调整步长的迭代方式，可以得到更好的算法收敛性和稳定性[2,8]。传统的LMS算法步长固定，虽然计算简单，但是收敛性和稳定性难以同时兼顾，大步长的选取会造成稳态误差增大，小步长虽然稳态误差减小，但是收敛变慢。文献[11]提出了一种归一化最小均方(Normalized Least Man Square， NLMS)误差算法，它通过使用可变的步长因子，对算法进行优化，但是在水下强相关信道下，算法收敛性受到严重影响。文献[12]提出了一种改进型的S函数变步长LMS算法(Sigmoid Variable Step-size Least Mean Square， SVSLMS),提高了算法收敛速度，达到了较好的收敛性；但在函数趋向收敛后稳态误差较大，算法的稳定性较差。文献[8]提出了一种基于反正切步长迭代函数的LMS算法：

u(n)=β·arctan(α|x(n)e(n)e(n-1)e(n-2)|)

(6)

该算法使用了FFE-DFE相结合的均衡器模型，与NLMS算法相比性能有了很大的提升；但是算法的计算量较大，当前码元的计算精度依赖于前级码元，不适用于低速且ISI相当严重的水声信道。文献[13]提出了一种基于修正反正切函数的变步长LMS算法，通过在反正切函数上加一个r次幂，使得步长函数更为平坦，函数的收敛性能更好；但是函数形式比较复杂，移植到实际应用中较为困难。

这些变步长算法都是选取了一个合适的步长迭代函数，并加入了调整参数，使得在算法在初始阶段拥有大步长和较快的收敛速度，算法的优化的主要方向也是提高算法的速度、降低算法的稳态误差、降低算法的复杂度以及考虑算法的可移植性。

2.4 改进的新型LMS变步长算法

本文总结前人的经验，结合上述实际问题，对算法进行优化，引入了反余弦函数迭代公式。反余弦函数是一个自变量在零值附近时梯度变化缓慢的函数，而算法对码元的估计误差是在(0,1)区间，在这一区间，函数及函数的导数自增，这一特性使得在误差较大时函数值较大，误差趋于0时函数值接近于0,因此使用反余弦函数作为算法步长迭代公式的函数基底，使算法在误差较大时保证较大的步长，以提高收敛速度；而在误差趋于0时减小步长，减缓收敛速度，保证算法的稳定性。在此基础上，算法引入三个误差调整因子来调整反余弦函数边界, 使得在误差较大、函数值较大时保证函数不发散；调整了步长因子和误差e(n)的非线性函数关系，提出了一种基于反余弦函数的三误差调整参数的快速收敛变步长LMS算法；最后与其他算法进行对比，以验证算法的优势。

算法的表达式如下：

e(n)=d(n)-y(n)=d(n)-xT(n)·w(n)

(7)

u(n)=β·arccos(α|er(n)|)

(8)

w(n+1)=w(n)+2u(n)e(n)x(n)

(9)

式(7)为误差函数，其中：d(n)是第n个码元的期望信号,y(n)为经过均衡器后的判决输出，w(n)是均衡器权系数，x(n)为原始基带信号，误差信号e(n)为期望信号与判决输出的差值。式(8)为三误差调整参数的步长迭代公式，其中arccos为反余弦函数，α、β和r为调节参数,u(n)为步长因子，通过e(n)和三参数反余弦函数对步长因子进行实时的迭代修正，使得对每一时刻的码元的迭代步长都趋于合理。由于反余弦函数形式简单，计算量少，并且误差函数e(n)和步长因子u(n)满足反余弦函数形式，函数在e(n)较大时，取得较大步长，收敛迅速；在e(n)变小时，步长也平稳变小，可以保证稳态误差更小，兼顾了收敛速度和稳态误差。

为了确定合适参数范围，基于FFE-DFE结构使用Matlab对α、β和r三个参数分别进行仿真分析[8]，输入信号为二进制调制信号，滤波器权系数设置为W=[0.8,0.5],阶数为2，噪声为方差为0.5的高斯白噪声，取1 000个采样点，独立仿真100次并取统计平均，通过e(n)和u(n)的关系，以及均衡器收敛曲线，确定算法合适的参数。仿真结果如图5～10所示。

图5、7和9展示了三误差调整参数对步长因子数值的影响，图6、8和10展示了三误差调整参数对算法收敛的影响，并将结果归纳表示于表1。其中由图5可以看出α参数能够调整步长函数的开口大小，由图7可以看出β参数直接线性影响了步长函数的函数值大小，由图9可以看出r参数调整了步长函数的底部平滑程度。通过仿真三参数因子对函数曲线的调整、不同参数值时算法的收敛性能以及函数收敛稳定后的误差，根据表1归纳结果，综合考虑收敛步长和稳态误差，确定本文算法在该仿真条件下的最优参数为α=0.8，β=0.000 4，r=1.4。从图6、8和10可以看出，在取最优参数时，算法在初始阶段的均方误差e(n)较大,对应的步长因子u(n)也较大,算法快速收敛；当迭代进行250次左右时，算法基本收敛，此时步长调整变小，算法进入稳态，误差e(n)达到了最小值，稳态误差保持在-25 dB数量级。

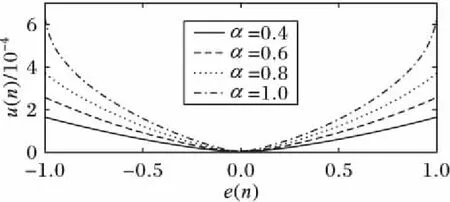
图5 u(n)和e(n)的关系曲线(β=0.000 4，r=1.4)Fig. 5 Relation curve of u(n) and e(n) (β=0.000 4，r=1.4)

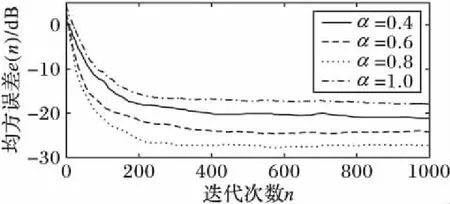
图6 不同α值的收敛曲线(β=0.000 4，r=1.4)Fig. 6 Convergence curve of different α (β=0.000 4，r=1.4)

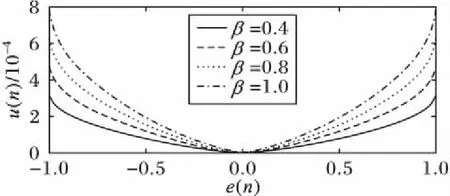
图7 u(n)和e(n)的关系曲线(α=0.8，r=1.4)Fig. 7 Relation curve of u(n) and e(n) (α=0.8，r=1.4)

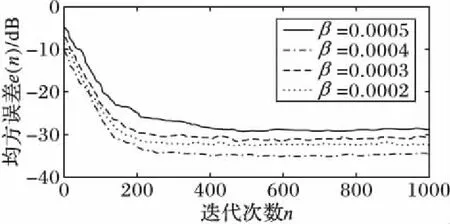
图8 不同β值的收敛曲线(α=0.8，r=1.4)Fig. 8 Convergence curve of different β (α=0.8，r=1.4)

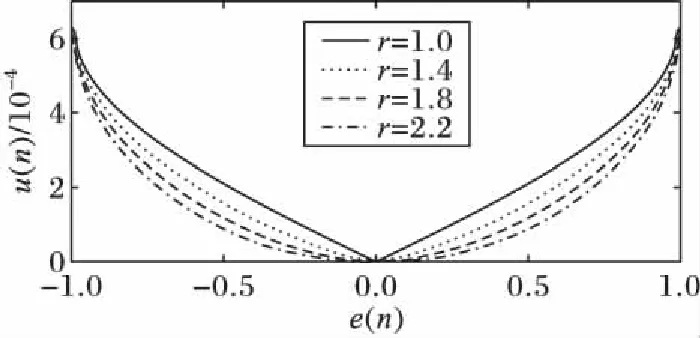
图9 u(n)和e(n)的关系曲线(α=0.8，β=0.000 4)Fig. 9 Relation curve of u(n) and e(n) (α=0.8，β=0.000 4)

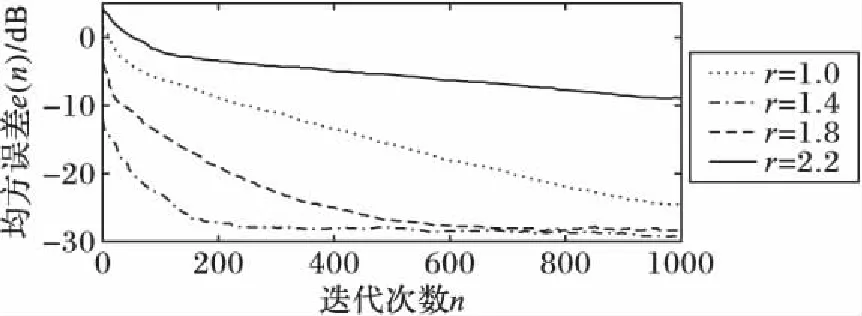
图10 不同r值的收敛曲线(α=0.8，β=0.000 4)Fig. 10 Convergence curve of different r (α=0.8，β=0.000 4)表1 三误差调整参数对比Fig. 1 Comparison of three adjustment parameters

参数α(β=0.0004,r=1.4)收敛步长稳态误差/dB最优值参数β(α=0.8,r=1.4)收敛步长稳态误差/dB最优值参数r(α=0.8,β=0.0004)收敛步长稳态误差/dB最优值0.4405-18—0.0002210-31—1.0不收敛——0.6420-23—0.0003220-30—1.4230-27r=1.40.8270-27α=0.80.0004210-33β=0.00041.8580-26—1.0260-15—0.0005390-27—2.2不收敛——

2.5 算法性能对比与分析

文章[14]中提出了一种基于双曲正割函数的变步长LMS算法，该算法相对传统的LMS算法以及归一化LMS算法(NLMS)等具有更好的收敛性能和稳定性，将此算法称之为算法1；基于修正反正切函数的变步长LMS算法[13]提出了一种基于修正反正切函数的变步长LMS算法，该算法已证明在以反正切函数为基底的多种LMS算法中，具有最好的收敛性能和抗噪声性能，将此算法称为算法2。

对上述两种算法以及传统的固定步长LMS算法进行收敛性能对比，结果如图11所示。从图中可以看出，几种改进的变步长LMS算法与传统的LMS算法相比，收敛速度及稳态误差性能都有显著提升。以算法100次迭代内不出现3 dB(约5倍)以上的均方误差浮动作为算法达到稳定的标志，以算法稳定后的均方误差的平均期望作为算法的稳态误差，以算法首次达到该稳态误差时的迭代次数作为算法的收敛步长。结合FFE-DFE组合结构，使用本文提出的基于反余弦函数的变步长LMS算法，得到收敛步长约为171，较固定步长LMS算法约406步的收敛步长缩短了235步，收敛速度提高了约57.9%，算法的均方误差下降了5 dB；较算法1收敛步长缩短了61步，较算法2缩短了约32步，收敛速度分别提高了26.3%与15.8%，稳态误差较两种变步长算法下降了1～2 dB。

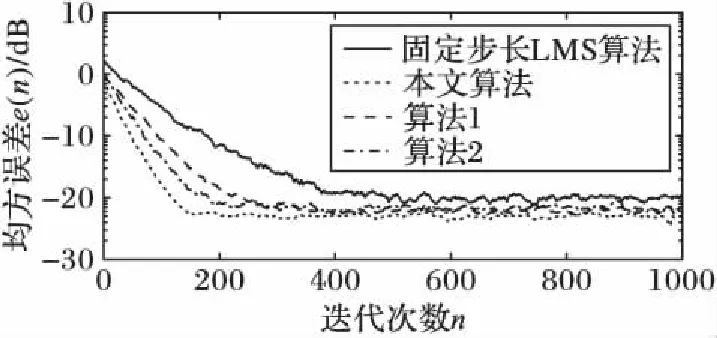
图11 四种算法性能对比Fig. 12 Performance comparison of four algorithms

3 实物验证

为了对变步长自适应均衡算法性能进行检验，我们使用ARM(Acorn RISC Machine)信号处理模块移植了Matlab环境下仿真的反余弦变步长LMS算法，并结合了FFE-DFE非线性均衡器结构在实际的水文条件下进行了水声实验，算法流程如下所示，算法开始时，需要约200个训练序列使算法收敛进入稳态，然后进入自适应均衡，矫正信道误码。 其中:输入参数为训练序列X,长度记为Lx，单帧计算码元数量为L；前馈均衡器阶数为nW，反馈均衡器阶数为nB；前馈滤波器初始学习步长为stepw,反馈滤波器初始学习步长为stepb；e为计算误差；d为期望输出；y为组合判决输出(训练序列传输完之前，d直接从训练序列得到)；X′为训练序列结束后实际的信道传输信号；Lx′为信道传输信号序列长度。

实验于安静的清晨在河流中进行，基本排除了周围的噪声干扰，河道水流流速较快，水面有可见的漩涡，且测试点附近具备桥洞、石块等障碍物，具备声波反射条件，属于强多径干扰下的水声信道。发射装置置于水下3 m，接收装置置于水下2 m，水平间距350 m，收发装置固定在岸边，并随水流有随机摆动。

发送端使用简单的脉冲宽度调制(Pulse Width Modulation，PMW)方式调制基带信号，并发出40 kHz的声波。接收端FFE前馈均衡器阶数为32，DFE反馈均衡器阶数为20，接收到经过信道衰减的波形后，进行均衡处理。信源发出的基带信号如图12(a)所示(码元序列为10100 01010 10001 01010 00101)，经信道传输后的波形如图12(b)所示，其中实线为接收机接收到的信号，虚线为直接进行抽样判决后的数字信号(码元序列为01110 11101 10010 10110 01101)，对比图12(a)与图12(b)可以看出信号在经过水声信道后出现了严重的码间串扰，25个码元中的误码数量达到了13个，误码率(BER)达到了52%。经过均衡后的判决输出如图12(c)所示，对比图12(a)和图12(c)，可以看出信号恢复很好。

4 结语

针对目前应用于水声通信的信道均衡算法收敛速度慢、存在稳态误差的性能瓶颈以及算法复杂不易于硬件移植等问题，提出了计算简洁、具有更快收敛速度和稳定性的反余弦变步长LMS算法，并通过仿真和实物实验验证了算法性能。但是本文算法对水声信道中的噪声干扰考虑不足，仅以高斯白噪声作为噪声输入，在后续工作中，会考虑实际情况下的噪声问题，研究在低信噪比下的水声信道快速收敛均衡算法。

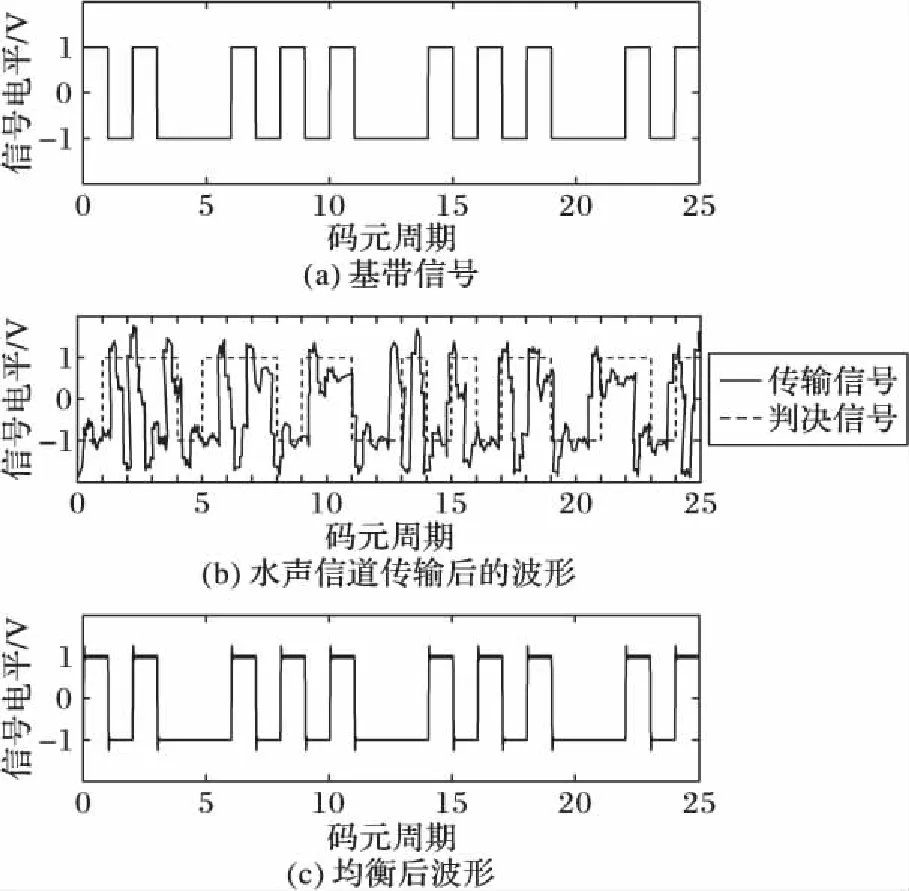
图12 实验波形Fig. 12 Experimental waveforms

References)

[1] 程恩,袁飞,苏为,等.水声通信技术研究进展[J].厦门大学学报(自然科学版),2011,50(2):271-275. (CHENG E, YUAN F, SU W, et al. Research on technology of underwater acoustic communication [J]. Journal of Xiamen University (Natural Science), 2011, 50(2): 271-275)

[2] 宁小玲,张林森,刘志坤,等.基于自适应混合能量参数的变步长LMS水声信道均衡算法[J].系统工程与电子技术,2015,37(9):2141-2147. (NING X L, ZHANG L S, LIU Z K, et al. Variable step size LMS equalization algorithm based on adaptivemixed-power parameter in underwater acoustic channels [J]. Systems Engineering and Electronics, 2015, 37(9): 2141-2147.)

[3] 杜欣,张效民,赵延安,等.一种变步长LMS算法在远程水声通信中的研究应用[J].计算机测量与控制,2009,17(6):1178-1180. (DU X, ZHANG X M, ZHAO Y A, et al. Experimental research on long range underwater acoustic communication with variable step size LMS algorithm [J]. Computer Measurement & Control, 2009, 17(6): 1178-1180.)

[4] 宁小玲,刘忠,罗亚松,等.水声信道快速收敛自适应均衡算法[J].系统工程与电子技术,2010,32(12):2524-2527. (NING X L, LIU Z, LUO Y S, et al. Fast convergent adaptive underwater acoustic channel equalization algorithm [J]. Systems Engineering and Electronics, 2010, 32(12): 2524-2527.)

[5] 李记龙,冯海泓,黄敏燕.强多径干扰下的水声通信均衡算法研究[J].声学技术,2016,35(1):73-77. (LI J L, FENG H H, HUANG M Y. Research of underwater acoustic communication equalization algorithm under the strong multipath interference [J]. Technical Acoustics, 2016, 35(1):73-77.)

[6] 胡作进,王昌明,杨善林,等.水声信道的多模型模拟和试验[J].计算机仿真,2004,21(5):92-94. (HU Z J, WANG C M, YANG S L, et al. Underwater acoustic channel model simulation and experiment [J]. Computer Simulation, 2004, 21(5): 92-94.)

[7] 王峰,赵俊渭,鄢社锋.基于射线模型的水声信道的仿真软件设计[J].电声技术,2002(6):8-10. (WANG F,ZHAO J W,YAN S F. Software design of underwater acoustic channel simulation based on ray model [J]. Audio Engineering, 2002(6): 8-10.)[8] 孙博,程恩,欧晓丽.浅海水声信道研究与仿真[J].无线通信技术,2006,15(3):11-15. (SUN B, CHENG E, OU X L. Research and simulation of neritic underwater acoustic channel simulation [J]. Wireless Communication Technology, 2006, 15(3):11-15.)

[9] 郝学元,颜晓红,钱丽霞.一种自适应前向均衡与判决均衡组合结构及变步长改进算法[J].物理学报,2015,64(23):238402. (HAO X Y, YAN X H, QIAN L X. The novel feed forward and decision feedback equalizer structures and improved variable step algorithm [J]. Acta Physica Sinica, 2015, 64(23): 238402.)

[10] ALFIAD M S, VAN DEN BORNE D, KUSCHNEROV M, et al. FFE, DFE and MLSE equalizers in phase modulated transmission systems [C]// LEOS ’09: Proceedings of the 2009 Lasers & Electro-Optics Society Meeting Annual Meeting Conference. Piscataway, NJ: IEEE, 2009: 193-194.

[11] 谷源涛,唐昆,崔慧娟,等.新的变步长归一化最小均方算法[J].清华大学学报(自然科学版),2002,42(1):15-18. (GU Y T, TANG K, CUI H J, et al. A new variable step length normalized least mean square algorithm [J]. Journal of Tsinghua University (Science and Technology), 2002, 42(1): 15-18.)

[12] 罗小东,贾振红,王强.一种新的变步长LMS自适应滤波算法[J].电子学报,2006,34(6):1123-1126. (LUO X D, JIANG Z H, WANG Q. A new variable step size LMS adaptive filtering algorithm [J]. Acta Electronica Sinica, 2006, 34(6): 1123-1126.)

[13] 管四海,李智.基于修正反正切函数的变步长LMS算法[J].中国科技论文,2016,11(14). (GUAN S H, LI Z. A variable step size LMS algorithm based on modified arc tangent function [J]. China Sciencepaper, 2016, 11(14).)

[14] 王蒙,赵建平,张炳婷.一种基于双曲正割函数的变步长LMS算法[J].通信技术,2016,49(6):668-672. (WANG M, ZHAO J P, ZHANG B T. A variable step size LMS algorithm based on hyperbolic secant function [J]. Communications Technology, 2016,49(6):668-672.)

This work is partially supported by the National Natural Science Foundation of China (11374162), the Key Project of Natural Science in Colleges and Universities (TJ215009).

ZHENGYifeng, born in 1993, M. S. candidate. His research interests include circuits and systems.

HAOXueyuan, born in 1976, Ph. D., senior engineer. His research interests include signal processing.

YANXiaohong, born in 1963, Ph. D., professor. His research interests include physical electronics.

Newleastmeansquarealgorithmwithvariablestepbasedonunderwateracousticcommunication

ZHENG Yifeng*, HAO Xueyuan, YAN Xiaohong

(SchoolofElectronicScienceandEngineering,NanjingUniversityofPostsandTelecommunications,NanjingJiangsu210000,China)

In underwater acoustic communication, multipath effect channel can cause severe Inter-Symbol Interference (ISI). In view of the problems of the existing equalization algorithms when dealing with ISI, including slow convergence speed and huge steady-state error, as well as the complicated algorithm and being difficult to carry out hardware migration, a new variable step Least Mean Square (LMS) algorithm was proposed with anticosine step function and three adjustment parameters within the Feed-Forward Equalizer and Decision Feed-back Equalizer (FFE-DFE) structure. Firstly, simulations of three adjustment parameters includingα,β,rwere given to optimize the algorithm and compare it with traditional LMS algorithm, Modified Arctangent based Variable Step LMS (MA-VSLMS) and Hyperbolic Secant function based Variable Step size LMS algorithm (HS-VSLMS) in convergence and steady-state error. The simulation results showed that compared with the traditional LMS algorithm, the convergence speed of the proposed algorithm was 57.9% higher, and the steady-state error was reduced by 2 dB; compared with HS-VSLMS and MA-VSLMS, the convergence speed of the proposed algorithm was 26.3% and 15.8% higher, respectively, and the steady-state error was reduced by 1-2 dB. Finally, the proposed algorithm was transplanted to signal processing module and tested in an underwater experiment. Experimental results indicate that the signal is recovered very well after the equalizer, and the ISI problem caused by multipath effect is solved in the actual scene.

underwater acoustic communication; Inter-Symbol Interference (ISI); Least Mean Square (LMS) equalization algorithm; variable step function; decision feed-back equalizer

TP301.6

A

2017- 02- 10;

2017- 03- 17。

国家自然科学基金资助项目(11374162)；高校自然科学重点资助项目(TJ215009)。

郑奕丰(1993—)，男，江苏无锡人，硕士研究生，主要研究方向：电路与系统； 郝学元(1976—)，男，江苏南京人，高级工程师，博士，主要研究方向：信号处理； 颜晓红(1963—)，男，湖南衡阳人，教授，博士生导师，博士，主要研究方向：物理电子学。

1001- 9081(2017)08- 2195- 05

10.11772/j.issn.1001- 9081.2017.08.2195