基于遗传算法的CO2管道运输优化设计研究
2017-10-20刘佳佳范利军田群宏赵东亚李兆敏
刘佳佳,范利军,田群宏,赵东亚,李兆敏
1.中国石油大学(华东)化学工程学院,山东青岛 266580
2.中国石油大学(华东)石油工程学院,山东青岛 266580
基于遗传算法的CO2管道运输优化设计研究
刘佳佳1,范利军1,田群宏1,赵东亚1,李兆敏2
1.中国石油大学(华东)化学工程学院,山东青岛 266580
2.中国石油大学(华东)石油工程学院,山东青岛 266580
CO2捕集与封存(CCS)技术可分为捕集、运输和封存三个步骤。CO2运输作为CCS技术的中间环节,具有极其重要的地位。管道运输是长距离、大输量CO2运输最经济有效的方法。针对CO2管道输送过程,建立管输系统模型,采用遗传算法进行优化设计,使管输系统安全运行且费用最低。通过算例仿真讨论了不同质量流及管道长度条件下的优化结果,与现有优化方法相比,管输系统遗传算法优化方法适应力更强,证明了该方法的有效性。
CCS技术;管道运输;遗传算法;优化
温室效应引起的灾难性天气越来越引起各国关注,CO2作为主要温室气体的来源,需采取有效方法减少其排放量[1]。工业革命以后,人们对化石燃料的需求日益增大,CO2的最主要排放源就是化石燃料的燃烧,开发一种碳捕集封存方法成为减少CO2排放量的主要途径[2]。CCS(Carbon Capture and storage)技术是指将大型发电厂所产生的CO2收集起来,并且采用各种不同的方法进行储存以避免其被排放进入大气中的一种技术[2]。CCS技术是未来大规模减少CO2排放,缓解全球变暖的经济、可行的方法之一。CCS技术可以分为CO2的捕集、运输和封存三个步骤。CO2运输作为CCS技术的中间环节,具有极其重要的地位。与天然气、石油等的运输相似,对于长距离、大输量的CO2运输,最安全和经济的方法为管道运输[3]。合理配置管道入口压力、管道内径、管道壁厚、中间泵站数量,不仅能够为CO2的安全运输提供可靠保障,而且可以有效降低投资费用,因此,CO2管道运输优化设计是CCS技术应用的关键环节之一。本文主要研究内容是将遗传算法应用于CO2管道输送的优化设计中,通过算例仿真讨论不同质量流及管道长度下的优化结果,提出合理的方法来配置管道入口压力、壁厚、管道内径和中间泵站数量等参数,以达到管输系统满足安全要求且费用最少的目的。
1 遗传算法简介
遗传算法是通过模拟自然进化过程来搜索问题最优解的方法[4]。该算法是由一个代表问题可能的潜在解集种群开始,经过基因编码后,一定数目的个体组成了种群。种群中的每个个体实际上是带有染色体特征的实体。染色体的内部表现是某种基因组合,它直接决定了个体的外部表现。所以在开始时需要进行个体从表现型到基因型的编码工作。在实际应用遗传算法编码求解问题时,往往会对编码方法进行一些简化处理,如采用二进制编码方法。遗传算法的流程如图1 所示[5]。
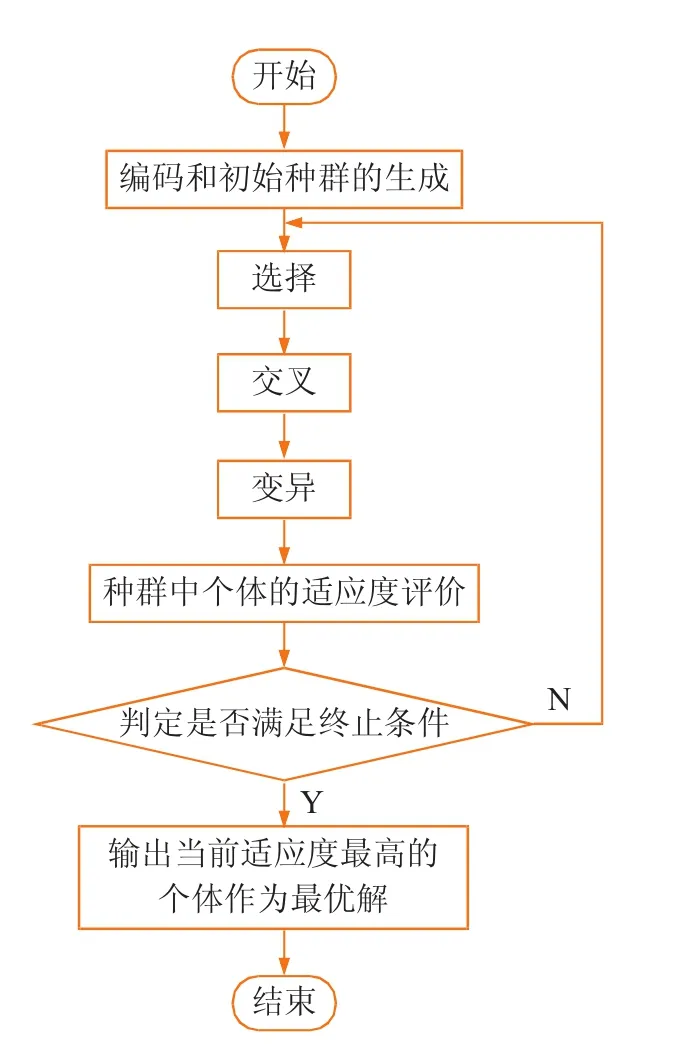
图1 遗传算法流程
2 CO2输送管道模型建立
2.1 简化分析假设条件
对于长距离CO2运输管道而言,整个运输系统由管道、泵站等组成。为了进行简化分析,在不影响结论的前提下,提出以下假设[6]:
(1)线路走向确定,线路附近地形起伏较小。
(2)每段管道的管径、壁厚等尺寸在段内相同。
(3)泵站等距布置,各个泵站使用的泵机组为同一型号。
2.2 管道关键模型建立
2.2.1 CO2管输系统管径模型
为便于进行优化设计,对现使用的优化模型进行改进。管道内径计算公式如下[7-8]:

式中:D为管道内径,mm;Qm为CO2质量流量,kg/s;ρ为CO2的密度,kg/m3;μ为CO2的黏度,Pa·s。
借鉴文献中提供的数据,应用最小二乘法进行参数辨识,获得CO2计算密度fρ(kg/m3)和计算黏度 fμ(Pa·s)的计算公式[7-8]:

式中:Aρ、Bρ、Aμ、Bμ为系数;Cρ、Cμ为常数。式(1)可转化为如下形式[7,8]:
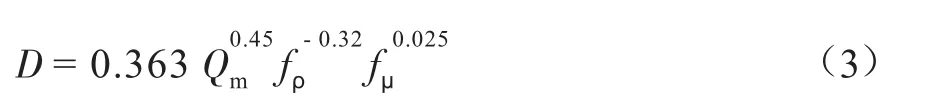
2.2.2 CO2管输系统管道费用模型
CO2输送管道的费用[9]包括管道的投资费用CIpi(元)和管道的运行维护费用Cpom(元):

式中:Cps为单位质量钢材的费用,元/kg;Wsteel为管道的质量,kg,Wsteel=0.024 66×d×103×(D+d)×103×L(d为管道壁厚,mm;L为管道长度,km);fm为材料费用因子;fpom为管道运行维护费用因子。
2.2.3 CO2管输系统泵站费用模型
泵站费用[9]包括压缩机站投资费用CIbo(元)、压缩机站运行与维护费用Cbom(元)和压缩机站用电费用CBE(元):

式中:fai为泵站备用因子;α为泵成本费因子;β为泵成本费因子;r为其他货币对人民币汇率;Wca为压缩机站装机容量,MW,Wca=Qm/ρ·(x-p1)/yi(p1为管道入口压力,MPa);n为压缩机站数量,个;Cpe为电费,元/(kw·h);fbom为泵运行维护费用占泵站投资费用百分比。
2.2.4 CO2管输系统中压缩系统费用模型
压缩系统总费用包括压缩系统投资费用[9]CIcomp(元)、压缩系统电费CCE(元)和压缩系统运行与维护费用Ccom(元):
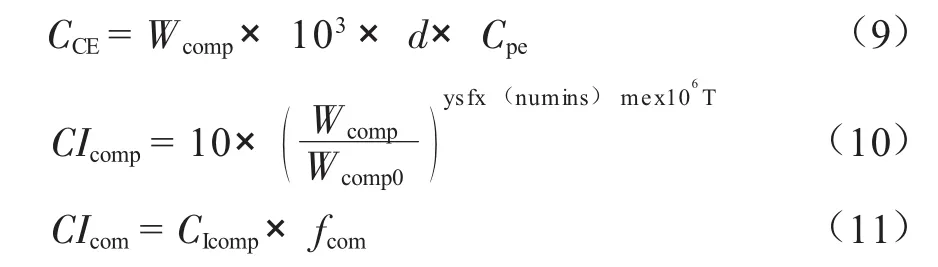
式中:Wcomp为压缩系统装机容量,MW;fcom为压缩系统运行与维护因子。
3 CO2管道优化模型求解及仿真
3.1 优化模型描述
在CO2管道优化设计中,一般都是针对某一固定的CO2捕集源进行管道输送,所以通常都是在确定的输量Qm条件下,通过优化管道系统参数取得最佳方案。根据第二部分建立的管道模型,结合流速约束、压力约束等约束条件,建立以费用作为目标函数的CO2输送管道优化模型:
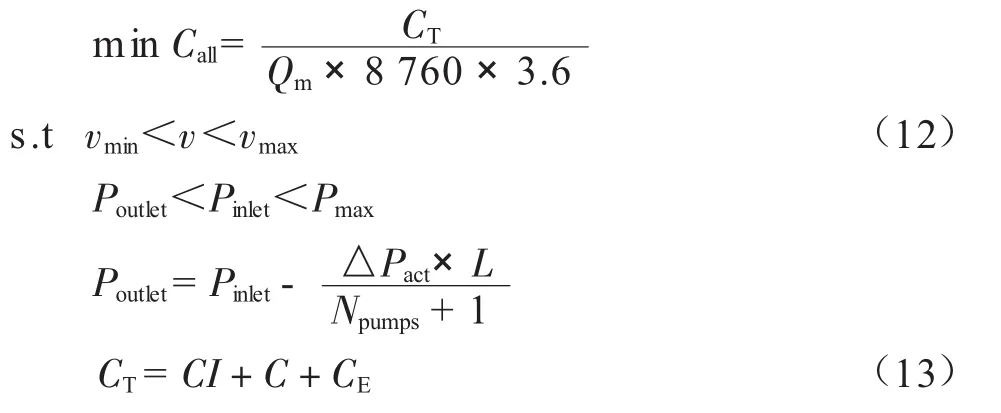
式中:Call为CO2输送管道的平准化费用,元/t;CT为管道投资、维护和动力费用,元。

式中:CRF1、CRF2为资本回收系数;CIbo为压缩机站投资费用,元;CIcomp为压缩系统投资费用,元;CIpipe为管道投资费用,元;C为各系统的运行维修费用之和,元;Cpom为管道运行维护费用,元;Cbom为压缩机站运行维护费用,元;Ccom为压缩系统运行维护费用,元;CE为压缩机站和压缩系统用电费用之和,元;CBE为压缩机站用电费用,元;CCE为压缩系统用电费用,元。
3.2 模型求解方法
针对上述CO2管输系统模型,采用遗传算法编制相关程序进行仿真求解。遗传算法求解问题的具体步骤如下。
3.2.1 遗传算法中初始群体的产生
初始群体由随机产生的N个随机个体组成,每个个体是由各个管道入口压力按照一定顺序连接在一起的字符串,因此,不同的个体代表了不同的管道入口压力选择情况。
3.2.2 遗传算法中适应度评价标准
可通过计算个体的适应度来评价个体的优劣性。将式(3)、(4)、(6)~(11)代入式(12),选择管道平准化费用Call为评价函数。以群体中各个个体的适应度作为依据,经过反复迭代,不断寻求其中适应度较大的个体,最终得到管道优化设计问题的最优解。
3.2.3 遗传算法中选择运算
选择是在对个体的Call评价的基础上进行的操作。在优化的过程中,选择运算的原则是,根据得到较小数值的Call,找出相应的个体并以较高的概率遗传到下一代,而根据数值较大的Call,找出相应个体,并以较低概率遗传到下一代,通过该方式对群体中的个体进行优胜劣汰操作。
3.2.4 遗传算法中交叉与变异运算
遗传算法的局部和全局搜索能力对管道优化解的质量至关重要。以管道入口压力代表种群个体,对搜索空间同时进行局部搜索和全局搜索,将交叉算子与变异算子相互配合共同使用,使得遗传算法能够以良好的搜索性能完成管道优化问题的寻优过程。
根据以上的步骤,基于遗传算法对管道进行优化设计,优化的参数包括半径、壁厚、入口压力、泵站数量。根据优化得到的管径参数,结合标称管径进行内径和壁厚的选择,得到工程实际中可直接使用的管道优化结果。
3.3 仿真和结果分析
根据建立的CO2管道系统优化模型,采用遗传算法搜索最优解。为验证算法的有效性,现对CO2输送管道进行优化设计。
模型中管道运输系统基本参数如表1~3所示:

表1 管道运输系统基本参数[10-12]

表2 管道参数[13-14]

表3 泵站和压缩机参数[9,15]
不同管道输送质量流量下的管道参数计算结果如表4所示。
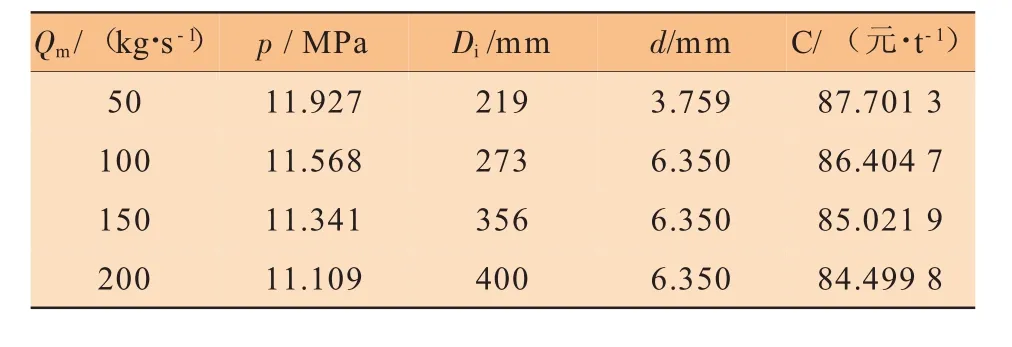
表4 不同质量流量下管道参数优化结果
从表4中可以看出通过优化入口压力、管径、壁厚等管道参数可得到最优的平准化费用,相应关系如图2所示。
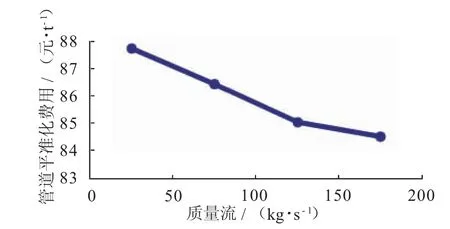
图2 不同质量流量下优化管道费用
提出的优化方法可有效进行管道优化设计,例如:Qm=50 kg/s时,优化入口压力P1为11.927 MPa,管道直径Di为219 mm,壁厚d为3.759 mm,平准化费用C为87.701 3元/t。
不同管道长度下管道的平准化费用如图3所示。

图3 不同管道长度下平准化费用
从图3可以看出,管道的平准化费用随着长度增大而呈非线性增大的趋势。
4 结论
管道运输是大规模、长距离输送CO2经济有效的方式。针对管道输送设计需达到技术上可靠且经济上合理的要求,在建立管道优化模型的基础上,运用遗传算法进行参数优化设计,结合管道公称尺寸表进行管道内径和壁厚的优化选择。结果表明:提出的优化方法不仅可以满足设计的要求,而且能够有效地降低管道运输的平准化费用。CO2输送管道优化是在复杂多约束条件下决策类优化问题,未来还需综合考虑社会、经济、环境等多种约束因素,以满足工程实际要求。
[1]赵青,李玉星,李顺丽.超临界二氧化碳管道杂质对节流温降的影响[J].石油学报,2016,37(1):111-115.
[2]朱义成.二氧化碳吸附分离过程数值模拟与优化[D].济南:山东建筑大学,2010.
[3]叶健,杨精伟.液态二氧化碳输送管道的设计要点[J].油气田地面工程,2010,29(4):37-38.
[4]崔佳.遗传算法在神经模糊控制器优化和BP神经网络优化中的应用[D].郑州:郑州大学,2007.
[5]梁潇.基于遗传算法的油气管道线路优化研究[D].成都:西南石油大学,2015.
[6]李科星.微粒群算法在热油管道优化设计中的应用研究[D].成都:西南石油学院,2005.
[7]田群宏,赵东亚,李兆敏,等.CO2管道运输系统鲁棒优化设计[J].大连理工大学学报,2016(1):98-102.
[8]ZHAO D,TIAN Q,LI Z,et al.A new stepwise and piecewise optimization approach for CO2pipeline[J].International Journal of Greenhouse Gas Control,2016,49:192-200.
[9]KNOOPE M M J,GUIJT W,RAMírez A,et al.Improved cost models for optimizing CO2,pipeline configuration for point-to-point pipelines and simple networks[J].International Journalof Greenhouse Gas Control,2014,22(2):25-46.
[10]GAOL,FANGM,LIH,etal.Costanalysis of CO2transportation:Case study in China[J].Energy Procedia,2011,4(22):5 974-5 981.
[11]ZHANG Dongjie,WANG Zhe,SUN Jining,et al.Economic evaluation of CO2pipeline transport in China [J].Energy Conversion and Management,2012,55:127-135.
[12]CHANDEL M K,PRATSON L F,WILLIAMS E.Potential economies of scale in CO2,transport through use of a trunk pipeline[J].Energy Conversion and Management,2010,51(12):2 825-2 834.
[13]SEAN T MCCOY,EDWARD S RUBIN.An engineering economic model of pipeline transport of CO2with application carbon capture and storage[J].International Journal of Greenhouse Gas Control,2008,2(2):219-229.
[14]VANDEGINSTEV,PIESSENS K.Pipelinedesignfora least-cost router application for CO2, transport in the CO2,sequestration cycle[J].International Journal of Greenhouse Gas Control,2008,2(4):571-581.
[15]ZHANG Z X,WANG G X,MASSAROTTO P,et al.Optimization of pipeline transport for CO2,sequestration[J].Energy Con version and Management,2006,47(6):702-715.
Optimization design ofCO2pipeline transportation based on genetic algorithm
LIU Jiajia1,FAN Lijun1,TIAN Qunhong1,ZHAO Dongya1,LIZhaomin2
1.College of ChemicalEngineering,China University of Petroleum,Qingdao 266580,China
2.College of Petroleum Engineering,China University of Petroleum,Qingdao 266580,China
Carbon capture and storage (CCS)technology can be divided into three stages:capture,transport and storage.Carbon transport is the middle stage of CCS technology,which has a very important position in CCS.For long distance and large volume of CO2transport,the most secure and economical method is pipeline transportation.The model of pipeline transportation system is established in the pipeline design.A genetic algorithm is presented to optimize the design of CO2pipeline transportation process,which makes the pipeline transportation system operation with safety and minimum cost.Based on the simulation example,the optimization results under different mass flow and pipeline length are discussed.Compared with the existing optimization methods,the genetic algorithm optimization method is more adaptable,which proves the effectiveness of the proposed method.
CCS technology;pipeline transport;genetic algorithm,optimization
10.3969/j.issn.1001-2206.2017.05.003
国家自然科学基金(61473312;61273188);国家科技重大专项(2016ZX05012002-004);中央高校基本科研业务费专项资金(15CX06053A)资助。
刘佳佳(1994-),女,宁夏银川人,中国石油大学(华东)化学工程学院在读硕士研究生,主要从事管道运输、化工过程建模与优化的研究。Email:dyzhao@upc.edu.cn
2017-03-21;
2017-06-12
