指数波形松弛方法

(闽江学院 数学系,福建 福州 350108)

指数波形松弛方法

范振成

(闽江学院 数学系,福建 福州 350108)

结合常微分方程的指数方法和波形松弛方法,建立指数波形松弛方法。然后证明了该方法是收敛的。最后通过算例与显式欧拉方法、指数方法和波形松弛方法进行对比。结果表明，对于弱耦合的大系统,指数波形松弛方法具有一定优势。

刚性微分方程;指数方法;波形松弛方法

刚性方程是一类重要的常微分方程[1]。大多数刚性方程没有解析解，建立数值方法求近似解是必要的。常微分方程的数值方法可以分为显式和隐式两类。大量理论研究和实际应用表明:显式方法不适合刚性方程，一般用隐式方法求解[2]。然而，隐式方法将导致非线性方程组，求解非线性方程组(尤其大方程组)是一个艰巨的任务。指数方法先通过指数型变换弱化系统的刚性，进而可以用显式方法达到较理想的计算结果[3-4]。而当系统规模太大时，前述3种办法都可能超出容许度。波形松弛方法是为了求解大系统而建立的，它具有并行性和多速率性两个优点，适用于由一些子系统弱耦合而成的大系统[5-6]。

对于大的刚性系统，单独的指数方法和波形松弛方法都不理想，前者不适用大系统，后者难以处理刚性问题。本文的指数波形松弛方法将两种方法结合，利用波形松弛方法分解计算，利用指数方法弱化刚性，兼具两种方法的优点。

1 指数波形松弛方法

考虑刚性初值问题:

这里要求g(t，x(t))具有小Lipschitz常数，线性部分Ax一般通过对f(t，x(t))线性化获得。

建立波形松弛方法

上式最后一个方程两边同乘e-At得

进而有

令T>0,取[0,T]上步长为h的等距节点集{t0,t1,…,tN},其中,

t0=0,tN=T,h=T/N,ti+1=ti+h,i=0,1,…,N-1。

式(1)两端从tn到tn+l积分得

用Newton-Cotes公式近似上式中的定积分(见文献[7])

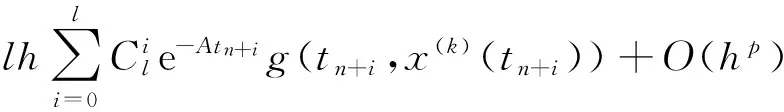
2 收敛性证明

引理[7]：设{cj}为实数列,满足

cj+1≤ajcj+bj,j=0,1,…,m-1

其中,aj>0,bj∈R,则cj≤Ej(j=0,1,…,m),其中,

定理：假设函数g满足Lipschitz条件,即存在L使得对所有x1,x2∈R

|g(t,x1)-g(t,x2)|≤L|x1-x2| (4)

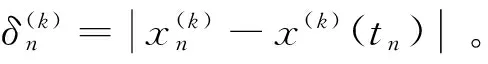
那么

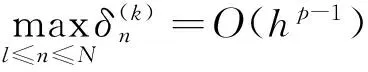
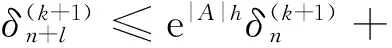
由式(4)、(5)和归纳假设有

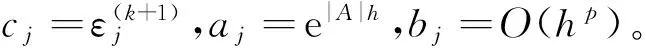
由引理得

3 数值实验

通过数值实验对比指数波形松弛方法与3种传统方法: 显式欧拉方法、指数方法、波形松弛方法。为简单使用线性实验方程,并且所有方法都基于显式欧拉方法。

考虑初值问题

此方程解的第一分量变化快,其余3个分量变化慢,这是刚性方程。记

使用分割f(t,x)=Ax+g(t,x)=Ax+Bx.取步长h=0.001,N=0.1/h=100,x0=x(0)。方程(8)的显式欧拉方法为

基于显式欧拉方法的指数方法、波形松弛方法和指数波形松弛方法分别为

表1 在t=0.1处方程(8)的精确解的值和数值方法(9)～(12)的计算值Tab.1 The value of the exact solution and approximate solutions generated by(9)～(12)at t=0.1 for equation(8)

方法(9)～(12)都是显式方法,一般情况显式方法不能用来求解刚性问题。从表1中数据可以看出显式欧拉方法(9)、波形松弛方法(11)的计算结果误差较大,而同样步长的指数波形松弛方法(12)和指数方法(10)计算结果较准确,说明建立的指数波形松弛方法一定程度上克服了显式方法的缺点,可以用于求解刚性方程。方法(12)需要迭代3次,计算量比方法(10)大,但方法(12)继承了波形松弛方法的优点,即通过选择适当的分割函数(比如块对角矩阵),可以将计算任务分解成若干独立的小任务,进而在不同的处理器上同时完成,而且允许在不同处理器上使用不同方法,因而比方法(10)更适合弱耦合的大系统。

[1] 袁兆鼎,费景高,刘德贵.刚性常微分方程初值问题的数值解法[M].北京：科学出版社,1987.

[2] Dekker K,Verwer J G.Stability of Runge-Kutta methods for stiff nonlinear differential equatons[M].Amsterdam:Elsevier Science Ltd,1984.

[3] Hochbruck M,Ostermann A.Exponential multistep methods of Adams-type[J].Numerical Mathematics,2011,51(4):889-908.

[4] Xu Y,Zhao J J,Sui Z N.Exponential Runge-Kutta methods for delay differential equations[J].Mathematics and Computers in Simulation,2010,80(12):2350-2361.

[5] Hout K J.On the convergence of waveform relaxation methods for stiff nonlinear ordinary differential equations[J].Applied Numerical Mathematics,1995,18(1):175-190.

[6] Zhou S,Huang T Z.Convergence of waveform relaxation methods for Hermitian positive definite linear systems[J].Applied Mathematics and Computation,2008,203(2):943-952.

[7] 张平文,李铁军.数值分析[M].北京:北京大学出版社,2007.

(责任编辑：陈雯)

Exponentialwaveformrelaxationmethods

Fan Zhencheng

(Mathematics Department,Minjiang University,Fuzhou 350108，China)

Firstly,the exponential waveform relaxation methods (EWRMs) for ordinary differential equations are established by combining the exponential methods (EMs) and the waveform relaxation methods (WRMs).Secondly,the convergence of the EWRMs is confirmed.Lastly,numerical experimentation is conducted to make a comparison among the explicit Euler methods,EMs and WRMs.The results indicate that the EWRMs are advantageous for large weakly coupled systems of ordinary differential equations.

stiff differential equation;exponential method;waveform relaxation method

O241.81

A

1672-4348(2017)04-0364-03

10.3969/j.issn.1672-4348.2017.04.011

2017-03-14

福建省自然科学基金(2015J01588);福建省设区市属高校科研专项(JK2014041)

范振成(1971-),男,黑龙江依安人,教授,博士，研究方向：随机微分方程数值方法。