堤防建设中防渗墙对地下水环境影响分析
2017-10-18董丁硕张志辉
赵 峰,董丁硕,张志辉
(1.松辽水环境科学研究所,吉林长春130021;2.合肥工业大学,安徽合肥230019;3.长春黄金设计院,吉林长春130012)
堤防建设中防渗墙对地下水环境影响分析
赵 峰1,董丁硕2,张志辉3
(1.松辽水环境科学研究所,吉林长春130021;2.合肥工业大学,安徽合肥230019;3.长春黄金设计院,吉林长春130012)
本文以吉林省段松花江干流治理工程的九台红旗大堵截下段堤防段为垂直防渗的典型堤段剖面进行地下水流场二维数值模拟,对比有无截渗墙时地下水流场特征,讨论截渗墙对地下水运动的影响。这样可以直观、准确地得到截渗墙对地下水环境的影响作用大小,可直观分析堤防建设对地下水的影响程度,为工程决策提供依据。
地下水;环境影响;二维概念模型;防渗墙;数值模拟
截渗墙主要是用来处理堤防工程中存在的渗流问题,它的实施不仅能有效改善堤身和堤基的渗流状态,对地下水流场影响明显,通过选取实施垂直防渗的典型堤段剖面进行地下水流场二维数值模拟,对比有无截渗墙时地下水流场特征,讨论截渗墙对地下水运动的影响,可以直观、准确地得到截渗墙对地下水环境的影响程度。
1 工程概况
吉林省段松花江干流治理工程项目分布于松花江两岸,设计堤防护坡工程65处,堤防护坡防渗工程42处,从上游到下游典型防渗段有红旗大堵截段、张家坨子堤防段、平底泡堤段、泔水缸堤防段。数值模拟反映的趋势基本一致,此次以九台红旗大堵截下段堤防段为例进行讨论。
典型堤段水泥土垂直防渗墙示意图见图1。

图1 水泥土垂直防渗墙示意图
2 地下水数值模拟
2.1 水文地质概念模型
九台红旗大堵截下段堤防段地表包气带岩性主要为亚粘土,往下为粗砂含水层、砾石含水层,含水层较厚,再往下为亚粘土隔水层。此次剖面模拟通过渗透系数控制不同含水层在水平方向和垂直方向上的渗透性,将剖面概化为均质各向异性含水层。工程区地下水流的天然水力梯度很小,在水平方向上流动相对比较缓慢,渗流基本符合达西定律,地下水流形式可以概化为剖面二维流。
2.2 数学模型及求解方法
根据水文地质概念模型及边界条件,建立均质各向异性二维稳定流数学模型来模拟剖面地下水流特征。

式中:Ω——剖面渗流区域;h——含水层水位标高,m;Kx,Kz分别为水平方向和垂向上的渗透系数,m/d;w——源汇项,m/d;h1——水头边界上水头分布,m;T——含水层导水系数,m/d;B1——水头边界;B2——流量边界;q(x ,z)——流量边界单宽流量,m/d,流入为正,流出为负,隔水边界为0(流线边界视为零流量边界)。
此次模拟采用GMS软件对地下水流数值模型求解。GMS的MODFLOW模块采用有限差分法对数学模型进行离散,对于数据的插值计算一般采用克里金法,模型求解一般采用PCG2法。
2.3 模型建立
2.3.1 模型离散
根据典型堤段剖面模拟范围,及堤坝和防渗墙设计标准,此次建模网格大小剖分为2 m×1 m,共13 780个,其中参与模拟的网格共13 251个。
2.3.2 水文地质参数初值
含水层及弱透水层的渗透性通过不同单元格的渗透系数来控制。剖面地层岩性主要是亚粘土,根据当地抽水试验及经验值进行赋值;堤防及水泥土垂直防渗墙渗透系数根据设计值进行赋值,见表1。

表1 红旗大堵截堤段剖面渗透系数表
2.3.3 初始水头设置
松花江为一类水头边界,由于江水主要在汛期补给地下水,采用设计洪水位作为计算边界水位;枯水期采用计算水平年枯水期水位作为边界水位。
2.3.4 源汇项设置
此次工作主要模拟汛期江水对地下水的补给,向两侧径流途中降水补给和蒸发排泄基本可以忽略;在剖面边缘为侧向流出边界,根据水力坡度计算侧向流出量并赋值。
2.4 模拟结果及分析
丰水期、枯水期九台红旗大堵截下段堤防段防渗前后,有无垂直防渗墙模拟地下水位对比结果见表2。丰水期、枯水期红旗大堵截堤段进行垂直防渗后地下水流场见图1。
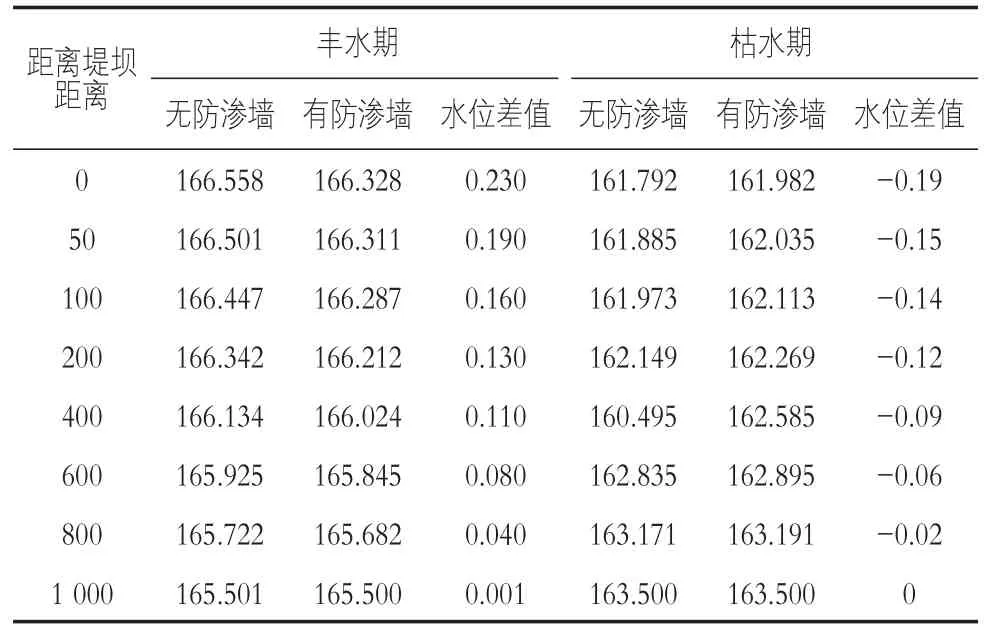
表2 红旗大堵截堤段剖面防渗前后地下水位对比表m
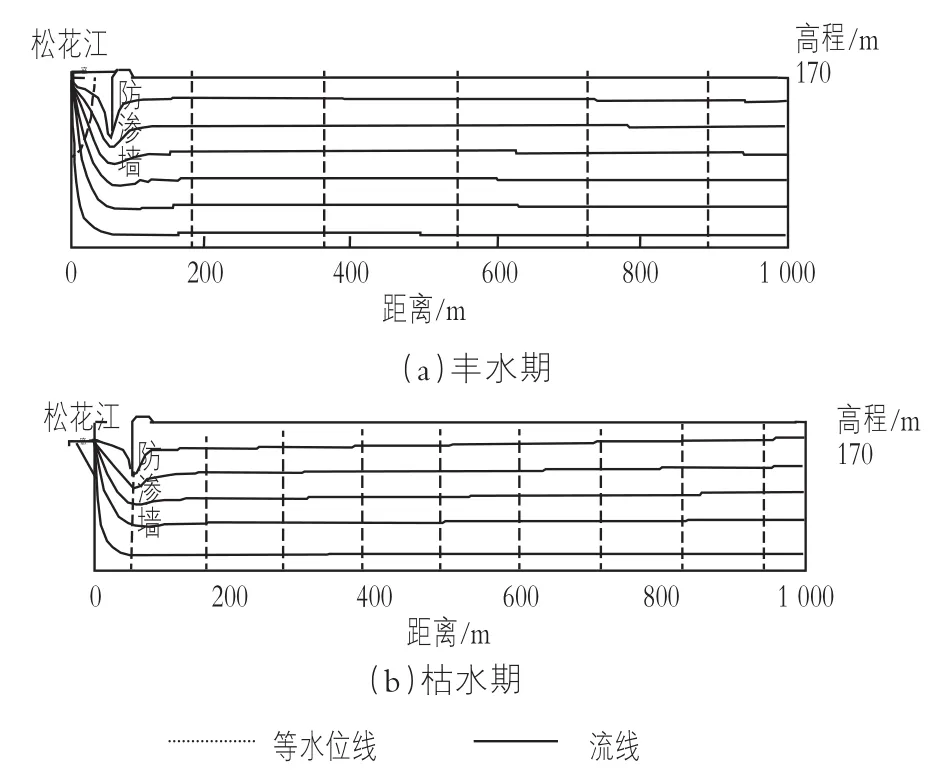
图1 红旗大堵截段剖面防渗后地下水流场特征图
3 结果分析
从图1可以看出,修建垂直防渗墙后,在丰、枯水期均出现明显的垂向绕渗现象,对地下水流场影响明显,但对地下水位影响不大。枯水期阻水侧产生一定的水位雍高,但水位变化较小。根据模型计算结果,在同一位置,阻水侧防渗后地下水位略高于没有修建防渗墙时的地下水位,防渗后最大雍高值为19 cm;当距离为200 m时,防渗后水位雍高值为12 cm左右,随着与防渗墙距离的增加,影响逐渐减小,当距离为600 m时,水位雍高值仅为6 cm左右,产生的影响很小。因此,防渗墙对地下水流场有一定的影响,枯水期垂直防渗墙有减缓地下水补给江水的作用,但对地下水位影响相对较小。
TV223.4+2
B
1002—0624(2017)10—0026—02
2017-07-04
